基于领航跟随的多机器人编队控制方法

高继勋，黄全振，赵媛媛

（1.河南工程学院计算机学院，河南 郑州 451191; 2.河南工程学院电气信息学院，河南 郑州 451191;3.郑州工程技术学院，河南 郑州450044）

0 引 言

随着人工智能时代的到来，多机器人的控制已逐渐成为研究热点[1-6]，其应用场景包括但不限于农业、军事、航空等领域。在多机器人编队的协同控制过程中，通常所期望队形是可变的，以便于应对单个机器人无法完成的复杂任务。在极坐标下，利用线性反馈的方法建立“距离-角度”控制器模型，完成对多机器人编队控制[7]。由于奇异点存在，该控制器存在一定问题。可通过将极坐标投影到笛卡尔坐标系下，重新建立控制模型解决奇异点问题[8-9]。钟宜生等[10]提出，将多机器人可变编队问题描述为“不变的队形在可变的坐标系中运动”的编队控制问题。在上述基础上，李清东[11]提出用多个不变队形互相切换，以完成编队控制。刘磊[12]采用以差速轮式机器人为研究对象，通过仿真验证该控制方法的可行性。

目前对于解决多机器人一般性编队控制问题，公开文献中尚未见到成熟方案。现阶段主要有人工势场法[13]、基于行为法[14]、虚拟结构法[15]和领航-跟随法[16]。上述方法各有其优缺点，相比较而言，领航-跟随法的控制更简单，只需调整跟随者与领航者的运动参数即可完成跟踪控制，具有较好的稳定性和灵活性[17-20]。

根据上述情况，本文提出了一种新颖的机器人编队控制方法，该方法基于领航-跟随法，引入“虚拟领航机器人”，将其他机器人作为跟随者，建立控制模型，从而将编队问题转化为跟踪控制问题。根据提出的控制算法，本文设计了跟随误差控制器，分析跟随误差及其收敛性。通过仿真与实验结果分析，验证本文提出的改进型领航-跟随控制方法在一致性控制中的有效性与稳定性。

1 问题描述和模型构建

1.1 问题描述

基于领航-跟随法，可将编队问题转化为跟随机器人对虚拟领航机器人的轨迹跟踪，该方法只需获得虚拟领航者的运动参数和位姿即可实现跟踪控制，一定程度上减少相互之间信息冗余及计算量。通过上述方法，建立虚拟领航机器人与跟随机器人运动模型，如图1所示。

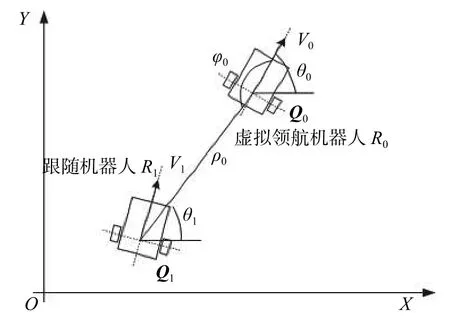
图1 领航-跟随结构示意图

图中，跟随机器人R1与虚拟领航机器人R0的距离是ρ0，二者中心线连线与虚拟领航机器人R0轴心线的夹角是φ0。通过虚拟领航者的引入，将编队控制转化为跟随移动机器人R1对虚拟领航机器人R0的轨迹跟踪，即跟随机器人R1在一定时间内跟随虚拟领航机器人R0运动就可组成相应的编队。

1.2 模型构建

非完整移动机器人的运动学模型[15]如下式：

由图1可知，当跟随机器人R1与虚拟领航机器人R0之间的位姿（位置和姿态）误差趋近于零，即：

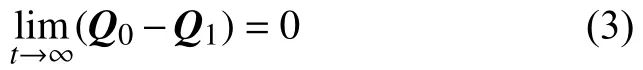
假设在t时刻，虚拟领航机器人与期望轨迹运动示意图如图2所示。

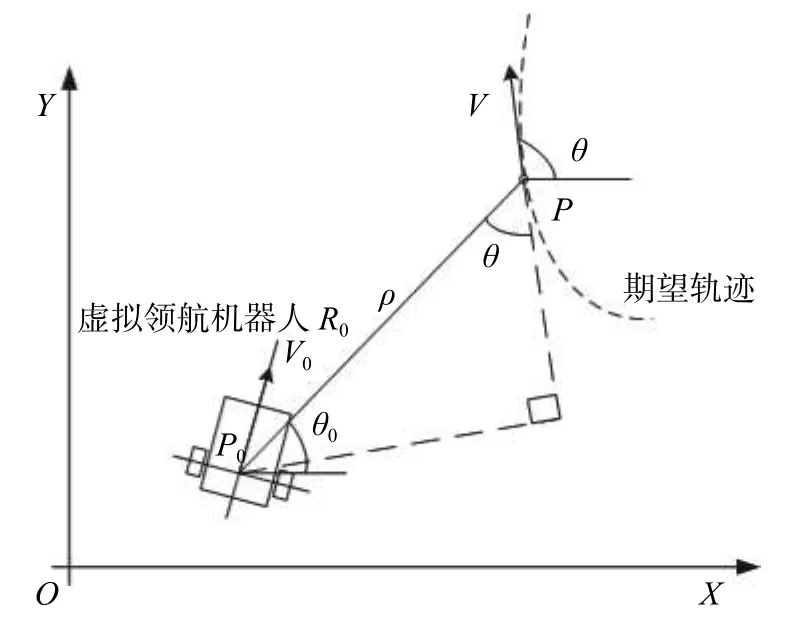
图2 跟踪位置示意图

其中，V为期望轨迹上P点的运动方向，与X轴正方向夹角为θ。P0P为虚拟领航机器人与期望轨迹上P点的连线。P点状态表示为（X,Y,θ）。

虚拟领航机器人与期望轨迹误差参数表示为：

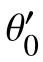
通过对参数λ的调整，可完成跟随机器人相对于期望轨迹的控制。

虚拟领航机器人运动学模型可表示为：

跟随机器人参考轨迹模型为：

根据期望轨迹P点状态及公式（4）可得到虚拟领航机器人位姿，其数学表达式如下：

2 控制器设计

跟随机器人R1与虚拟领航机器人R0位姿误差为ei，则ei可表示为：

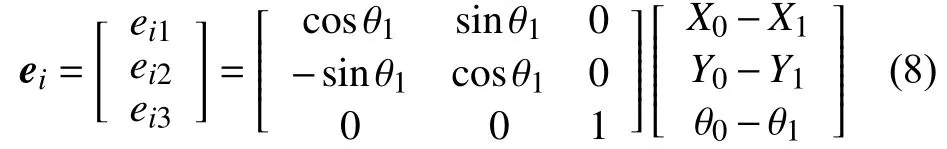
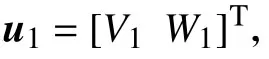
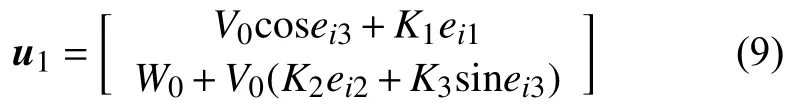
其中，K1，K2，K3为正数。

定义Lyapunov函数VL为：

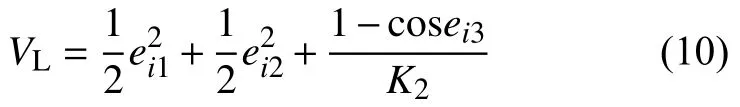
以上构建了基于领航跟随运动控制方法的控制器，并且证明了该控制器的稳定性。下面对该方法进行仿真与实验研究。

3 仿真分析与实验验证

为验证系统及控制算法的正确性和有效性，利用仿真软件和硬件平台构建模拟/物理实验系统进行验证。仿真采取与期望轨迹重合（追踪）、与期望轨迹保持固定队形（编队）两种情况进行，便于在不同控制场景下对结果分析。

3.1 仿真分析

仿真研究基于Gazebo机器人仿真软件构建的运动学与控制仿真平台。仿真固定参数以实际硬件平台为参考，其固定参数值如表1所示。

表1 仿真基本参数

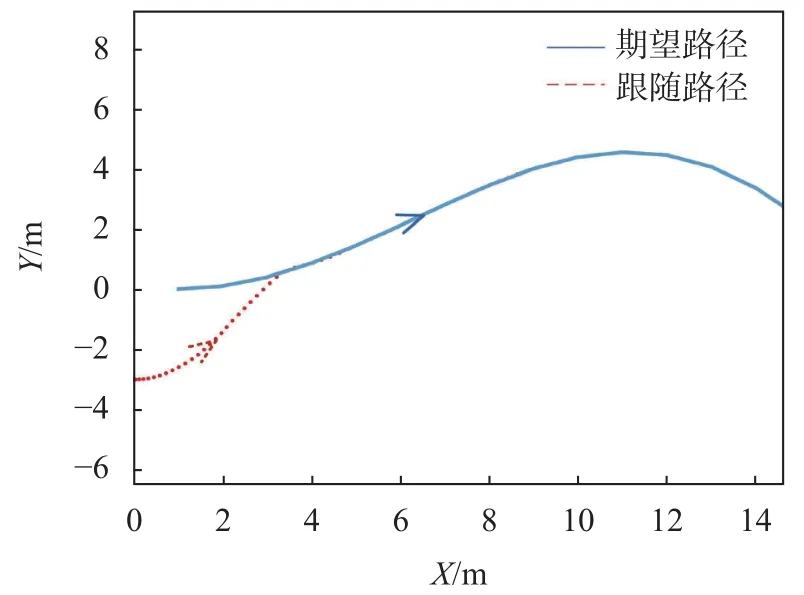
图3 λ=[0 0]T跟随机器人仿真运动轨迹

跟随机器人从任意初始位置开始运动，速度变化曲线如图4中虚线所示。由图可以看出，时间T从5 s左右速度开始变化，随后减小；从20 s左右开始，跟随机器人速度趋于稳定；30 s时，跟随机器人速度稳定在 0.8 m/s。

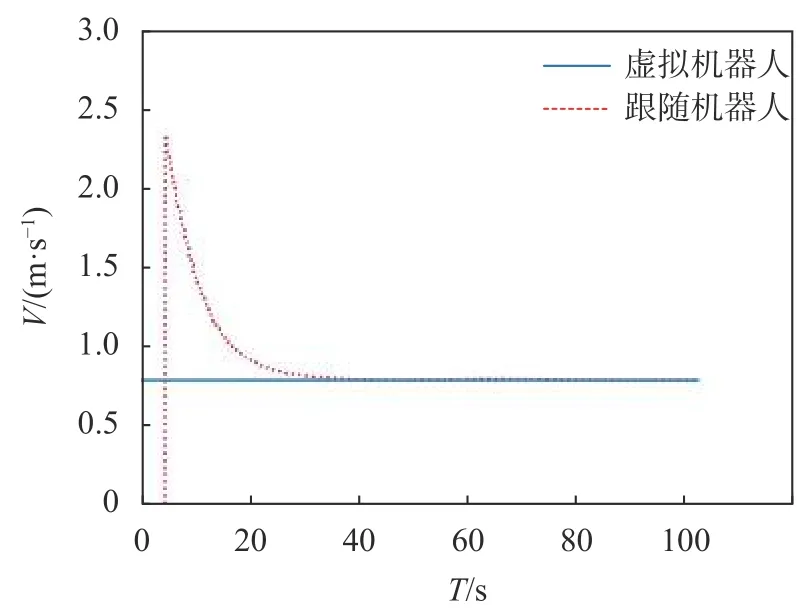
图4 λ=[0 0]T跟随机器人仿真速度曲线

设定虚拟领航机器人与期望路径距离为0.5 m，与速度方向夹角为π/6，即λ=[0.5 π/6]T。假设虚拟领航机器人速度为0.8 m/s，角速度为16 rad/s。即在某时刻，虚拟领航机器人中心线与期望轨迹连线长度为0.5 m，与期望轨迹该点切线方向夹角为π/6。跟随机器人运动轨迹如图5所示，其中，X、Y为机器人所处平面坐标，三角形为期望结构，端点为运动轨迹与虚拟机器人期望位置。

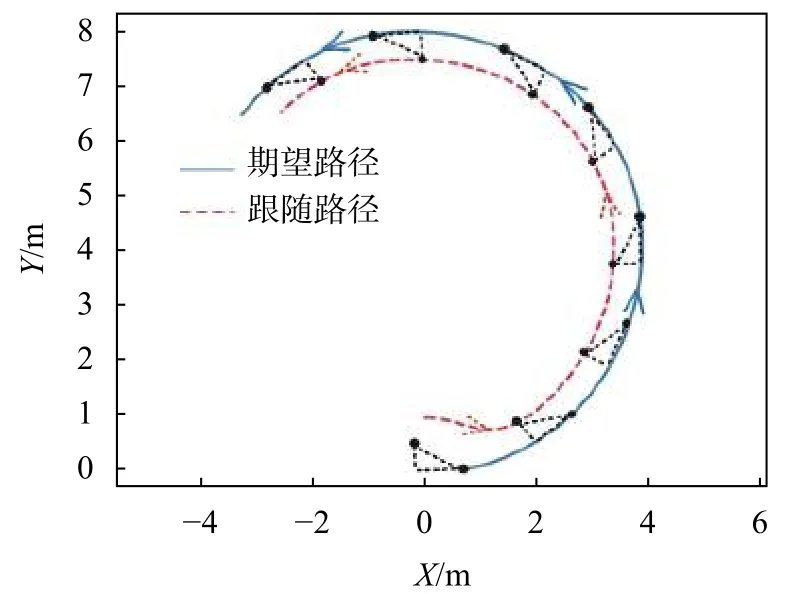
图5 λ=[0.5 π/6]T跟随机器人仿真运动轨迹

跟随机器人速度变化曲线如图6中虚线所示。当时间T从25 s开始，跟随机器人速度趋于稳定；40 s时，跟随机器人速度稳定在0.8 m/s。

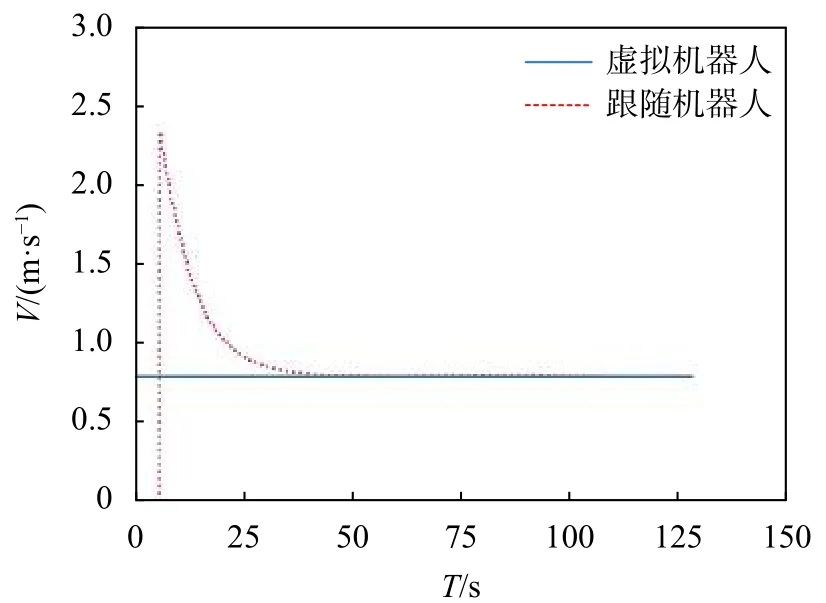
图6 λ=[0.5 π/6]T跟随机器人仿真速度曲线

3.2 实验验证

为移动机器人控制构建物理实验系统。该实验系统的硬件部分主要由双轮差速驱动底盘、IMU模块、差分GPS定位模块（RTK）和主计算机（Raspberry Pi4B）组成。

主计算机主要通过传感器模块采集到的数据进行运动状态计算，并且通过输出控制指令完成对底盘的运动控制；底盘执行主计算机的控制指令，按照控制指令完成运动；IMU模块为九轴惯性测量模块，用于测量机器人的运动状态，包括加速度和航向角等；差分GPS定位模块实现机器人的实时定位功能，具体实现为：将差分GPS移动接收端安装于机器人的底盘上，通过接收卫星与基准站数据进行差分计算，从而提高机器人的定位精度。

实验平台示意图及实物图如图7、图8所示。

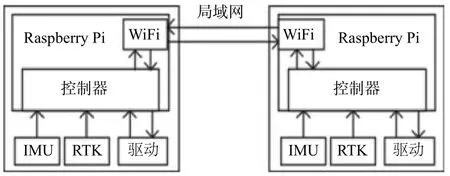
图7 实验平台示意图

图8 实验平台实物图

程序流程如图9所示。首先对跟随机器人进行状态初始化；然后根据GPS和IMU回传数据计算，并于期望位姿做姿态解算；通过结算结果，得到控制输入参数；最后输出给控制单元，并实时对跟随机器人状态进行监测，判断其是否达到预期位姿。

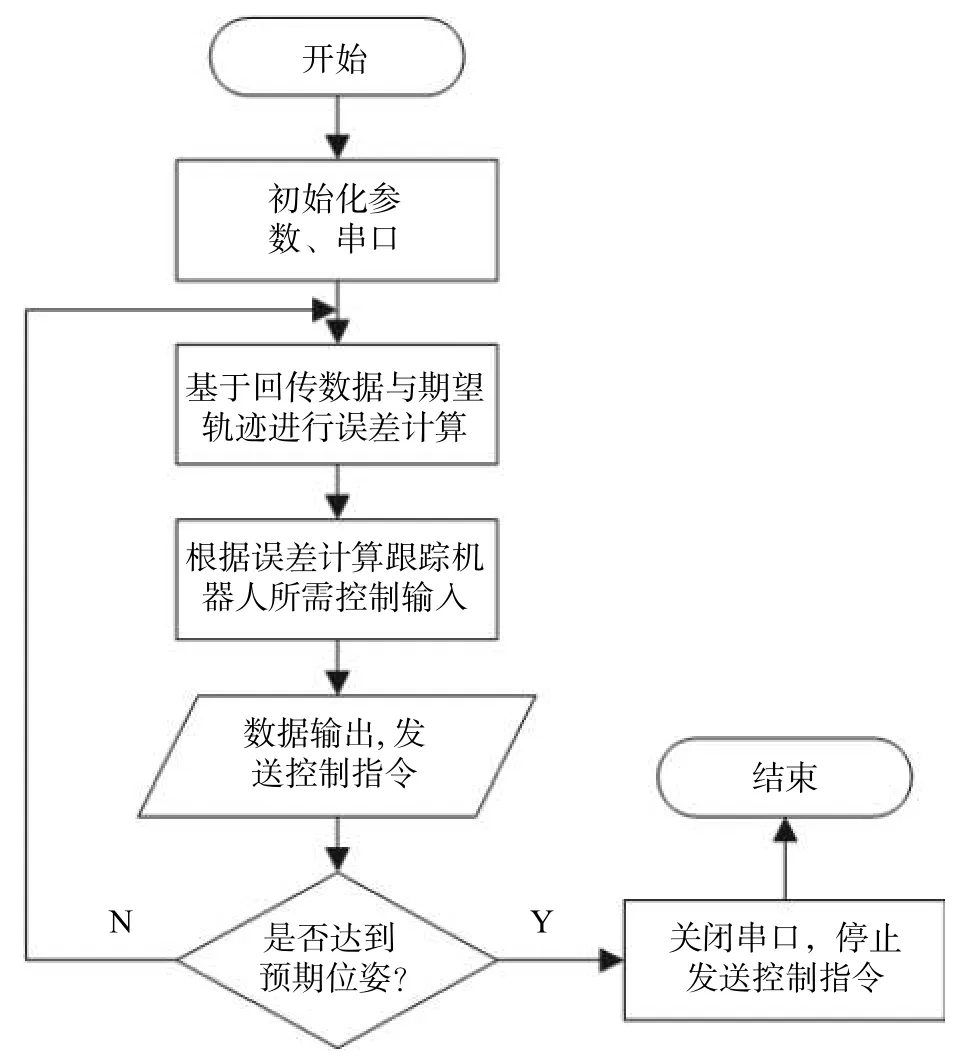
图9 跟随机器人控制实验流程图

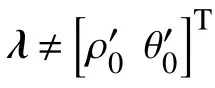
根据预设期望轨迹与虚拟领航机器人的当前位姿误差，计算跟随机器人所需控制输入参数，然后通过串口将运动控制指令发送给运动底盘。如此循环。

设定虚拟领航机器人与期望轨迹重合，即λ=[0 0]T。假设任意初始位置，虚拟领航机器人以速度为0.8 m/s，角速度为0匀速运动。跟随机器人运动轨迹如图10所示。其中，X、Y为机器人所处二维平面。

图10 λ=[0 0]T跟随机器人实验运动轨迹

跟随机器人速度变化曲线如图11中虚线所示。当时间T从20 s开始，跟随机器人速度趋于稳定；35 s时，跟随机器人速度稳定在0.8 m/s。

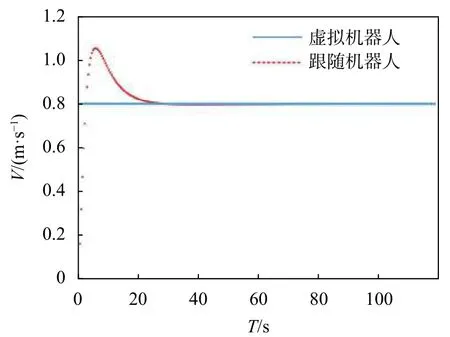
图11 λ=[0 0]T跟随机器人实验速度曲线

设定虚拟领航机器人与期望路径距离为0.5 m，与速度方向夹角为π/6，即λ=[0.5 π/6]T。假设虚拟领航机器人速度为0.8 m/s，角速度为16 rad/s。即在某时刻，虚拟领航机器人中心线与期望轨迹连线长度为0.5 m，与期望轨迹该点切线方向夹角为π/6。跟随机器人运动轨迹如图12所示，其中，X、Y为机器人所处平面坐标，三角形为期望结构，端点为运动轨迹与虚拟机器人期望位置。

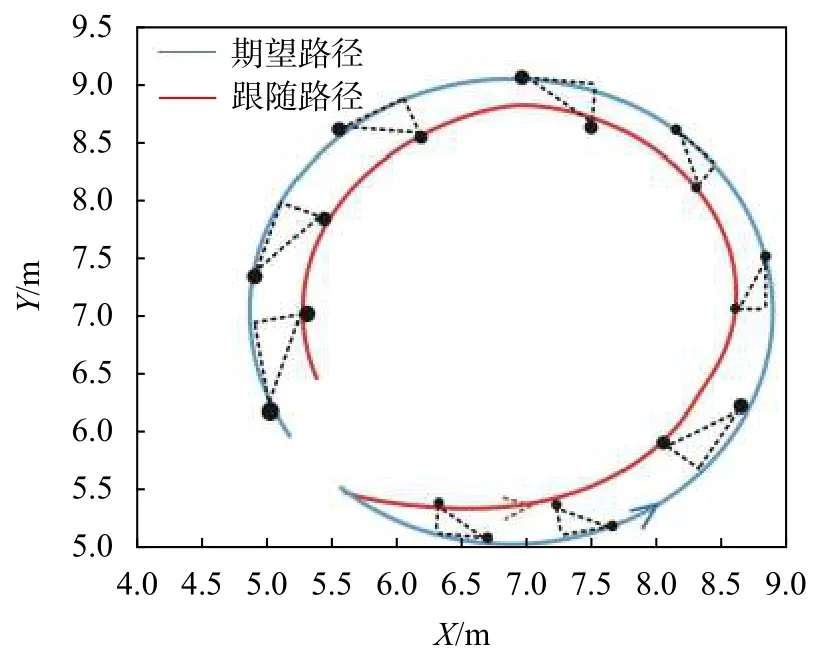
图12 λ=[0.5 π/6]T跟随机器人实验运动轨迹

领航机器人以0.8 m/s速度运动时，跟随机器人变化曲线如图13虚线所示。当时间趋于50 s时，跟随机器人速度稳定在0.8 m/s。

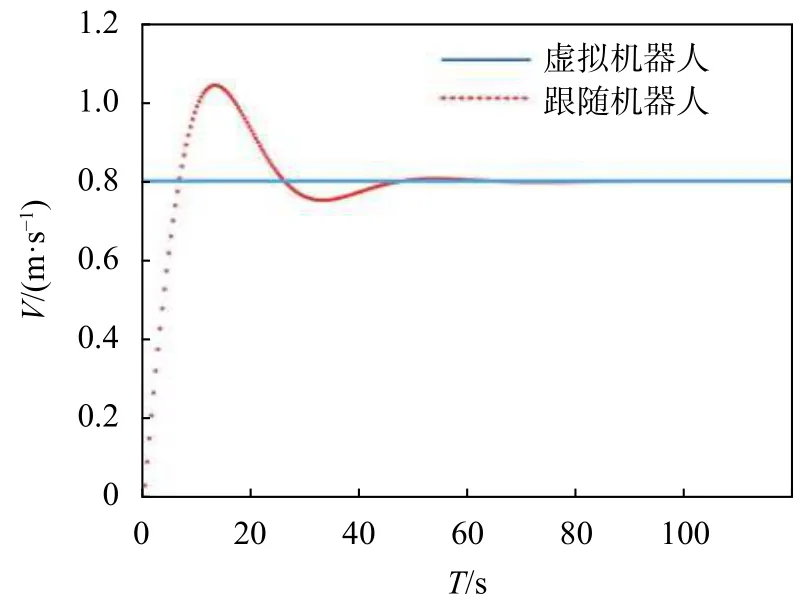
图13 λ=[0.5 π/6]T跟随机器人实验速度曲线

通过对比表2及前文中速度曲线可以看出，跟随机器人速度、位姿误差在仿真中收敛较快。并且，跟随期望轨迹比保持固定距离收敛耗时较少。

表2 仿真、实验结果

在一定时间内，跟随机器人运动速度逐渐收敛至预期，V0−V1在一定时间内趋于稳定。同时，跟随机器人与虚拟领航机器人位姿误差也趋近于稳定，系统达到稳定状态。

4 结束语

本文以轮式差分驱动机器人为实验对象，其由两个独立驱动的后轮控制，完成姿态变化。在此基础上，通过对差分驱动机器人运动学模型分析，设计了控制器并生成相应控制算法。利用仿真和硬件实验平台，在两种不同运动情况下，完成对控制算法的验证。仿真和实验结果表明：位姿误差收敛及速度收敛均能满足一般跟随控制需求，验证了控制算法与控制器的有效性与稳定性。

此外，本文提出的控制策略易于实现，只需合理设置 λ参数即可完成对机器人编队控制状态的调整，可为多种复杂场合下实际应用提供有益借鉴。