多传感器异步融合算法AUV对接导航系统

夏 楠，曾庆军，包灵卉，孙啸天，许赫威

（1.江苏科技大学电子信息学院，江苏 镇江212028; 2.中船海洋探测技术研究院有限公司，江苏 无锡214142）

0 引 言

海洋资源丰富但环境复杂，AUV是探索和开发海洋的新型手段。随着AUV的系统不断升级，性能也在逐渐加强。目前AUV正在向着高自主、高性能、长时间、远距离通信[1]等更智能方向发展。但是经过长时间工作，AUV需要精准的导航定位系统来引导AUV进行回收对接工作，方便布置新的使命[2]，和解决能源系统耗竭与提取内部数据的问题。

可靠的导航系统是AUV回收对接成功的重要保障。目前针对多传感器在组合导航系统中采样率不同的问题，几乎都是建立在各传感器数据传输都同步的理想状态模型下，在单一尺度下对问题进行分析。但在实际情况中，组合导航系统中各传感器的性能指标和采样频率各不相同，这就导致了多传感器组合导航系统量测信息滞后的问题，即产生异步采样问题[3]。因此对联邦滤波结构中异步融合算法的研究，对AUV回收对接工作具有重要意义。

针对组合导航系统中多传感器异步采样问题的研究，文献[4] 在组合导航系统中采用数据块分析技术，并提出了一种异步贯序滤波算法，融合各尺度经KF滤波优化的局部状态估计，最终得到全局最优状态估计值。算法使用要求各传感器的采样率是2的整数倍，实际应用比较受限。文献[5]提出多尺度数据分块的组合导航算法，主要在最细尺度下的系统模型中利用数据分块，将量测信息分解到各尺度进行滤波，得到全局最优状态估计值。此方法虽然提高了导航精度，但是增加了系统的计算量。

本文为了提高由于采样频率不同而致导AUV在回收对接过程中的导航定位精度较低的问题，提出了一种基于UKF融合的多尺度异步融合算法。本文算法依据采样率划分多尺度信息，建立基于联邦滤波的多尺度系统误差模型，并针对不同尺度信息采用UKF算法进行非等间隔异步融合，从而得到全局的最优状态估计。仿真表明，基于UKF的多传感器异步融合算法对AUV回收对接导航系统中异步采样信息具有更高的融合精度，提高了导航系统的精度和可靠性。

1 AUV回收系统原理

本文以江苏科技大学自主研发的“探海I型”自主水下机器人（AUV）的回收对接系统为研究对象。根据AUV的运动特性，可以把整个回收对接过程分为直线归位、直线跟踪、直线对接与惯性对接4个阶段。前面两个运动对接阶段的导航系统，为本文主要研究内容，此阶段AUV采用组合导航的方式。未进入USBL的作用范围时，主要由SINS的航位推算提供AUV的相对位置。当进入USBL的作用范围时，用多传感器融合的方式，提供AUV的相对精确位置，不断地调整AUV的位置与姿态，使其运动轨迹在对接坞在中轴线附近。而后在距离较近的直线对接阶段，采用双目视觉导航，使AUV机身对在对接坞的中轴线上，最后进入惯性对接阶段，依靠AUV运动惯性缓缓驶入对接坞。图1为回收对接流程图。

图1 AUV回收对接流程框图

如图2所示为“探海Ⅰ型”AUV实物图，其装配的传感器与相关参数如表1所示。

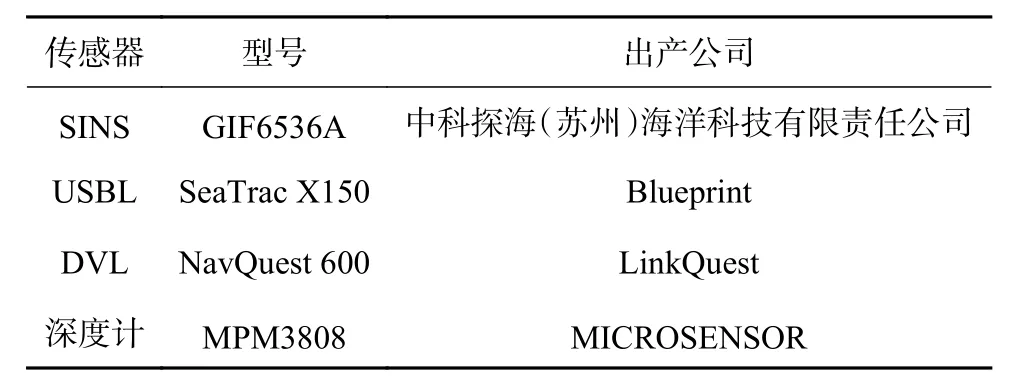
表1 传感器及相关参数

图2 “探海Ⅰ型”AUV

2 多传感器组合导航系统建模

图3 联邦滤波结构图

2.1 多传感器组合导航系统状态方程

选取导航系统的误差作为状态量，主要误差包括速度、姿态、位置、加速度计零偏和陀螺漂移[7]，USBL/DVL/深度计分别提供位置、速度、深度信息作为辅助则系统状态变量为：

式中：F（k）——系统状态转移矩阵；

W（k）——过程噪声矩阵；

G（k）——过程噪声驱动矩阵。

其中子系统的状态量X（k）为：

式中：δVE,δVN,δVU——东、北、天三个轴向的速度误差；

φE,φN,φU——东、北、天三个轴向的失准角；

δL,δλ,δh——纬度、经度、深度误差；

∇bx,∇by,∇bz——加速度计三个轴向的随机偏置误差[8]；

εbx,εby,εbz——陀螺的三个轴向随机漂移值。

由已知的系统误差模型，可建立子系统的非线性系统状态方程[9]为：

2.2 多传感器组合导航系统量测方程

本文设计的多传感器组合导航系统中，有3个子滤波器，每个子滤波器的量测方程：

1）取SINS位置数据与USBL转换后输出的位置数据作差为量测值，得SINS/USBL子滤波器量测方程：

式中：LSINS，λSINS，hSINS——SINS的纬度、经度和深度信息；

LUSBL，λUSBL，hUSBL——USBL的纬度、经度和深度信息；

DE，DN，DU——USBL沿东、北、天方向的位置测量误差；

RN——地球子午圈半径；

RM——卯酉圈的曲率半径[10-11]。

2）取SINS与DVL输出的位置数据作差为量测值，得SINS/DVL子滤波器量测方程：

3）SINS与深度计输出的位置数据作差为量测值，得SINS/深度计子滤波器量测方程：

3 多传感器异步融合算法

3.1 多传感器多尺度系统模型

假设用i=1,2,···,N来表示N个传感器，每个传感器对应的采样率为Ti，假设N为最细尺度，1为最粗尺度，ni∈N+，设传感器i和j之间的采样频率之比为A，则A为任意正有理数，即

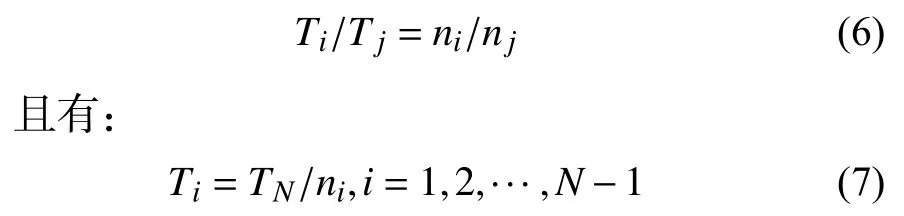
由多尺度模型分析可知，i表示传感器所在尺度，同时也表示其位数。本文设计的多传感器组合导航系统中，已知辅助参考系统在最高采样频率下的状态方程和观测方程[12]。第i=1个为低频采样传感器在最粗尺度上，第i=N个为高频采样传感器在最细尺度上。每个子传感器所在尺度各不相同，建立系统模型为：

可得，尺度i上k时刻的采样值与尺度N上nik时刻的采样值相对应，即可表述为：

可建立尺度i上的非线性系统状态方程和观测方程：

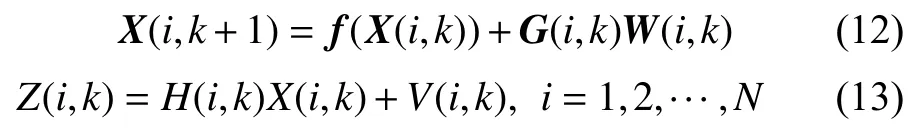
图4 多尺度异步采样示意图

3.2 多传感器异步融合算法建立

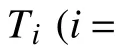
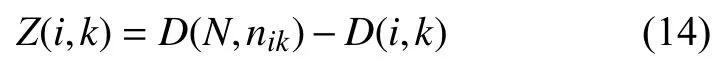
式中：D（N,nik）——nik时刻SINS的数据信息；

D（i,k）——尺度i上导航传感器在k时刻的量测值。

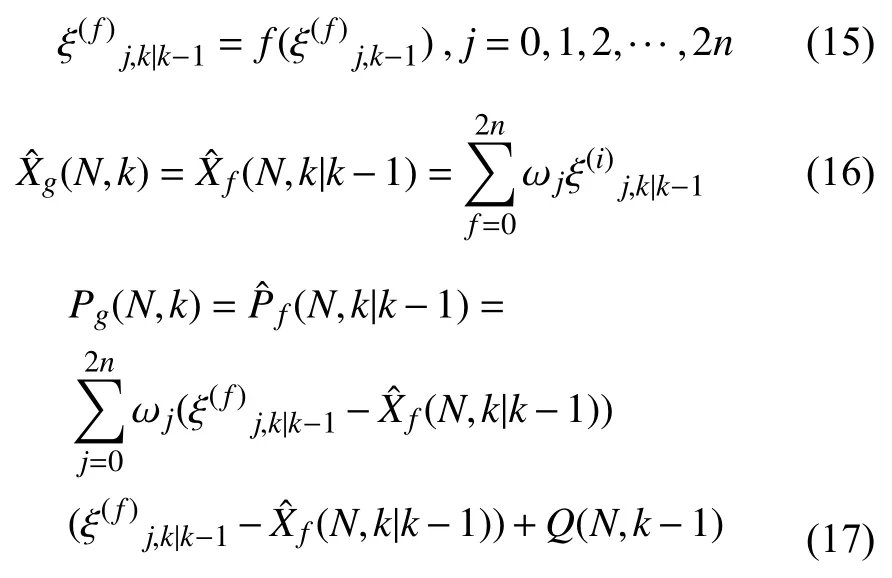
如图5所示为AUV对接导航系统中异步融合算法流程图。

图5 AUV多传感器异步融合算法流程图

4 仿真结果分析与湖试实验

4.1 仿真结果分析

为了验证本文设计的多传感器组合导航异步融算法在AUV对接导航系统中的有效性，利用Matlab软件进行仿真实验。仿真系统中对AUV水下航行的动态轨迹仿真以及利用导航传感器真实的误差数据仿真生成动态数据。如表2和表3所示，为所用传感器的误差参数和采样率。

表2 导航误差参数

表3 各传感器采样时间

表2中，由于AUV使用的深度计为400 m级大量程，所以精度最高在米级。

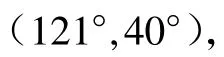
图6 AUV运动轨迹及状态估计

为了突出比较基于UKF的多传感器异步融合算法的优越性，针对速度、位置在同一运动轨迹上的误差，对三种不同的融合算法结果进行对比，表4所示为单一尺度状态估计和多尺度两种融合算法的状态估计标准差对比，图7为速度误差对比，图8为位置误差对比。

图7 AUV运动速度误差对比

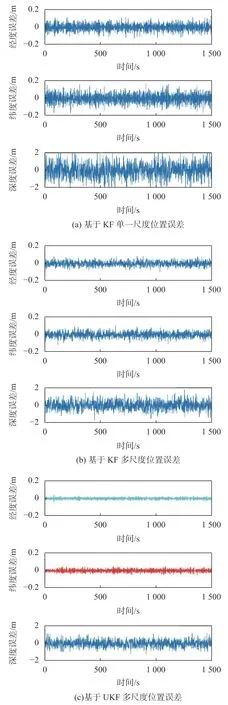
图8 AUV运动位置误差对比

表4 各参数标准差对比

仿真结果显示基于UKF的多传感器导航异步融合算法相对于基于KF的单一尺度融合算法和基于KF的多尺度融合算法更加稳定，滤波精度更高。本文设计的算法，有效的解决了由于采样频率不同而导致多传感器组合导航系统精度较低的问题，提高了AUV回收对接导航系统中异步采样信息的融合精度。

4.2 湖试实验

实验地选择在水域较为开阔的苏州某湖进行，便于试验开展，水深5～40 m，水流2节左右。如图9，为回收对接过程，图10为水面回收航迹图，表5为实验部分数据。

表5 部分实验数据

图9 回收对接实验

图10 水面回收航迹图

实验将对接坞固定在岸边码头，通过上位机规划AUV的目标点和深度的使命，到达目标点后开始自主对接实验。设置AUV速度0.8 kn（1 kn≈0.514 m/s），目标点坐标为（22,180），回收点坐标为（28.68,180.4），进行将近1.5 h的使命回收时间，对接实验成功。实验表明本文所设计的导航系统更加精准，在实际应用上为AUV的对接回收提供了安全保障。

5 结束语

本文为了提高由于采样频率不同而致导AUV在回收对接过程中的导航定位精度较低的问题，提出了一种基于UKF融合的多尺度异步融合算法。本文算法依据采样率划分多尺度信息，建立基于联邦滤波的多尺度系统误差模型，并针对不同尺度信息采用UKF算法进行非等间隔异步融合，从而得到全局的最优状态估计。通过Matlab软件针对实际系统进行仿真实验，相比于基于KF单一尺度算法与基于KF多尺度算法，本文基于UKF的多尺度异步融合算法具有更高的滤波精度和实际应用价值。湖试实验充分验证了AUV对接导航系统的有效性。