基于COMSOL的斜交轮胎成型机轴类零件优化设计
2021-12-13郭懿宁荣峰林伟青谢宇忱
郭懿宁,荣峰,林伟青*,谢宇忱*
(1.福建农林大学,福建 福州 350007;2.福建省建阳龙翔科技开发有限公司,福建 南平 354200;3.福建省轮胎成型装备重点实验室,福建 南平 354200)
轮胎作为随处可见的工业成品,在人们的日常生活中扮演着重要的角色。一个轮胎的生产要经过密炼、胶部件准备、轮胎成型和硫化四道工序,从碳黑、橡胶、油、添加剂等原材料加工成为一个成型的轮胎,再经过最终检验和测试即可投入使用。而轮胎成型这一步在四道生产工序中尤为重要,轮胎成型装备也是轮胎生产制造过程中最重要的设备之一。
福建建阳龙翔科技开发有限公司,是一家专业生产轮胎成型装备的工厂,是首批福建省轮胎成型设备重点实验室和工程技术研究中心,产品荣获国家专利三十多项,有着较为完善的轮胎成型装备生产流水线。由该公司开发的斜交轮胎成型机中,轴类零件受载情况较为单一,在设计中没有进行同步的仿真分析及机械校核。为了生产出的机械满足实际的工作需要,且强度、刚度等方面符合要求,其设计的零件所使用的材料过多,已经大大满足了实际的生产需求。且在机器零件的受载能力及受载后应力、形变等情况上没有科学的分析依据。
本文对斜交轮胎成型机中的轴类零件进行优化设计,根据优化结果,在满足设计需求的基础上,节约生产原材料,降低生产成本,提高经济效益。
1 尾座主轴的三维模型
尾座主轴由两段内径204 mm,外径260 mm的管用螺栓连接而成,总长3 985 mm。其中有1 700 mm长度在尾座箱体内,另外一段承受正反包的重力。三维模型如图1所示。
图1 尾座主轴三维模型
2 尾座主轴的优化设计
2.1 尾座主轴的优化思路
尾座主轴由两根管连接而成,受载以后形变的最大值发生在轴的最右端。且轴的最右端在实际生产中需要与另一边轴相互配合,所以轴的最大形变值应该是在优化设计时需要限制的一个重要变量。
COMSOL软件中优化模块有多种优化算法,在此选择使用Nelder-Mead算法,通过计算多个解,逐渐收敛至最后的最优解结束。在优化设计的过程中需要设置控制变量和参数,还有约束。对尾座主轴的优化设计,最后的结果是希望在最大形变值不增大的情况下,减小管的壁厚,从而达到在轴符合设计要求的情况下节省材料的目的,完成优化任务。
由于尾座主轴左端的管在箱体内,右边的管悬臂且要承受正反包的重力。所以左端管受载较小,可以作为主轴优化的目标。右端管作为主要受载部分,不对它进行改动,防止对整个轴的强度产生较大影响。
在尾座主轴的整个优化过程中,最大形变值应该是一个约束,限制了优化的结果。具体的优化变量是左端管的壁厚,由于管的外径要与尾座箱体配合,所以优化的目标为管的内径,通过增大管的内径达到减小管壁厚的结果。最后得出在最大形变值不超过我们的要求且最大时,左端管内径取到最大值,即管壁此时最薄,达到优化目标。
2.2 尾座主轴的优化设置步骤
将尾座主轴的三维模型导入COMSOL中,由于后续要将最大形变值作为优化设计中的约束,所以在最开始给有限元模型添加一个域探针。探针探测区域选择所有域,探针类型设置为最大值,由于需要约束的是形变的最大值,所以表达式设置为solid.disp。这个域探针的作用是实时显示尾座主轴上形变的最大值,可以用来设定为之后优化的约束。
然后在几何中新建平面,分割对象,定义材料属性,设置载荷和边界条件,剖分网格。有限元建模完成后,开始对优化计算进行设置。由尾座主轴的有限元分析可知,主轴的形变最大值发生在轴的最右端,大小为0.74 mm。为了优化结果更加安全,将0.74 mm限制为0.64 mm以内。算法选定Nelder-Mead,为了结果更加精确,将优化容差设置为0.001。目标函数设置为刚刚设定的域探针comp1.dom1,类型为最大化。
然后开始设置控制变量和参数,选定左端管的内径为控制变量,在将三维模型导入COMSOL中时,软件自动生成参数LL_D2_1,初始值为半径102 mm。将控制变量的下界设置为95 mm,上界设置为11 5mm。允许左端管的内径在95~115 mm的范围内变化。
最后设置约束。将域探针comp1.dom1设置为约束,下界设置为0.01 mm,上界设置为0.64 mm。则域探针会在0.01~0.64 mm中取到最大值。到此,优化设置完成,开始优化计算。优化设置如图2所示。
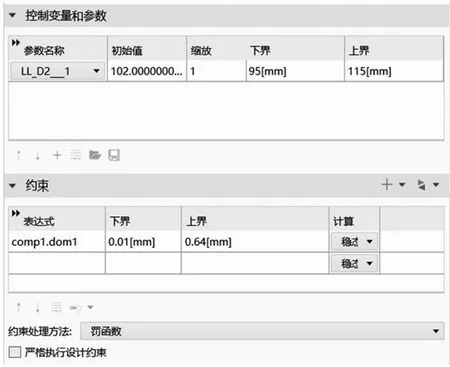
图2 尾座主轴优化设置
2.3 尾座主轴的优化结果
优化计算的过程,是在计算当左端管内径不同大小时,与之对应的尾座主轴的最大形变值。要求管内径要在95~115 mm中尽量取较大值,但作为约束的域探针给出的对应的形变最大值也要在0.01~0.64 mm以内,不能超出这个范围,同时形变最大值也要取较大值。因为内径与形变最大值是共同增加的关系。内径变大时,管壁变薄,轴的强度减小,形变也会越大。
优化计算以后,得出的内径最大值为112.28 mm,取整为112 mm。优化过程中探针图如图3所示。

图3 探针收敛图
最终管内径由102 mm变为112.28 mm,优化前,尾座主轴质量671.256 kg,优化以后,主轴质量578.728 kg,节省材料45钢92.528 kg。优化后尾座主轴三维模型如图4所示,应力图如图5所示,形变图如图6所示。
图4 优化后尾座主轴三维模型
图5 优化后尾座主轴应力图
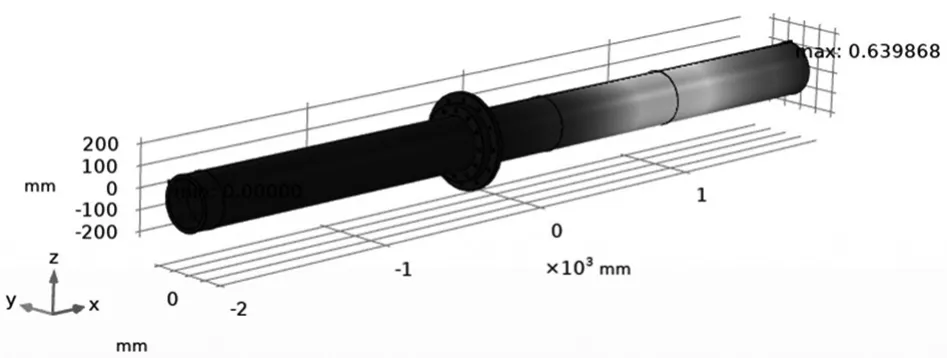
图6 优化后尾座主轴形变图
3 扩导主轴的三维模型
扩导主轴一端在扩导箱体内,另一端上安装扩导机械,负责运送帘布到轮毂上。扩导部分的三维模型如图7所示。

图7 扩导主轴三维模型
4 扩导主轴的优化设计
4.1 扩导主轴的优化思路
扩导主轴的受力情况与尾座主轴类似,对扩导主轴的优化方案也与尾座主轴相似。扩导主轴内径150 mm,外径190 mm,总长4 116 mm,其中640 mm位于扩导机箱内。主轴悬空承重的部分较长,长达3 456 mm,且需承重650.718 kg。根据扩导主轴的有限元分析,可知扩导主轴的最大形变发生在轴的最右端,且有6.96 mm的形变量。所以对于扩导主轴的优化主要放在箱体内的部分,对于箱体外的承重部分不进行改变。
对于扩导主轴的优化,同样采取COMSOL中的优化模块的Nelder-Mead算法。处于箱体内的管的壁厚为优化变量,主轴的最大形变量为约束条件。经过优化计算以后,希望在不增大最大形变量的情况下,尽量减小壁厚,节约原材料。
4.2 扩导主轴的优化设置步骤
首先将扩导主轴的三维模型导入进COMSOL软件中,然后对其定义材料属性,施加载荷与边界条件,剖分网格。由于需要将扩导主轴的最大形变量作为优化过程中的约束条件,所以需要设置探针探测不同壁厚情况下,主轴的最大形变量。在组件-定义中新建域探针,选择对所有域施加探针。因为要探测的是主轴的最大形变量,所以在表达式中选择solid.disp,计算物体发生的位移。探针类型选择最大值,在测量位移后,探针会以最大位移为结果显示。
设置完成域探针后,在研究中新建优化模块,开始对优化过程进行设置。首先选择优化算法为Nelder-Mead算法,优化容差调节为0.001。目标函数设置为刚刚新建的域探针comp1.dom1。由于我们需要优化结果在不超过要求的形变量的前提下,还要无限接近设置好的最大形变量,所以目标函数的类型选择为最大化。控制变量和参数设置为需要优化的640 mm管的内圆半径,当半径越大,管壁越薄,反之,则越厚。选择三维制图中的草图10-D1,管内圆半径。在将这个参数导入COMSOL中后参数名称为LL_D10___1,初始值为75 mm。设置其下界为65 mm,上界为85 mm。然后开始定义约束,约束选择设置好的域探针,表达式选择comp1.dom1。由于其最大形变量为6.959 mm,设置优化过程中最大形变量不超过7 mm。下界设置为6.2 mm,上界设置为7 mm。优化设置完成后,开始优化计算。优化设置如图8所示。
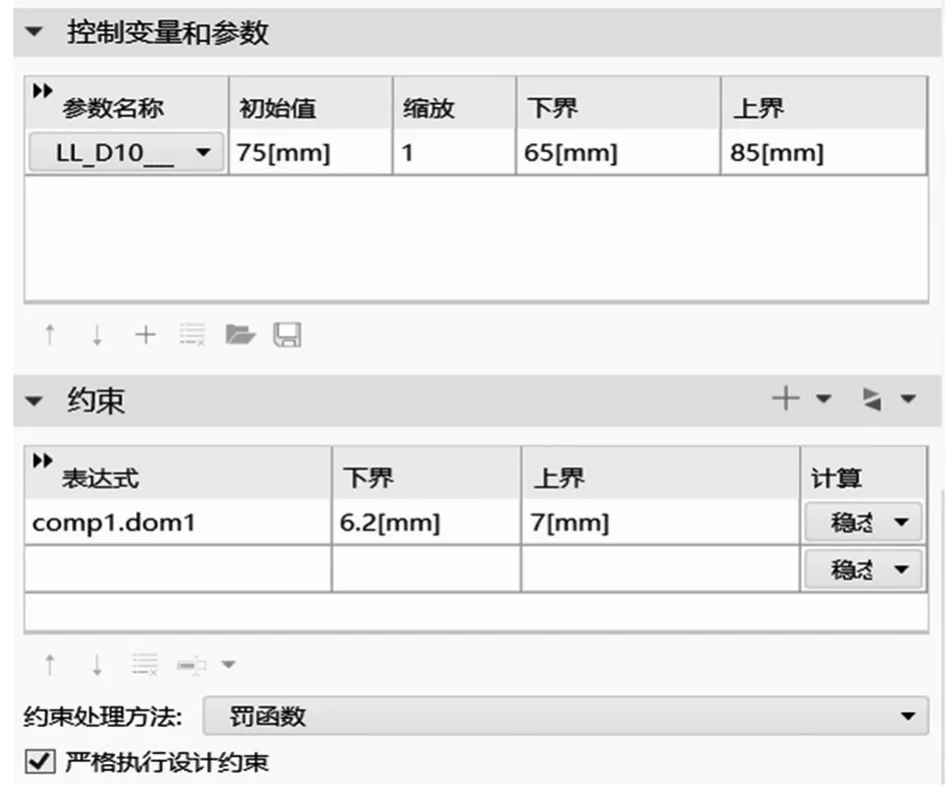
图8 扩导主轴优化设置
4.3 扩导主轴的优化结果
扩导主轴的优化过程,是计算扩导主轴的管内径在65~85 mm中取不同值时,与之对应的最大形变量。要求最大形变量取值要在6.2~7 mm之间,且尽量取最大值。优化过程如图9所示。
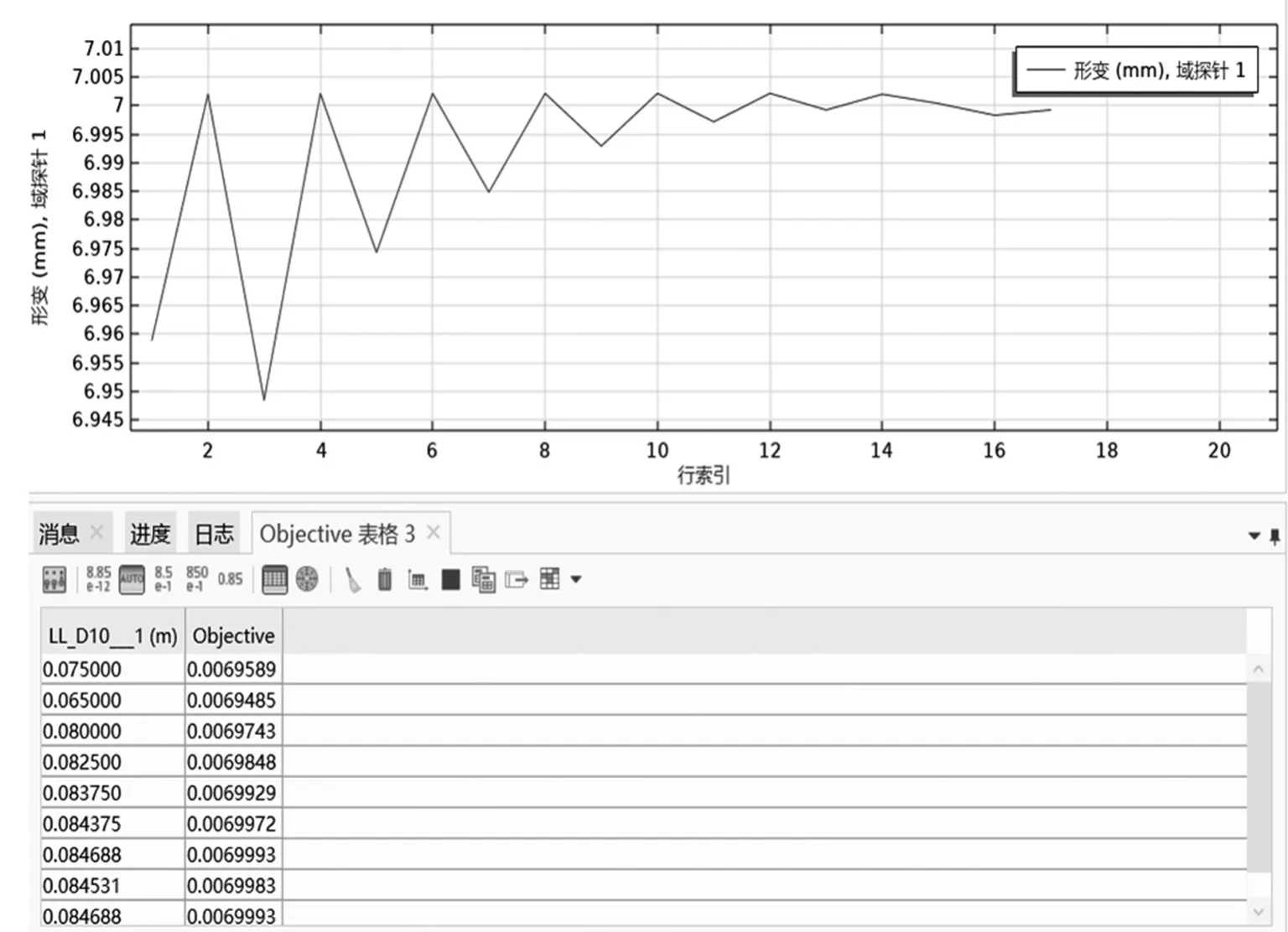
图9 探针收敛图
最终得到的优化结果为0.084 688 m,取整后为84 mm。管的内径由75 mm变为84 mm。优化前,扩导主轴质量为327.403 kg,优化后,扩导主轴质量为303.318 kg。节约材料45钢24.085 kg。优化后扩导主轴三维模型如图10所示,应力图如图11所示,形变图如图12所示。

图10 优化后扩导主轴三维模型
图11 优化后扩导主轴应力图
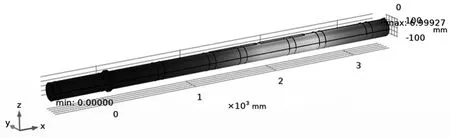
图12 优化后扩导主轴形变图
5 结论
本文主要对尾座主轴、扩导主轴两根主轴进行了优化设计,详细介绍了优化设计的思路及优化过程中的步骤和设置。最终完成的优化结果为,尾座主轴由671.256 kg减小为578.728 kg,节约材料45钢92.528 kg,质量减小约13.78%。扩导主轴由327.403 kg减小为303.318 kg,节约材料45钢24.085 kg,质量减小约7.36%。轴类零件共节约45钢材料116.613 kg。截止论文完成当日,45钢原材料价格为每千克4.2元人民币,所以,本论文设计约节约生产成本490元。由于轴类零件在实际生产过程中,是直接购买钢管进行加工,本设计对轴类零件进行优化后,可以直接采购管壁更薄的钢管,所以实际节约生产成本要更高于490元。
希望在未来其他机型的轮胎成型装备的生产上,本文中的成果可以对其他机型轴类零件的生产分析和优化设计起到参考作用。对于即将投入生产的机型,文中优化设计的结果可以投入到实际生产中,节约生产成本,提高公司的经济效益。
