制动盘自由模态仿真与试验对比及模态置信度研究
2021-12-13周长峰张家豪刘立邦刘新磊王希波
周长峰,张家豪,刘立邦,刘新磊,王希波
(山东交通学院 汽车工程学院,山东 济南 250357)
作为汽车制动系统的核心部件,制动盘的振动、噪声特性对整车的噪声、振动和平顺(noise vibration harshness,NVH)性能有重大影响。通过模态分析的手段,对制动盘进行模态特性研究,可以为解决车辆制动时的振动和噪声问题奠定基础[1]。
陈晓鹏[2]通过改变测点数量对制动盘模态振型的差别进行了描述;褚志刚等[3]和陈国强等[4]通过试验与仿真结果的对比,验证了有限元模型的准确性;文献[5-7]通过对制动盘的试验模态分析,得到了模态振型与噪声的关系;文献[8-10]通过仿真求解制动盘模态,并对其进行结构优化;焦标强等[11]和谭祥军等[12]通过试验的手段对制动盘进行模态分析,研究了参数辨识过程中的影响因素。目前的研究大多是单纯的仿真或是通过仿真与试验结果对比来验证有限元模型的准确性,对试验结果的准确性判断并未过多研究。
本文对某汽车制动盘进行计算模态分析,得出制动盘前五阶模态特性,并通过频率响应函数(frame repetition frequency,FRF)和模态判定准则( modal assurance criteria,MAC)对试验模态结果进行置信度研究[12],最后对比仿真与试验结果,验证所建模型的可靠性。本文所建立的模型可对制动盘使用状态下的振动特性进行预测。
1 制动盘的建模与自由模态仿真
1.1 制动盘建模
本文分析的制动盘外径0.276 m,凸台内径0.070 m,高度0.047 m,构建制动盘CAD模型后,将其导入Hyperworks软件,经过几何清理,去除细小边,生成有限元模型如图1所示。由于制动盘顶部壁厚较小,因此划分体网格大小约为2 mm,共508 710个单元,116 106个节点。制动盘的材料为HT250,其参数选用文献[3]中的材料参数,E=117 000 MPa,μ=0.27,ρ=7×10-9t/mm3。

图1 制动盘有限元模型Fig.1 Finite element model of brake disc
1.2 制动盘模态仿真
制动盘自由状态下各阶模态如图2所示。自由状态下,制动盘前五阶弹性模态频率分别为1 126.9、1 129.2、2 618.8、2 619.3、2 624.4 Hz。
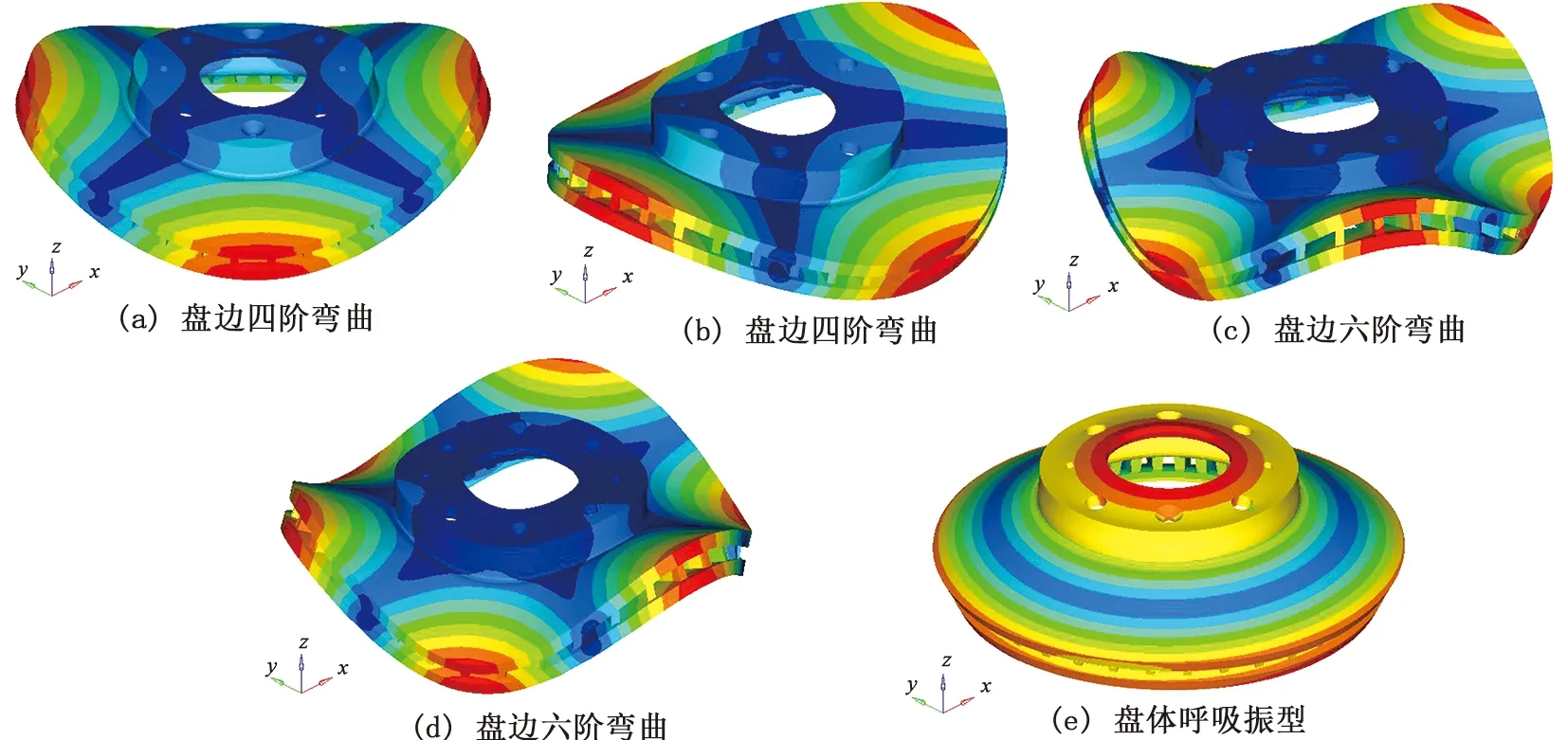
图2 自由状态下制动盘各阶模态仿真结果Fig.2 Modal simulation results of brake disc in the free state
由图2可以看出,制动盘的模态振型可分为制动摩擦面以及摩擦面与凸台组合的变形,图2(a)、2(b)的振型为盘边的四阶弯曲,二者为重根模态,除振型之间存在一定的角度差,其模态频率、模态振型基本相同。图2(c)、2(d)为盘边的六阶弯曲,二者也是重根模态,区别在于其节径与x轴之间的夹角不同。图2(e)为制动盘盘体的呼吸振型,该振型存在一个节圆。从上述结果可以看出,前四阶模态为摩擦面模态,第五阶为摩擦面与凸台的组合模态,仿真表明更高阶的摩擦面模态还包括盘边八阶弯曲、十阶弯曲等,更高阶的摩擦面与凸台的组合模态包括凸台的伸缩变形等,因此在制动盘更高阶的模态频率分析中,摩擦面模态、摩擦面与凸台的组合模态一定会交替出现,而且也一定会出现更多的重根模态。
2 制动盘模态测试
模态测试通过计算被测结构的频率响应函数,得到结构的模态参数。通过模态测试,可以评价结构的动态特性,对结构的振动故障进行诊断和预报,判断振动发生的根本原因,验证有限元模型的准确性。在模态测试前,首先要制定制动盘的测量方案。
2.1 制动盘测量方案
以制动盘中心轴线为z轴,制动盘的几何形状关于x、y坐标轴对称,其属于典型的回转体零件,因此在试验时可选择圆柱坐标系进行建模,采用半径r、角度θ、高度z这三个坐标描述测试点,制动盘x、y轴方向的刚度,远大于z轴方向的刚度,前几阶振动主要沿z轴产生,因此只采集各测点z方向的加速度即可。
制动盘整体质量较小,粘贴传感器时,应注意减小附加质量的影响,可采用多点激励、多点拾振的方法进行,激励为z向,加速度传感器的方向与圆柱坐标系三个方向一致。由前述仿真结果可知,若完整描述盘边四阶弯曲,需要在盘边测8个点,而完整描述盘边六阶弯曲,需要在盘边测12个点,但上述点的角度、方位是不同的。因此为保证试验时得到完整的上述振型,取上述两种振型测点数的最小公倍数,即在整个圆周上布置24个测点,一共布置5层,共120个激励点,测点的编号为逆时针编号,由外向里,编号逐渐增加,如图3所示。

图3 制动盘测点布置图Fig.3 Measuring points graph of brake disc
试验时将制动盘用弹性绳悬挂起来,如图4所示。因为制动盘固有频率较高,利用lms impact模块进行测量,频率范围选为0~3000 Hz。试验时4个加速度传感器沿周向均布,以防破坏结构的对称性。试验采用传感器固定,移动力锤的方式进行,每敲击一个测点,采集一组数据。

图4 制动盘自由模态试验悬挂图Fig.4 Free modes experimental graph of brake disc
2.2 制动盘试验模态
利用lms polymax软件对测试数据处理,得到的稳态图如图5所示。

图5 lms软件分析所得稳态图Fig.5 Stabilization graph obtained by lms software analysis
从图5中可以看出,制动盘传递函数固有频率非常明显,选取稳定点较多的位置,就可以确定制动盘的固有频率,进一步计算得到比较明显的模态振型,如图6所示。由图6及表1中的数据,对比仿真得到的模态振型,仿真和试验所得模态振型相似、模态频率接近,模态频率的误差小于3%,说明所建制动盘有限元模型准确度较高,该模型可用于约束状态下制动盘模态特性的预测。

图6 自由状态下制动盘试验模态Fig.6 Experimental modes of brake disc in the free state

表1 制动盘仿真模态与试验模态结果比较
2.3 模态验证
模态验证就是对模态参数估计结果的正确性进行检验。除了经验判断之外,还有许多手段进行验证。第一级验证方法是把试验得到的FRF与从模态参数识别过程中综合得出的FRF进行比较;第二级验证是用模态置信准则(MAC)等数学工具来检验估计的模态质量。
试验模态分析对测量所得FRF进行曲线拟合,能够得到结构的模态参数,根据拟合确定的模态参数又可以得到综合的FRF。在模态验证阶段可对比试验FRF与综合的FRF,得出二者的相关性与误差,二者的一致性主要受分析带宽、残余项和噪声等因素的影响。在制动盘上随机选择两个测点,上述两点的试验FRF与综合FRF对比如图7所示。结果显示二者在分析带宽内一致性较好,验证了试验所得模态参数的正确性。

图7 制动盘测点试验FRF与综合FRF对比Fig.7 Comparison of measured FRF and comprehensive FRF of brake disc measurement points
MAC是振型向量之间的点积,用于评价两个模态振型向量几何上的相关性,如果MAC值接近0,表明两个振型向量之间是正交的;若MAC值接近1,说明这两个振型向量彼此平行[13]。MAC矩阵中对角元素是各阶振型向量与自身的点积,因此MAC值为1,非对角元素为不同振型向量之间的点积,MAC值接近于0。制动盘振型MAC矩阵如图8所示,从图中可以看出MAC矩阵中非对角元素值很小,表明试验测试得到的制动盘前五阶模态就是制动盘本身的固有特性。
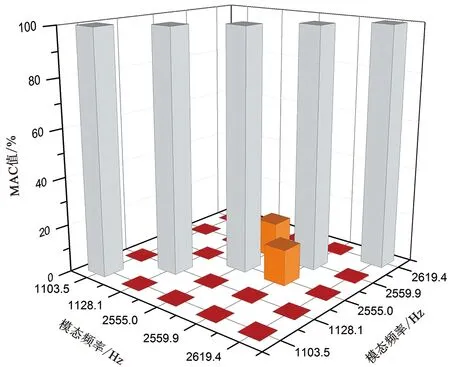
图8 制动盘振型MAC矩阵Fig.8 Vibration shape MAC matrix of brake disc
3 结语
(1)测量并建立了制动盘有限元模型,仿真得到制动盘自由状态下前五阶弹性模态,其频率分布范围为1000~3000 Hz。在这五阶模态中,有两组重根模态。
(2)模态测试前,可以根据仿真模态所关心的振型测点的最小公倍数,确定制动盘每周所布置的测点数。宜采用圆柱坐标系,多点激励、多点拾振的方法对制动盘等回转体零部件进行模态试验。通过试验能准确地测试得到自由状态下制动盘前五阶的弹性模态,包括摩擦面模态,摩擦面与凸台的组合模态,其振型分别为制动盘盘边的四阶弯曲、六阶弯曲和制动盘的呼吸振型。
(3)由试验模态参数得到的综合FRF与试验FRF相吻合;模态置信准则矩阵中非对角元素值很小。这些分析结果表明,试验测试得到的制动盘前五阶模态就是制动盘本身的固有特性。试验结果与仿真结果相吻合,表明了所建仿真模型的准确性。
从分析结果也可以看出,在制动盘更高阶的模态频率分析中,摩擦面模态、摩擦面与凸台的组合模态一定会交替出现,而且也一定会出现更多的重根模态。
