Lagrange函数的几何引入

贺慧霞， 苑 佳

(北京航空航天大学 数学科学学院，北京 100191)

0 引言

多元函数的条件极值是数学分析重要的研究内容，它不仅在经济生产和现实生活中有着广泛的应用，还在物理学、生物工程、化学等多个学科领域有着重要的作用.但它的求解方法一直是数学分析学习中的一大难点，条件极值问题除了一小部分可以通过消元法求解之外，绝大多数是通过Lagrange乘数法求解的[1-2].目前使用的大多数教材中,Lagrange函数的引入都是从极值的必要条件入手，通过严谨的分析得到的[3].但因为缺少几何直观，函数的引入显得不是很自然，我们将从一个具体例子入手[4]，借助几何直观，自然地引入Lagrange函数，给出Lagrange乘数法，并通过实例总结Lagrange乘数法的解题思路及解题步骤.

1 条件极值

下面我们通过一个例子来探索这类题目的求解方法.

例1求双曲线xy=3上的点到原点的最小距离(如图1).

图1

我们称解题的方法为消元法，然而,在一般情形下条件组中解出m个变元并不总是可能的，因此我们有必要探索新的、不直接依赖消元而求解条件极值问题的有效方法.

2 条件极值的几何求解

回到上例，我们来看一下其中蕴含的几何直观.

分析：目标函数z=f(x,y)=x2+y2，约束条件φ(x,y)=xy-3=0,由等高线的定义可知，函数z=x2+y2的等高线是x2+y2=c，是xOy平面的一系列同心圆.

图2

目标：求双曲线xy=3上的点，使得过该点的同心圆的半径最小.

图2

原问题转化为求f(x,y)=c与φ(x,y)=xy-3=0相切时x,y的大小(见图3).

图3

等高线与双曲线在切点处的法向量是平行的，即nf(P)//nφ(P),平面曲线g(x,y)=0的法向量为ng=(gx,gy)[5]，所以可知向量(fx,fy)与向量(φx,φy)线性相关,即存在非零实数λ,使得

(fx,fy)|P+λ(φx,φy)|P=0.

即切点坐标(x0,y0)满足方程组

(1)

3 Lagrange乘数法

观察方程组(1)，可知它是多元函数L(x,y,λ)=f(x,y)+λφ(x,y)的驻点方程组.上面的方法是否具有一般性呢？我们断言：

【断言】设函数f(x,y),φ(x,y)有一阶连续偏导数，则函数z=f(x,y)在条件φ(x,y)=0下的极值点满足三元函数L(x,y,λ)=f(x,y)+λφ(x,y)的驻点方程组.

(2)

称函数L(x,y,λ)=f(x,y)+λφ(x,y)为Lagrange函数，其中λ为Lagrange乘数，利用Lagrange函数求解条件极值的方法称为Lagrange乘数法[6].

在上面的证明中，我们只用到了隐函数定理、函数极值的必要条件和复合函数求导，因此求三元及三元以上的多元函数在多个约束条件下的极值时，只要目标函数和条件函数有一阶连续偏导数，也可构造出Lagrange函数.以三元函数u=f(x,y,z)在两个约束条件φ(x,y,z)=0,ψ(x,y,z)=0下的极值问题为例,可构造Lagrange函数

L=f(x,y,z)+λφ(x,y,z)+μψ(x,y,z).

4 用拉格朗日乘数法求解条件极值问题的一般步骤

4.1 根据问题意义确定目标函数与条件组，作拉格朗日函数

其中，m为条件组的个数.

4.3 判定所得驻点是否为所求的条件极值点.

判定所得的驻点是否为极值点有以下的一个充分条件[7]：

则当方阵H(P0)正定(负定)时，P0为f的条件极小(大)值点，因此f(P0)为满足约束条件的条件极小(大)值.

注记：当H(P0)不定时，并不能说明f(P0)不是极值.

在实际问题中往往遇到的是求最值问题，这时可以根据问题本身的性质判定最值的存在性，而不必验证[5,8].

解:设拉格朗日函数为

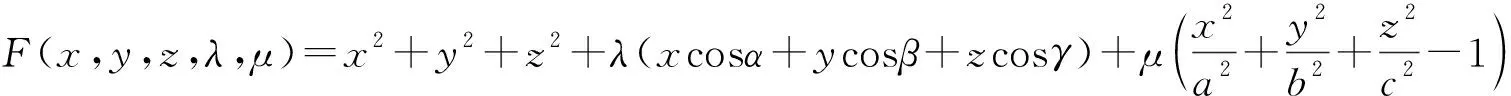
将(3)(4)(5)三式分别乘以x,y,z,然后相加可得

x2+y2+z2=-μ，即u(x,y,z)=-μ.可知要求的函数的最值由参数μ确定.

由式(3)、式(4)、式(5)可解得

代入式(6)可得

即

[a2cos2α+b2cos2β+c2cos2γ]μ2+[(b2+c2)a2cos2α+(a2+c2)b2cos2β+(a2+b2)c2cos2γ]μ+a2b2c2=0.

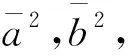
于是椭圆的面积为

拉格朗日乘数法是优化问题中一种寻找变量受一个或多个条件限制的多元函数的极值的方法.这种方法将一个有n个变量与k个约束条件的最优化问题转换为一个有n+k个变量的方程组的极值问题，其变量不受任何约束.这种方法引入了一种新的标量未知数，即拉格朗日乘数：约束方程的梯度(gradient)的线性组合里每个向量的系数.此方法的证明牵涉偏微分、全微分或链法，从而找到能让设出的隐函数的微分为零的未知数的值即为满足约束条件的极值.但是拉格朗日乘数法只能求极值，不能精确到极小值或极大值(像求导求极值一样)，所以求最值时要代入验证.本文从几何的角度解释了拉格朗日函数的构造思路，让读者在学习相关内容时更加容易接受和理解.