举网以纲 千目皆张——浙教版四年级下册第四单元整合实践与反思

文|谢琰翡 田秋月

钟启泉教授认为，“单元设计既是课程开发的基础单位，也是课时开发的背景条件。单元设计是课时计划的指引，是撬动课堂转型的一个支点”。怎样发挥单元备课的优势，更好地帮助学生深刻透彻地理解掌握所学知识技能、积累活动经验呢？

东汉哲学家桓谭《新论·离事》中提出“举网以纲，千目皆张”（提起绳子，一个个网眼就都张开了）的观点启发了我们对本单元备课的思考：如果在单元设计时抓住要点和主线，提纲挈领分清主次，就能帮助学生优化学习过程。

因此，结合学生思维认知特点分析教材知识脉络，找到本单元的学习“支点”，抓住单元学习的纲领性主线，沿着主线脉络再进行结构化的单元整合课时编排和课例设计，成为本文思考的关键。

一、教材分析

1.单元内容分析。

从教材目录（图1）可以看出，本单元教学内容包含了角的度量、角的分类、轴对称图形、图形的旋转、三角形内角和、图形的边与角、图形的高与底，即《数学课程标准（2011年版）》中所指的图形的测量、运动和认识这三个维度。

图1 浙教版《数学》四年级下册第四单元目录

2.知识序列分析。

纵向分析知识脉络（图2），本单元的学习内容除了轴对称图形、图形的高与底是第一次认识，其他内容都已在第一学段有过初步的认识。螺旋上升的编排旨在逐步达成《数学课程标准（2011年版）》所规定的此学段所需达成的教学目标与要求。本学段的教学任务在本单元的教学中体现为帮助学生对图形的认识走向更深刻、严谨、全面。例如，利用角的精确度量认识各类角，在操作中体会三角形、平行四边形、梯形的定义，并感知这些图形的数据特征，与此同时，学生对图形运动的探究也摆脱了第一学段笼统的描述性认知，转而用更加精准的概念表述。

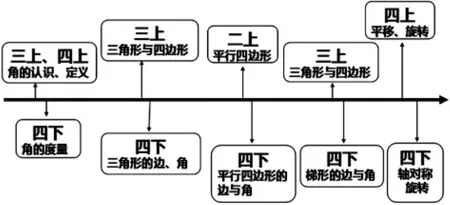
图2 相关知识脉络图

3.知识点梳理。

基于《数学课程标准（2011年版）》目标要求，梳理教材中每一课时的教学内容和知识点以及重难点：

（1）角的认识：作为单元起始课，本课重点是建构1°角，体验单位角的累加过程，体验量角器的产生过程。（2）角的分类：“平角、周角”概念不是难点，以直角为标准进行分类的经验可以直接利用。（3）轴对称图形：本课重点在于将原先关于轴对称图形的感性认知与数学中严谨的概念进行对接。（4）图形的旋转：本课以线段的旋转为起点，学习图形的旋转，进一步理解旋转三要素（旋转中心、方向、角度），“图形中的任意部分都旋转相同的方向与角度”的图示操作是难点。（5）三角形的角：可将角的分类迁移到三角形按角分类。（6）三角形的边：三角形的边分两个课时，第一课时主要涉及三角形按边分类，第二课时重在探究三边关系。（7）三角形的内角和：学生对“三角形的内角和是180°”的结论并不陌生，但探究三角形内角和过程中的策略、方法、活动经验必不可少。（8）平行四边形和梯形的认识：二者学习路径相同，从特点、概念、关系、角的特征四个方面去落实。（9）图形的高与底：作为浙教版教材的特色内容，图形的高与底独立成课，作为探究几何图形面积的基础，本课知识既是重点也是难点。

二、学生调研

1.设计前测试卷。

学习内容的整合需基于真实学情，通过前测（《四年级下册“几何小天地”单元前测卷》可通过二维码扫描获取）了解学生的认知起点，聚焦两个问题：一是学生对各知识点的已有认知是否与设想吻合？二是学生对相关知识点间的联系认知情况如何？

2.学生实测数据。

杭州市胜利实验学校160 名学生参与了前测，为确保测试信度和效度，以课堂作业的形式独立完成，教师不作任何干预。测试后各小题知识点与考查细目的正确率如下表（表1）：

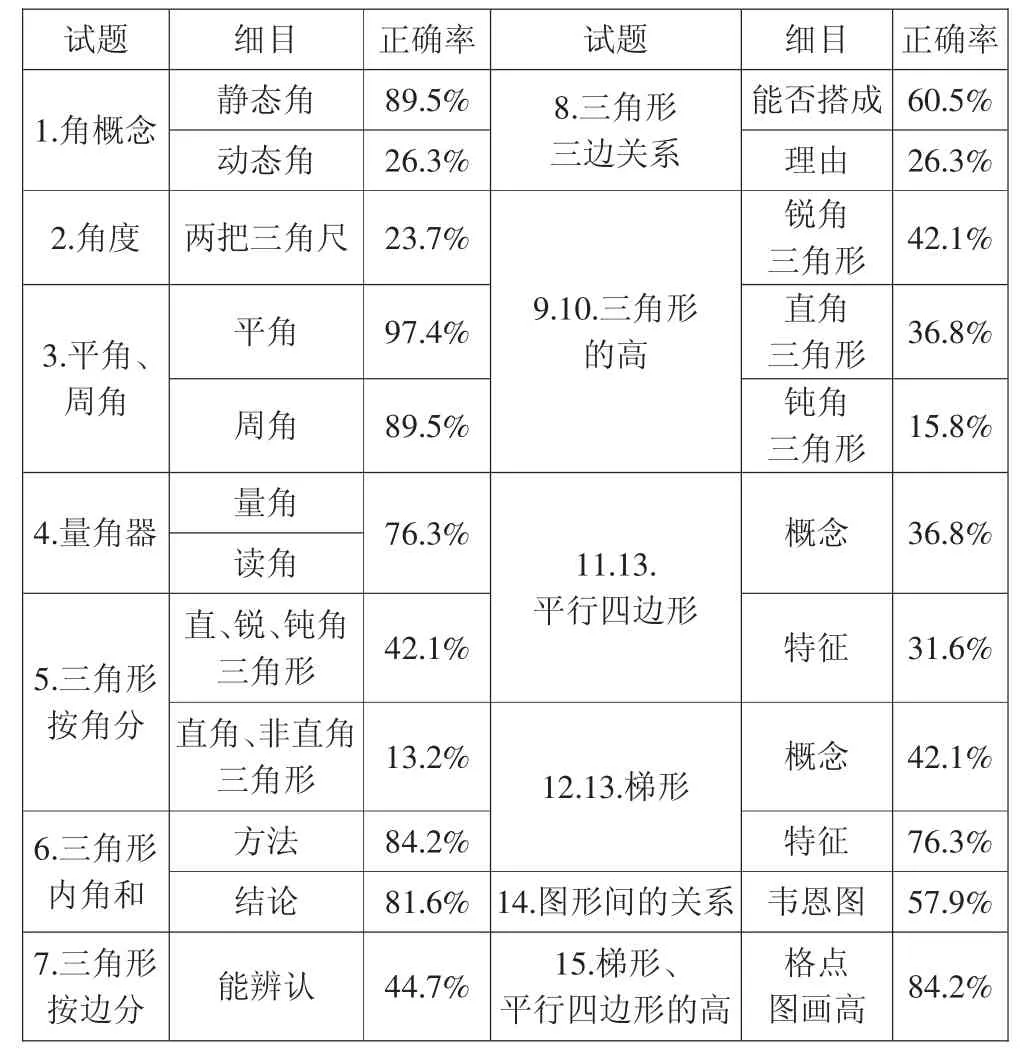
表1 单元前测知识点细目正确率

3.前测分析与思考。

根据上表数据，分析可得出以下思考和结论：

（1）76.3%的学生能正确使用量角器测量角的度数，但结合访谈可知，绝大部分学生不明操作原理、不能建构角度的计量单位“1°”角，因此，作为起始课的“角的度量”不可整合。

（2）89.5%的学生能将角分类，分别有97.4%与89.5%的学生对新知识“平角”“周角”的概念认识无障碍。

（3）建立在“角的分类”基础上的“三角形的分类”正确率达55.3%，学生在不同程度上对《角的分类》《三角形的分类》有一定知识基础，这两节课的整合有据可依、水到渠成。

（3）44.7%的学生能逻辑清晰地将三角形按边进行分类，但主动按边分类的意识十分薄弱。60.5%的学生能正确判断三根小棒是否可以围成三角形，但只有26.3%的学生能从根源上说明能否搭成三角形的原因。所以《三角形的边》不仅不能整合，还需增加基本的活动体验。

（4）图形的认识和特征判断中，梯形的认识正确率最高，达76.3%，说明梯形特征认知难度较低，而正确率低的平行四边形的认识和判断，只有31.6%。但是从访谈中了解到，学生不理解概念表述中的“对角”“对边”等名词术语，而非图形的特征理解，同时学生可以迁移探究三角形的特征的策略来研究平行四边形和梯形，所以《图形的边与角》一课可整合。

（5）图形作高正确率最低的是三角形的高，尤其是钝角三角形（正确率15.8%），而“图形的高与底”对于掌握图形特征、探究和计算图形面积非常重要，因此保留本单元对图形“高”的整体建构特色不变。

三、单元整合与重构

1.基于“纲领”主线的学习路径。

教材分析的设想与学生实际情况匹配成功，从单元全局主线来看，以学生立场，对学习路径进行了调整（图3），以此指导进一步的单元整合设计（图4），正如杜山老师所说，这一整合抓住单元内容中的本质共性，“进行板块化重组，以促进学生精准掌握相关内容的共性与联系，从而实现结构化的知识整合”。

图3 单元学习路径

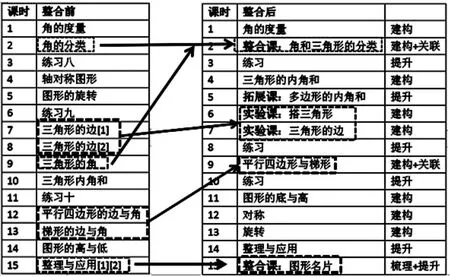
图4 单元整体框架目录

《角的分类》《三角形的分类》整合为《角与三角形的分类》，旨在以“角”的分类为“纲”，牵引三角形按角分类的“网”，并为后续探究平行四边形、梯形的角埋下暗线。

《平行四边形的认识》《梯形的认识》整合为《平行四边形与梯形》。平行四边形和梯形的探究完全可以迁移三角形的探究方法（图5），主线是“边的长度与位置”“角的大小”两个维度，牵引出这两种图形的本质属性。

图5 《三角形、平行四边形、梯形的认识》研究维度

以上单元结构化处理，从学习路径上帮助学生抓住纲领性知识的主线，不仅提升了学习效率，降低了认知难度，更重要的是将知识的理解引向更加深入的关系维度。

2.基于“千目”网络的逻辑关系。

《三角形的边》在教材中有一定的逻辑顺序（图6）：先任意选择三根小棒搭三角形，发现有些能够搭成，有些不能，于是分别研究不能搭成三角形的三根小棒长度有什么关系？由此得出“三角形任意两边之和大于第三边”的结论；能搭成三角形的三根小棒，不同的长度造成对应的三角形的形状区别是怎样的？于是开展“选”“换”“搭”（对称三角形）“变”这四步探究。因此这一内容可整合为系列课：实验课《搭三角形》、探究课《三角形的边》，抓住知识间的逻辑递进关系，帮助学生从不同的维度认识《三角形的边》，由多个局部的“千目”走向“整体”的统一认知。

图6 实验课《搭三角形》、《三角形的边》研究步骤

3.纲举目张，横纵相通。

整合之后使得课时有余，可增设练习课，将新知识进行综合运用，在跟进巩固和变式练习中提高思维梯度。此外，纵横拓展成为单元设计时纲举目张的措施。

在《三角形的内角和》之后，纵向拓展《多边形的内角和》；常规的《整理与应用》之后，横向增设综合实践课《图形名片》。学生根据自己的思维方式和偏好，自行选择思维导图、结构图、使用说明书等形式对本单元的学习进行系统的梳理，教师根据评价量规，指导全班开展交流、汇报，来自于学生的自主整理，也是一种学习资源，以此扩充教材的资源内容，启发学生主动建构具有个体经验的单元知识体系。

以上单元整合重构设计基于学情，关注学习路径，提纲挈领抓住知识学习主线，梳理逻辑关系打通知识网络关联，纲举目张拓展学习视野、丰富学习方式，巧妙地帮助学生找到单元学习的支点，将学科逻辑与自己的认知逻辑进行整合，从而由单纯知识和技能的学习深入到学会思维的学习中。