关注学生评价 叩响经验课堂
——《钉子板上的多边形》教学与思考(二)
2021-12-13王扣兰张云杰
文|王扣兰 张云杰
【教学内容】
苏教版五年级上册第108、109 页。
【教学过程】
一、创设情境,铺垫规律


师:今年是建党100 周年,同学们用自己的巧手表达了对祖国的热爱。回顾“绕线钉子板”制作的过程,想一想:什么决定了你所绕图形面积的大小?
生:我绕的第一幅图,发现边上的钉子越多,五角星的面积越大。
生:我同意,但我有补充。我绕的第二幅图,发现里面的钉子越多,五角星就越大,外面的圆及整幅图也相应就越大。
师:说得都有道理,老师从你们的“绕线钉子板”上“闻”到了一丝数学的味道。其实数学味更浓的钉子板还是我们的老朋友,(出示学具)这节课我们就借助它来研究钉子板上的多边形。
【设计意图:时值建党100 周年,学生利用假期以一幅幅精美的“钉子板绕线画”来表达自己的情感。“从经验中学习,经验是一切有价值的训练的源泉”,从学生的行为操作活动经验出发,以一个关键问题“什么决定了你所绕图形面积的大小”打开学生的思维,帮助学生认识知识的起点,激发学生的学习兴趣。】
二、实践研究,初探规律
1.起点认知。
师:老师在钉子板上围了两个平面图形:三角形(图①)和梯形(图②)。你能数数它们边上的钉子数吗?
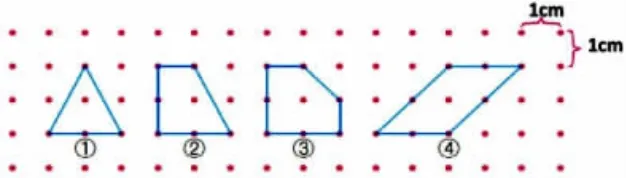
(学生数,教师随即板书)
师:如果每两个钉子之间的距离是1cm,那你还知道什么呢?
生:每个小正方形的面积是1cm2。
生:三角形的面积是2cm2。
生:梯形的面积是3cm2。
(根据学生的回答完善板书《学习单1》)
2.观察发现。
师:观察黑板上的这两组数据,你有什么发现?
生:面积是钉子数的一半。
师:仅仅根据这两个图形,能肯定这个发现吗?(不一定)是的,这仅仅是你们的猜想,我们还需要更多的数据来验证与支持。
3.验证猜想。
(1)研究例题的后两个图形。
师:这里还有一个五边形(图③)和一个平行四边形(图④),请数一数、算一算、填一填《学习单1》,想一想这样的规律还成立吗?
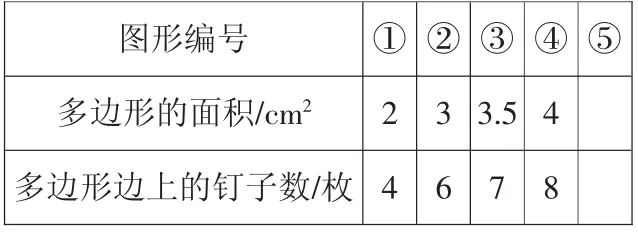
学习单1
(学生独立探究并交流汇报,后两个图形的数据也能证明猜想。同时,引导学生关注这些图形的面积除了可以计算之外,还可以数一数,特别是第三个图形,用数一数的方法更简单)
(2)研究课前自己围的图形。
师:现在这四个图形都能证明我们的猜想,那是不是所有图形都存在这样的规律呢?请同学们拿出课前围的平面图形(如下图),也请你数一数、算一算,然后填一填《学习单1》,思考:这样的规律还成立吗?
(学生独立计算,教师巡视收集资源:图形内部只有1 枚钉子:符合规律;图形内部钉子数不是1:不符合规律。组织交流,分别请两名学生代表上台汇报。如下图)
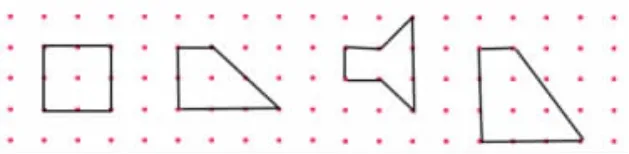
4.比较归纳。
师:为什么老师画的图形都符合规律,而你们画的图形,有的符合,有的不符合呢?小组观察《学习单1》上的四幅图,再对比大屏上的四幅图,有什么想说的?
生:我发现老师画的图形里面都只有1 枚钉子,我们画的符合规律的图形里面也只有1 枚钉子。
生:我同意,但我有补充。我发现不符合规律的图形,里面要么没有钉子,要么有2 枚钉子。
小结:看来多边形的面积,除了与边上的钉子数有关,还与它内部的钉子数有关。当多边形内部的钉子数是1 时,多边形的面积是多边形边上钉子数的一半。
师:当多边形内只有1 枚钉子时,用n 表示多边形边上的钉子数,S 表示多边形的面积,那么S=n÷2。
5.内化运用。
师:这一数学规律,是我们用多个例证一步一步探究而得的。那它有什么用呢?这是李明课前围的一只“茶壶”,你知道这只“茶壶”的面积吗?

生:3.5cm2。
师:你怎么这么快就知道的?
生:这个“茶壶”内部钉子数是1,边上的钉子数是7,所以面积是3.5cm2。
师:求“茶壶”的面积,如果用数或者算的方式,你感觉如何?
生:感觉比较困难。
师:请你评价一下这个规律。
生:这个规律能帮助我们快速解答钉子板上的多边形面积。
6.总结板书。
师:回顾规律得到的过程,我们是怎样一步一步走过来的?
(总结板书:观察—比较—猜想—验证—总结—运用)
【设计意图:波利亚曾说“学习任何知识的最佳途径,是自己去发现。因为这种发现理解最深刻,也最容易掌握其中的内在规律、性质和联系。”教师适时制造了一个认知冲突,“到底什么样的图形才符合规律呢”,学生通过观察比较,发现需要添加一个条件。这个环节不仅激发了学生刨根问底的探究热情,还为后面研究a≠1 做好铺垫。此环节教师适当地扶,让学生初步经历了探索规律的一般过程:观察—比较—猜想—验证—总结—运用,也让学生在自主归纳规律的同时,提升了符号意识、数据分析观念等。另外,教师特别注重评价研究:生生互评“我同意,但我有补充”;师生互评“你怎么这么快就知道的,你感觉如何”;过程评价“请你评价一下这个规律”,这样的评价性语言让课堂更有张力,更有深度。】
三、分组合作,拓展规律
1.合力探索。
师:用这个方法,我们探索出了内部只有1 枚钉子的规律,那接下来你觉得可以继续研究什么?
生:内部有2 枚钉子的多边形。
师:你们准备怎样研究呢?
生:我建议小组合作,团队的力量比较大。小组内四个人分别在钉子板上围一个不一样的内部有2 枚钉子的多边形,数一数、填一填,然后把其中三个人的研究数据合起来探索出规律,最后用这个规律来验证第四个人的图。
(小组合作,借助《学习单2》进行探究,教师巡视指导)
2.小组汇报。
交流汇报:小组上台汇报,展示四幅图形及《学习单2》,介绍小组的研究过程,说说小组的发现,其他小组及时补充。

学习单2
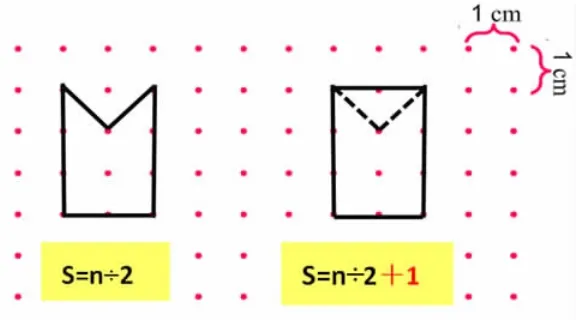
得出结论:当多边形内有2枚钉子时,S=n÷2+1。
3.数形结合。
利用多媒体技术展示多边形边上的钉子数不变,面积与内部钉子数的变化。明确S=n÷2+1 中,“+1”加的是哪部分?
【设计意图:“要想走得快,就一个人走;要想走得远,就结伴而行”。学生已经有了a=1 的探究经验,接下来自然而然地产生了a=2的探究内需,探究的形式是引导学生组成学习共同体,开展合作学习、互助式学习,让学生真正站在学习的正中央。】
四、推动内驱,完善规律
1.类比推理。
师:你还想研究什么?
生:内部有3 枚钉子、4 枚钉子、0 枚钉子……
师:根据内部有1 枚钉子和2枚钉子的规律,先猜猜内部有3枚钉子的规律可能是什么样的?
生:S=n÷2+2。
2.分组研究。
师:以小组为单位展开研究,开始前先明确活动要求。
活动要求:(1)议一议:每个小组确定一个研究主题;(2)画一画:小组成员按照研究主题完成《学习单3》;(3)理一理:组长收集并汇总成员研究信息;(4)说一说:观察表格,小组交流,共同汇报研究成果。
(学生小组合作探究并完成《学习单3》)
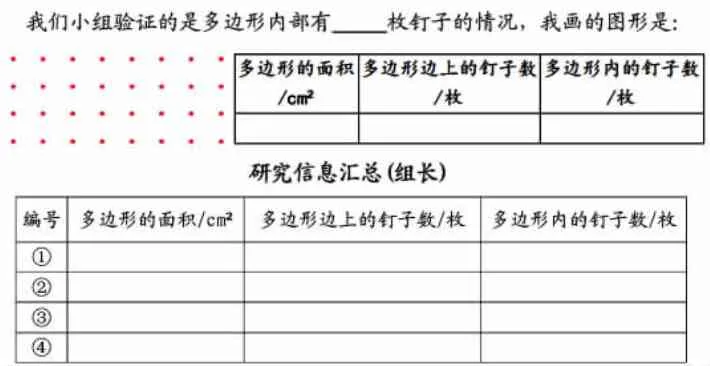
学习单3
得出结论:当多边形内有__枚钉子时,S=______。
3.交流成果。
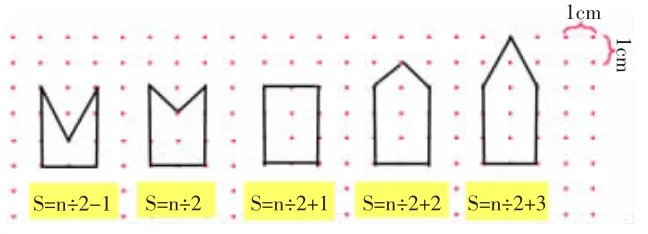
分组汇报:钉子板内部有0枚钉子时,S=n÷2-1;钉子板内部有3 枚钉子时,S=n÷2+2;钉子板内部有4 枚钉子时,S=n÷2+3。
师:照这样写下去,5 枚呢?6枚呢?10 枚呢?你有什么发现?
生:前面都是n÷2;后面加的数比内部钉子数少1。
师:你能用一个简洁的表达方式概括出这里所有的规律吗?
生:钉子板内部有a 枚钉子时,S=n÷2+a-1。(板书)
4.深化认知。
师:下面,我们用一组动画来感受规律的由来。
五、运用规律,拓展认知
1.运用规律。
师:下图中喇叭、小猫、小狗的面积各是多少?

生:喇叭边上钉子数是8,内部钉子数是0,则S=8÷2-1=3cm2。
生:小猫边上钉子数是20,内部钉子数是2,则S=20÷2+1=11cm2。
生:小狗是两个多边形的组合。身体面积:S=12÷2-1=5cm2;尾巴面积:S=4÷2-1=1cm2;总面积:5+1=6cm2。
2.回顾过程。
师:回顾探索和发现规律的过程,你有什么体会?
(学生自由说)
3.拓展规律。
师:同学们,今天所学的规律也叫“皮克定理”。我们一起来看看关于“皮克定理”的微视频。说一说,有哪些异同点?
生:表示面积、内部钉子数和边上钉子数的字母不一样,但规律的本质内涵是一样的,都是用“边上钉子数÷2+内部钉子数-1”。
师:真是一群会思考、能探究、善总结的孩子!通过一节课的努力,不仅探索出大数学家皮克发现的定理,还能灵活运用。老师希望你们能保持这样的探索热情,一直这么深度思考下去!
【设计意图:教师是学生的镜子,学生是教师的影子,教师关注什么,学生就能得到什么。探索规律,重在探索二字,让学生学会思维,经历过再三的思考直至它在个人经验中生根。整节课,学生经历了“发现—会发现—爱发现”的学习过程,寻幽探径,这样的学习过程、发现过程是学生自己创生的,如此便是深度学习。】
