基于潜子空间去噪的子空间学习图像分类方法

杨章静，王文博，黄 璞，张凡龙

南京审计大学 信息工程学院，南京 211815

图像分类是计算机视觉领域的一个研究热点[1-3]，子空间学习（subspace learning，SL）是机器学习领域的一项重要技术，它在数据分析、数据降维、图像分类等方面取得了显著的成果[4-7]。由于其求解方便、时间复杂度低等优点，广泛应用于图像分类领域。

图像分类领域有许多经典的算法，如最近邻分类器（nearest neighbor classifier，NNC）[8]、稀疏表示分类器（sparse representation classification，SRC）[9]、线性回归分类器（linear regression classification，LRC）[10]、协同表示分类器（collaborative representation classification，CRC）[11]等，它们都基于惰性学习，当数据量较大时，分类速度会变慢。基于SL 的方法在训练完成后即可得到投影矩阵，当面对新的测试样本时，只需执行简单的矩阵乘法即可得到样本在标签空间中的投影，因此在时间复杂度上具有较大优势。例如，最小二乘回归（least squares regression，LSR）[12]以一个onehot矩阵为回归目标，学习样本到标签的投影，LSR 存在解析解，因此求解速度很快。为了缓解one-hot 矩阵约束过于严格的问题，判别最小二乘回归（discriminative least squares regression，DLSR）[13]和重定目标最小二乘回归（retargeted least squares regression，ReLSR）[14]通过在标签空间中扩大不同类别间样本的距离，从而提高了模型的判别能力。

以上方法仅针对模型判别能力做出研究，然而数据中的噪声才是影响算法分类性能的最关键因素。噪声是数据中对分类任务产生负面影响的部分，它广泛存在于各种图像数据中，其分布与表现形式各不相同，例如光线的明暗变化会产生均值噪声，遮挡会产生稀疏噪声。因此，提高图像分类算法对噪声的处理能力是提高图像分类算法性能的关键。为使图像分类算法抵抗稀疏噪声干扰，鲁棒潜子空间学习（robust latent subspace learning，RLSL）[15]借助鲁棒主成分分析（robust principal component analysis，RPCA）[16]思想，将图像数据分解为一个低秩的数据矩阵和一个稀疏的噪声矩阵，然后使用不含稀疏噪声的数据矩阵进行分类，进而提高了分类性能。低秩判别最小二乘回归（low-rank discriminative least squares regression，LRDLSR）[17]在标签空间中引入低秩约束，抑制了标签空间中的部分噪声，使参与回归分类的数据更加“干净”。然而这些算法仍有很多不足，例如，RLSL 事先假设噪声属于稀疏分布，但是实际数据中噪声的类型和分布是未知的，因此假设噪声是稀疏的或稠密的并不合理，这种不合理的假设可能使模型错误地去除了有用的细节信息，但实际噪声却并未消除，从而影响分类性能；LRDLSR 在标签空间中引入低秩约束虽可在一定程度上抑制噪声影响，但是标签空间的数据已经过投影矩阵的处理，维数通常较低且极为稀疏，因此降噪效果不理想。

为提高算法对噪声鲁棒性，本文提出了一种基于潜子空间去噪的子空间学习（denoising latent subspace based subspace learning，DLSSL）模型，该模型放宽噪声类型和分布的假设，先对数据中的噪声进行处理，再将数据回归到标签空间中，最后对回归后的数据进行分类。将降噪与回归两个步骤设计到同一框架中，进行统一训练，使两个部分相互制约以进一步提高图像分类性能。该模型以标准DLSR 框架为基础，在原始视觉空间与标签空间中引入一个新的潜在子空间，使用欠完备自编码将数据压缩至潜在子空间中并尽可能地恢复，从而在潜在子空间中获取原始数据的高阶结构，然后使用潜在空间中的“干净”数据进行回归分类。此外根据文献[17]，在潜在子空间中引入组核范数约束，以抑制DLSR 框架中由于ϵ-拖动技术造成的类内样本距离增大的问题。最后，为两个投影矩阵分别引入不同的正则化参数，防止模型发生过拟合问题，模型架构图如图1 所示。

1 相关工作

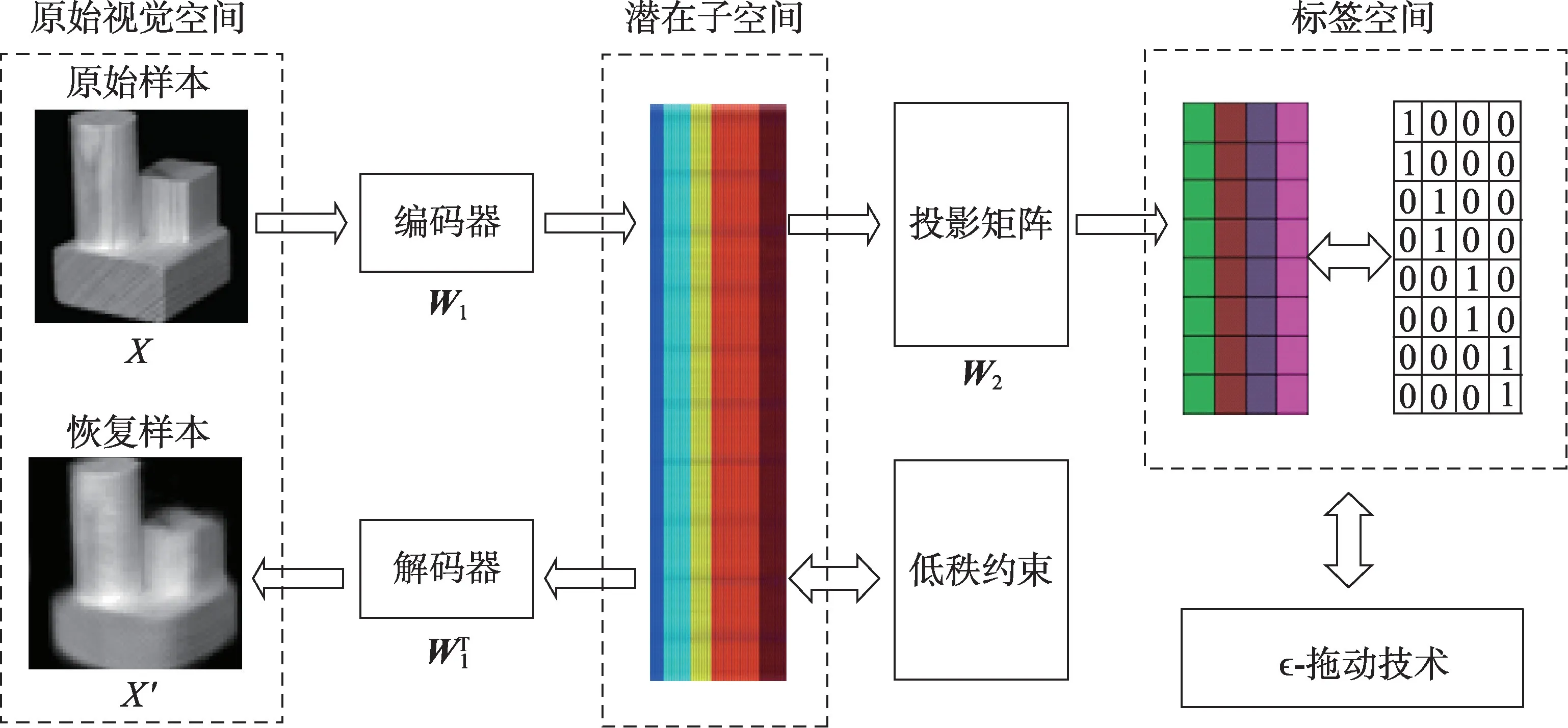
Fig.1 Framework of denoising latent subspace based subspace learning图1 基于潜子空间去噪子空间学习模型架构图

X=[X1,X2,…,Xc]=[x1,x2,…,xn]∈Rd×n为来自c个类别的n个训练样本，其中d表示训练样本的维数；H=[h1,h2,…,hn]∈Rc×n表示one-hot 标签矩阵，其中向量hi=[0,…,0,1,0,…,0]T∈Rc为样本xi的标签向量，若xi属于第j类，则hi的第j个元素值为1，其余元素值均为0，测试样本用y表示。

1.1 欠完备自编码器

自编码是一种经典的无监督机器学习方法，它的模型结构具有很大的灵活性，不同的模型结构有着完全不同的用途，例如稀疏自编码、变分自编码、栈式自编码等。本文的目标是通过自编码对数据进行降维并去除噪声，因此设置隐藏层的维数小于输出层的维数，即构建一个欠完备自编码。它尝试将数据压缩，并通过解压将输入尽可能地恢复到输出，从而学习到数据中最本质的高阶结构，实现类似主成分分析（principal component analysis，PCA）降维的效果。与PCA 不同的是，PCA 仅能处理符合高斯分布的数据，对尖锐噪声没有处理能力，欠完备自编码对任何分布的噪声都具有鲁棒性，其可以学习到一个比PCA 更为优秀的投影，从而更好地刻画数据的高阶结构。欠完备自编码可由如下目标函数来描述：

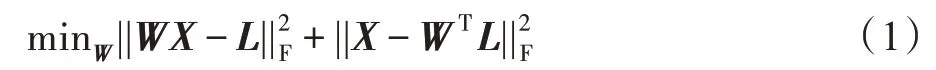
其中，W为投影矩阵，L∈Rr×n为训练集数据X在子空间中的投影，r表示子空间中的维数，||·||F表示矩阵的Frobenius范数。

通过对式（1）求导并令导数为0，可以得到一个标准的西尔维斯特方程[18]，通过求解此方程即可得到投影矩阵W。

1.2 判别最小二乘回归

DLSR 的主要思想是利用ϵ-拖动技术对LSR 中严格的one-hot 回归目标进行松弛化，从而扩大不同类别样本间的距离，使学习到的投影矩阵更具有鉴别性。DLSR 的优化目标可由如下优化函数来描述：

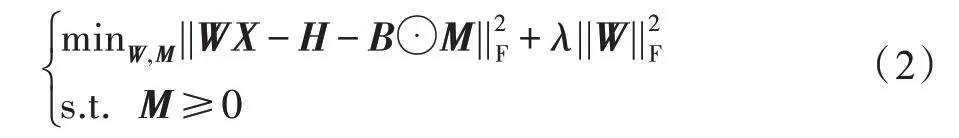
其中，M为ϵ-拖动矩阵，⊙为哈达玛积，定义为两矩阵对应元素相乘，λ为正则化参数，B为约束矩阵定义如下：

其中，矩阵下标i、j表示矩阵的第i行第j列的元素。

通过对式（2）使用交替方向乘子法（alternating direction method of multipliers，ADMM）[19]即可得到投影矩阵W。

2 潜子空间去噪的子空间学习

2.1 动机

图像数据通常包含各种冗余信息和噪声，这对图像分类产生了不利影响。对于数据中的冗余信息，可用主成分分析法进行消除。对于数据中的噪声，通常可以采用低秩分解方法，如RPCA 基于假设：噪声符合稀疏分布，因此利用矩阵分解即可将数据分解为一个噪声矩阵和一个低秩矩阵，然后利用不含稀疏噪声的低秩矩阵进行后续的图像分类。然而，数据中的关键信息通常也是稀疏的，如人脸胎记、汽车标志等，这就导致基于稀疏噪声假设的算法在降噪同时会损失数据中重要的关键信息，这对分类任务极为不利。

为说明这种情况，在COIL-20 数据集上进行了实验，利用RPCA 对COIL-20 数据库的数据进行处理，结果如图2 所示，其中第一行为原始数据，第二行为去除稀疏噪声后的数据，第三行是对应的稀疏噪声。显然由于不合理的噪声假设，致使许多关键细节信息丢失，如第8 列样本上的汉字“都”，这是所有类别所独有，但去除稀疏噪声后细节信息丢失。因此，可假设放宽噪声类型和分布以消除真正噪声，从而使回归分类环节使用的数据更“干净”。为此可以通过欠完备自编码将数据压缩至低维，再将其尽可能恢复，从而获取数据在低维空间的高阶特征。这种无监督的特征提取方法无需对数据分布或类型作出任何事先假设，因此对数据中包含的任意类型或分布的噪声都有很强的容忍能力。然而欠完备自编码对数据的压缩是有损的，如果直接将视觉空间中的数据压缩至标签空间，由于两个空间维度间的巨大差异和标签空间数据的稀疏性，将导致有效信息大量丢失，此时再将数据恢复至视觉空间将会产生严重的失真。因此引入一个潜在子空间作为视觉空间与标签空间的桥梁，其数据分布与视觉空间类似，维数介于二者之间，可以很好地保留数据中的信息，并通过压缩再恢复的方式降低数据中的噪声。基于此，本文结合DLSR 框架将欠完备自编码器与回归分类两个步骤合二为一，构建了一种联合优化模型，其目标函数如下：

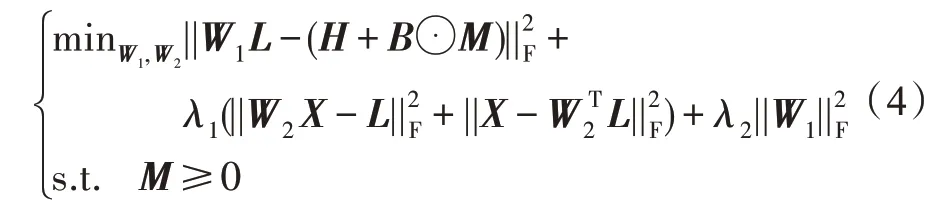
其中，W1为原始数据空间到潜在子空间的投影矩阵，W2为潜在子空间到标签空间的投影矩阵。

由于测试样本与训练样本并不属于完全相同的样本空间，难免发生过拟合现象，需要为用于降噪的投影矩阵W2添加额外的正则化参数用于防止过拟合，此时的模型定义如下最优化函数表示：

由于DLSR 中ϵ-拖动技术的使用难免会增大样本空间同类样本间的距离[17]，采用与LRDLSR 中相同的处理手段，为模型引入组核范数约束，用于抑制类间样本距离增大问题，提出一种基于潜子空间去噪的子空间学习（denoising latent space based subspace learning，DLSSL）图像分类算法，将降噪与分类两个步骤合二为一，构建了一种全新的联合优化模型，模型的定义如下：

Fig.2 Part of samples processed by RPCA on COIL-20 dataset图2 COIL-20 数据集经过RPCA 处理过后的部分样本

2.2 求解步骤

为便于求解该模型，在模型中添加Q和T两个辅助变量，接着使用ADMM 算法进行求解，求解的目标函数为：

其中，R1、R2为拉格朗日乘子，μ＞0 是惩罚参数，接下来将按顺序迭代求解每一个参数。

固定其余参数，更新P：

其中，Tij、Bij、Mij表示T、B、M矩阵的第i行第j列，考虑到M矩阵具有一个非负约束，因此可以获得如下等式：

求解式（6）可获得两个投影矩阵W1、W2，对于任何测试样本y，其在标签空间中可表示为W1W2y，随后使用最近邻分类器[8]对标签空间中的数据进行分类。

算法的整个流程如算法1 所示。

算法1潜子空间去噪的子空间学习算法流程

输入：标准化过后的训练集X，one-hot 矩阵H，最大迭代次数T，超参数λ1、λ2、λ3、λ4、λ5、r。

初始化：M=Q=P=L=T=0，W1=W2=1，μmax=107，R1=R2=0，μ=10-5，ρ=1.1，ϵ=10-4。

循环变量从1 →T开始循环：

根据式（12）更新P；

根据式（13）更新T；

根据式（17）更新Q；

根据式（21）更新M；

根据式（25）更新L；

根据式（29）更新W1；

根据式（33）更新W2；

根据式（34）更新拉格朗日乘子R1、R2；

根据式（35）更新惩罚参数μ；

如果||Pk-Qk||∞＜ϵ且||Pk-Tk||∞＜ϵ

跳出循环；

结束如果；

结束循环；

输出：投影矩阵W1、W2。

2.3 时间复杂度及收敛性验证

DLSSL 模型的主要耗时步骤是：（1）式（13）中的奇异值分解，其时间复杂度为O(n3)；（2）式（33）中求解西尔维斯特方程，其时间复杂度为O(d3)。其他步骤是简单的矩阵加、减、乘，耗时可以忽略不计。因此采用文献[17]类似的处理方法，使用以上两个步骤的时间复杂度来近似表示DLSSL 模型的时间复杂度，为O(t(n3+d3))，其中t表示迭代次数。

ADMM 算法在求解2-block 问题时，可保证解一定收敛，然而本文算法包含多个变量，是一个n-block问题，ADMM 算法不能保证其一定收敛[21]。虽然尚没有理论严格证明在何种情况下ADMM 算法求解的n-block 问题收敛，但多数相关类似算法在实际使用时可以很好地收敛[15,17,22-23]。

为了进一步验证本文算法实际的收敛情况，在AR、CMU PIE、COIL-20 和Finger Knuckle Print（FKP）数据集上进行收敛性实验，实验结果如图3 所示。不同数据集下的收敛速度有所不同，但经过20 次迭代，所有的数据集均能很好地收敛，目标函数值与准确率都趋于稳定，这验证了本文算法具有很好的收敛性。

3 实验结果与分析

本文所有算法在以Windows10 系统环境下的Matlab（2020b）为软件平台，采用AMD Ryzen 7 2700 3.20 GHz CPU、NVIDIA RTX3080 GPU 和32 GB 内存，其中算法中求逆矩阵、奇异值分解等耗时运算采用GPU 计算。本文算法将与NNC、SRC、LRC、CRC、ProCRC、DLSR、ReLSR、RLRLR、RLSL、LRDLSR、VGG16（Visual Geometry Group16）[24]、ResNet50（Residual Network50）[25]、MobileNet[26]、Xception[27]进行比较。实验数据均采用PCA 进行预处理以降低维数（深度方法除外），实验重复8 次记录平均准确率与标准差。

3.1 人脸识别实验

Fig.3 Convergence curves and accuracy of proposed method图3 本文算法目标函数的收敛曲线与准确率

人脸样本容易受到不同光线、角度、面部表情、遮挡等干扰因素的影响，导致类内差异性较大，而不同类别通常具有较大的相似性，因此图像分类中的人脸分类对算法鲁棒性提出较高要求，需要算法尽可能缩小类内距离，并使不同类别样本间的距离尽可能大。算法将在如下人脸数据集上进行实验：

AR 数据集[28]：包含120 位志愿者，每人26 幅，包含不同表情、光照、角度、遮挡等情况，26 幅图像分两部分，前后各13 幅，间隔14 天采集，共计3 120 幅，部分样本数据如图4 所示。为平衡男女比例，从AR 数据集中抽取包含50 名男性与50 名女性的一个子集，并将样本下采样至165×120 像素。随机选取每一类样本中的3、4、5、6 个样本作为训练集样本，其余样本为测试集样本，结果如表1 所示。

Extended Yale B 数据集[29]：包含38 人，每人有64幅，包括不同的表情和姿势，总共有2 432 幅图片。所有图片都经过灰度化预处理，并且采样为96×84 像素，部分样本数据如图5 所示。实验随机选取每一类样本中的10、15、20、25 个样本作为训练集样本，其余样本为测试集样本，结果如表2 所示。

Fig.4 Some images from AR dataset图4 AR 数据集中的部分样本

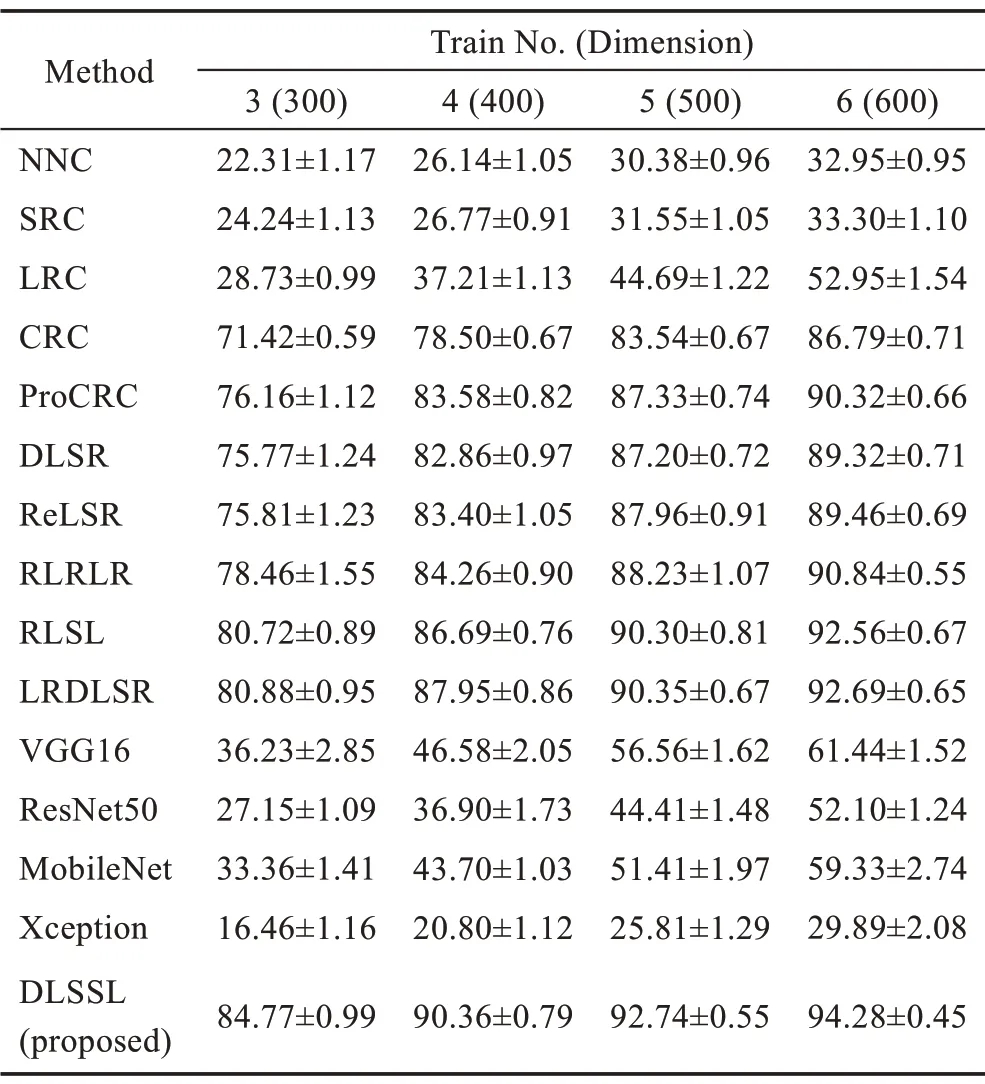
Table 1 Recognition accuracy(mean±std)of different methods on AR dataset表1 AR 数据集上不同方法的识别率（平均值±标准差）%

CMU PIE 数据集[30]：包含68人，共41 368幅图像，包含不同角度、光线、表情的样本，其中含有5 个不同光照、表情的接近正脸角度的子数据集（C05、C07、C09、C27 和C29），部分样本数据如图6 所示。实验选取明暗变化较明显的C27 进行实验，C27 包含68 人，每人24 幅，共1 632 幅图像。实验时将样本下采样至64×64 像素，并随机选取每一类样本中的5、10、15、20 个样本作为训练样本，其余作为测试样本，结果如表3 所示。

Table 2 Recognition accuracy(mean±std)of different methods on Extended Yale B dataset表2 Extended Yale B 数据集上不同方法的识别率（平均值±标准差）%

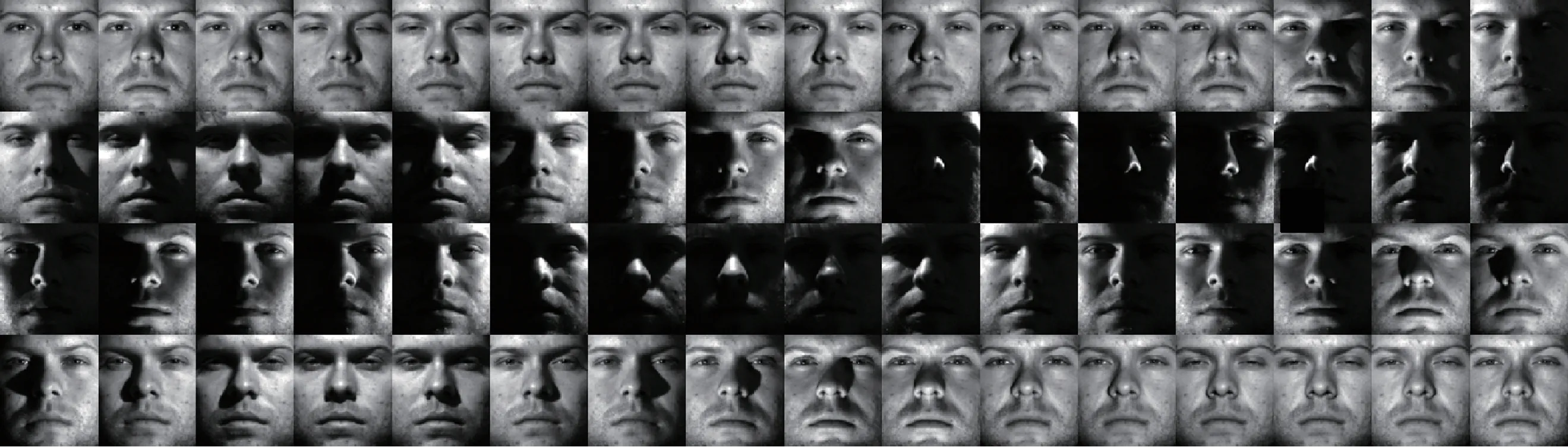
Fig.5 Some images from Extended Yale B dataset图5 Extended Yale B 数据集中的部分样本

Fig.6 Some images from CMU PIE dataset图6 CMU PIE 数据集中的部分样本

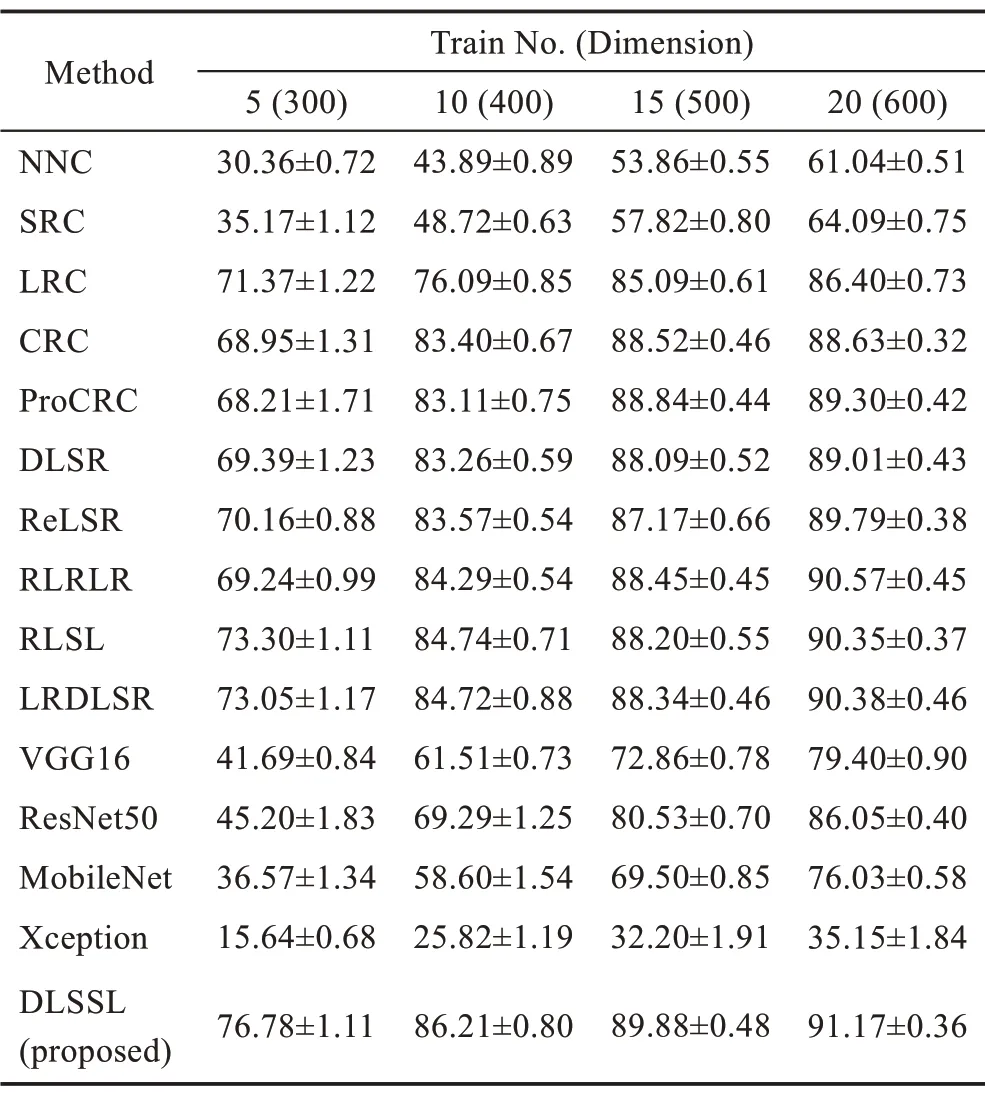
Table 3 Recognition accuracy(mean±std)of different methods on CMU PIE dataset表3 CMU PIE 数据集上不同方法的识别率（平均值±标准差）%

人脸识别实验中样本包含大量噪声，经典的NNC算法没有噪声抵抗能力，因此精度不理想；SRC、LRC算法基于稀疏表示理论，对样本中的明暗噪声具有一定的鲁棒性，因此识别率高于NNC 算法，尤其在Extended Yale B 数据集（多为不同光照条件下的人脸样本）的结果取得了大幅领先；CRC 与ProCRC 利用样本间的协同性，进一步提高算法对于明暗噪声的鲁棒性；DLSR、ReLSR、RLRLR、RLSL 和LRDLSR 基于线性回归算法，这些算法在训练阶段将学习到的投影矩阵用于新样本识别，对样本噪声具有较强的抵抗能力，因此结果明显优于NNC、SRC、LRC、CRC和ProCRC 算法，其中RLSL 和LRDLSR 算法在识别率上小幅领先DLSR、ReLSR 和RLRLR 算法，这是由于RLSL考虑了样本的稀疏噪声，LRDLSR利用核范数约束抑制了标签空间中的噪声。VGG16、ResNet50、MobileNet 和Xception 是基于深度卷积网络的方法，这些方法具有海量的参数，能较好地拟合各种非线性数据，然而在人脸识别实验中，由于样本数量较少，致使学习到的权重参数发生了严重的过拟合现象，分类精度严重下降。本文算法在各种实验设置情况下均大幅领先其他算法，这是由于本文算法更加合理地考虑了噪声的类型与分布，不再对噪声施加不合理的先验假设，潜在空间中的数据更加准确，且包含的有效信息更多，对噪声具有更强的鲁棒性。

3.2 生物指纹识别实验

不同于图像分类中的人脸图像，生物指纹特征图像的获取难度相对较高，大多数情况下每类样本数量较少，这是一个典型的小样本学习任务，在处理这种任务时，算法可利用的信息体量较小，因此少量噪声就会对算法性能造成严重影响。算法将在以下生物指纹图像数据集上进行实验：

PolyU Palmprint数据集[31]：包含400 个不同手掌，每类20 个样本，共8 000 个样本。所有图像都经过灰度化预处理，并调整为64×64 像素，部分数据样本如图7 所示。实验选取100 类，每类6 个，共计600 个样本构成一个子数据集。随机选取每类样本中的2、3个样本作为训练集，其余样本作为测试集（每种训练集下仅随机抽取一次样本），使用PCA 对原始数据降维，绘制不同维度下平均识别率的曲线，如图8 所示，多次实验中各算法的最高识别率如表4 所示。

Fig.7 Some images from PolyU Palmprint dataset图7 PolyU Palmprint数据集中的部分样本

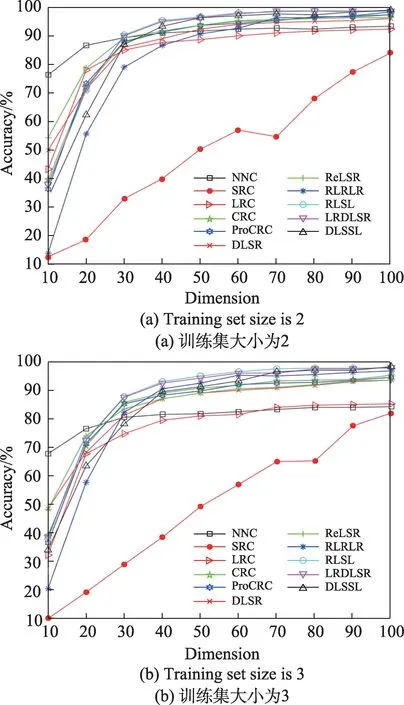
Fig.8 Accuracy curves of different methods with varied dimensions on PolyU Palmprint dataset图8 PolyU Palmprint数据集上不同维度与准确率曲线

Finger-Knuckle Print 指关节纹数据集[32]：包含660 个不同手指，每类12 个样本，共7 920 个样本。所有图像都经过灰度化预处理，并调整为55×110 像素，Finger-Knuckle Print 数据集的部分样本如图9 所示。选取100 类，每类12 个，共计1 200 个样本构成一个子数据集。随机选取每类样本中的2、3 个样本作为训练集，其余样本作为测试集（每种训练集下仅随机抽取一次样本），使用PCA 对原始数据降维，绘制不同维度下平均识别率的曲线，如图10 所示，多次实验中最高准确率如表5 所示。

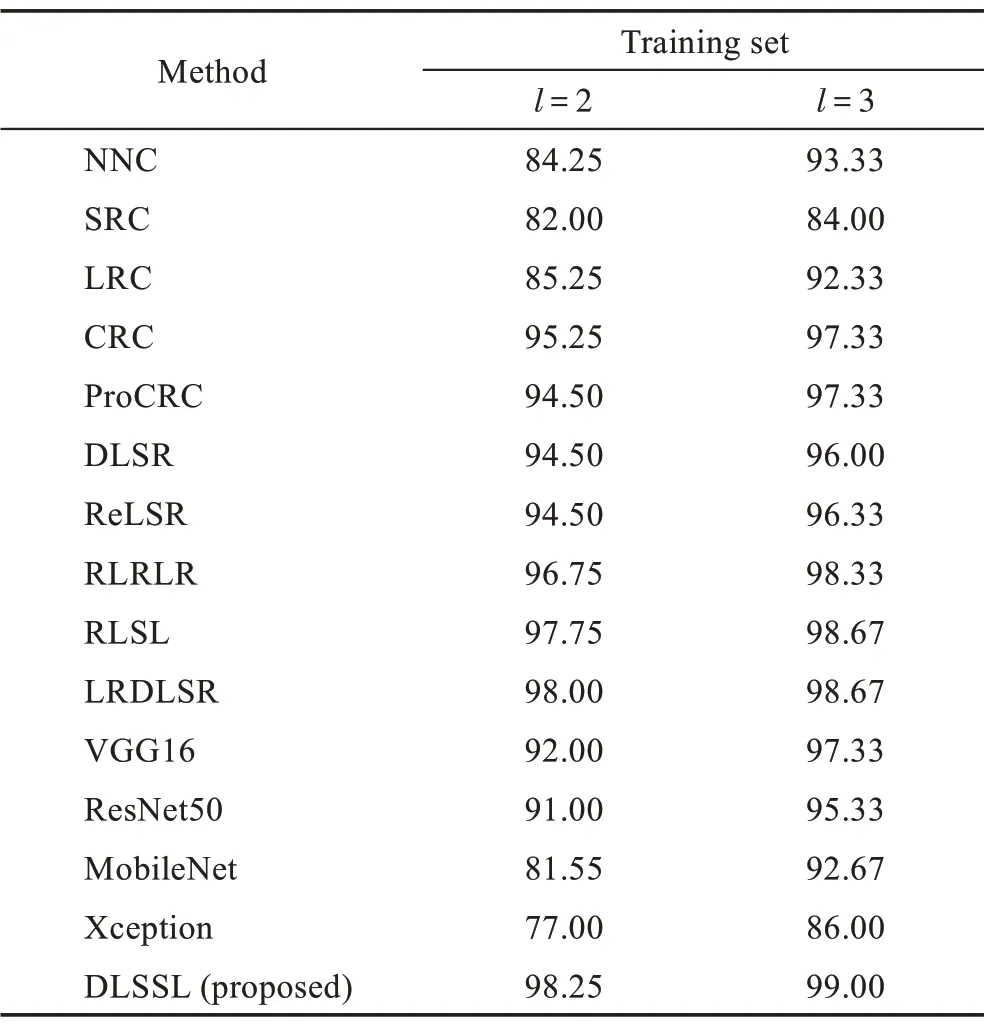
Table 4 Accuracy on PolyU Palmprint dataset表4 PolyU Palmprint数据集上的识别率 %

Fig.9 Some images from FKP dataset图9 FKP 数据集中的部分样本

生物特征样本中由于样本采集环境相对统一样本中的噪声较小，各算法识别率差距小于人脸识别实验。识别率方面，基于线性回归算法与基于协同表示算法各有优劣，基于稀疏表示算法相对较差，基于深度学习的方法仍然受限于数据量，性能表现不佳，总体呈现与人脸识别实验相似规律。其中RLRLR 算法在Finger-Knuckle Print 数据集上，在训练集为2 时性能不理想，这是因为RLRLR 利用了样本的近邻关系优化数据分布，然而本部分实验设置中的训练样本规模较小，因此严重影响了其性能。从图8 和图10可以发现，随着样本维数增加，各算法识别率逐渐提高，当样本维数超过40 时，各算法识别率基本稳定，本文算法在低维度时性能优势不大，这是因为欠完备自编码作为一种无监督的特征提取方式在数据维度较小时不能很好地刻画数据特征，使得提取的特征失真从而影响识别率。从表4 和表5 可以发现，随着样本维数逐渐变大时这种缺点将不复存在，因此本文算法取得的最高识别率领先于其他各算法。

Fig.10 Accuracy curves of different methods with varied dimensions on FKP dataset图10 FKP 数据集上不同维度与准确率曲线

3.3 物体识别实验

物体识别和人脸识别、生物特征识别具有很大的差异，这是由于数据集中不同类别的样本差异性很大，从而导致某些基于样本重建算法无法利用其他类别数据的信息帮助提高样本的重建质量。此外由于物体形状不同，样本角度和光照变化很大，使得类内差异急剧增大，给分类带来了更大的困难。算法将在如下数据集上进行物体识别实验：

COIL-20 数据集[33]：包含20 个不同物体，每类72个样本，共1 440 个样本。所有图像都经过灰度化预处理，并调整为32×32 像素，COIL-20 数据集上的部分样本如图11 所示。实验前随机选取每类样本中的5 个样本构建训练集，使用同一个训练集对比各算法的性能情况，结果如表6 所示。图12 展示了标签其混淆矩阵。图13 展示了标签空间中数据的t 分布随机邻域嵌入（t-distributed stochastic neighbor embedding，t-SNE）可视化结果。

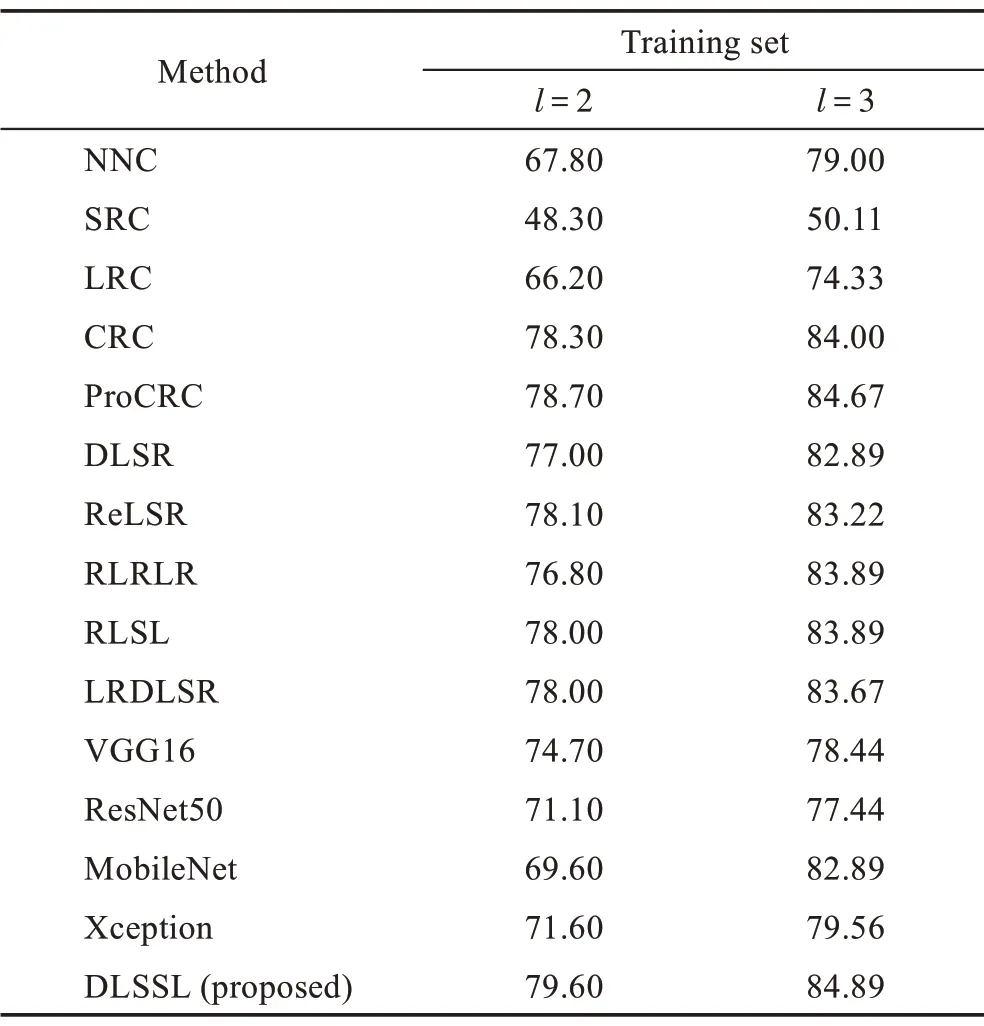
Table 5 Accuracy on FKP dataset表5 FKP 数据集上的识别率 %

Fig.11 Some images from COIL-20 dataset图11 COIL-20 数据集中的部分样本

Table 6 Accuracy on COIL-20 dataset表6 COIL-20 数据集上的识别率 %

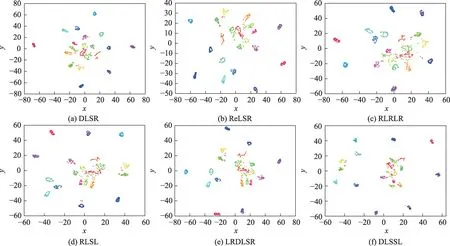
Fig.13 t-SNE visualization results on COIL-20 dataset图13 COIL-20 数据集上t-SNE 的可视化结果

从图13 各种基于线性回归算法的t-SNE 可视化结果可以发现，多数同类样本聚合成一点，但仍然存在许多离散点，这些离散点是由于样本噪声造成的较难分类的样本。由于没有考虑噪声处理，DLSR、ReLSR 和RLRLR 的可视化结果中离散点相对较多，RLSL 和LRDLSR 算法考虑了样本噪声，因此离散点相对较少，本文DLSSL 算法的可视化结果中类内样本聚集更为紧密，类间距离相对较大，且杂乱分布的点较少，这表明DLSSL 模型对噪声具有较强的鲁棒性，能够较好地保留数据的基本结构。图12 中的混淆矩阵极为稀疏，说明DLSSL 算法也具有很强的判别能力。从表6 可以更加直观地发现DLSSL 在多种算法中取得了最高的识别率。

3.4 深度特征识别实验

不同于上述3 类数据集，深度特征来源于深度神经网络的处理，具有高度的抽象性，这种抽象的数据形式更加精炼，所含的噪声更少；同时由于数据的高度抽象，可能会使数据丢失原有的流形结构，使一些基于距离度量的算法性能下降，从而使某些基于几何、纹理等特征识别的算法彻底失效。为验证各算法在面对深度特征时的有效性，使用了两种不同的深度神经网络用于特征提取（VGG16 和ResNet50），分别提取如下两个图像数据集的特征：

FERET 数据集[34]：包含10 000 多个不同姿态和照明条件下的图像样本。本部分实验选择一个200 人的子集，每人7 幅，共计1 400 幅图片，所有图像都经过灰度化预处理，并调整为80×80 像素。此部分随机选取每一类样本中的5 个样本作为训练样本，其余为测试样本，FERET 数据集上的部分样本如图14 所示。

Fig.14 Some images from FERET dataset图14 FERET 数据集中的部分样本

COIL-20 数据集：随机选取每一类样本中的5 个样本作为训练样本，其余为测试样本。比较各算法在处理非深度特征、VGG16 和ResNet50 深度特征数据时的性能，实验结果如表7 所示。

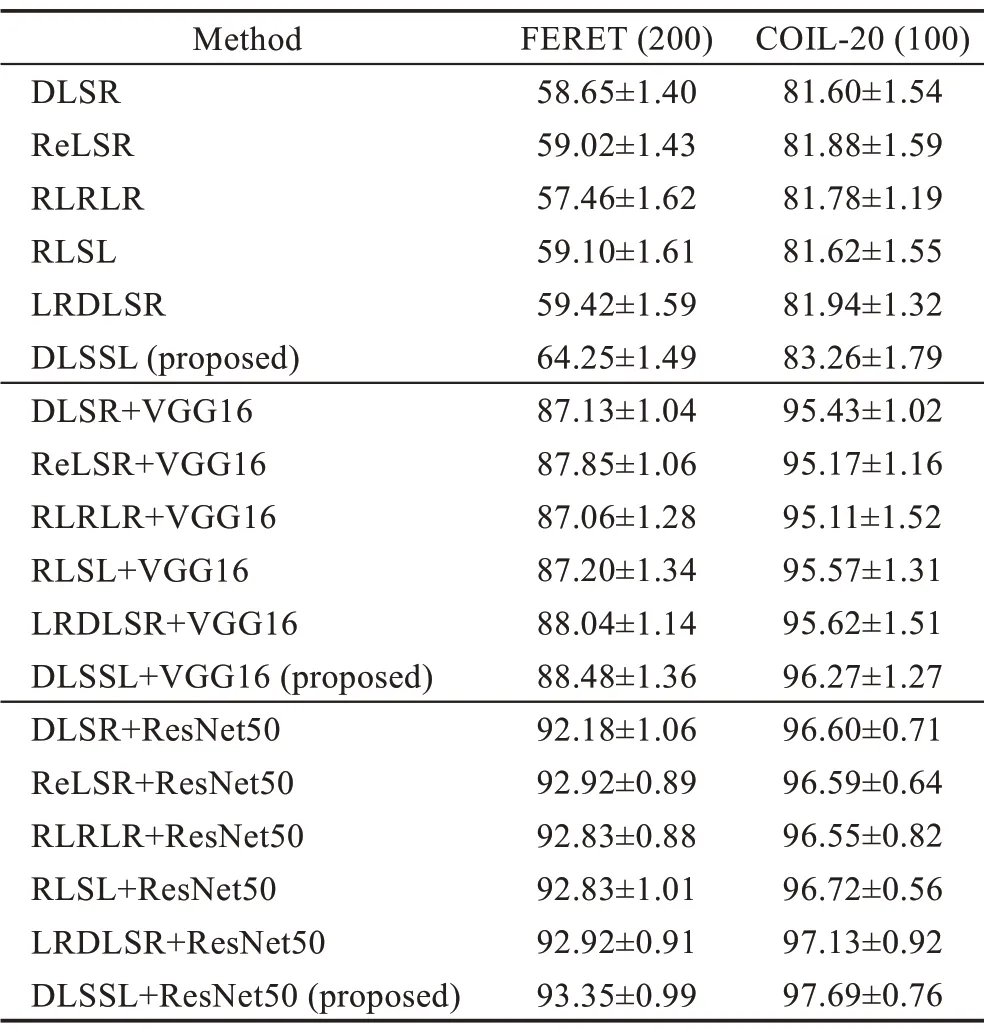
Table 7 Deep features accuracy(mean±std)表7 深度特征识别率（平均值±标准差）%

经过深度神经网络提取的特征数据中所含的噪声大幅降低，各算法性能得到显著提高。面对如此高度抽象数据，DLSSL 模型仍然领先于其他基于线性回归算法并取得最好效果，这说明DLSSL模型不仅在处理噪声数据方面具有优势，而且在面对几乎没有噪声数据时，也能更好地利用样本信息，可以学习一个类内差异更小、类间判别能力更强的子空间投影。

3.5 参数敏感性实验

DLSSL 模型有6 个重要的超参数λ1、λ2、λ3、λ4、λ5、r，其中λ1、λ2是平衡参数，用于平衡从原始空间到潜在空间到标签空间的变换权重，λ3、λ4是防止过拟合的正则化参数，λ5是类的低秩目标学习项，文献[17]中已证明此参数对实验结果影响较小，后续实验中将其设置为10，参数r是潜在空间的维数。

首先设置超参数λ1=λ2=1E+0，λ3=λ4=5E-5，λ5=1E+1，然后验证在不同潜在子空间维度r下的识别率，结果如图15 所示。随着潜在子空间维数的增加，算法的性能逐渐提升，在r＞2c后趋于稳定。由于r的大小决定潜在子空间维数的大小，维数越大，算法的时间与空间复杂度越高，因此选择r=2c；其次固定超参数r=2c，λ3=5E-5，λ4=5E-5，然后验证不同参数λ1，λ2∈{1E+0,5E-1,1E-1,5E-2,1E-2,5E-3,1E-3,5E-4,1E-4,5E-5} 对模型性能的影响，不同λ1和λ2在AR 与CMU PIE 数据集的识别率如图16 所示。从图中可以发现，当λ1=λ2=1E+0 时模型的性能较好，这是由于这两个空间中的转换同等重要；最后固定超参数r=2c，λ3=5E-5，λ4=5E-5，然后验证不同参数λ1，λ2∈{1E+0,5E-1,1E-1,5E-2,1E-2,5E-3,1E-3,5E-4,1E-4,5E-5}对模型性能的影响，不同λ3和λ4在AR 与CMU PIE数据集的识别率如图17 所示。可以发现λ3的选取对实验结果影响较大，λ4对识别率影响较小。综上所述，本文算法虽包含众多参数，但除λ3外其余参数对结果影响较小，不同数据集上参数选取基本相似，因此通常情况下默认λ1=λ2=1E+0，λ4=5E-5，λ5=1E+1，r=2c，仅需要选取λ3∈[1E-1,1E-5]。

4 结束语

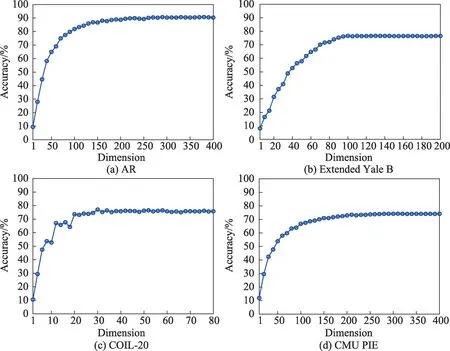
Fig.15 Accuracy of DLSSL for different parameters r on each dataset图15 各数据集上不同参数r 时DLSSL 的识别率曲线

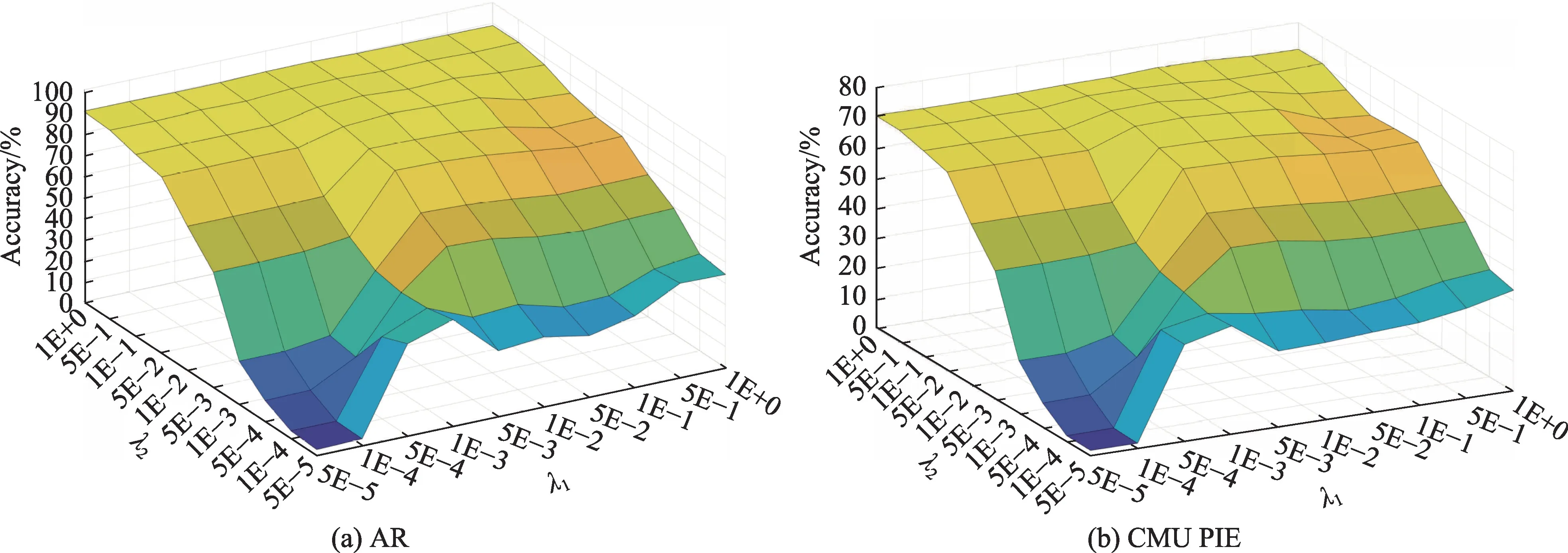
Fig.16 Accuracy of different λ1 and λ2 on AR and CMU PIE datasets图16 不同λ1 和λ2 在AR 与CMU PIE 数据集上的识别率

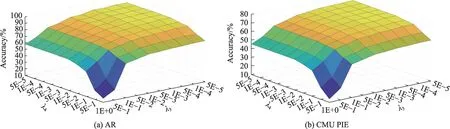
Fig.17 Accuracy of different λ3 and λ4 on AR and CMU PIE datasets图17 不同λ3 和λ4 在AR 与CMU PIE 数据集上的识别率

本文分析了现有几种基于子空间学习的图像识别算法，找出了其在噪声类型与分布假设上的不合理之处，提出了一种基于潜子空间去噪的子空间学习（DLSSL）图像分类算法。该方法以DLSR 框架为基础，在原有的视觉空间与标签空间中引入了潜在子空间，结合欠完备自编码器提取数据中的高阶特征，再利用数据的高阶特征进行回归分类，辅助以组核范数约束，优化类内样本间距离。在人脸识别、生物特征识别、物体识别、深度特征识别四种不同领域的图像数据集上设计了实验，实验结果表明所提算法对数据中存在的各种类型与分布的噪声都具有较强的鲁棒性，所构造的子空间判别性更好，分类性能优于现有相关算法。本文算法对传统线性回归框架进行了较大幅度的修改，使其具有较好的灵活性与扩展性，未来的工作将利用这种优势，从多角度发掘数据的潜在价值，优化数据的表现形式，开发出一种更为普适的图像分类工具。