单步划分融合多视图子空间聚类算法
2021-12-13蔡志平
张 培,祝 恩,蔡志平
国防科技大学 计算机学院,长沙 410073
传统的聚类方法通过计算数据特征之间的相似度来对样本进行聚类。然而仅使用单一的特征可能会存在一定的偏差或不足。随着信息技术、数据挖掘技术等的发展,数据可以被不同类型的特征描述。例如相同语义使用多语言形式表示[1];生物特征识别中可以使用人脸、指纹、掌纹以及虹膜等特征来唯一地标识一个人;网页包含文本、链接以及视频等多种模态的数据。这种使用不同的特征来描述的数据称为多视图数据。多视图数据不仅包含每个视图下特定信息,也包含视图之间互相补充的信息[2]。使用多视图数据进行聚类可以充分发挥各视图的优势,规避各自的局限,从而获得更好的聚类性能。
现有的多视图聚类算法可以被分为四类:直接连接的方法、多核聚类算法[3]、基于图的多视图聚类算法[4]以及多视图子空间聚类算法[5]。多视图子空间聚类算法通常包含基于矩阵分解的方法和基于子空间的方法。其中基于矩阵分解的方法[6-7]旨在从所有视图学习一个统一的特征表示。而基于自表达的多视图子空间聚类算法[8-9]在很多应用中展现了有效性和鲁棒性。其关键问题在于学习统一的子空间表示,从而揭示多个视图下理想的一致的聚类结构。现有的多视图子空间聚类方法大多是将多个图或表示矩阵融合成一致的图或表示矩阵,即在相似度级别上融合多视图信息。如文献[10]通过执行矩阵分解得到一致的稀疏子空间表示。类似的,文献[11]得到低秩和稀疏约束下的一致相似度矩阵。也有一些方法首先学习一个潜在表示,然后从潜在空间进行子空间聚类。文献[12]通过最大化视图之间的独立性来编码视图之间的互补信息,进而得到一致的表示。与之类似的是文献[13],假设所有的视图都源于一个潜在表示,通过对潜在表示进行子空间聚类得到子空间表示。
尽管这些方法在不同的场景下都取得了极大的成功,但仍存在以下问题:原始数据中通常包含噪声和一些冗余的信息,因此直接将从原始数据中学习一致的相似图矩阵或者表示矩阵融合可能会影响最终的聚类性能。此外,现有的方法大多为两阶段,即先进行相似度学习再应用谱聚类或者其他离散化方法得到最终的聚类结果。这样将表示学习的过程与最终的聚类任务分离的方法会导致学到并不是最适合聚类任务的表示,从而无法得到最优的聚类性能。
本文提出了一种单步划分融合多视图子空间聚类算法(one-stage partition-fusion multi-view subspace clustering,OP-MVSC),将表示学习、划分融合以及聚类过程集成在一个框架中。在这个框架中,联合优化每个视图的相似性矩阵、划分矩阵以及聚类标签。具体来说,本文首先在每个视图上建立各自的子空间表示。不同的视图之间聚类结构应该是类似的,基于这一假设,将每个视图的划分矩阵融合为一致的划分矩阵。这种划分级别的融合可以避免相似度级别融合中引入原始数据中的噪声和冗余。此外,通过对一致的划分施以旋转矩阵可以直接得到聚类结果,避免使用额外的谱聚类或者其他离散化方法获得聚类标签。通过表示学习、划分融合、谱旋转这三个子过程的交互,它们之间互相促进,从而获得更好的聚类结果。除此之外,本文提出一种有效的算法来解决由此产生的优化问题,并在四个广泛使用的多视图数据集上与一些先进的方法进行了对比实验,证明了所提方法的有效性和先进性。
1 相关工作
1.1 符号与定义
对于矩阵A,Ai,:表示第i行,Ai,j表示矩阵A第i行、第j列处的元素。矩阵A的Frobenius 范数表示为||A||F,向量的2 范数表示为||Ai,:||2。矩阵的迹、转置分别表示为tr(A)及AT。
定义一个有m个视图、n个样本的数据集为A=[A1,A2,…,Am]∈Rd×n,其中d=表示第v个视图中特征的维度。第v个视图的数据则表示为。此外使用粗体的1 表示元素全为1 的列向量,使用Ik表示k×k维的单位矩阵。
1.2 多视图子空间聚类相关工作
对于一组数据来说,其数据点通常分布在潜在的低维子空间中而不是均匀分布在整个空间[10]。因此数据点可以通过低维的子空间来表示。在获得数据的子空间结构后,可以在子空间中进行聚类来代替在整个空间中聚类。给定n个样本的数据A={a1,a2,…,an}∈Rd×n,其中某个样本ai可以使用与它位于同一个子空间的其他样本的线性组合表示。选取A中的d个样本构成字典D,那么A中每一个样本都可以表示为D中数据点的线性组合。随着自表达性质[14]的兴起,可以使用整个数据矩阵作为字典来表示数据本身,如式(1)所示:
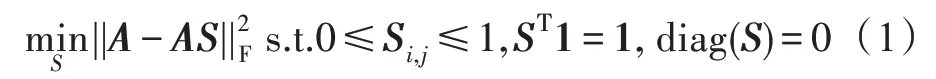
其中,S={s1,s2,…,sn}∈Rn×n是数据点的线性组合系数矩阵,称为子空间表示,每个si是原始数据ai的子空间表示。约束diag(S)=0 要求S的对角线元素为0,避免数据点由自己来表示。扩展到多视图场景,范式如下:
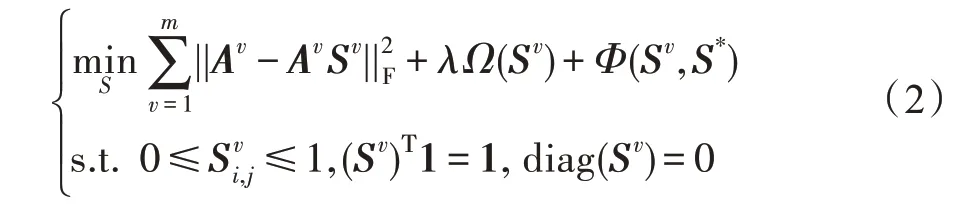
其中,Av表示第v个视图的数据,Sv表示第v个视图的子空间表示。Ω(·)为某种正则化函数,Φ(·)为某种可将多个视图的子空间表示融合为一致表示的策略。λ>0 是平衡参数。使用不同的正则化函数和不同的一致策略,组成了不同的多视图子空间聚类方法。其中大部分方法在获得一致的表示S*后,通过W=1/2(|S*|+|S*T|)得到相似度矩阵,然后进行谱分解得到划分矩阵F,再对F使用某种聚类算法(通常是K-means)得到最终的聚类标签。
然而真实世界的数据会有噪声、异常点或冗余信息,这可能导致相似度矩阵质量较差,直接融合这样充满噪声和冗余的多视图相似信息会导致较差的聚类结果。且后续得到聚类标签的过程与前面的相似度学习的过程分离,这也导致了无法得到最优的聚类性能。为了解决这些问题,本文提出一种新的单步划分融合多视图子空间聚类算法。
2 算法
本章介绍单步划分融合多视图子空间聚类方法,并给出相应的优化算法。
2.1 单步划分融合多视图子空间聚类算法
根据前文介绍的多视图子空间聚类范式(2),可以得到每个视图对应的子空间表示:

一个理想相似度矩阵中应具有如下性质:相似度矩阵中连通分量的个数等于聚类的簇的个数。根据文献[15]可知,相似度矩阵中连通分量的个数等于对应拉普拉斯矩阵中零特征值的重数。因此,希望相似度矩阵对应的拉普拉斯矩阵的零特征值数等于聚类的簇的个数k,即rank(Lv)=n-k。自然地,希望将这个秩约束加入到式(3)中,使得Sv具有所希望的理想性质。然而直接使用rank(Lv)=n-k的秩约束会使得该优化问题难以解决。根据Ky Fan 定理[16],可以得到=min tr((Fv)TLvFv),其中σi(Lv)是Lv的第i小的特征值。很明显,Lv的前k小的特征值均为0,即=0,将使得Lv的秩为n-k。因此,问题可以自然转化为如下形式:
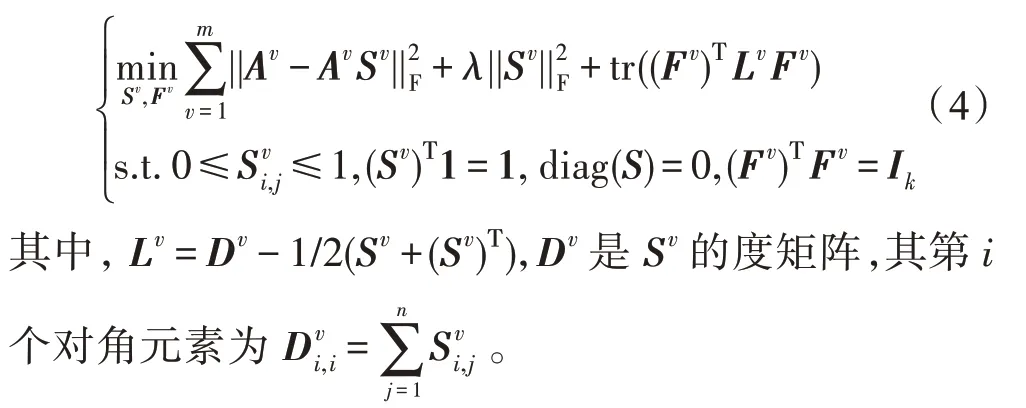
在式(4)中,每个视图可以得到各自的划分矩阵。在多视图聚类中,基于不同视图之间的聚类结构应该是类似的假设,即无论在哪个视图,相似的样本都应该被聚在同一个簇中。因此将每个视图的划分Fv对齐,形式化如下:
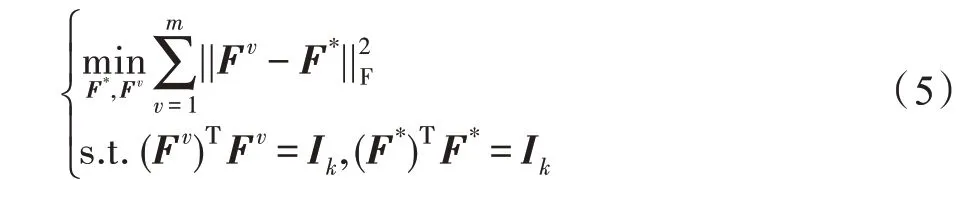
为了建立划分矩阵与最后的聚类标签之间的联系,引入旋转矩阵P∈Rk×k:
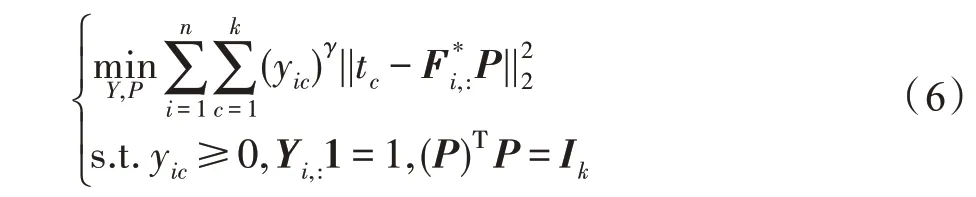
式中,γ为模糊系数。tc为1×k维的向量,其中只有第c个元素为1其余元素为0。为F*的第i行,对应第i个样本的一致表示。yic表示第i个样本属于第c个簇的概率。P则建立了标签Y和一致表示F*之间合理的关系。如果样本i在位置c显示出突出的结构,则对应yic有一个较大的概率值,表示样本i较大概率属于第c个簇。
将式(4)(5)(6)整合在一起,可以得到整个框架:

通过这种方式,相似度矩阵、一致划分及标签矩阵得以在一个框架中联合优化,并且这三个过程可以互相促进,从而获得更好的聚类结果。
2.2 优化过程
2.2.1 固定Fv、F*、P、Y,优化Sv
忽略无关项,目标函数的优化式可转化为:

由于每个视图都需要进行子空间表示的建立,可以对每个视图的Sv分别进行优化。将Sv按列展开可以得到如下向量形式:

其中,Qi,j=||Fi,:-Fj,:||2,Fi,:为对应F的第i行。对S:,i求导并令导数为0 可以得到S:,i的闭式解:
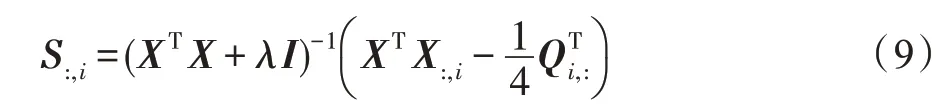
2.2.2 固定Sv、Fv、P、Y,优化F*
去掉其他无关项,关于F*的优化式可转化为:


2.2.3 固定Sv、F*、P、Y,优化Fv
关于Fv的优化式可以转化为:

2.2.4 固定Sv、Fv、F*、Y,优化P
忽略其他无关项,P的优化式可以转化为:

2.2.5 固定Sv、Fv、F*、P,优化Y
忽略其他无关项,关于Y的优化可以转化为:
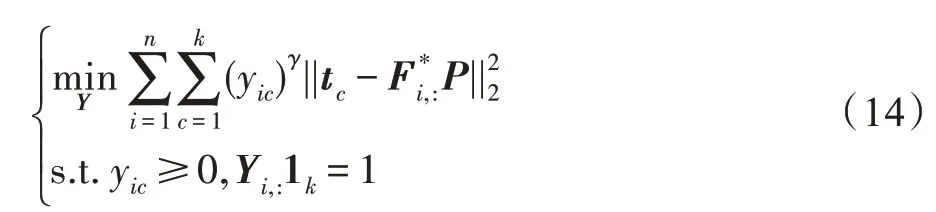
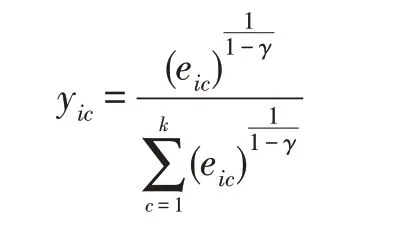
2.3 时间复杂性分析
整个算法流程如算法2 所示。在整个优化过程中,算法OP-MVSC 的计算复杂性可以分为相似图构建、划分融合以及谱旋转三个子阶段。其对应的时间复杂度分别为O(mn3+(m+1)nk3)、O(k3)以及O(nk2)。因此,算法2 的整体时间复杂度为O(T(mn3+mnk3+k3)),其中T为迭代次数。
算法2OP-MVSC
输入:具有m个视图的多视图数据,聚类个数k,超参数λ、γ。
输出:聚类标签矩阵Y。
初始化:初始化Fv,随机正交初始化F*,初始化P为k×k维的单位矩阵,初始化Y为每行只有一个位置为1 其余为0 的n×k维的矩阵
1.重复执行
2.通过式(9)来优化Sv
3.通过解式(10)来优化F*
4.通过解式(12)来优化Fv
5.通过解式(13)来优化P
6.通过解式(14)来优化Y
7.直至算法收敛
8.返回聚类标签矩阵Y
3 实验及结果分析
3.1 数据集介绍
本文在4 个广泛使用的公开数据集上进行了实验。如表1 所示,Wikipedia Articles 是一个广泛使用的跨模检索数据集,包含属于10 个类的693 个样本。将从图像中提取128 维的SIFT 特征和从文本的隐含狄利克雷分布模型中提取的10 维特征组成多视图数据。MSRC-v1 是一个场景识别数据集,其中有8个类,每个类有30 个样本。从中挑选了7 个类(树、汽车、人脸、奶牛、自行车、建筑和飞机)共210 张图像。从每张图像中提取多种特征组成多视图数据集Caltech7 和Caltech20,该数据集是来源于101 类的图像数据集,选择其中广泛使用的7 个类和20 个类,提取不同特征构成多视图数据集。

Table 1 Introduction of datasets表1 数据集介绍
3.2 对比方法介绍
本文将提出的OP-MVSC 与下面的方法进行对比。其中直接连接特征方法(direct)作为一种基准方法,直接将多个视图的特征拼接在一起然后执行Kmeans得到最终的结果。
Co-reg(co-regularized)[18]方法使用协同正则化方法使得不同视图的划分之间达成一致,本文仅对比其中的“成对”方法。LMSC(latent multi-view subspace clustering)[13]不是在原始特征上而是在共同的潜在表示上进行数据的重建,从而得到共同的潜在子空间表示,进而执行谱聚类得到最终结果。RMKMC(multiviewK-means clustering on big data)[19]通过获得共同聚类指示矩阵并引入ℓ2,1范数,对输入数据的异常值具有鲁棒性。mPAC(multiple partition aligned clustering)[20]方法为每个划分矩阵分配不同的旋转矩阵得到统一的聚类指示矩阵。FMR(flexible multi-view representation learning for subspace clustering)[12]方法通过希尔伯特-史密斯独立性准则(Hilbert-Schmidt independence criterion,HSIC)构造包含互补和一致信息的潜在表示,然后对潜在表示进行数据重建得到子空间表示。上述的方法,本文均按照论文中推荐的参数范围进行网格搜索并选取最好的结果。
本文使用准确率(accuracy,ACC)和F-score两个指标来衡量聚类的效果。其定义如下:定义TP(true positive)、TN(true negative)、FP(false positive)、FN(false negative)分别为判断正样本为正、判断负样本为负、判断正样本为负以及判断负样本为正。准确率定义为模型判断正确的样本占总样本的比例,表示如下:
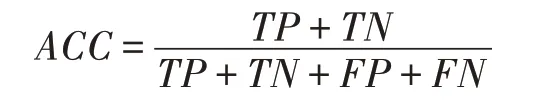
F-score是精确率(Precision)和召回率(Recall)的加权调和平均值,定义如下:

本文取β为1,即同等地看待精确率和召回率的重要性。其中精确率和召回率的定义分别为Precision=TP/(TP+FP),Recall=TP/(TP+FN)。
3.3 模型分析
本文有两个超参数{λ,γ},λ从{1 0,20,30} 中选取,γ从1.2 至1.8 的范围内以步长为0.2 进行选择。以Caltech7 为例,图1 显示了不同的超参数对聚类性能的影响。可以观察到在λ∈{1 0,20} 且γ∈{1 .6,1.8}的范围内聚类效果相当稳定,同样的结果在其他数据集上也有体现。

Fig.1 Sensitivity of parameters on Caltech7图1 数据集Caltech7 上的参数敏感性
图2 为在MSRC-v1 上随着迭代次数的增加聚类性能变化曲线,可以看出,算法在有限的迭代次数内可以达到最优的性能并保持稳定。

Fig.2 Clustering performance during iterations图2 迭代过程中的聚类性能
这也证明了从一致的表示中得到的聚类标签对后续优化中表示的学习起到了正向引导作用,进而提高了聚类性能。在不断的迭代中互相促进,从而达到更好的聚类性能。
3.4 实验结果分析
对比算法在四种真实数据集中的结果如表2 和表3 所示。其中最好的结果用粗体标注,次好结果用下划线标注。
如表2 所示,在大多数情况下,直接连接特征的方法表现出最差的性能,这表明了多视图聚类算法探索不同视图之间互补信息的有效性。本文提出的方法在不同数据集下的ACC均为最高,分别超过次好的方法2.16 个百分点、1.90 个百分点、7.26 个百分点以及0.54 个百分点。从表3 中可以看到,在F-score指标下,本文方法在Wikipedia Article、MSRC-v1 和Caltech7 上都取得了最佳的性能,分别超过次优2.00个百分点、6.48 个百分点、6.92 个百分点;仅在Caltech20 上略低于mPAC 方法。
相比于其他先进的方法,上述实验结果很好地说明了本文提出的OP-MVSC 方法的有效性。将其归因于以下两点:(1)OP-MVSC 联合优化子空间表示、划分矩阵以及聚类标签。当在某一轮迭代中产生更加准确的聚类标签时,在下一次迭代中充分利用这种高质量的标签来引导视图表示和划分的学习。通过在算法迭代中彼此促进,进而可以改进聚类性能。(2)在划分级对多视图信息进行融合,相对于相似度融合,这种划分级的融合具有更少的噪声和冗余信息,从而得到更好的聚类性能。
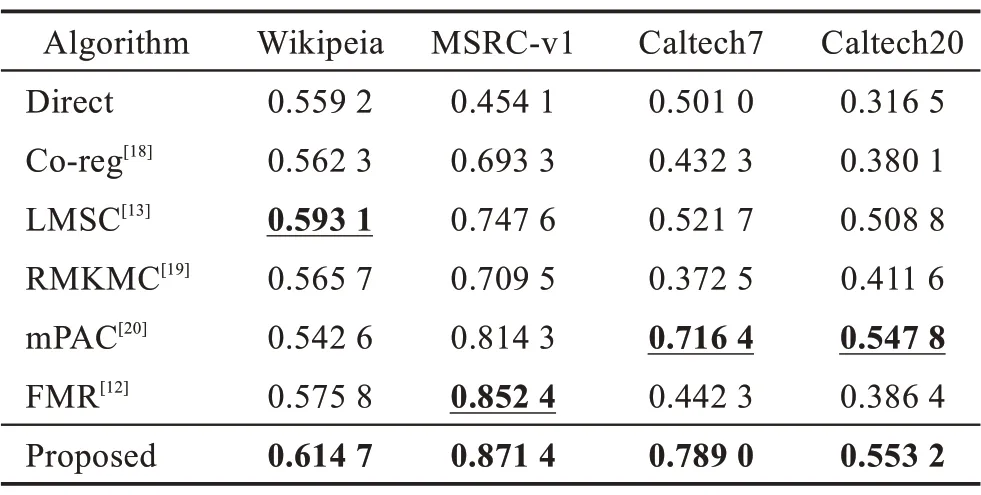
Table 2 Comparison of different algorithms under 4 datasets in terms of ACC表2 对比算法在4 个数据集下的ACC

Table 3 Comparison of different algorithms under 4 datasets in terms of F-score表3 对比算法在4 个数据集下的F-score
4 结束语
本文提出了一种新颖的单步划分融合多视图子空间聚类算法。与现有的基于相似度融合多视图信息的方法不同,本文从更富含聚类结构信息的划分级别进行融合,并引入旋转矩阵直接得到聚类结果,避免了两阶段算法分离表示学习和聚类过程的缺陷。直接将表示学习、划分融合和聚类过程统一在一个框架中,使得表示和聚类结果在迭代过程中互相促进,从而达到理想的聚类效果。多个多视图数据集上的实验结果验证了本文方法的有效性和优越性。在未来的工作中,将考虑大规模多视图聚类问题以及自适应融合的方法。
