非负半监督函数型聚类方法

姚晓红，黄恒君

兰州财经大学 统计学院，兰州 730020

聚类分析是一种数据划分的方法，其划分依据是使得同一簇内的数据具有较高的相似性，或不同簇的数据具有较低的相似性。作为一种经典的多元统计方法，几十年来，人们对聚类分析的研究持续关注；作为机器学习和人工智能的无监督学习技术，聚类分析在图像识别、商业智能和文本分析等方面得到了广泛的应用。

随着信息技术的发展和数据采集、存储能力的提高，许多学科领域均出现了一些具备连续特征的数据。例如，股票量价数据、语音数据、可穿戴智能设备监测数据、环境污染监测数据等，按照时间密集采集，本质上构成了这种数据类型。若采用泛函分析工具，将数据“连接”成曲线，并将曲线作为一个整体来进行分析，当前文献中称为函数型数据分析（functional data analysis，FDA）[1]。具体到聚类任务，则称为函数型聚类分析，是探索函数型数据的重要工具，近年来引起了学者们广泛的研究兴趣。

目前，函数型数据聚类方法主要分为两类：一类是原始数据法，该方法从离散数据出发，未考虑到数据的函数特性（如连续），本质属于高维离散数据分析方法[2-3]，本文不展开讨论；另一类是投影法，该方法以无限维函数为基础，以数据拟合为手段，通过寻找包含适当类别信息的子空间并开展聚类研究。投影法的具体算法有很多，既有从统计学视角开展的研究，如稀疏样品曲线聚类方法[4]、非参数拟合基础上的K-means 聚类算法[5-6]、基于高斯混合模型的聚类算法[7-8]等；也有从机器学习视角进行的研究，如结合自组织神经网络的函数型聚类算法[9]、基于惩罚函数的聚类一步法[10]、函数型子空间投影分割聚类算法[11]、基于模态分解的聚类算法[12]，以及局部稀疏函数型聚类方法[13]等。

事实上，上述提及的函数型数据及聚类方法仍存在一些有待进一步讨论的问题：

第一，现实当中，观测到的多数函数型数据具有取值非负的要求。例如，前面列举的各种函数型数据实例（股票量价数据等）就是这样一种情形。现有的函数型聚类方法由于未能考虑到函数型数据的这种特性，不能确保投影结果的非负性，从而可能影响聚类效果。最近，有研究将非负矩阵分解（non-negative matrix factorization，NMF）技术作为降维手段，引入到函数型数据分析中来[14]，为处理非负函数型数据提供了思路。

第二，倘若采用机器学习的术语，函数型聚类属于无监督学习任务，其优势在于无需分类标签信息即可开展数据探索研究，避免了人工密集和成本高昂的标签数据采集过程[15]。然而，正是由于忽略了标签信息，前述许多函数型聚类方法文献所报告的聚类结果精度有待进一步提高。事实上，获取少量的标签数据通常是可行的，当大量无标签数据与少量带标签数据一起学习时，能够很大程度地提高聚类精度。这种做法在机器学习领域称为半监督学习，针对非函数型数据已开展了相应的研究。与本文相关的研究有：文献[16]将概念分解应用到半监督学习中；文献[17]提出了带有局部坐标约束的半监督概念分解算法；文献[18]通过约束非负矩阵分解（constrained non-negative matrix factorization，CNMF）方法将无监督学习拓展为半监督学习；文献[19-20]将CNMF 引入聚类分析中，用以提高聚类性能。

为此，针对以上函数型数据特征及聚类方法特点，本文试图将CNMF 引入到函数型聚类分析中，讨论非负约束情况下的半监督函数型聚类方法（semisupervised non-negative functional clustering，SSNFC），旨在充分利用额外信息来提高聚类精度。

1 模型构建

本章讨论非负半监督函数型聚类模型的构建。通常，函数形式的数据不能直接观测，至多能获取具备曲线特征的离散采样点。因此，函数型数据的聚类投影法通常包含曲线拟合和聚类两个要素。本章将这两个要素合并，融入约束非负矩阵分解技术，构建了一个将曲线拟合和函数型聚类过程相统一的非负约束半监督函数型聚类模型。

1.1 曲线拟合

假定N维函数向量X(t)=[x1(t),x2(t),…,xN(t)]′为定义在连续集T 上的独立同分布函数型数据样本，xi(t)(i=1,2,…,N)是T 上的实值曲线。记yij为曲线xi(t)上带有噪音的第j(j=1,2,…,mi)个离散观测值，则yij可以由以下模型生成：

其中，tij表示yij的观测点，εij表示观测随机误差。

在实际中，式（1）中的曲线xi(t)通常假定由某个既定空间的一组基底函数线性表示：

其中，φi(t)=[φi1(t),φi2(t),…,φid(t)]′为给定的基底函数，αi=[ai1,ai2,…,aid]′为相应的系数向量。若每条曲线采用相同的基底函数拟合，且对应的离散采样点位置相同，即mi=m(i=1,2,…,N)，则结合式（2）的基底表示，式（1）可以表示为矩阵形式：

其中，Y=(yij)m×N为离散点构成的数据矩阵，E=(εij)m×N为随机误差矩阵，为基矩阵，A=[α1,α2,…,αN]d×N是待估参数构成的系数矩阵。

对于式（3），最小化目标函数

可求得系数矩阵A。其中，||·||F为矩阵的Frobenius范数，Pen为惩罚项，λ为惩罚参数。具体估计方法有回归样条（λ=0）、样条平滑（λ≠0）等[21]。

1.2 聚类过程

根据前面曲线拟合的假定，各条曲线之间的差异信息完全取决于矩阵A。因此，许多函数型聚类方法[6,13,22-23]分为两个步骤，即在曲线拟合的基础上，采用常规的聚类算法（如K-means）对系数矩阵A进行聚类。

鉴于本文处理非负函数型数据的目的，受文献[14]启示，本文首先讨论基于非负矩阵分解（NMF）的聚类过程。NMF 是一种数据降维技术，即将非负矩阵近似分解为两个低秩非负矩阵的乘积[24]：

其中，非负矩阵是指元素均大于0 的矩阵；Ud×K≥0为基矩阵；VN×K≥0 为系数矩阵。式（5）可以通过优化问题[25]进行求解。

除了降维功能外，NMF 的另一个重要性质是具有聚类特性，分解得到的低秩矩阵V能够近似体现聚类标签信息[26]。因此针对系数矩阵A的聚类，可以转化为对矩阵V进行一次常规的聚类（如K-means）[27]，即可得到原始曲线xi(t)(i=1,2,…,N)的聚类结果。将曲线拟合（式（4））与降维、聚类过程（式（5））统一在一个目标函数中，得到如下优化问题：

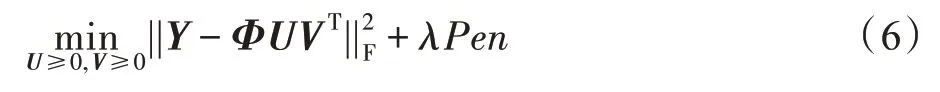
事实上，NMF 技术已经为处理具有非负特性的函数型数据提供了工具，然而在式（6）中，并未考虑到数据的标签信息，本质上属于无监督学习。而实际上，在数据采集过程中，获取少量数据的标签信息是可行的，当大量无标签数据与少量带标签数据一起学习时，能够很大程度地提高聚类精度。

1.3 非负约束半监督函数型聚类模型

为充分利用数据的标签信息，本文引入CNMF[18]技术，将数据的标签信息融入函数型聚类过程中，从而将无监督学习扩展为半监督学习。为此，首先构造数据的标签矩阵：

其中，N为样本量；l为带标签信息的样本点个数；Cl×c是指标矩阵，当样本点xi（i=1,2,…,l）属于类Cj（j=1,2,…,c，c≤K）时，cij=1，否则cij=0；O是零矩阵；IN-l是N-l阶单位矩阵。例如，当l=5 时，表示样本中带有标签信息的样本点有5 个，分别记为x1、x2、x3、x4、x5，剩余N-5 个样本点没有标签信息。若x1属于第一类，x2、x3属于第二类，x4、x5属于第三类，则相应的标签矩阵为：

为了将数据的标签信息融入聚类分析中，引入辅助矩阵Z，使：

显然，由非负约束条件V≥0 可知，辅助矩阵Z也是非负的，即Z≥0。

将式（7）代入式（5），可得：

即实现了CNMF。式（8）给出了函数型数据的低维表示，具体地，乘积矩阵LZ的行向量对应于样本点的低维表示。同时，CNMF 能够保证具有相同标签的样本点在低维空间中也属于同一类。显然，式（8）将标准的NMF 扩展为半监督学习。相应地，式（6）的优化问题可进一步表述为：

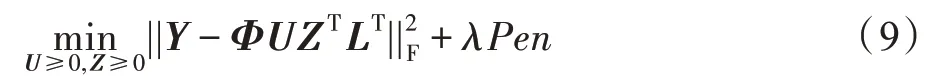
最后，鉴于稀疏性表示有助于提高聚类性能[28]，而l2,1范数正则化是实现稀疏特征选择的有效方法之一。因此，取式（9）中的惩罚项Pen=||LZ||2,1，由于标签矩阵L是常量矩阵，惩罚项可进一步简化为||Z||2,1。

综上所述，将曲线拟合和聚类过程统一在一个目标函数中，即得到本文提出的非负约束半监督函数型聚类模型（SSNFC）：

2 求解算法

本章首先给出模型的求解过程及算法，接着证明算法的收敛性，并进行时间复杂度分析。

2.1 求解过程

由于目标函数（式（10））对于参数U、Z来讲并非是一个联合凸优化问题，很难求到全局最优解。但对于U（Z固定）或Z（U固定）来讲，均是凸优化问题。因此，本文依据非负矩阵分解的乘性迭代更新算法[25]，提出了模型的参数求解算法。具体地，固定其中一个变量Z（U），通过式（10）求解另一个变量U（Z）。

令Θ、Γ分别为非负约束条件U≥0 和Z≥0 的拉格朗日乘子，则相应的拉格朗日函数为：

得到U、Z更新规则分别为：

根据式（11）和式（12）可交替迭代更新参数U、Z，实现优化问题（目标函数式（10））的求解，即实现非负半监督函数型聚类算法（SSNFC）。

算法1非负半监督函数型聚类算法（SSNFC）

输入：数据矩阵Y、基矩阵Φ、惩罚参数λ和类别数K。

1.构造数据的标签矩阵L

2.初始化U0、Z0

3.fort=1,2,…,最大更新迭代次数

4.固定Zt-1，根据式（11）更新Ut-1

5.固定Ut，根据式（12）更新Zt-1

6.if 式（10）收敛

7. break

8.end if

9.end for

输出：U、Z和簇划分C={c1,c2,…,cK}。

在该算法中，需要说明：

（1）对于矩阵U、Z的初始化，可采用0～1 之间的均匀随机数填充。

（2）对于迭代的终止条件，包括两方面：一是式（10）收敛，即同时满足条件||Ut-Ut-1||∞≤ε0，||Zt-Zt-1||∞≤ε0和，其中ε0和ε1为很小的正数；二是达到预先设定的最大迭代次数。

2.2 算法收敛性

显然，目标函数（式（10））的下界大于等于0，因此，只需证明目标函数（式（10））在更新规则（式（11）和式（12））下是非增的，即：

定理目标函数OF在更新规则（式（11）和式（12））下是非增的，当且仅当U、Z是稳定点时目标函数值在更新规则下保持不变。

定理保证了算法的收敛性，从而得到局部最优解。为了证明定理，首先介绍辅助函数的定义和引理[25]，然后构造辅助函数，并证明定理，即证明算法的收敛性。

定义若G(x,xt)满足条件

G(x,xt)≥F(x)，G(x,x)=F(x)

则称G(x,xt)是F(x)的辅助函数。

引理若G(x,xt)是F(x)的辅助函数，则F(x)在更新规则

下是非增的。

证明由辅助函数的定义知，需要证明F(xt+1)≤G(xt+1,xt)≤G(xt,xt)≤F(xt)。显然，当xt是G(x,xt)的局部极小值时，有F(xt+1)=F(xt)。若F(x)可导，且在xt的小邻域内连续，即∇F(xt)=0，则通过式（13）的迭代更新，可得到收敛于F(x)局部极小值xmin=arg minxF(x)的序列：

即引理得证。

由引理可知，通过寻找恰当的辅助函数，能够证明目标函数（式（10））在更新规则（式（11）和式（12））下是非增的。因此，下面首先构造辅助函数，然后证明定理。

命题1令F′是函数F的一阶导函数，则

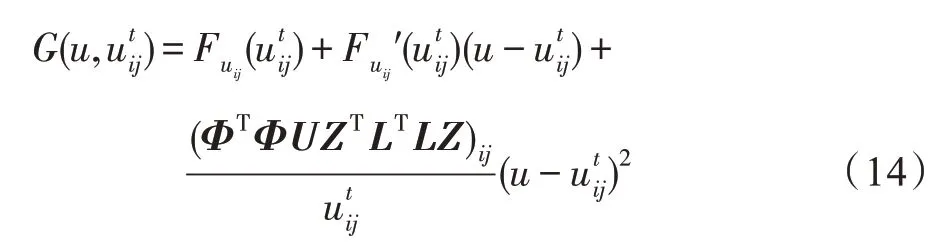
是函数Fuij(u)的辅助函数，其中Fuij(u)是目标函数OF中关于uij的部分。

式（14）和式（15）分别是构造的辅助函数，由此可进一步证明定理，证明过程如下：

2.3 时间复杂度分析

本文进一步讨论SSNFC 的计算复杂度。按照本文使用的符号，N是总样本量，m是特征数量，d是基底个数，l是带标签数据的样本点个数，c是带标签数据的类别数，K是聚类数。注意，SSNFC 实际包括两个过程：一是投影，即曲线拟合Y=ΦA，因迭代更新前只计算一次，所以其计算复杂度可忽略不计；二是CNMF。

显然，在该算法中，标签矩阵L是一个常量矩阵，每一行只有一个元素为1，其余元素均为0，因此矩阵乘积LZ的计算复杂度为O((c+N-l)K)，且每次迭代过程中只计算一次。计算复杂度主要在于U和Z的更新迭代过程中，具体如下：

在U的更新过程中，每次更新进行了(c+N-l)K+dmN+3dNK+d2K+d2m次加法运算，(c+N-l)K+dmN+3dNK+d2K+d2m+dK次乘积运算，dK次除法运算，共进行了2(c+N-l)K+2dmN+6dNK+2d2K+2d2m+2dK次运算。

在Z的更新过程中，每次更新进行了(c+Nl)Nm+3(c+N-l)md+(c+N-l)K+3(c+N-l)dK+NK次加法运算，NK+(c+N-l)Nm+3(c+N-l)md+3(c+Nl)K+3(c+N-l)dK次乘积运算，2(c+N-l)K次除法运算，共进行了2(c+N-l)Nm+2NK+6(c+N-l)md+6(c+N-l)K+6(c+N-l)dK次运算。

综上所述，若不计投影过程，每次迭代过程的计算复杂度为O(mNK)，记t为迭代次数，则进行t次迭代更新的计算复杂度为O(tmNK)。

3 模拟及实例验证

为了说明本文提出的SSNFC 方法的有效性，下面采用随机模拟数据和实例数据，将SSNFC 与无监督函数型聚类方法（TA 方法[22]、FCOF 方法[10]和FNMF（functional nonnegative matrix factorization）方 法[14]）进行比较，以聚类纯度（Purity）、聚类精度（Accuracy）和兰德指数（Rand index，RI）为聚类效果的评价准则。其中，TA 是函数型聚类两步法，FCOF 是函数型聚类一步法，FNMF 是基于非负矩阵分解的函数型聚类方法。数据模拟及算法比较通过R语言实现。实验的计算机环境为：Intel®CoreTMi7-8700K CPU 3.7 GHz，内存16 GB，Windows10 64 位操作系统。

3.1 数据

3.1.1 模拟数据

参照文献[7]，本文采用三角函数和多项式函数的线性组合随机模拟生成一个数据集。具体生成公式如下：

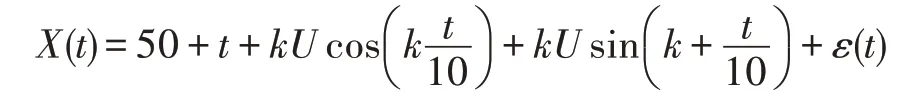
其中，U是服从正态分布N(1,1) 的随机变量；ε(t)～N(0,1)是白噪声；k分别取1、3 和5，表示生成3 类数据；t∈[1,21]，共取1 001个等距的离散点，即t=1,1.02,1.04,…,21。每类随机生成50 条曲线，如图1 所示。

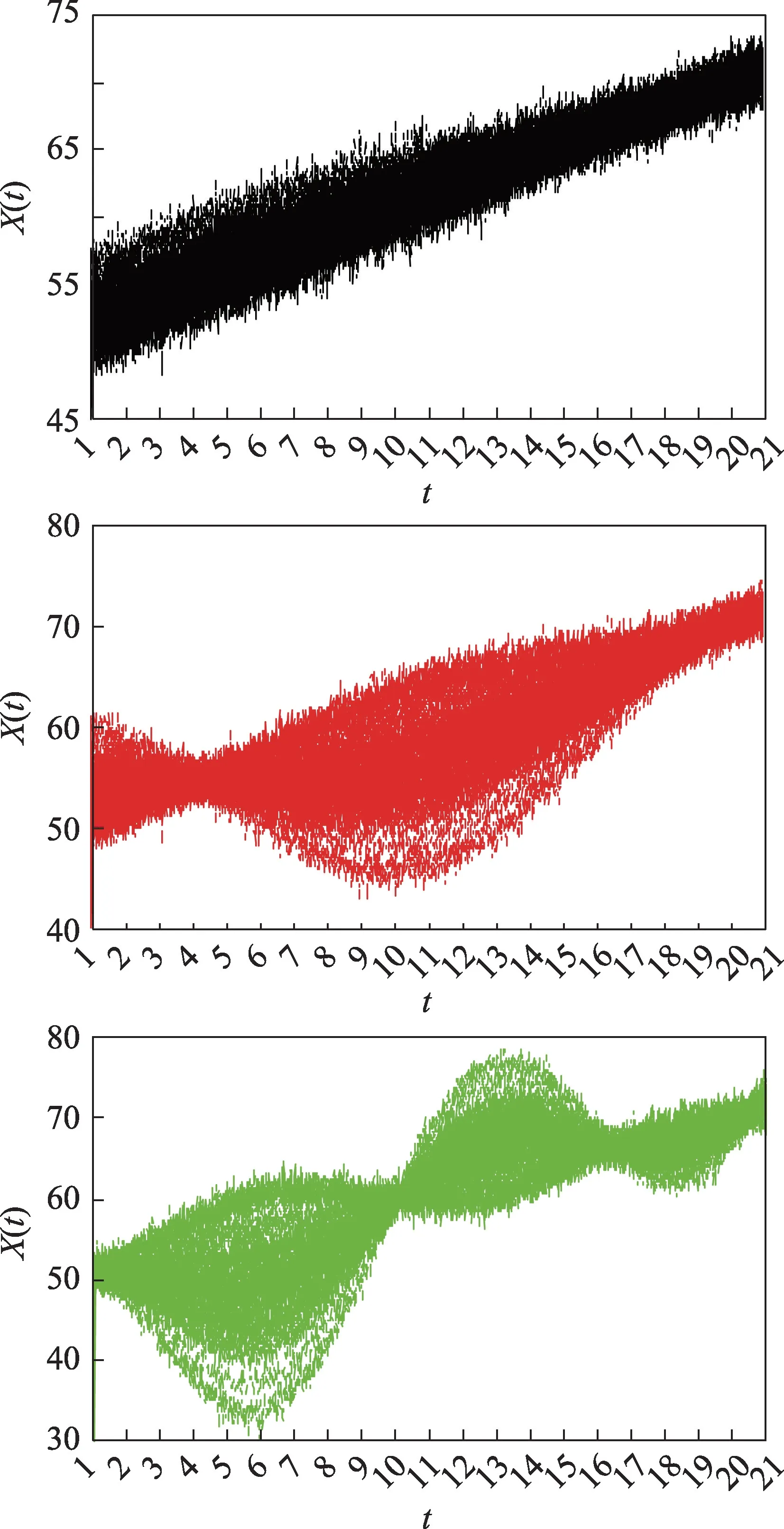
Fig.1 Simulation data图1 随机模拟数据

3.1.2 Growth 数据

Growth 数据集（来自R 扩展包fda）包含54 名女孩和39 名男孩1～18 岁之间31 个阶段的身高数据。样本及类别标签如图2 所示，其中横坐标表示年龄，纵坐标表示身高，不同颜色和线型代表不同性别。

3.1.3 TIMIT 语音数据

选取TIMIT（Texas Instruments and Massachusetts Institute of Technology）语音数据库（http://web.mir.edu/course/6/6.863/share/nltk_lite/）中名为“SA1”的语音数据。该库是由麻省理工学院、斯坦福研究所和德州仪器共同设计完成的，收集了美国不同方言读出给定句子时的语音数据，被广泛应用于语音识别研究领域。本文选用其中经过数字信号处理后的音素数据和对应的音素类别标签。具体地，“SA1”语音中包含“sh”“dcl”“iy”“aa”和“ao”五个音素，其中“sh”表示“she”，“dcl”表示“dark”，“iy”表示“she”中的元音，“aa”表示“dark”中的元音，“ao”表示“water”中的第一个元音。原始数据的一个样本示例及类别标签如图3所示，其中横坐标表示频率，纵坐标表示经对数周期图法处理的音频数据值，不同线型代表音素类别。

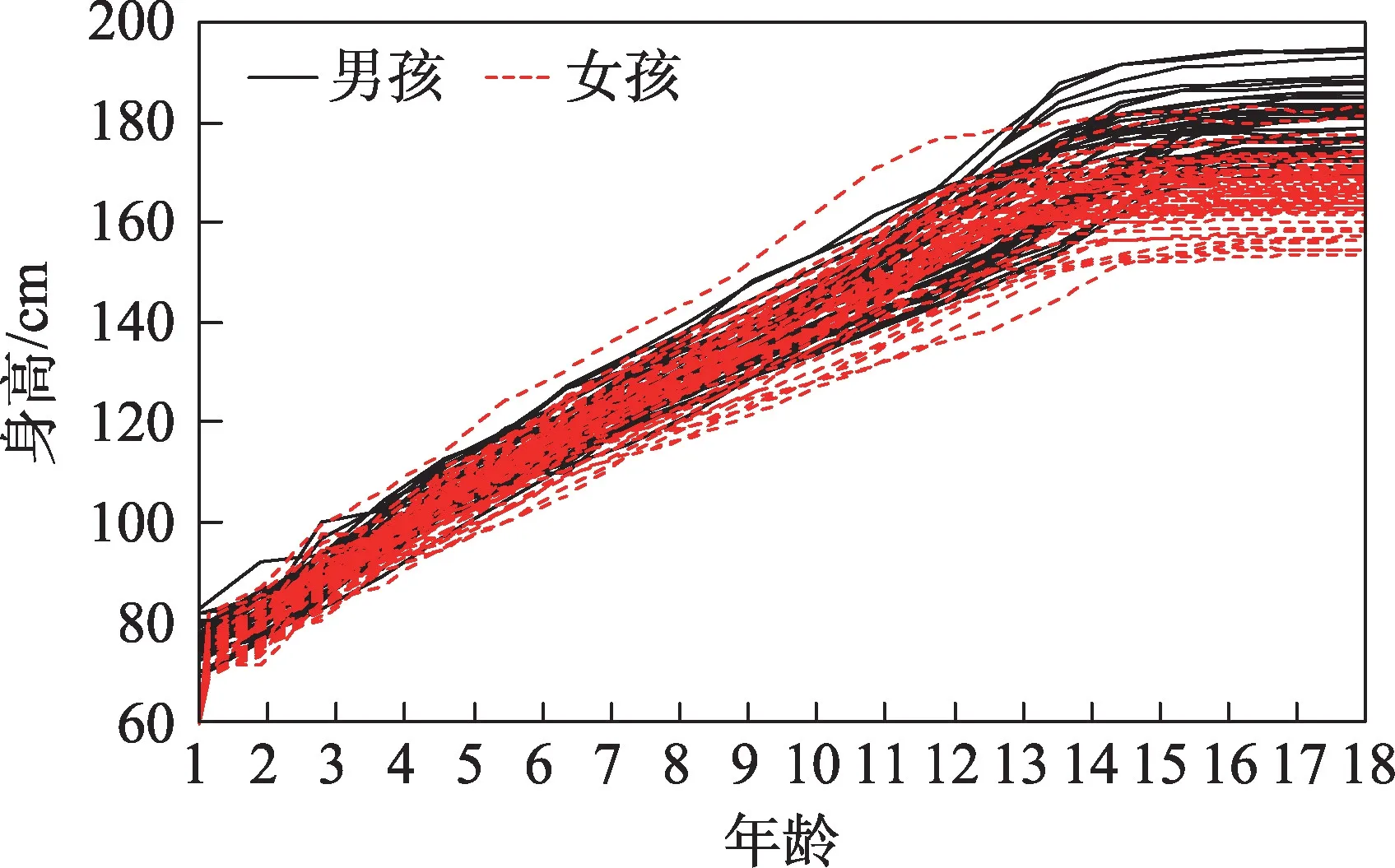
Fig.2 Growth data图2 Growth 数据

Fig.3 TIMIT speech data图3 TIMIT 语音数据

3.2 评价准则

本文采用聚类纯度（Purity）、聚类精度（Accuracy）和兰德指数（RI）来评价聚类效果，定义如下：

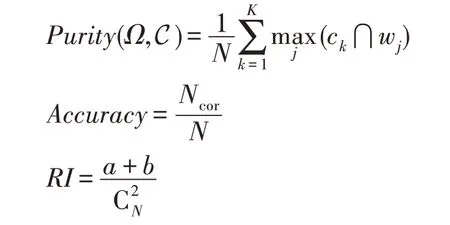
其中，N为样本量，K为类别数；Purity(Ω,C)表示聚类纯度，Ω={w1,w2,…,wK} 表示真实类别，wj(j=1,2,…,K)为第j类，C={c1,c2,…,cK}表示实际聚类结果，ck(k=1,2,…,K)为第k个聚类簇；Accuracy表示聚类精度；Ncor为正确聚类的样本点个数；RI表示兰德指数；a表示在真实类别与实际聚类结果中都属于同一类的元素对数；b表示在真实类别与实际聚类结果中都不属于同一类的元素对数；为数据集中两两可以组成的对数。上述三种聚类评价指标取值均介于0 到1 之间，值越大，则聚类效果越好。

3.3 参数设置

在进行聚类时，SSNFC算法参数设定如下：（1）采用三次等距节点B-样条基底拟合曲线，通过基底数量控制曲线平滑程度，3 组数据的基底数量分别设置为20、20、23；（2）随机模拟数据包含3 类数据，取聚类数K=3，Growth 数据中性别包含男、女，取聚类数K=2，TIMIT 语音数据中包含5 种不同的音素，取聚类数K=5；（3）数据的标签矩阵L依据样本所含标签信息的多少确定；（4）惩罚参数λ依据聚类效果确定，聚类评价指标值越大，说明聚类效果越好。

在参数设定基本一致的基础上，利用随机模拟数据、Growth 数据和TIMIT 语音数据，将SSNFC 方法和TA 方法、FCOF 方法和FNMF 方法的聚类性能进行比较。

3.4 评价结果

为了消除初始化对聚类结果的影响，每个实验重复进行100 次，用评价指标的均值来衡量聚类性能。

首先，分别取λ={0.01,0.10,1.00,10.00,100.00}，在随机模拟数据、Growth 数据（随机抽样，样本量为90，其中女孩51 人，男孩39 人）和TIMIT 语音数据中均加入10%的标签信息进行聚类，采用聚类纯度（黑色实线）、聚类精度（红色虚线）和兰德指数（蓝色虚线）来评价聚类效果，结果如图4 所示。

由图4可以看出，针对随机模拟数据（上）、Growth数据（中）和TIMIT 语音数据（下），超参数λ的取值对聚类效果的影响有所差异，但整体来看，超参数λ取值较小时，不利于提高聚类性能，尤其在随机模拟数据和Growth 数据上表现得比较明显。超参数λ的取值大小体现了稀疏性惩罚项的正则化程度，取值越大，说明稀疏性正则化更有助于提高聚类性能。

然后，分别取λ={0.01,0.10,1.00,10.00,100.00}，在随机模拟数据、Growth 数据和TIMIT 语音数据中依次加入10%、20%、30%、40%、50%的标签信息进行聚类，结果如图5 所示。

Fig.4 Variation tendency of clustering effect with hyper-parameter λ图4 聚类效果随超参数λ 的变化趋势

图5 中，Proportion 表示数据中所含标签信息的比例，分别取10%、20%、30%、40%和50%。可以看出，无论是随机模拟数据（上）、Growth 数据（中），还是TIMIT 语音数据（下），SSNFC 方法的聚类效果与超参数λ的取值和样本所含标签信息的多少均有关。不管超参数λ取何值，样本所含标签信息越多，聚类效果则越好。而对于超参数λ，与前面的分析有一致的结论。

最后，将半监督函数型聚类方法SSNFC 与无监督函数型聚类方法（TA 方法、FCOF 方法和FNMF 方法）的聚类效果进行比较，其中SSNFC 方法聚类时，数据中加入了20%的标签信息。

随机模拟数据的聚类评价结果如表1 所示。Growth 数据的聚类评价结果如表2 所示。TIMIT 语音数据的聚类评价结果如表3 所示。

Fig.5 Variation tendency of clustering effect with hyper-parameter λ and label information图5 聚类效果随超参数λ 和标签信息的变化趋势

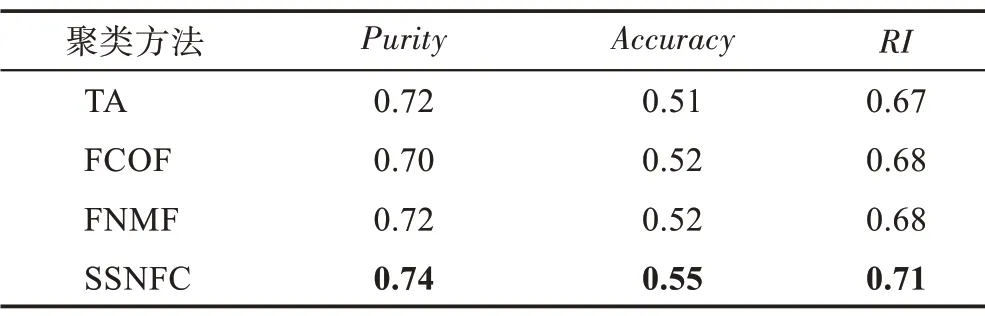
Table 1 Clustering evaluation results of simulation data表1 随机模拟数据聚类评价结果

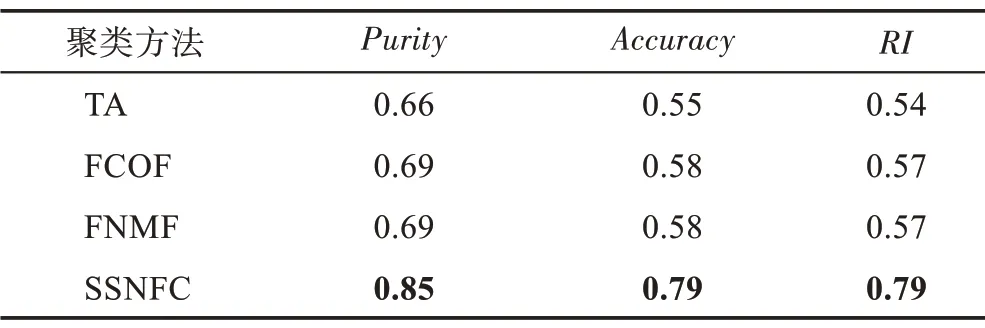
Table 2 Clustering evaluation results of Growth data表2 Growth 数据聚类评价结果

显然，对于随机模拟数据、Growth 数据和TIMIT语音数据，不管是聚类纯度、聚类精度，还是兰德指数，半监督函数型聚类方法SSNFC 均优于其他无监督函数型聚类方法，尤其是SSNFC 在Growth 数据上的表现，明显优于其他方法。

4 结束语

本文在半监督学习框架下，讨论了非负函数型数据的聚类问题。在考虑函数型数据拟合和聚类的同时，也考虑了数据的标签信息。具体地，通过引入CNMF，将数据的标签信息融入到函数型聚类过程中，然后将数据拟合、非负约束及聚类过程纳入同一个目标函数，构建了一个新的非负约束半监督函数型聚类模型，并给出模型的求解算法，同时也讨论了算法的收敛性和计算复杂度。模拟和实例验证结果显示，该方法有助于提高聚类性能。

然而，在实际中，函数型数据通常会以多元的形式出现，例如个人穿戴式智能设备至少监测心率、血压和运动轨迹，气象数据一般包括温度、湿度和风力等指标，空气质量监测数据涉及到二氧化氮、二氧化硫、一氧化碳、臭氧和细微颗粒物等指标。若仍采用一元函数型数据的处理方式选取单项指标进行数据分析，显然不能达到认识事物全貌的目的。因此，在半监督学习框架下，进一步讨论针对多元函数型数据的聚类方法，具有十分重要的理论价值和实际意义。另外，对于多元函数型聚类方法，由于各变量对聚类结果的贡献不尽相同，如何确定权重系数也是进一步关注的问题。