不平衡供电条件下多脉动整流器的谐波特性分析

李亚辉，孙媛媛，李可军，许庆燊，王庆岩

（电网智能化调度与控制教育部重点实验室（山东大学）,山东省济南市 250061）

0 引言

随着电力电子技术的飞速发展,非线性电力电子装置广泛接入电网。基于晶闸管的相控整流装置具有结构简单、直流电压波动小等优点［1-3］,在高压直流输电、直流电机供电、通信设备电源、电动汽车、电解、冶金等领域获得广泛应用［4］。以三相6 脉波整流电路为基础的多脉波整流器,如12 脉波整流器［4-6］、24 脉波整流器［7-9］甚至更高脉波次数的整流器,通过将多组三相整流电路直流侧串联或并联,实现直流侧单个周期内更高的脉波次数［10-12］。多脉波整流器兼具三相6 脉波整流器的优势,同时交流侧电能质量更好、功率密度更高［13-14］,广泛应用于高压直流输电、变频调速、飞机电源系统等场合［15-16］。由于线路、负荷等原因,整流装置交流侧供电电压存在不平衡现象,各相谐波电压呈现差异化特征,导致整流器的谐波发射特性随之改变［4-5］。整流装置的非线性特征给电网造成谐波污染,而不平衡电压会使得整流装置产生非特征谐波。对功率较大的整流装置,非特征谐波的影响不容忽视。

在频域中建立谐波耦合模型（harmonic coupling model,HCM）分析谐波源的谐波产生特性,相比于时域模型,可更清楚地揭示谐波源的谐波产生机理,同时可将谐波电压与谐波电流之间的时域非线性特征转化为频域线性关系［17-18］,可更好地应用于系统谐波潮流计算、谐波责任划分等［19］。三相桥式整流电路在理想电压工况下的频域谐波模型［20-22］开辟了谐波源谐波耦合建模的新思路,但所提出的模型未考虑电压不平衡工况,尚未分析非特征谐波的产生。文献［23-24］基于实测数据建立了居民负荷HCM,但基于实测数据的模型难以明确谐波产生及耦合原因。文献［25］分析了模块化多电平换流站中扰动分量与稳态谐波的耦合交互作用,文献［26］基于不同种类谐波源参数特点,建立考虑电压波动的谐波源频域模型,所建模型均较难应用于多脉波整流器的稳态分析中。文献［4-5］针对电压不平衡下12 脉波整流器HCM 进行了求解,通过对正序和负序电压分别建模,得到非理想电网供电情况下的谐波模型。现有文献在进行精确建模时,主要针对单一类型的整流电路进行谐波分析［4-5,17-22］,模型尚不具有通用性。

为提升HCM 通用程度,明晰非理想供电情况下整流电路的谐波耦合特性,尤其是不平衡电压对非特征谐波造成的影响,揭示各次谐波电压和谐波电流之间的耦合关系,本文研究了考虑供电电压不平衡的三相6 脉波整流器频域HCM,并将其扩展应用至多脉波整流器。为适应各类供电情况,将三相电压分解为电压平衡分量及不平衡分量,分析交直流谐波电压特征,给出不平衡分量导致的直流电压谐波与电压波动的关系,建立交流侧谐波电压与电流的耦合关系,研究了由电压不平衡导致的非特征谐波电流,通过附加谐波耦合导纳矩阵,明确了电网电压不平衡电压分量对交流电流的影响。同时,为适应各类型多脉波整流方式,考虑各整流桥输入电压与相电流的耦合关系,以12 脉波整流器为例建立谐波耦合导纳矩阵模型,将所提模型扩展至多脉波整流装置中。

1 不平衡供电条件下的整流电路电压

1.1 交流侧供电电压

三相6 脉波整流电路谐波分析时的等效电路如图1 所示［2-3］,其中：um为三相供电电压,m=A,B,C；im为三相电流；Ls为换相电抗；udc和idc分别为直流侧电压和电流；R和L分别为直流侧负载等效电阻和电抗；Edc为直流电动势。

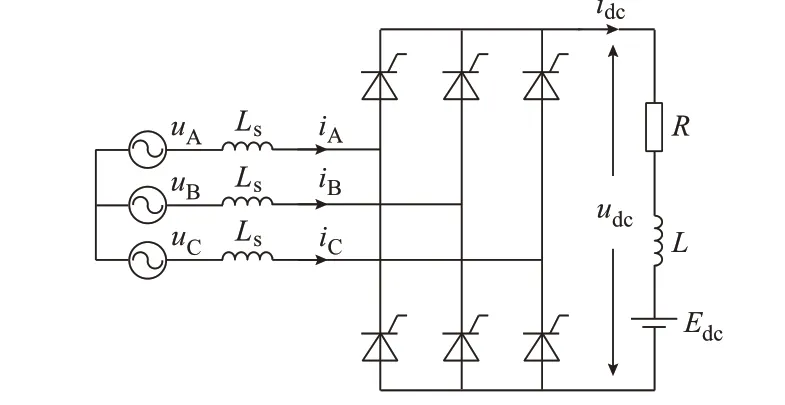
图1 三相6 脉波整流电路Fig.1 Three-phase six-pulse rectifier circuit

实际电网电压存在不平衡,交流侧端口电压u′m(t)可写成如下形式：

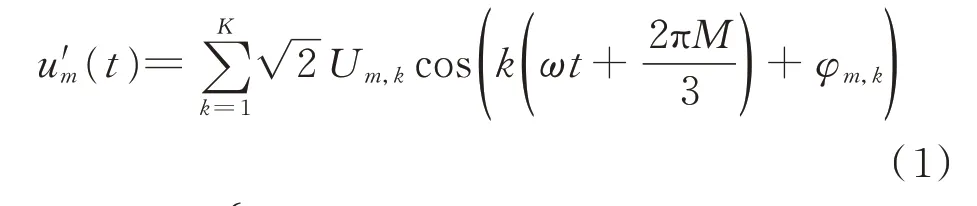
式中：M为区分相位的系数（A 相M=0,B 相M=−1,C 相M=1）；Um,k为m相第k次谐波电压幅值；φm,k为m相第k次谐波电压相角；K为所考虑的最高次谐波电压次数；ω为电网基波电压角频率。

当考虑三相电压不平衡及谐波差异时,以UA,k和φA,k为参考,可将m相电压写为如下形式：

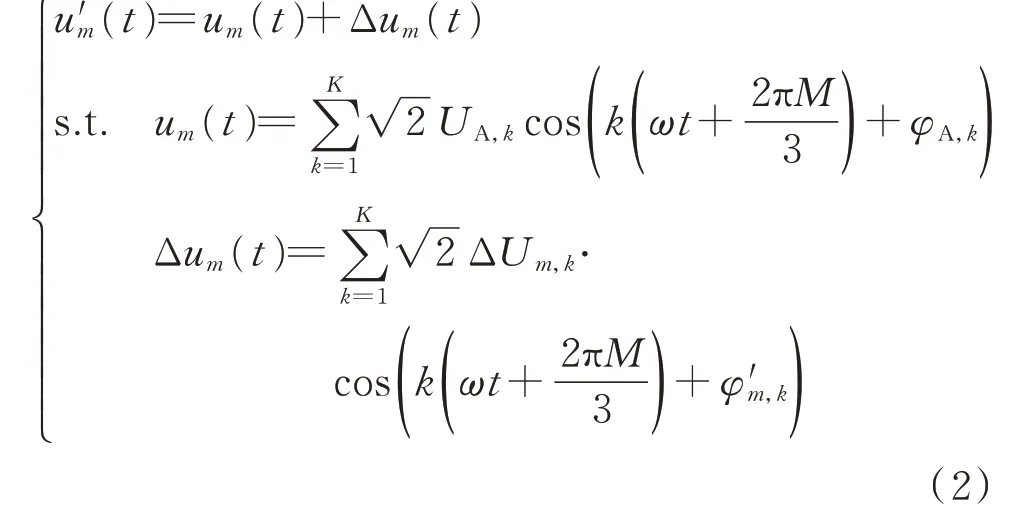
式中：um(t)和Δum(t)分别为m相电压的平衡分量和不平衡分量；ΔUm,k为m相与A 相的第k次谐波电压幅值的差值；φ′m,k为m相不平衡分量中第k次谐波电压的相角。

1.2 直流侧电压

三相6 脉波整流电路交流侧和直流侧的电压之间的调制关系,可利用考虑换相过程的梯形电压开关函数进行描述［4］,得到不平衡工况下直流电压u′dc(t)与平衡分量产生的直流电压udc(t),其差值Δudc(t)为B 相及C 相不平衡分量产生的直流电压。经推导,可将m相不平衡电压分量造成的直流电压差表示为式（3）。

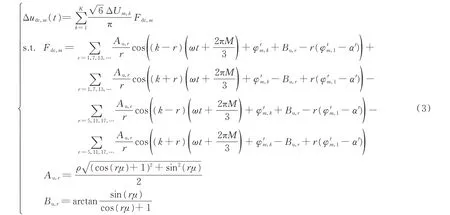
式中：Au,r和Bu,r为考虑晶闸管换相过程后电压开关函数的校正系数；r为电压开关函数中的谐波次数；μ为晶闸管换相角。供电电压不平衡时,晶闸管触发和关断时刻均发生偏移,利用系数ρ和α′分别对供电电压不平衡时导通时间及触发角进行修正。由式（3）可知,在非理想电压情况下,直流侧电压不仅包含理想工况下的6k次特征谐波,而且包含6k±2 次非特征谐波。

各相的不平衡电压分量都会对每个周期中1/3的脉波数造成影响。当不平衡分量占比较大时,直流电压的差值随之增大,同时造成直流侧电压波动的增强。由式（3）可得m相不平衡电压分量对直流侧电压波动的影响,电压波动量ΔUdc为：

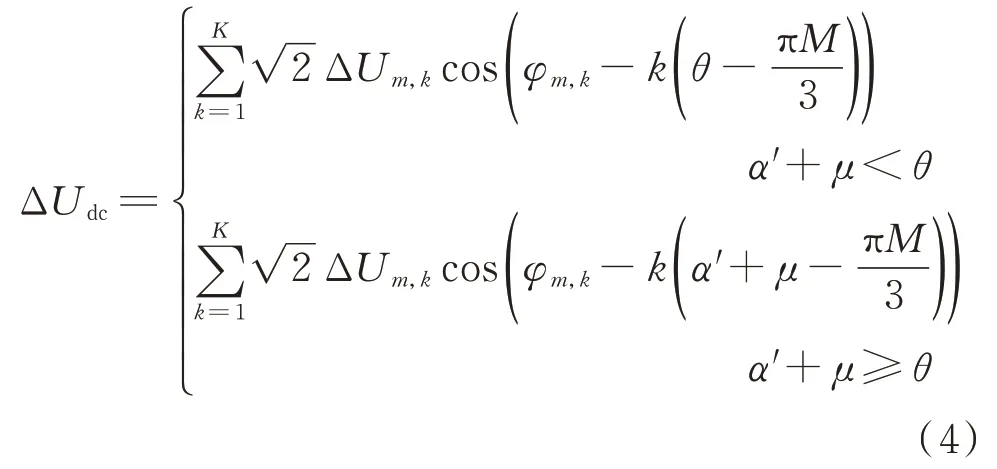
式中：θ为Δudc(t)取得直流电压最大值时对应的角度,理想工况下θ为π/6。当考虑电压不平衡及谐波差异时,θ存在小角度的偏移。直流侧k次谐波电压对应的阻抗为Zk=R2+(kωL)2,阻抗角为βk=arctan(kωL R)。由于直流侧负载特性仅影响各次谐波电流的相位但不影响谐波频次,因而直流电流的谐波电流特征与直流电压相同。

2 不平衡供电条件下谐波电流特性分析

由于不平衡电压的存在,直流电流中的6k±2 次非特征谐波分量既会导致6k±1 次特征谐波的变化,又会产生6k±3 次非特征谐波［4-5］。采用梯形函数修正电流开关函数,校正系数Ai,s和Bi,s为：

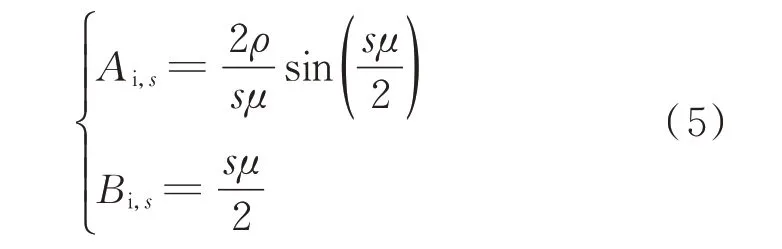
式中：s为电流开关函数中的谐波次数。

由此可建立供电不平衡时的HCM,明确不平衡电压与6k±1 次特征谐波电流以及6k±3 次非特征谐波电流之间的关系,分析不平衡电压的影响。供电不平衡时谐波电流矩阵I′A为：

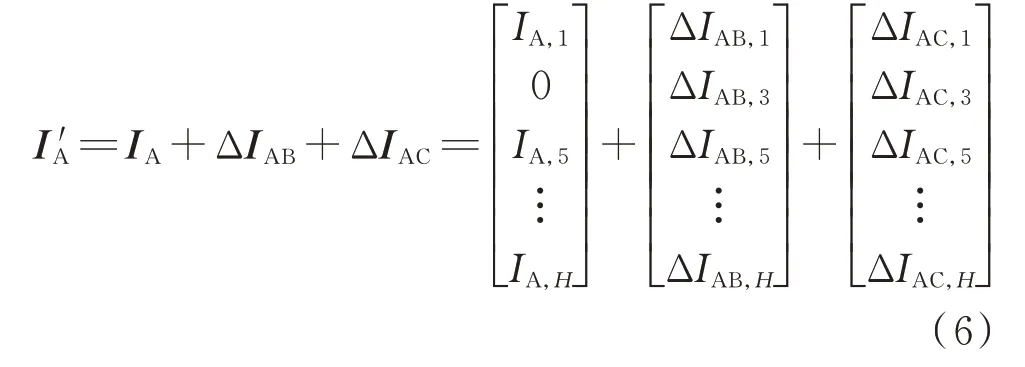
式中：IA为仅考虑平衡电压um(t)时由特征谐波电流IA,h构成的矩阵［20-23］；ΔIAB和ΔIAC分别为由B 相和C 相不平衡电压所产生的h次谐波电流ΔIAB,h和ΔIAC,h构成的矩阵,用于明确不平衡电压分量对交流电流特征及非特征谐波的影响；H为最高谐波次数。

以ΔIAB为例,矩阵中ΔIAB,h表示B 相不平衡电压分量ΔUB,k对A 相第h次谐波电流的影响,构成的附加耦合导纳矩阵为：

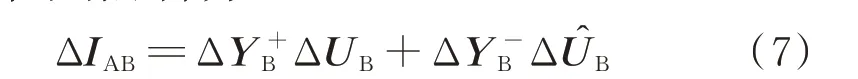
式 中：ΔUB和ΔÛB分 别 为 由B 相 不 平 衡 电 压 分 量ΔUB,k∠φ′B,k和ΔUB,k∠(−φ′B,k)构成的矩阵；ΔY+B和ΔY−B分别为ΔUB和ΔÛB对应的附加耦合导纳矩阵。类似的,可建立C 相不平衡电压分量对应的附加谐波耦合导纳矩阵。附加耦合导纳矩阵ΔY+m和ΔY−m中各元素的具体形式见附录A 式（A1）—式（A4）。

基于上述分析,考虑电压不平衡的三相6 脉波整流电路的HCM 为：

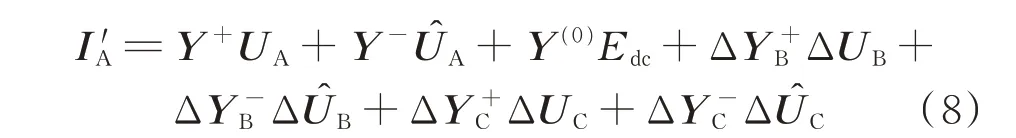
式中：UA和ÛA分别为由A 相电 压 分量UA,k∠φA,k和UA,k∠(−φA,k)构成的矩阵；Y+和Y−分别为UA和ÛA对应的耦合导纳矩阵；Y(0)为直流电动势Edc对应的耦合导纳矩阵；ΔUC和ΔÛC分别为由C 相不平衡电压分量ΔUC,k∠φ′C,k和ΔUC,k∠(−φ′C,k)构成的矩阵。

所提模型分别考虑谐波电流与平衡电压分量、B 相和C 相不平衡电压分量耦合关系,明确了不平衡电压造成的影响。附加耦合导纳矩阵可直观地体现出不平衡电压所产生的非特征谐波的次数和含量,同时也可反映出不平衡电压对特征谐波的影响。另外,频域下的HCM 无须重复求解谐波耦合导纳矩阵,可适应供电电压的动态变化。

在整流器实际运行过程中,由于晶闸管存在通态压降,其杂散因素将导致电流毛刺及电压过冲现象。在HCM 建立过程中,忽略了晶闸管参数差异对建模造成的影响,一方面,相比于整流电路运行电压,晶闸管通态压降几乎可以忽略,另一方面,杂散因素仅在晶闸管换相瞬间对输入电压、电流造成影响,不影响整流电路稳态特性。

3 不平衡供电时多脉波整流器的谐波分析

串联型多脉波整流方式在兼顾三相6 脉波整流电路优势的同时,其交流侧电能质量更好,在大功率场合获得广泛应用［13-14］。面对多脉波整流器应用需求,所提模型可拓展应用至任意脉波整流器的谐波分析中,以最为常见的12 脉波整流器为例进行扩展。

在12 脉波整流器正常运行情况下,采用星形/星形/三角形三绕组变压器产生2 组幅值相同、相位相差δ=π/6 的三相交流电压,每个周期均可在直流侧产生12 脉波［4-6］,其等效电路如图2 所示,其中1∶KT表示原边绕组与第1 个整流桥所连副边绕组的匝数比。

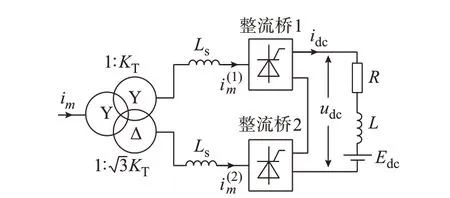
图2 串联型12 脉波整流电路Fig.2 12-pulse series-connected rectifier circuit

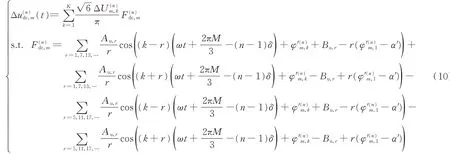
利用直流侧电压、电流关系及电流开关函数,可建立12 脉波整流器HCM。分别考虑整流桥输入电压中平衡电压、不平衡电压分量作用,以第n个整流桥A 相电流为例,其模型如式（11）所示,模型中矩阵各元素的具体表达式详见附录A 式（A1）—式（A7）。

理想运行工况下,12 脉波整流器的电网侧仅包含12k±1 次特征谐波电流［4］,但在不平衡供电条件下不能有效抑制6k±3 次谐波电流,且由于上、下整流桥的输入电压差异,5 次、7 次等非特征谐波电流也将流入电网。基于所提模型,不仅可明确12 脉波整流器中特征谐波和非特征谐波含量,还可用于确定各整流桥各相平衡电压分量和不平衡电压分量对各次谐波电流的贡献。

值得注意的是,本章以最为常见的12 脉波整流器为例,在面对更高脉波次数的整流装置时,可增加其余整流桥输入电压与相电流之间的耦合关系,并结合移相变压器结构,建立HCM,进一步扩展所提谐波耦合模型的应用范围。

4 算例分析

4.1 仿真分析

在MATLAB/Simulink 中搭建三相6 脉波及12 脉波整流电路的仿真模型,设置不同运行工况,验证HCM 的准确性。

4.1.1 参数设置

电网输入的基波电压有效值为220 V,频率为50 Hz,基波电压初始相角φ1为60°,换相电抗Ls为2 mH,考虑的最高谐波次数为31 次。表1 设置4 个算例Case 1 至Case 4 对三相6 脉波整流电路模型进行验证；设置Case 5 和Case 6 对12 脉波整流电路模型进行验证,输入电压参数分别同Case 1 和Case 3,未做修正的触发角α和晶闸管换相角μ依据高压直流输电系统运行参数分别取10°和20°左右,变压器变比KT取1。表1 中,ε表示三相电压不平衡度,其定义如下：

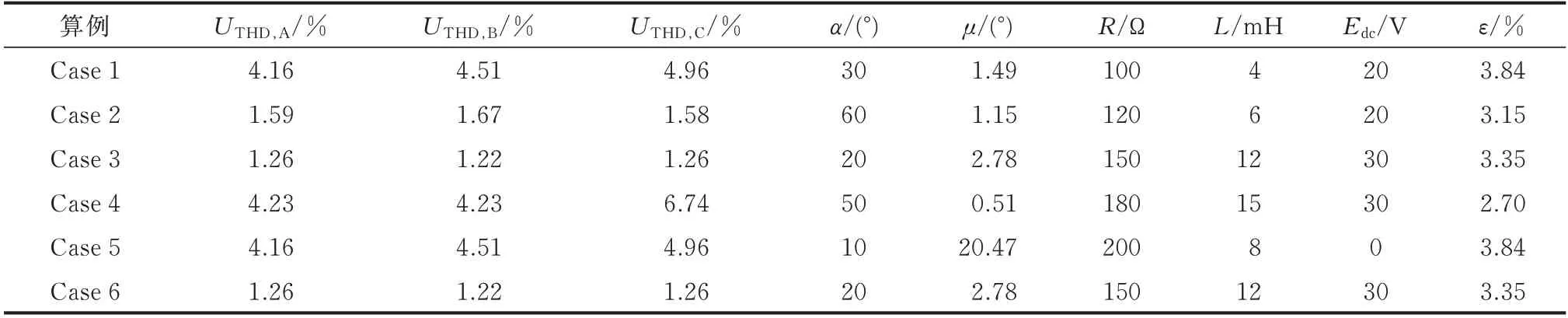
表1 整流电路运行参数Table 1 Parameters of rectifier circuit

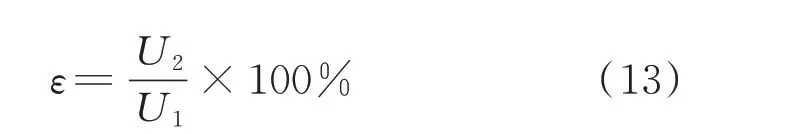
式中：U1和U2分别为三相电压的正序和负序分量。

采用总谐波畸变率（total harmonic distortion,THD）评估谐波含量,UTHD,m和ITHD,m分别表示m相电压和电流THD,表达式如下：

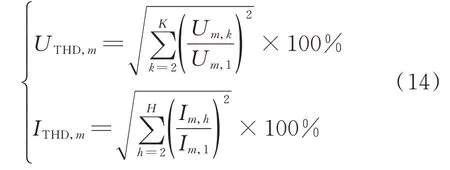
4.1.2 计算和仿真结果对比分析

基于式（3）可求得不平衡供电条件下的三相6 脉波整流电路直流电压,附录B 图B1 给出了Case 1 至Case 4 直流侧谐波电压的计算和仿真结果频谱对比图。由图B1 可知,在不平衡电压分量作用下,直流电压中除了包含6k次特征谐波,还包含6k±2 次偶次谐波,将造成每个周期内的6 个脉波幅值呈现不同程度的变化。

采用所提模型可得交流电流,附录B 图B2 为A相电流的计算和仿真结果对比图,图中ITHD,A表示仿真结果A 相电流THD,可看出模型计算结果和仿真结果吻合程度高。图3 进一步对比了Case 1 至Case 4 的交流电流仿真及计算结果频谱,可知所提模型能够对6k±3 次谐波分量进行准确估计。

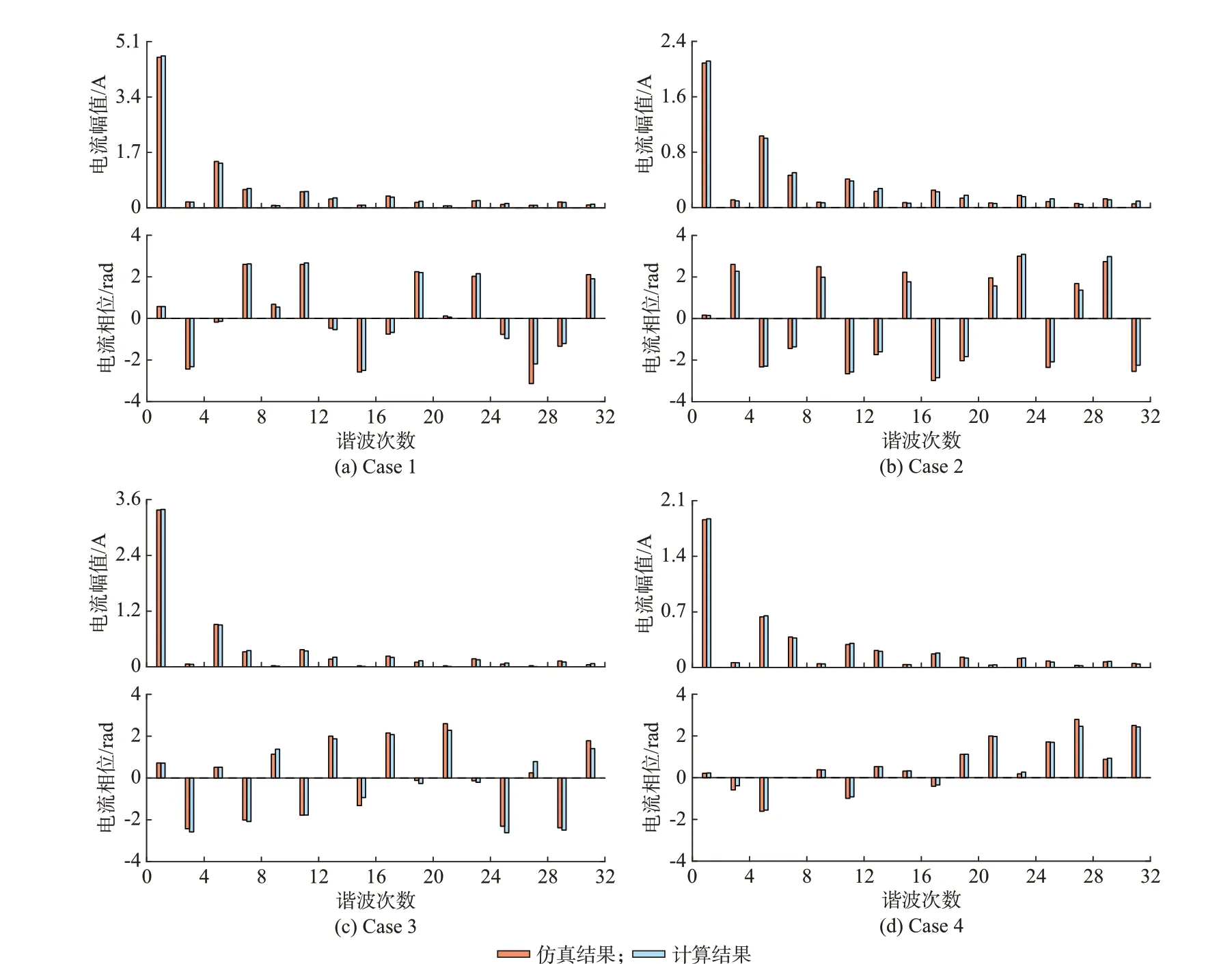
图3 交流电流计算及仿真结果频谱图Fig.3 Frequency spectrums of calculation and simulation results of AC current

为进一步量化所提模型的准确程度,定义相对误差指标εRE衡量模型的准确程度,同时定义非特征谐波总含量ITHDN及h次谐波含量IHD,h如下：

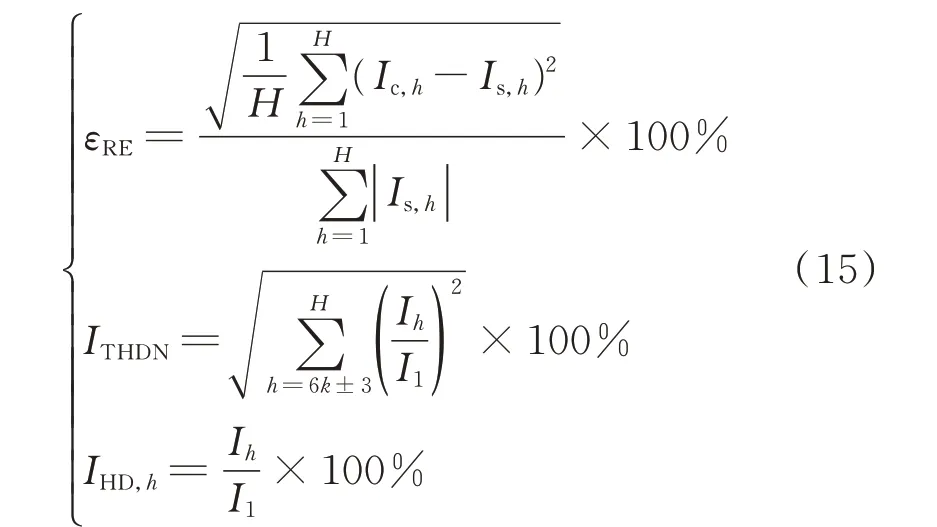
式中：Ic,h和Is,h分别为h次谐波电流分量的计算和仿真结果的幅值；I1和Ih分别为基波和第h次谐波电流幅值。

以下对比分析HCM 以及工程中较为常用的恒流源模型和诺顿等值模型的相对误差［17］,同时比较了未考虑不平衡分量时HCM 的相对误差,各模型的相对误差εRE如表2 所示。

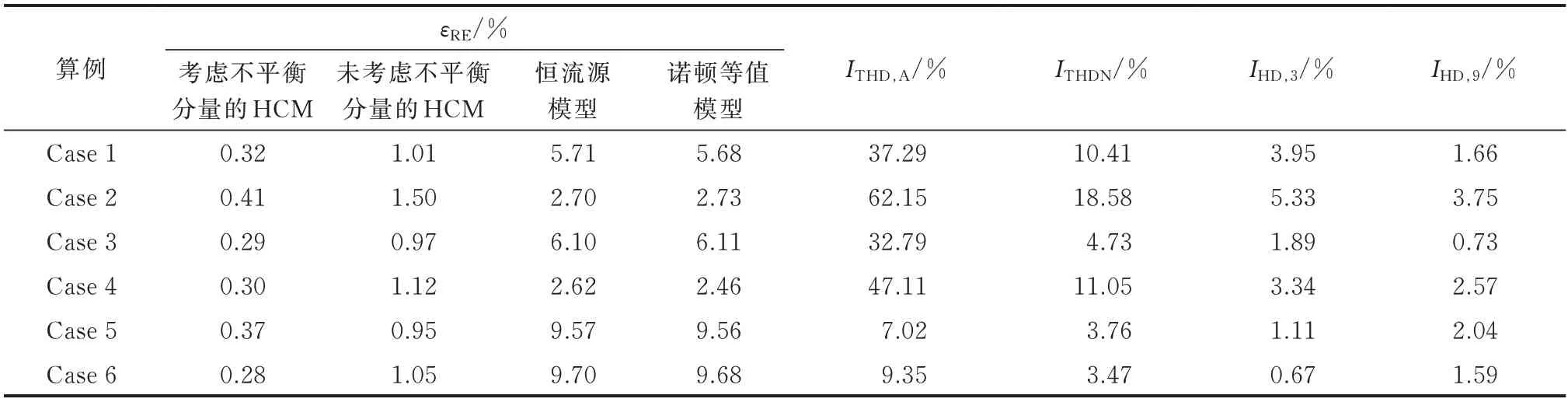
表2 计算及仿真结果相对误差对比Table 2 Comparison of relative errors between calculation and simulation results

由表2 中εRE对比可知,所提模型精度较高且能维持相对稳定,各频次谐波之间耦合作用对模型精度影响明显,不能忽视谐波电压与不同频次谐波电流相互作用的影响。当谐波耦合模型中未考虑不平衡分量作用时,由于无法有效评估非特征谐波含量,模型相对误差随着非特征谐波含量的增加而提高。为进一步明确不平衡电压分量与各频次谐波电流之间的耦合关系,以基波电流和基波电压的导纳幅值为基准,对比了Case 3 和Case 4 的附加谐波耦合导纳矩阵ΔY+m和ΔY−m的幅值,如附录B 图B3 所示。可以看出,各次谐波电压、电流之间具有较强的耦合特性,甚至存在谐波电压与不同频次谐波电流之间互耦合作用强于谐波电压与对应频次谐波电流自耦合作用的情况。

此外,表2 给出了电网侧谐波含量,各算例非特征谐波均具有较高含量,所提模型可进行有效衡量。通过对比,采用12 脉波整流方式虽然一定程度上可抑制3 倍频谐波含量,但较多应用于高压直流输电中［4-6］,电流较大时非特征谐波电流仍不可忽视。以目前国内±500 kV 高压直流输电工程为例,如三常、三广、三沪、贵广Ⅰ/Ⅱ回直流工程等,额定电流为3 000 A,Case 5 和Case 6 设置条件下电网侧3 次谐波幅值将分别达到33.3 A 和20.1 A,9 次谐波幅值将分别达到61.2 A 和47.7 A,而电网侧IHD,5分别达到2.42% 和0.77%,IHD,7分别达到0.64% 和0.38%。另外,目前已有基于晶闸管的超高压直流输电的研究［1］,其额定电流已高达5 500 A,在此情况下,非特征谐波的影响更不容忽视,非特征谐波电流必须得到有效治理。

为评估各频次非特征谐波含量,表3 给出了以3 次谐波为基准,各算例6k±3 次谐波含量的占比。可以看出,对于三相6 脉波整流器,非特征谐波中3 次谐波含量最高,而对于12 脉波整流器,9 次及15 次谐波成为非特征谐波中的主要成分,非特征谐波在不同整流电路中呈现出不同的特点。

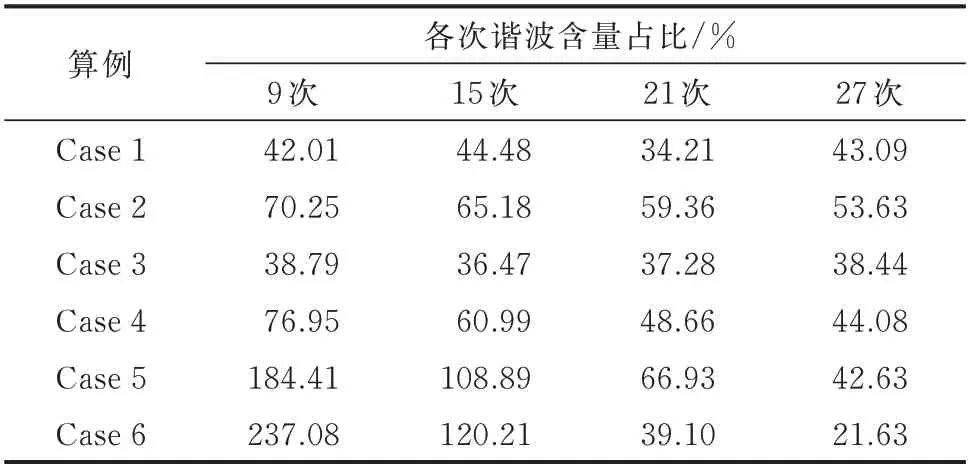
表3 非特征谐波含量占比Table 3 Proportion of non-characteristic harmonic

由此,应用所提模型,不仅弥补了现有模型难以分析非特征谐波的不足,且仅需计算一次谐波耦合导纳矩阵便可适应供电电压动态变化。另外,在不平衡供电条件下,所提模型不仅可有效评估6k±3 次非特征谐波含量,也可为移相变压器及电网的谐波抑制措施提供参考。

4.1.3 不同运行工况下结果的对比分析

进一步,以Case 3 和Case 4 为例,分析不平衡电压分量对相对误差及3 次谐波含量的影响,分别改变Case 3 中B 相和Case 4 中C 相的不平衡分量幅值和相角,计算及仿真结果相对误差εRE及3 次谐波含量IHD,3的变化趋势如图4 所示,其中：Kamp为幅值变比；Dang为相角变化量。

由图4 可知,3 次谐波含量随着不平衡程度的加剧逐步提高,且与谐波电压相角也有关。当不平衡分量发生改变时,所提模型相对误差仍能保持稳定,验证了所提模型对复杂运行工况的适用性。

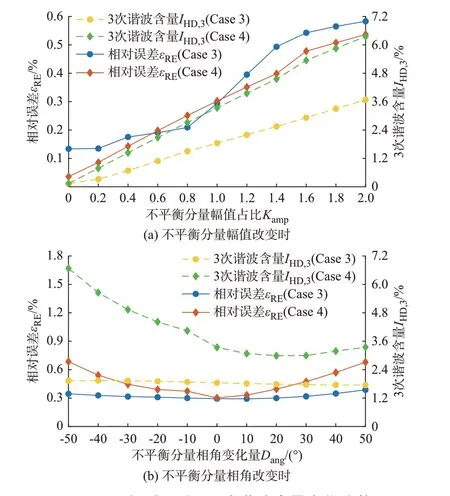
图4 相对误差及3 次谐波含量变化趋势Fig.4 Change trend of relative error and 3rd harmonic content

此外,根据上述对比结果可以看出,触发角α对相对误差也存在影响。为验证触发角α对模型准确性的影响,在保证其他参数不变的情况下,附录B 图B4（a）给出了随触发角α变化的相对误差εRE的变化趋势。由该图可以看出：当触发角大于20°时各算例相对误差随着触发角的增大而增加；当触发角小于20°时,由于电压偏差对触发及关断时刻的影响减弱,相对误差呈现下降趋势；当触发角大于60°时,直流侧电流出现断续,相对误差明显增加。

为提升所提模型应对不同工况的通用性,通过判断交流电流半个周期内电流值是否存在异号,可有效确定直流侧电流连续和断续状态。进一步,将电流断续状态下的模型进行修正,相对误差εRE的变化趋势如图B4（b）所示。可以看出,在触发角变化时,所提模型相对误差仍具有较高的精度,验证了所提模型的有效性并提升了模型的通用性。

4.2 实验验证

4.2.1 三相6 脉波整流电路实验验证

搭建三相6 脉波整流电路实验平台,验证所提模型的准确性,如附录B 图B5 所示,采用可编程交流电源Chroma 61860 供电,直流侧接入阻感负载,电阻R=153.5 Ω,电感L=6.3 mH,实验电路中晶闸管型号为Semikron SKKT 57/16E。采用高压差分探头Tektronix P5200 和交流电流钳表Fluke i5s 对实验电压和电流进行测量,并通过NI USB-6229 对数据进行采集,采样频率为12.8 kHz。实验中A、B、C 三相独立控制,A 相基波电压有效值为220 V,三相电压不平衡度为2.39%,最高谐波频次为31 次。

在基波和谐波电压相同相位供电情况下,三相电压THD 分别为5.09%、6.98%、4.60%,3 次谐波含量分别为2.54%、1.68%、1.13%。基波和谐波电压不同相位供电情况下三相电压THD 分别为5.09%、6.80%、4.58%。测量电压求得电压平衡分量及不平衡分量后,利用谐波耦合导纳矩阵模型,可求解得到考虑电压不平衡及谐波差异情况下的交流侧各次谐波电流,模型计算结果和实验结果的相对误差εRE以及未考虑不平衡电压分量的HCM 特征谐波电流计算和实验结果的相对误差εRE0如表4 所示,同时给出了3 次谐波电流含量IHD,3。

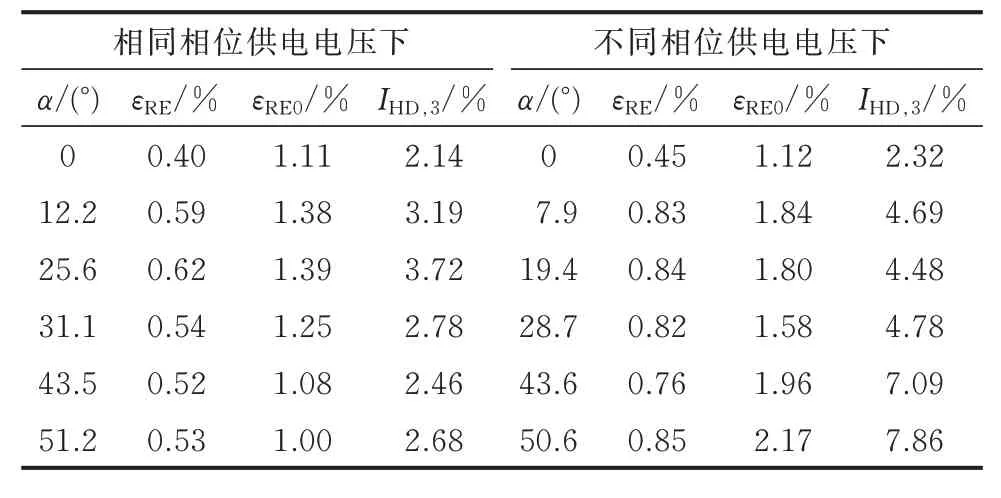
表4 三相6 脉波整流电路计算及实验结果相对误差Table 4 Relative error of calculation and experiment results of three-phase 6-pulse rectifier circuit

在不同供电电压及触发角情况下,所提模型相对误差相对稳定且能保持较高的精度,但未考虑不平衡电压分量时HCM 的相对误差随非特征谐波的增加有所提高。另外,各场景中3 次谐波含量均超过2%,最高达到7.86%,在此情况下,所提模型在衡量非特征谐波含量时具有较为明显的优势。在不同相位供电情况下选取2 种触发角,进一步对比了交流电流的幅值和相角,如图5 所示。

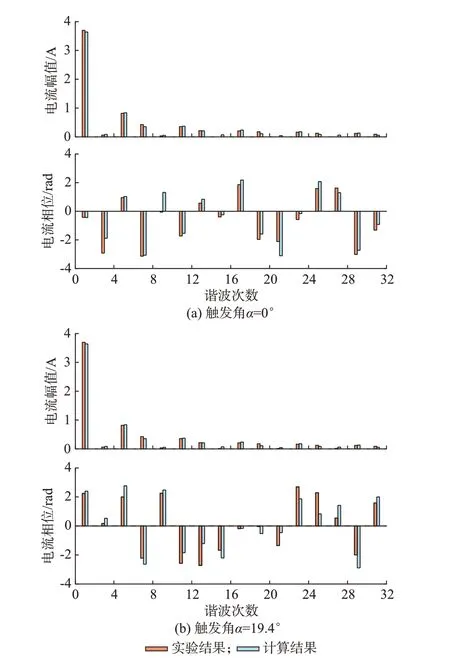
图5 不同相位供电电压下电流频谱对比图Fig.5 Comparison of current spectrums with different phases of power supply voltage

根据对比结果可知,实测数据中交流电流中除包含6k±1 次特征谐波分量外,还包含6k±3 次非特征谐波分量,在考虑不平衡分量影响后,采用本文所提模型能够较为准确地计算出特征谐波和非特征谐波的含量及其相角,验证了模型的准确性。进而可将考虑不平衡工况的HCM 应用于整流装置的谐波分析中,在不平衡系统谐波潮流计算及谐波责任划分等领域,能有效降低谐波计算的复杂度。

4.2.2 12 脉波整流电路实验验证

搭建12 脉波整流电路实验平台,验证所提扩展模型的准确性,实验平台照片如附录B 图B6 所示。该实验平台在三相6 脉波整流电路实验平台基础上,增加一组相同的三相6 脉波整流电路,晶闸管型号一致,整流电路交流侧分别与星形/星形和星形/三角形接法的变压器相连,KT=1,变压器容量均为3 kVA。直流侧采用图2 中接法串联阻感负载,电阻R=304.5 Ω,电感L=6.3 mH,其余实验条件与三相6 脉波整流电路实验一致。

实验设置A、B、C 三相独立控制,A 相交流输入基波电压有效值为110 V,并同样设置相同相位及不同相位2 种供电情况,不平衡度及谐波含量均与三相6 脉波整流电路实验保持一致。表5 给出了所提模型计算结果和实验结果的相对误差εRE,以及未考虑不平衡分量的HCM 的特征谐波电流计算结果和实验结果的相对误差εRE0、3 次谐波电流含量IHD,3。根据该结果可验证所提模型的有效性。

表5 12 脉波整流电路计算及实验结果相对误差Table 5 Relative error of calculation and experiment results of 12-pulse rectifier circuit

以不同相位供电电压下触发角α=6.7°时的实验结果为例,对比实验及计算所得交流电流的幅值和相角,如附录B 图B7 所示。根据频谱可知,不平衡供电条件下6k±3 次及5 次、7 次等非特征谐波均不能得到消除,在考虑不平衡分量影响后,采用所提模型能够更为准确地计算出特征谐波和非特征谐波的含量,验证了模型的准确性。

5 结语

本文提出了三相6 脉波整流器不平衡供电条件下的频域HCM,并基于此将模型扩展至多脉波整流电路,以12 脉波整流器为例建立了不平衡工况下的多脉波整流电路HCM,有效地明确了三相供电差异时整流电路的谐波产生特性。模型能够适应更为复杂的电网供电情况,直观体现了特征谐波和非特征谐波分量与谐波电压之间的耦合关系,且通过采用附加谐波耦合导纳矩阵的形式,分析了不平衡电压分量的影响。通过对运行过程中可能出现的电流断续情况进行判断并对此进行修正,提升了模型的通用性。本文研究可为非理想供电情况下基于三相6 脉波整流电路的整流装置的谐波耦合分析提供参考,进而指导整流装置的设计和研究,为相关谐波治理措施的提出及设备的选型提供参考。考虑到整流器直流阻抗特征也会对谐波特性造成影响,后续将对此进行研究以进一步扩展模型的应用范围。

本文研究得到山东大学青年学者未来计划项目(2016WLJH07)的资助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。