基于鲁棒模型预测控制的配电网供电恢复策略

谢云云，杨正婷，蔡 胜，王 栋，陈 汹，邹 云

（1. 南京理工大学自动化学院,江苏省南京市 210094；2. 国网淮安供电公司,江苏省淮安市 223002；3. 南瑞集团有限公司（国网电力科学研究院有限公司）,江苏省南京市 211106）

0 引言

飓风、洪水、雷暴等恶劣天气会引起大量输电设备故障,造成大范围用户停电,严重影响配电网的运行。近年来,随着微网（MG）技术的不断发展,越来越多的MG 接入配电网中,使配电网逐渐呈现出多源主动的特征,给配电网运行策略的制定带来了新的机遇。含MG 的配电网在发生故障后,不仅能够通过配电网络重构减少停电范围［1］,在网架重构无法恢复的区域内,还可以利用MG 内分布式电源（DG）向配电网提供部分功率,对重要负荷供电［2-5］,从而提高整个配电网的弹性。

国内外许多学者已经对含有可再生能源或者MG 的配电网供电恢复策略进行了研究。其中,文献［3-5］以一个时间断面上的DG 确定性出力对配电网供电恢复进行优化。考虑到MG 内的DG 出力和配电网中负荷需求具有不确定性,其实际出力值与预测值之间存在预测误差,按确定性处理难以保障配电网系统的功率平衡,严重时可能超出安全限制,且难以保障整个配电网运行过程中的功率平衡。为了降低DG 和负荷需求不确定性对配电网运行安全性的影响,有学者在配电网供电恢复策略研究中使用蒙特卡洛模拟方法将负荷需求、DG 出力的不确定性建模为场景集［6-7］,也有学者采用概率密度函数建立不同时段光伏出力的离散概率模型,基于机会约束规划模型优化弹性运行方案［8-9］,亦有学者对整个恢复过程进行建模,建立滚动模型或多阶段供电恢复模型,动态更新系统状态［7,10］。

上述方法对可再生能源出力的不确定性有一定的适应性,然而获取较为准确的概率分布函数较为困难。相比随机规划方法,鲁棒优化（RO）是一种基于区间理论的建模方法,仅需预先知道不确定性参数波动范围即可。文献［11］提出了基于鲁棒优化的弹性运行优化模型,该模型可以在“最坏”DG 输出的情况下向尽可能多的负荷供电。然而,该方法仅考虑了一个时间段中DG 出力的不确定性,忽略了多个时间段中系统状态的相关性。

基于此,本文提出基于鲁棒模型预测控制（RMPC）的含MG 配电网的供电恢复策略。基于模型预测控制（MPC）理论［12］,对MG 内可再生能源出力和负荷需求进行多时步预测,每次做恢复决策时考虑多个时步,但仅下发后一个时步的恢复计划,在下一个恢复周期到来时,重复上述过程进行滚动优化,实现反馈校正。同时,基于鲁棒优化理论,将可再生能源出力用区间值的方法进行建模,建立在可再生能源出力波动范围内系统安全约束均能满足的多时步鲁棒优化模型。并运用强对偶理论,将双层鲁棒优化模型建模为混合整数二次约束规划问题。

1 含MG 的配电网供电恢复框架

当恶劣外部环境造成配电网内多处物理故障时,配电网中MG 可以利用其中的可再生能源为配电网提供能量,支持重要负荷的持续运行。目前在全球多个国家已经建立了含MG 的实际配电网［6,9,13-14］。配电网中的MG 一方面可以与网架重构配合减少停电范围,另一方面可以向孤立负荷供电,减小停电负荷量。但由于可再生能源出力的不确定性,含MG 的配电网负荷恢复的挑战在于在满足任何操作约束的情况下保证供需之间的功率平衡。

本文提出了基于RMPC 的弹性运行策略,通过将可再生能源出力建模为区间值,并考虑多个时间段之间配电网系统状态的相关性来最大化供电恢复负荷量,其原理如图1 所示。

图1 基于RMPC 的配电网弹性运行原理Fig.1 RMPC-based principles of elastic operation for distribution network

MPC 的原理如附录A 图A1 所示,其思想是在当前k时步,考虑系统未来有限时段状态,使用当前时步测量值和预测模型,通过控制约束和目标函数的极小化,得到当前和未来有限时段的最优控制［15］。而在k+1 时步,利用k时步控制后的测量数据重复这一优化过程。时步t=k将时间区域划分为2 个部分,左侧为过去实际输入和输出,右侧为将来预测输入和输出。在k时步,基于当前测量值优化求 得Np步 控 制 变 量 Δu={Δu(k|k),Δu(k+1|k),…,Δu(k+Np|k)},以满足预测时域k+Np的目标状态。每个时步只执行N个控制变量中的第1 个控制变量Δu(k|k),在k+1 时步重复上述过程,进行滚动优化。

本文方法通过协调MG 中可控DG、储能系统（ESS）以及配电网中开关优化配电网的供电范围。ESS 用于减轻配电网的功率波动,分段开关和联络线开关操作可以改变系统网络拓扑,负载节点的自动开关可以控制恢复的负荷量。数据采集系统将从配电网中采集到的ESS 的电量、各开关的状态以及DG 出力和负荷需求的预测值送到RMPC 计算模块。然后,根据系统预测模型进行优化,求解优化模型从而获得可控机组的最佳功率参考值以及自动开关的一系列动作命令。将第1 个时步的控制命令发送到传输线和负载节点中的每个单元和远程控制开关（RCS）,实现最大的负荷供电量。

2 基于RMPC 的配电网供电恢复模型

2.1 预测模型

1）可再生能源

本文考虑了基于逆变器并网的DG［16-17］,其能够响应电网的调度指令。同时,本文考虑了DG 输出的不确定性,可以将其描述为凸区间和有界区间。以风机为例对配电网中可再生能源进行建模,其出力的预测区间可表示为：

风机出力允许区间应是风机出力预测区间的子集,但是在实际配电网系统中,由于ESS 装置的存在,某些时段可用的风机出力不能被完全吸收。因此,允许风机出力的下限应该小于等于预测出力的下限,则风机允许出力约束如下［18］。

2）ESS 装置

ESS 装置通过充放电吸收或发出有功功率参与配电网的弹性运行,因此,ESS 装置的有功出力为控制变量,其预测模型如下：

2.2 优化模型

2.2.1 目标函数

本文以总的运行成本最小为优化目标,包括联络开关操作成本、MG 内以及配电网中负荷损失成本和可控机组出力成本,具体为：

式（5）中,第1 项表示k时步联络线开关对比当前时步联络线开关状态的操作成本,第2、3 项分别表示配电网内和MG 内的负荷削减成本；最后1 项表示微型燃气轮机的发电成本,假设可再生能源和储能的发电成本忽略不计。

2.2.2 约束条件

基于MPC 的配电网弹性运行模型包括潮流约束、MG 外送功率约束、拓扑结构约束、线路约束、ESS 约束等,在预测周期内每一个时步都需要满足这些约束条件。

1）MG 外送功率

本文MG 内DG 有光伏、风机和燃气轮机,燃气轮机是可控机组,其有功和无功出力是决策变量。假定只有燃气轮机可以发出无功功率,则MG 外送的有功和无功功率分别为：

5）电压安全约束

根据配电网潮流方程,建立电压安全约束。

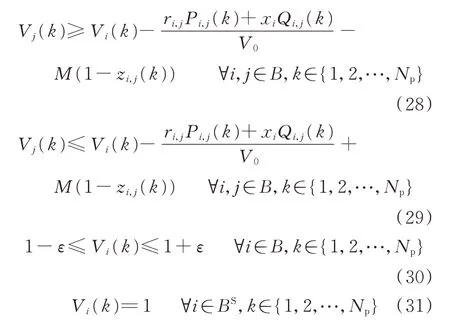
式中：Vj(k)和Vi(k)分别为母线j和i在k时步的电压；V0为与主网相连的母线电压；ri,j和xi分别为线路上的电阻和电抗；ε为电压的松弛变量,通常设定为0.05。当zi,j(k)=1 时,电压安全约束为线性化的配电网潮流方程,当zi,j(k)=0 时相应的约束失效。

6）支路容量约束

2.3 模型求解

2.3.1 求解思路

基于MPC 的配电网弹性运行的抽象鲁棒优化模型简述如下。

约束式第1 行的约束条件含有不确定变量,鲁棒优化模型式（33）难以求解,而min-max 问题的根本在于当不确定量的不确定性最大时,约束能够满足且目标函数值最小。因此,在生成不确定参数的最坏情况下保证系统的安全约束得以满足,即可将上述约束式第1 行转化为：

2.3.2 基于RMPC 的配电网弹性运行模型求解

2.2 节中将基于RMPC 的配电网弹性运行模型建模为双层的鲁棒优化模型,根据2.3.1 节简单鲁棒优化模型的求解方法,运用强对偶理论将两层的鲁棒优化模型转化为单层的混合整数二次规划模型,从而方便求解。

在原始的两层鲁棒优化问题中,式（33）即为双层优化问题。引入对偶乘子εi,w(k),则相应的对偶问题为：

考虑风机出力不确定性的最终的混合整数二次规划单层弹性运行模型为：

上述的单层混合整数二次规划模型（式（40））可以采用广泛应用于电力系统运行优化的商业软件CPLEX 进行求解,以提高寻优效率。

3 算例仿真

3.1 仿真场景

本文采用修改后的69 节点配电系统进行仿真验证,如图2 所示,详细的参数可以参考文献［22］。假设所有的MG 拓扑结构相同,包括1 台风机、1 台微型燃气轮机、1 个光伏电站和1 个能量存储系统,其功率分别设为100 kW、250 kW、50 kW 和5 kW,ESS 的容量设为250 kW ⋅h。所有设备均简化为连接在1 个母线上。

图2 含有MG 的配电网测试系统Fig.2 Testing system of distribution network with MGs

负荷分为2 类：70%的重要负荷和30%的常规负荷,其中,母线1 至14、41 至56、60 至61 所连负荷为普通负荷,其余母线所连负荷为重要负荷。假设配电网中负荷和DG 预测功率如表1 所示,并且所有节点的功率变化相同。

表1 负荷和电源功率变化倍数Table 1 Multiples of power variation for load and supply

由于一次严重的天气事故会导致配电网多处故障,因此,本文设想有5 处故障任意分布于配电网中,如图2 所示。假设故障发生在高峰时刻17：15并持续2.25 h 至19：30。假设风电出力预测的时间步长是15 min,后续分析中以15 min 作为MPC 和RMPC 方法的时间步长。

3.2 算例分析

3.2.1 有无MG 对供电恢复策略的影响分析

本节以2 个控制时步为例,分析配电网中有无MG 对供电恢复结果的影响。通过设置式（6）和式（7）的MG 有功和无功出力为0,可以得到不含MG的配电网供电恢复成本,见附录A 图A2,并与含有MG 的配电网供电恢复成本进行对比,如表2 所示。

表2 有MG 与不含MG 的供电恢复结果对比Table 2 Comparison of power supply restoration results with and without MGs

由附录A 图A2 和表2 可以看出,含有MG 的配电网供电恢复成本低,总恢复负荷量更大,而不含MG 的配电网供电恢复成本高,且恢复了更少的负荷。这是因为含有MG 的配电网在供电恢复时,不仅通过网络重构的方法为负荷恢复提供了电能,MG 内的风机、光伏、储能电源和燃汽轮机也为配电网恢复提供了电能支持,故恢复负荷量更多,而负荷缩减会增加恢复成本。因此,含有MG 的配电网恢复成本更低,与传统不含MG 的配电网供电恢复方法相比,该方法能够更有效地进行供电恢复。以第4 个时步为例,有无MG 时供电恢复拓扑见附录A 图A3 和图A4,负荷恢复结果如表3 所示。

表3 有无MG 供电恢复负荷对比Table 3 Comparison of power supply restoration loads with and without MGs

3.2.2 控制时步数参数分析

本节为了讨论基于RMPC 的不同控制时步数对供电恢复结果的影响,分别假设控制时步数为2、3、4,每个时步的控制时域为15 min,不同的控制时步数对恢复结果的影响如图3 和表4 所示。

图3 不同预测时步数的恢复成本对比Fig.3 Comparison of restoration costs with different prediction time steps

表4 不同预测时步数下的恢复结果对比Table 4 Comparison of restoration results with different prediction time steps

如图3 和表4 所示,分别对比了单时步鲁棒优化和基于RMPC 的多时步供电恢复策略对恢复结果的影响,可以看出基于RMPC 的供电恢复策略选用2 个时步进行恢复时不仅恢复负荷更多,恢复成本也更低。可以看出,控制时步数并不是越大越好,如果预测时步数过大,则DG 出力的预测误差会增加,反而使得恢复策略效果降低,也会带来计算负担。因此,基于RMPC 的主动配电网供电恢复模型需要选择适合的控制时步数才能更好地发挥RMPC 方法在配电网供电恢复中的优越性。

3.2.3 ESS 容量参数分析

为了讨论ESS 的容量对配电网供电恢复结果的影响,本节以2 个时步数为例,假设ESS 容量分别为250 kW ⋅h 和500 kW ⋅h,ESS 的容量大小对配电网供电恢复结果的影响见表5 和附录A 图A5。

表5 ESS 容量大小对供电恢复的影响Table 5 Impact of different capacities of ESS devices on power supply restoration results

从附录A 图A5 可以看到,当ESS 的容量为500 kW ⋅h 时,相比于ESS 的容量为250 kW ⋅h,不仅恢复成本更低,恢复负荷也更多。这主要是因为当MG 内ESS 装置可以提供更多能量时,即可减少燃气轮机的出力,而ESS 装置出力不计成本,因此,当ESS 的容量更大时,供电恢复结果更优。

3.2.4 控制方法对比分析

为了验证所提方法的有效性,分别将RMPC 方法与确定性方法（单时步）、RO 方法、基于MPC 的确定性方法和随机优化方法进行对比。RO 方法考虑可再生能源出力的预测误差,根据其波动范围建立单时步RO 模型。基于MPC 的确定性优化方法则忽略了可再生能源的出力误差。随机优化方法则针对主动配电网的弹性运行问题建立随机优化模型,并通过蒙特卡洛模拟处理可再生能源的不确定性。在用鲁棒优化方法进行恢复时,主要考虑风机出力误差,假设风机出力波动范围为10%。

仿真结果如图4 和表6 所示,通过5 种方法的恢复结果对比可以发现,基于MPC 的确定性弹性运行方法总恢复负荷更多,恢复成本更小。这是因为基于MPC 的确定性弹性运行方法忽略了风机预测出力误差,认为实际风机出力等于其预测值,而基于RMPC 的弹性运行方法充分考虑了风机出力的不确定,考虑了风机出力波动的最坏情况。

表6 5 种方法的优化结果对比Table 6 Comparison of optimal results of 5 methods

图4 5 种方法的恢复负荷对比Fig.4 Comparison of restoration load of 5 methods

本文采用功率安全水平来衡量不同方法的效果。功率安全水平用配电网所提供的有功出力（包含MG）与配电网内恢复的负荷有功功率之差表示。当风机出力波动最大时,不同方法的功率平衡安全水平分析结果如图5 所示。从图5 中可以看出,在实际风机波动最坏的情况下,确定性优化方法、基于MPC 的确定性优化方法和随机优化方法在安全线以下,也就是说这3 种方法在风机出力波动最大时极有可能违反功率平衡安全约束,而RO 和RMPC优化方法则始终在安全线以上。基于RMPC 的主动配电网弹性运行方法尽管无法部分恢复负载,但是其相应的恢复策略始终满足安全约束。因此,RMPC 方法在保证了MG 供电安全的前提下,可以为负荷提供更多的功率支持,具有更小的代价。

图5 最坏场景下5 种方法的安全水平对比Fig.5 Restoration safety level of 5 methods in worst-case fluctuation scenarios

4 结语

由于MG 内可再生能源出力的波动性会影响含MG 配电网的运行安全,因此,本文提出了基于RMPC 的含有MG 的配电网弹性运行策略。该方法考虑了可再生能源出力波动的最坏情况,建立鲁棒优化模型,然后利用对偶理论将鲁棒优化模型进行转化,并用滚动预测模型考虑了多个时间段之间配电网状态的相关性。仿真结果表明,本文方法能够在保证配电网安全的条件下,尽可能多地为配电网内负荷供电,同时降低总操作成本。

基于RMPC 的供电恢复方法的一个关注点是,随着可再生能源（如风能）出力预测误差变大,该算法可能变得过于保守,不必要地减少了风力发电,因为对于每种可能的风能输出情形（即使概率很小的情形）都可以保证安全性约束。因此,需要进一步研究的方向是根据给定风况的概率来改善预测数据的处理,以在鲁棒性和经济性之间取得平衡。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。