考虑系统参数不确定性的谐波谐振监测点优化配置方法

蒋海玮，徐永海，何志轩，陶 顺，常 潇，王金浩

（1. 新能源电力系统国家重点实验室（华北电力大学）,北京市 102206；2. 国网山西省电力公司电力科学研究院,山西省太原市 030001）

0 引言

电能质量监测是电能质量问题得到分析和控制的重要环节和前提条件［1-3］。但由于电力系统中节点众多、拓扑结构错综复杂,若在系统中所有节点均安装电能质量监测装置将耗费巨大成本［4］。因此,在经济条件允许的范围内合理配置有限监测点,以实现对相关电力扰动观测能力的最大化是解决上述问题的关键。为此,国内外学者围绕电压暂降和谐波监测点的优化配置问题开展了较多研究［4-7］。

除了对电压暂降和谐波的关注外,电力系统中的并联谐波谐振同样引起了广泛关注［8-10］。并联谐波谐振现象常表现为系统中某些节点的谐波过电压,进而造成设备绝缘老化或击穿、保护装置损坏以及电压互感器烧毁等,严重危害到电力系统的正常运行。文献［8］的研究表明,系统节点导纳矩阵趋于奇异是并联谐波谐振现象的真正原因,对谐波谐振的分析可以转化为对谐波谐振关键模态的分析,应用谐波谐振模态分析（harmonic resonance mode analysis,HRMA）法可以识别系统潜在的谐波谐振频率,并对各节点的谐振可观性进行有效评估。

考虑到谐波谐振问题具有严重的危害性,谐波谐振评估方法较早便得到研究,但有关谐波谐振监测点优化配置方法的研究却较晚。文献［11］报道了旨在监测系统潜在谐波谐振状态的电能质量监测点优化配置方法。该优化配置方法在仅考虑并联电容器组完全投入或完全退出对谐波谐振潜在影响的前提下,基于HRMA 法构建了谐振监测矩阵（resonance monitoring matrix,RMM）,以描述各母线的谐振可观性,进而基于RMM 建立了以最少监测装置数实现谐振完全可观的监测点优化配置模型［11］。

然而,目前基于RMM 的谐振监测点优化配置方法仍存在一些不足。一方面,在分析谐波谐振问题时,除需考虑并联电容器组取值的改变外,还应考虑发电机、变压器、输电线路以及负荷等元件参数取值的随机性［12］。充分考虑系统不同类型元件参数取值的随机性更容易挖掘系统客观存在的不同潜在谐振现象［12-13］。因此,文献［11］在仅考虑并联电容器组完全投入或完全退出场景下建立的RMM 无法准确刻画监测点配置方案对系统潜在谐振现象的可观性。另一方面,现有优化配置方法的初衷是以最少的监测点实现谐振现象的完全可观［11］,但在谐振完全可观的高要求约束下,即使以装置数目最少为目标寻优,所得配置方案需要的监测装置数依然可能会超过投资方短期内最多能够提供的装置数,从而最终导致配置方案在实际工程中难以应用。

谐波谐振监测点的优化配置对有效监测实际系统中的谐振现象具有重要意义,从而为谐波谐振问题的分析与治理奠定了良好基础。鉴于目前关于谐波谐振监测点的优化配置方法研究尚处于初级阶段,本文提出了一种考虑电力系统不同类型元件参数取值不确定性的并联谐波谐振监测点优化配置方法。本文的主要贡献为：①基于系统参数随机模型,应用HRMA 法和蒙特卡洛法,构建了概率性谐振监测矩阵（probabilistic resonance monitoring matrix,PRMM）,用于刻画系统参数取值随机变化条件下各节点对不同潜在并联谐振现象的可观性；②定义并量化了用于描述任意配置方案谐振监测能力的谐振可观性指标（resonance observability index,ROI）,并在此基础上提出了可观性-成本权衡因子,用于描述谐振可观性和投资成本经济性之间的权衡关系；③提出了一种谐波谐振监测点的优化配置方法,该方法可以在确保配置方案所需监测装置数满足投资成本限定的条件下,实现谐波谐振可观性和投资成本经济性之间的协调优化。

1 HRMA 法

HRMA 法可以依据节点导纳矩阵的特征值来辨识并联谐波谐振（后文简称为谐振）频率,并通过特征向量评估各节点的谐振可观性［8］。

假设Yf为系统在频率f处的节点导纳矩阵,则节点电压Vf与节点注入电流If之间的关系如式（1）所示。为简化符号,后文将省略下标f。

由于各特征值的倒数是以阻抗为量纲的物理量,故称其为模态阻抗（Zm）。通过式（4）可以看出,若节点导纳矩阵的第k个特征值（λk）的模值为0 或者较小时,很小的模态电流（Jk）也将导致很大的模态电压（Uk）。另外,由于向量J与U间已解耦,故Jk不会影响除Uk外的任何模态电压,这意味着谐波谐振实际上是对应某个特定的模态而发生。此时,这个与谐振有关的最小特征值λk被称为关键特征值,λk的左、右特征向量被称为关键特征向量。λk模值的倒数zk=|λk|−1为关键模态阻抗,zk对应的频率为谐振频率（fm）,zk与fm共同定义了谐波谐振的关键模态（后文简称为谐振关键模态）［12-13］。为获得确定参数下待研究频率范围内的全部谐振关键模态,可作出最大模态阻抗随频率的变化曲线,曲线各极大值点即对应各谐振关键模态［8］。

根据模态电压公式U=TV,节点电压与模态电压间存在如下关系：

因Uk的值远大于其他模态电压值,所以存在上式的近似关系。

式（5）表明模态电压Uk对实际电压的贡献可以用关键左特征向量Lk=［L1k L2k…LNk］T来表征,该向量内某元素的模值越大,其对应的节点谐波电压被放大的程度就越高,即系统谐振关键模态的可观性越强,在该位置安装电能质量监测装置就越容易监测到系统所处的谐振状态。

2 考虑系统参数随机性的RMM

不同类型元件参数取值的随机不确定性会导致系统客观存在着极为丰富的潜在谐振现象［12］。为有效刻画各节点对系统大量潜在谐振关键模态的可观性,本章将建立系统参数随机模型,并在此基础上应用HRMA 法和蒙特卡洛法提出概率性谐振可观性矩阵（probabilistic resonance observability matrix,PROM）,以及与PROM 相对应的PRMM。

2.1 系统参数随机性建模

发电机等值阻抗、变压器与输电线路参数以及负荷的有功和无功功率均可视为服从正态分布的随机变量［12,14］。对于并联电容器组而言,其投入的容量通常由负荷需要补偿的无功功率决定,因此可不对其单独建立随机模型,即电容器参数样本的取值方式为：首先,根据负荷功率随机模型抽样得到一组负荷有功和无功功率取值,再根据该次抽样得到的负荷有功和无功功率以及提前设定的节点目标功率因数值计算并联电容器组需投入的容量。综上,假设m表示某元件参数（电阻、电感、电容或负荷功率）的随机取值,则各类元件参数的概率密度函数如下所示：

式中：μ和σ分别为元件参数的期望和标准差。

根据3σ法则,各类元件参数将有99.7%的概率出现在区间μ±μδ内,其中δ=3σ/μ×100%。此时,可基于式（6）所示的系统各元件参数概率密度函数,利用蒙特卡洛法抽样得到各元件参数对应的样本矩阵S为：

式中：任意元素st为第t次蒙特卡洛模拟所得各元件参数基准值样本构成的列向量,其中并联电容器组的取值根据负荷功率的抽样值和目标功率因数值计算得出；T为蒙特卡洛模拟总次数。

2.2 PRMM 的建立

由式（5）可知,在某一确定系统参数取值情况下,节点导纳矩阵的关键左特征向量Lk可以表征各节点对某频率下谐振的观测能力。基于此,本文在考虑系统各参数取值具有不确定性的情景下,建立PROM 如下：

式中：分块矩阵Mt表示系统各元件参数基准值按式（7）所示样本矩阵S中的向量st进行取值时,对系统节点导纳矩阵进行HRMA 所得全部归一化关键左特征向量合并而成的矩阵。

Mt的具体表达式如下：

Mt的第j列为第j个谐振关键模态对应的关键左特征向量Lk=[L1k L2k…LNk]T经归一化处理后所得的向量（1≤j≤H,H为谐振关键模态数）,故矩阵Mt中各元素aik,j模值的范围均介于区间［0,1］内,aik,j模值的大小表示节点i对第j个特定谐振关键模态的可观测能力,其模值越接近于1 表示节点i对第j个谐振关键模态的观测能力越强。

为便于后续对配置方案谐振可观能力的量化以及对监测点优化配置模型的建立,本文根据MPROM进一步定义了如式（10）所示的PRMM,即MPRMM=(MPRMM,ij),以刻画各节点能否监测到某谐振关键模态。

式中：τ∈(0,1]为判断某节点能否观测到谐振的阈值。当|MPROM,ij|≥τ时,MPRMM,ij取 值 为1,以 表 示 节点i能观测到第j个谐振关键模态；反之,当|MPROM,ij|＜τ时,MPRMM,ij取值为0,以表示节点i不能观测到第j个谐振关键模态。

鉴于并联谐波谐振监测旨在以系统严重的节点谐波电压放大现象来反映系统当前是否正承受谐振的干扰,故阈值τ的取值越接近于1,通过式（10）就越容易筛选出谐振严重程度更高的节点作为候选谐振监测点。但当τ取为1 时,仅认为谐振电压最大的节点是谐振可观的唯一节点,从而导致实现谐振完全可观配置方案所需的最少监测装置数相比于其他阈值下所需的装置数更多［11］。因此,在实际工程应用中可适当降低τ的取值（如取为0.95）,从而保证在候选监测点同样具有高谐波电压放大程度的情况下降低谐振完全可观所需的最少监测装置数。但目前关于阈值的选择尚未有严格的标准,本文后续不再就该问题做深入探讨。

3 监测点优化配置方法

为在考虑系统参数随机不确定性的条件下,进一步将监测装置数目限定这一重要因素引入谐振监测点优化配置模型中,本章首先根据第2 章构建的PRMM 提出ROI,以描述任意配置方案的潜在谐振观测能力。然后,基于ROI 提出谐振监测点优化配置方法,以确保在配置方案所需监测装置数满足投资成本限定的条件下,实现谐振可观性和投资成本经济性之间的协调优化。

3.1 ROI

对于含有N个候选节点的待配置系统,可定义如式（11）所示的N维监测点决策列向量X=（xi）,以描述某一配置方案的监测装置安装位置。

式中：i=1,2,…,N。

根据配置方案决策向量X和式（10）所示的MPRMM,某决策向量X对应的ROI 值可由式（12）中的αr来表示。

式中：diag（X）表示以X为对角元素的方阵,则MPRMM,X表示将MPRMM中非监测点对应的行置零后所形成的矩阵；max（MPRMM,Xj）表示矩阵MPRMM,X第j列的最大值,则当配置方案内至少存在一个监测点能够监测到第j个潜在谐振关键模态时,max(MPRMM,Xj)取值为1,若没有监测点能够监测到第j个谐振关键模态,则max（MPRMM,Xj）取值为0；F为矩阵MPRMM的总列数,即与样本矩阵S相对应的系统潜在谐振关键模态总数。

由于只要存在一个监测点能够监测到某一谐振关键模态,即可认为系统所处的谐振状态可观,亦即由谐波电流注入所引发的各节点谐波电压放大现象可感知,因此,ROI 能够描述某一配置方案可观测到的谐振关键模态数占谐振关键模态总数的比例。假设PRMM 反映的全部关键模态均可能出现且每个关键模态出现的可能性相同,ROI 即刻画了系统谐振可以被观测到的概率。ROI 值越大,配置方案的系统谐振可观性就越强。

3.2 优化配置基础模型

3.2.1 谐振完全可观条件下的优化模型

为在考虑系统参数随机变化的条件下,确保PRMM 描述的全部F个潜在谐振关键模态均能至少被一台监测装置监测到（即配置方案的ROI 值为100%）且所需监测装置数目最少,此时的优化配置模型可表达为如下形式：

式中：C为各元素皆为1 的F维列向量。

由于式（13）所示的规划问题为典型的0-1 整数线性规划问题,可采用分支定界算法进行求解［15］。

3.2.2 欠量测条件下的优化模型

假设投资方最多能够提供N1台监测装置,实现式（12）所示ROI 值（αr）为100%最少需要N2台监测装置,则当N1＜N2时,说明因监测装置不足无法实现谐振完全可观。针对此欠量测场景,本文提出以确定数目的监测装置实现ROI 值最大化的优化配置模型。该优化模型可以表达为如下形式：

式中：n为任意监测装置数。此时,将n=N1＜N2代入式（14）并求解该优化模型,即可获得欠量测条件下取得最大ROI 值的配置方案。

由于式（14）所示的优化模型为定约束条件下的离散型非线性规划问题,当装置数上限与网络节点数目较少时,尚可采用枚举法列举出全部的种配置方案并计算出各方案的ROI 值,从而对比得出最大ROI 值对应的配置方案；但当网络节点数目较多,且允许安装较多数目监测装置以实现高谐振可观性时,备选配置方案总数的取值很大,枚举寻优法因运算量巨大而难以应用。为此,本文采用一种基于离散粒子群优化（binary particle swarm optimization,BPSO）的人工智能算法进行模型求解［16-17］,该方法对式（14）中定约束条件的处理方式及整个寻优流程见附录A。

3.3 最终配置方案的确定方法

为确定最终配置方案,应首先根据3.2.1 节给出的优化模型确定以最少监测装置数实现ROI 值为100%的优化配置方案,再对资金允许范围内能够达到的最大装置数N1与此方案所需装置数N2进行比较。若N1≥N2,则以此方案作为基准方案；反之若N1＜N2,则说明谐振完全可观无法实现,此时,选择ROI 值最大的配置方案作为基准方案,以尽可能多地观测到系统的潜在谐振现象。

需要注意的是,之所以称上述配置方案为基准方案,是因为与上述配置方案所需监测装置数（记为nmax）和能够实现的ROI 值（记为αr,max）相比,可能存在所需装置数少于nmax但能够实现的最大ROI 值却十分接近于αr,max的配置方案（这一现象将在后文算例中作进一步说明）。因此,可在基准方案基础上进一步权衡配置成本和谐振可观性,选择二者协调最优的配置方案作为最终方案。因此,本文定义了可观性-成本权衡因子（observability-cost trade-off factor,OCTF）,如式（15）中βt所示。

式中：αn,r,max表示与任意监测装置数n＜nmax对应的最大ROI 值。可见,OCTF 描述了监测装置数从nmax减少至n带来的成本收益而导致的ROI 值下降率。

此时,令βt,max(βt,max∈(0,1))表示投资方允许的最大OCTF 值,则最终的协调最优方案可视为在OCTF 值不超过限值βt,max的约束下,取得成本收益最高,即所需监测装置数目最少的配置方案。

综上,在已获得基准方案的情况下,最终配置方案的获取可转化为多次求解式（14）所示优化模型以寻找临界监测点数的迭代形式,即保持式（14）中的目标函数不变,将约束条件中监测装置数n的取值以nmax为起始量逐次减1,从而求解各n值对应的权衡因子βt,n,并对相邻2 个监测装置数对应的OCTF值进行比较,当在逐次运算过程中出现βt,n1≤βt,max＜βt,n2（其中n1=n2+1≤nmax）时则停止运算,最终的协调最优配置方案即为监测装置数为n1时,实现ROI 值最大化的方案。

4 优化配置实现流程

根据上文内容,本文提出的考虑系统参数不确定性的并联谐波谐振监测点优化配置步骤如下。

步骤1：将系统各元件参数视为随机变量,建立各元件参数随机模型,基于各参数的概率分布情况随机抽样T次,得到各随机变量的样本矩阵S=[s1s2…sT]。

步骤2：设频率f∈[fmin,fmax],以Δf为频率间隔计算获得与样本矩阵S中第1 个列向量s1相对应的系统最大模态阻抗-频率曲线。搜索该曲线全部峰值点对应的谐波谐振频率,并计算各谐振频率处的关键左特征向量,从而形成第1 个如式（9）所示的谐振可观性子矩阵M1。

步骤3：重复步骤2,依次建立S中其余T−1 个参数向量st对应的各Mt,并将全部T个Mt合并,形成如式（8）所示的MPROM。

步骤4：设置阈值τ,根据步骤3 所得的MPROM获得如式（10）所示的MPRMM。

步骤5：首先根据决策者的需求设置能够提供的最大监测装置数N1和权衡因子限值βt,max,最后基于3.2 节提出的优化配置基础模型,采用3.3 节中的方法获取谐振监测点的最终配置方案。

综上,图1 给出了本文提出的并联谐波谐振监测点优化配置详细流程。

图1 优化配置流程图Fig.1 Flow chart of placement optimization

5 算例仿真与分析

5.1 测试系统及参数设置

基于附录B 图B1 所示的IEEE 30 节点测试系统验证本文提出的谐振监测点优化配置方法［18］。本 文 随 机 选 取 该 系 统 节 点10、18、21、23、24、26 这6 处含无功负荷节点接入并联电容器组进行无功补偿,并考虑串有4.5%电抗率的电抗器。

各元件基波参数期望值取为元件基准值,其中发电机采用次暂态电抗模型［19］,电抗基准值取为0.25 p.u.；输电线路与变压器采用集中式等效模型,模型中各电阻、电感与电纳参数如附录B 表B1 和表B2 所示；负荷采用应用较广泛的RL 并联导纳模型［11,20］,此时的负荷谐波导纳Y可按照式（16）来计算［20］。

式中：G和B分别为负荷谐波的电导和电纳；P为负荷有功功率；Q为负荷无功功率；h为谐波次数；VL为负荷处的节点电压。有功与无功功率的基准值如附录B 表B3 所示。发电机、输电线路与变压器模型中各参数标准差按照δ=10%选取,负荷的有功与无功功率标准差按照δ=50%选取［12］。抽样过程中,并联电容器组投入容量按照使负荷功率因数提高至0.97 进行计算。

用于模态分析的频率间隔Δf取为0.1 p.u.（频率的单位以系统基波频率的次数为基准）,所研究的谐振频率范围为1～50 p.u.。建立PRMM 过程中的蒙特卡洛仿真总次数取为10 000 次,阈值τ取为0.95。此外,在求解式（14）所示优化模型时,BPSO 算法中的种群规模设置为20,惯性权重取为w=0.8,正向加速系数取为c1=c2=2,最大迭代次数设置为200 次。

5.2 测试系统潜在谐振关键模态及其可观性分析

本节将对测试系统谐振关键模态在Zm-f平面的分布情况及不同关键模态的可观性进行分析,分析过程中分别考虑系统仅存在各电容器组完全投入或完全退出的场景（文献［11］考虑的场景）,以及系统不同类型元件参数取值随机变化的场景（本文考虑的更为接近真实情况的场景）,并对2 种场景所得结果进行对比分析。2 种不同场景下的潜在谐振关键模态分布情况分别如图2（a）和（b）所示。图中红色曲线均为各元件参数取为基准值时的最大模态阻抗-频率曲线,曲线各峰值点代表系统此时不同的谐振关键模态；蓝色圆圈代表系统元件参数取值有别于基准值时的最大模态阻抗-频率曲线峰值点,即系统在某一特定参数取值情况下的各潜在谐振关键模态。其中,图2（a）中各关键模态代表仅考虑文献［11］场景下的系统不同潜在谐振,图2（b）中各关键模态则代表本文考虑场景下的不同潜在谐振。

图2 不同场景下的潜在谐振关键模态分布Fig.2 Distribution of potential resonance critical modes in different scenarios

由图2 可知,在2 种场景下,随着系统元件参数取值的变化,谐振关键模态较基准曲线峰值点所在位置均发生了偏移,这意味着系统潜在谐振的频率和幅值特征发生了改变,但可以很直观地看出,2 种场景下的关键模态分布情况并不相同。当仅考虑各电容器组全部投入或全部退出时,最终搜索到的潜在谐波谐振点大都分布在基准曲线峰值点附近,而当考虑系统不同类型元件参数取值随机性时,搜索到的谐振关键模态的分布范围更加广泛,更能客观反映系统实际运行中的潜在谐波谐振。

但需指出的是,由图2 可见,频率在5～10 p.u.等频段的部分谐振关键模态能够通过文献［11］算法搜索到,但未能通过本文方法搜索到,这是因为谐振关键模态的分布与参与HRMA 的节点导纳矩阵有关,文献［11］仅考虑了并联电容器组完全投入或完全退出对潜在谐振的影响,而本文不但考虑了电容器组取值变化的影响,还考虑了其他类型元件参数随机变化的影响,且本文中电容器组的取值根据负荷需要补偿的无功功率进行设定,更符合电网的实际运行情况。因此,本文考虑场景下所得的系统节点导纳矩阵无法完全包含按文献［11］方法所得的节点导纳矩阵,这便导致在少量频段处文献［11］能搜索到的谐振关键模态未能通过本文方法搜索到,但这是本文考虑了更多实际场景后的更为合理的现象。

综上,正因为本文提出的PRMM 面向图2（b）中实际存在的潜在谐振而建立,故PRMM 能够更加客观而准确地刻画各节点的潜在谐振可观性。

限于文章篇幅,下文以图2 中21～24 p.u.频带内的全部谐振关键模态为例,对2 种场景下相同频带内各节点的谐振可观情况进行对比分析。

首先,分析文献［11］场景下待研究频带内各节点的谐振关键模态可观情况。仿真结果表明,该场景下共有3 个节点具有谐振可观性,由式（12）可得这些节点的ROI 值如表1 所示；各节点可观与不可观的谐振关键模态如图3（a）和（b）所示。

表1 文献[11]场景下具有谐振可观性节点的ROI 值Table 1 ROI values of buses with resonant observability in the scenario of reference [11]

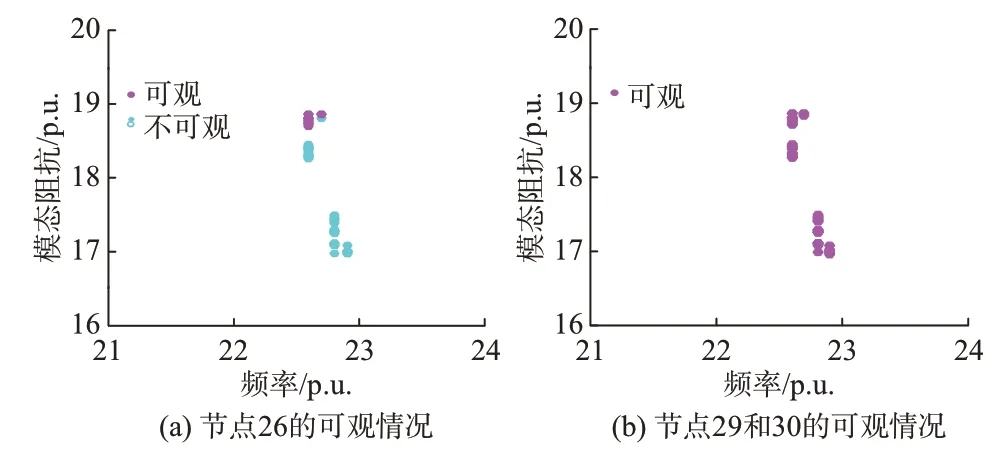
图3 文献[11]考虑场景下各节点可观与不可观的谐振关键模态分布Fig.3 Distribution of observable and unobservable resonance critical modes of each bus in the scenario of reference [11]

由表1 和图3 可以看出,当仅考虑并联电容器组完全投入或完全退出时,仅在节点29 或仅在节点30处安装监测装置均能实现该场景下的谐波谐振完全可观,即选择节点29 或30 安装监测装置是实现谐振完全可观且所需装置数最少的配置方案。

下面分析本文考虑系统参数不确定性场景下待研究频带内各谐振关键模态的可观情况。仿真结果表明,在本文场景下共有6 个节点具有谐振可观性,这些节点的谐振可观性指标如表2 所示；各节点可观与不可观的谐振关键模态如图4（a）～（f）所示。

表2 本文场景下具有谐振可观性节点的ROI 值Table 2 ROI values of bues with resonant observability in the scenario of this paper

图4 本文考虑场景下各节点可观与不可观的谐振关键模态分布Fig.4 Distribution of observable and unobservable resonance critical modes of each bus in the scenario of this paper

由表2 和图4 可以看出,对于能够实现文献［11］场景下各谐振关键模态完全可观的节点29 或30 均未能实现本文考虑场景下全部谐振现象的完全可观,被二者大量遗漏的谐振现象需通过节点3、5、26 或28 才能观测到。

综上,在仅考虑并联电容器组完全投入或完全退出场景下分析谐振现象时,将有大量潜在谐振现象被遗漏,且在相同频带内,该场景下能够实现谐振完全可观且所需装置数最少的配置方案在本文考虑的实际场景中未必能够实现谐振完全可观。充分考虑系统元件参数取值的不确定性对有效刻画各节点的潜在谐振可观性具有重要意义。

5.3 优化配置结果与分析

下文分别采用文献［11］中基于RMM 的方法和本文提出的基于PRMM 的方法对测试系统进行谐振监测点优化配置。在应用本文方法进行优化配置时将OCTF 限值βt,max设置为0,即暂不考虑谐振可观性与投资经济性之间的权衡,所得结果如表3所示。

表3 优化配置结果Table 3 Optimal placement results

首先分析在监测装置充足时,本文所提优化配置方法是否能够实现谐振的完全可观。由表3 可知,通过RMM 法所得配置方案的ROI 值为89.61%,未能实现实际情况下谐振的完全可观,原因正如5.2 节中的谐振可观性分析,即RMM 法旨在面向图2（a）中各谐振关键模态进行监测点优化配置,但能够实现对这些关键模态完全可观且装置数目最少的配置方案并不能实现图2（b）中系统实际存在的潜在谐振关键模态完全可观。而由于本文考虑了系统不同类型元件参数随机变化这一事实,直接面向系统实际存在的各谐振关键模态进行优化配置,故能获得ROI 值为100%的配置方案。

此外,相比于文献［11］中的RMM 法,采用本文方法除能够提供以最少装置数实现谐振完全可观的配置方案以外,还可以提供监测装置数目有限时实现ROI 值最大化的配置方案。例如,由表3 可知,实现ROI 值为100%至少需要11 台监测装置,但若投资方短期内仅能提供5 台监测装置,则可以选择节点3、5、18、26、29 作为最优配置方案,该方案能够达到的ROI 值为93.97%,是全部C530种配置方案对应各ROI 值中的最大者。由表3 还可以进一步看出,当监测装置数目与RMM 法所得方案装置数目相同（均为9）时,本文所得方案达到的ROI 值为99.91%,比RMM 法提高了11.49%。而当采用PRMM 法达到的ROI 值与RMM 法达到的ROI 值相近时（ROI 值为87.19%）,PRMM 法所需监测装置数仅为4 台,比RMM 法所需监测装置减少了5 台。

根据表3,图5 给出了最大ROI 值随装置数的变化曲线。可以看出,随着监测装置数目的增多,最大ROI 值αr,max逐渐增大,但增长速率却逐渐放缓。这意味着在一定范围内,更少的监测装置数目对应的αr,max可以近似于资金允许范围内能够达到的αr,max,而本文提出的OCTF 可作为量化这种近似程度的参数。

图5 不同监测装置数目对应的最大ROI 值Fig.5 The maximum ROI value corresponding to different numbers of monitoring devices

最终的优化方案由最多能提供的装置数N1和设定的OCTF 限值βt,max共同决定。假如N1为11,此时由表3 可知基准方案可恰好在监测装置全利用的情况下实现ROI 值为100%。若投资方设定的βt,max值为5%,则认为ROI 值不低于95%即可满足谐振可观性的要求。此时按照3.3 节中的方法可得到最终配置方案为表3 中装置数为6 且ROI 值为97.68%对应的配置方案。相对于基准方案,最终方案的ROI 值下降率仅为2.32%＜5%,但可减少装设5 台监测装置所需的成本。

表4 列举了几种不同的N1和βt,max取值情况下的优化配置结果。可以看出,当N1确定时,βt,max越大,在谐振可观性与投资经济性权衡过程中对可观性的要求就越低,也越容易降低投资成本。在实际工程应用中,投资方可根据自身对谐振可观性的要求,选择适当的βt,max值,从而在自身经济条件限制范围内能够达到的最大ROI 值基础上,适当放宽对谐振可观性的要求,以获得相应的成本收益。

表4 N1和βt,max取为不同值时的优化配置结果Table 4 Optimal placement results with different values of N1 and βt,max

5.4 相关参数变化对优化配置结果的影响

在优化配置过程中,判断谐振可观与否的阈值τ、建立PRMM 所需的蒙特卡洛仿真总次数以及各随机变量标准差的选择会对谐振完全可观所需的最小装置数N2带来影响。根据式（13）所示的优化模型,本节将在5.3 节算例基础上,对相关参数变化对N2值的影响规律进行分析。

5.4.1 阈值选择对配置结果的影响

表5 给出了不同阈值时以谐振完全可观为约束的优化配置结果。可以看出,随着阈值τ取值的逐渐减小,实现谐振完全可观所需的最少装置数也逐渐减少,这是因为正如式（10）所示,τ的取值越小,MPRMM,ij取值为1 的可能性越大,即各节点能够观测到的谐振关键模态比例就越大,这便导致所需较小数量监测点即可实现谐振完全可观。

表5 不同阈值时以谐振完全可观为约束的优化配置结果Table 5 Optimal placement results under the constraint of resonance complete observability with different thresholds

但需要注意的是,并联谐振监测应以系统严重的节点谐波电压放大现象来明显地提示系统当前正承受谐振干扰,尽管选择较低的阈值可以降低谐振完全可观所需的最少监测点数,但当谐振发生时,低阈值对应配置结果所选监测点处的谐波电压放大程度可能并不明显,从而易导致谐振现象被电力部门所忽视。因此,从既保证谐振监测的可靠性又保证投资经济性的角度出发,阈值τ可选择低于1 但接近于1 的数值,如上文算例中选择的阈值0.95。

5.4.2 蒙特卡洛仿真次数对配置结果的影响

表6 给出了不同蒙特卡洛仿真次数时以谐振完全可观为约束的优化配置结果。

表6 不同蒙特卡洛仿真次数时以谐振完全可观为约束的优化配置结果Table 6 Optimal placement results under the constraint of resonance complete observability with different Monte Carlo simulation times

由表6 可以看出,在蒙特卡洛仿真次数不超过3 000 次的范围内,随着仿真次数的增加,优化配置结果所需监测点数也逐渐增加,这是因为在ROI 值未收敛前,抽样次数越多越容易搜索到具有不同特征的谐振关键模态,而实现更多不同特征谐振关键模态完全可观的最少装置数也就越多。而当抽样次数超过3 000 次时,优化配置结果趋于稳定,即只需要11 台监测装置即可实现谐振完全可观,这是因为当蒙特卡洛仿真次数超过3 000 次时,不同配置方案的ROI 值已趋于收敛,因此对应于ROI 值为100%且装置数目最少的配置方案将不再改变。

5.4.3 系统参数标准差取值对配置结果的影响

如2.1 节所述,本文按各元件参数有99.7%的概率出现在区间μ±μδ内设置标准差,此时,表7 给出了不同δ值时以谐振完全可观为约束的优化配置结果。由表7 可以看出,随着δ值的逐渐降低,优化配置结果所需监测点数也逐渐降低,这是因为元件参数变化范围越小,系统具有不同特征的潜在谐振关键模态数量就越少,实现这些谐振现象完全可观的最少监测点数也就越少。

表7 不同随机变量标准差时以谐振完全可观为约束的优化配置结果Table 7 Optimal placement results under the constraint of resonance complete observability with different standard deviation of random variables

6 结语

本文提出一种并联谐波谐振监测点的优化配置方法,该方法充分考虑了电力系统不同类型元件参数取值随机变化对谐波谐振潜在性与可观性造成的影响,并能够在确保监测装置数目满足投资成本限定的前提下,实现谐波谐振可观性与投资成本经济性之间的协调优化。通过与现有方法进行对比分析可知,本文在监测点优化配置过程中面向的谐振现象更加接近于系统实际存在的谐振现象,优化配置方法更符合工程实际应用场景。主要结论如下：

1）本文所建立的PRMM 能够描述各节点对更多系统实际存在的潜在谐振现象的可观性,基于PRMM 提出的ROI 可以描述任意配置方案的谐波谐振观测能力；

2）根据投资方能够提供的最大装置数以及设定的最大OCTF 值,采用本文基于PRMM 的方法可以在任意监测装置数目限定的条件下,给出权衡谐振可观性以及投资成本经济性的最优配置方案,既克服了现有方法忽略实际工程应用中对装置数目限定的问题,又克服了现有方法未能权衡谐振可观性与投资成本经济性而导致某些情况下所得配置方案低性价比的问题。

本文研究得到国网山西省电力公司科技项目(52053018000z)的资助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。