考虑分布式电源不确定性的配电网改进仿射状态估计

曲正伟，张嘉曦，王云静，李弘文

（1. 电力电子节能与传动控制河北省重点实验室（燕山大学）,河北省秦皇岛市 066004；2. 国网冀北电力有限公司检修分公司,北京市 102488）

0 引言

配电网状态估计能够为高级配电运行的实时监视分析、控制保护、经济调度等功能提供可靠的数据支持。然而,随着高渗透率可再生分布式电源（distributed generator,DG）并网发电,DG 波动性和随机性使配电网出现功率双向流动、节点电压波动加剧等现象,进而给配电网的运行、态势感知带来挑战,威胁到配电网系统安全［1-3］。因此,在配电网状态估计过程中,需要考虑更强的不确定性和常态化的随机波动因素,并对其进行合理的建模。

当前,对配电网状态估计中的不确定性问题通过随机模型［4-5］、模糊数模型［6］和区间数模型［7-8］建模。随机模型和模糊数模型需要通过大量的历史数据获取概率密度函数或隶属度函数。而实际中,对于风电、光伏等DG 很难获得准确的先验函数,在状态估计中反而会恶化结果,而区间数模型只需每个不确定性变量的上下界,不需要特定的分布,所以更适用于工程实际［9］。

对于区间状态估计的研究主要从区间运算方法、区间优化模型［10］以及区间约束模型［11］展开。传统区间运算（interval arithmetic,IA）在运算过程中,由于忽略区间输入变量间存在的相互依赖,会使得区间进一步扩张,出现误差爆炸的现象。区间迭代的优化算法能够将区间收敛到一个较窄的范围,文献［12］利用Krawczyk 算子进行迭代,不断逼近解集外壳,但由于忽略多区间变量之间的关联性和耦合性,影响了收敛性能,导致边界结果过宽。文献［13］提出基于未知约束理论的区间优化模型,并采用线性规划方法有效求解,但基于线性化的方法不能保证最优解［14］。作为IA 方法的发展,仿射运算（affine arithmetic,AA）能够在运算过程中考虑多个变量之间的关联性和耦合性,并在迭代过程中具有较好的收敛性,已成为分析含DG 区间潮流的有效手段［15-17］。鉴于仿射及其改进运算在区间潮流中的广泛研究,其在解决具有不确定性的配电网区间状态估计中也具有很大的应用前景。文献［18］提出对不确定量进行仿射描述,并用AA 进行状态估计的求解方法,但其在运算过程中用仿射中心值进行简化和替换,使结果不能保证解的完备性,而且仿射非线性运算过程复杂,产生大量新的噪声元,造成结果较为保守,计算效率低。

微型同步相量测量单元（micro synchrophasor measurement unit,μPMU）能够满足配电网高精度的测量目标,测量各安装节点每个周期带时间戳的电压相量及相邻支路电流相量,与PMU 相比,其安装成本低,并且能分辨出低至±0.01°的角度差,更加适合配电网的运行特性［19-20］。

为此,本文提出一种配电网改进仿射状态估计方法,其在所建立的含μPMU 生成伪测点的模型基础上,通过对DG 出力区间的仿射描述,建立了仿射状态估计模型,增加了迭代过程中DG 之间的联系,收敛效果好。通过量测变换策略减少了新增噪声元从而降低运算复杂性,并通过改进的仿射运算（modified affine arithmetic,MAA）方法进行有效求解。在保证解完备性的基础上,进一步降低解的保守性,仿真结果验证了本文方法的有效性。

1 基于支路电流的状态估计

1.1 含μPMU 生成伪测点的混合量测系统

1.1.1 μPMU 量测数据

对于配置μPMU 量测的节点,其呈现的测量值为极坐标形式,利用坐标变换公式将其转化为直角坐标,如式（1）所示。

式中：V̇i,pmu和İij,pmu分 别为μPMU 所在节点i的 电压相量和支路ij的电流相量；i,j∈N,N为配电网节点集合。

1.1.2 SCADA 及AMI 量 测 数 据

数据采集和监控（supervisory control and data acquisition,SCADA）系统是传统状态估计的量测数据来源,虽然能够保证配电网状态估计的可观性,但其精度较低,仅能测量所在节点的电压和电流幅值、有功功率和无功功率。高级量测体系（advanced metering infrastructure,AMI）在用户侧测量,同样可获得节点功率和支路功率,两者的量测数据通过等效量测变换,可将其测量端点处的功率型数据经过实部虚部解耦转化成节点注入电流相量,表达式为：

式 中：İi,eq为节点i等 效 注 入电流相量；Ṡi,m=Pi,m+jQi,m为节点i的量测功率,由SCADA 和AMI 量测的节点负荷有功功率Pi,m和无功功率Qi,m组成；V̇i为节点i的电压相量；( ⋅)*表示相量实部和虚部的解耦运算。

类似地,可将SCADA 和AMI 的支路功率量测转换为等效支路电流量测。

1.2 μPMU 生成伪测点模型

在配电网状态估计中,伪量测（pseudo measurement,PSO）能够补充数据冗余度,提高网络可观性,其精度对状态估计精度有决定性的作用。在含高渗透率DG 的配电网中,受DG 大规模接入、DG 投切频繁和配电网网络拓扑多变的影响,全系统运行状态复杂度与变量维度规模化增长,机器学习方法较难适应高随机性及动态变化特性,导致其伪量测精度难以保证［21］。为了改善伪量测数据的精度,本文基于μPMU 的节点电压和支路电流的相量量测数据,通过基尔霍夫定律生成与之相邻的μPMU 伪测点数据,采用测量不确定度传播理论［22］获得其测量误差,能够从状态估计数据输入端就确保伪量测的精度,增加伪量测的可靠性［23］。

测量不确定度传播理论是指间接观测量的值通过运算模型由直接观测量获得,但因直接观测量中带有一定误差,所以间接观测量的误差由直接观测量的误差传播而产生,设Z是n个独立观测量t1,t2,…,tn的函数,即

式中：t1,t2,…,tn为直接观测量,相应的观测误差分别为m1,m2,…,mn,则间接观测函数Z的误差如式（4）所示。

式中：m(tk)为观测量tk的标准偏差。

具体的μPMU 配置点网络可观情形如附录A图A1 所示,为保证伪量测精度,伪测点数据的生成模型仅考虑与μPMU 直接相关联的点而不再进行二次扩展,即μPMU 伪测点的另一端所连节点不再可观,达到补充高精度数据冗余的效果。考虑到安装经济性,根据附录A 图A2 所示的配电网π 型结构图,通常采用附录A 式（A1）作为伪测点生成模型,并生成节点i的电压伪量测量V̇i,pso。

1.3 DG 注入功率

目前,在配电网稳定分析过程中,常规负荷及DG 大多采用PQ控制方式,即根据给定的功率因数计算出光伏出力和风机出力的无功功率。当以某一个时间断面分析配电网运行状态时,DG 出力往往是以确定的有功功率和无功功率的形式注入所在节点。通过等效量测变换,将其功率型数据经过实部虚部解耦转化成节点注入电流相量,即

式 中：İi,DG为 节 点i等 效 的DG 注 入 电 流 相 量；Ṡi,DG=Pi,DG+jQi,DG为 节 点i的DG 功 率,由DG 出力的有功功率Pi,DG和无功功率Qi,DG组成。

所有量测数据经过上述量测变换的处理,转换成直角坐标形式的电流相量,实现了量测形式的统一,则量测数据构成为基于电压和电流的混合量测系统ZM,表达式为：

1.4 算法原理

支路电流法基于加权最小二乘法,根据电压、电流之间的线性关系,以支路电流İij的实部和虚部为状态变量进行状态估计,状态量表示为：

式中：x为n维状态向量。

配电网的量测模型可以表示为：

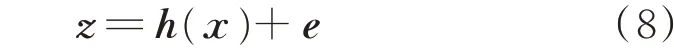
式 中：z=[z1,z2,…,zm]T为m维 量 测 向 量；h(⋅)为量测函数；e为量测误差向量,服从均值为零的正态分布。

支路电流法是加权最小二乘法的衍生,其最小化目标函数为：

式中：w=R−1为量测权重矩阵,R为n个量测误差组成的协方差矩阵；c(⋅)为对系统中存在的零注入功率添加等式约束条件,对状态估计结果加以修正,进而提高状态估计精度。

2 仿射运算

2.1 仿射及其运算

AA 通过引入噪声元来增加不确定变量之间的相关性,解决IA 中的区间扩张问题［24］。一个不确定区间变量u可表示为一组具有噪声元的仿射线性组合,即为仿射数：

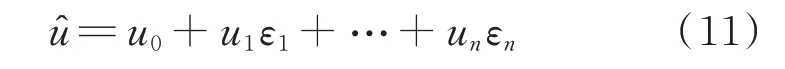
式 中：u0为 中 心 值；噪 声 元εi∈[−1,1],i=1,2,…,n为不确定性因素；ui为噪声元系数,表示不确定性因素对变量u的影响程度。

仿射线性运算不会产生新增噪声元,而在乘法和除法等非线性运算过程中,通常以新增的噪声元来代替运算产生的噪声元二次项,或者采用某种近似法则来逼近其真实解［25］,对于给定的2 个仿射数û和v̂,AA 的乘法如式（14）所示。

式中：a和b分别代表仿射数v̂的区间上、下限；α1、β1和δ为参数。

复仿射数除法运算与实仿射类似,可被分解为仿射的乘法、平方以及倒数运算,有

如式（16）所示,2 个复仿射数除法运算将会产生5 个新增噪声元,新增噪声元过多将会导致运算复杂且会影响仿射运算结果的保守性。所以,仿射的非线性运算是导致仿射区间扩张的原因。

2.2 改进的仿射运算

不论是IA 还是AA,其结果一般采用2 种标准来评价：一是解的完备性,即运算结果能否包含真实解的所有范围；二是保守性,即运算结果在保证解完备性的基础上,对真实解变化范围的接近程度,运算结果过于保守将失去工程价值。AA 能够保证解的完备性,但是由于仿射非线性运算过程中会产生大量新的噪声元,不可避免地会使解过于保守。

对于仿射乘法运算,式（14）中等号右边前2 项是已有噪声元的仿射形式,第3 项是用新增噪声元来代替仿射噪声元相乘产生的二次项。因此,改进方法的主要目的是对最后一项新增噪声元及其系数找到一种新的仿射近似方法。

针对新增噪声元导致的区间扩张问题,本文采用MAA,通过合并新增的相同噪声元项并对其系数进行求和逼近,减少解的保守性［26］,实数域的MAA 表达式为：

首先,在MAA 中,保留了AA 式（14）中等号右边的前2 项。其次,式（14）中等号右边的最后一项的近似值返回结果为绝对值,则有uiviεk∈[0,uivi]。然后,相较于AA 将各噪声元系数乘积的绝对值和直接近似,此MAA 将具有相同噪声符号εiεj的项合并,通过对其系数|uivj+ujvi|求和来逼近。这样的改进方式减少了由近似项带来的区间扩张问题,避免了结果的保守性,而且其绝对值总和也保证了解的完整性,确保解的完备性。

在复仿射 域 中,2 个复仿射 数ûc和v̂c的MAA 乘法运算为：

式中：zreal和zimag分别为新增实部和虚部噪声元的系数；εreal和εimag分别为新增实部和虚部的噪声元。

IA、AA 和MAA 在运算结果的完备性、保守性方面的表现在附录B 进行验证。通过验证表明,MAA 能够充分考虑变量之间的关联性,更接近并包含真实区间。仿射数建模及MAA 将用于具有不确定性的配电网仿射状态估计的迭代求解过程,将在下一章进行说明。

3 配电网区间状态估计的仿射解法

3.1 混合量测系统的仿射建模

为了对不确定性的DG 出力有更好的描述,同时能在配电网状态估计中体现其影响,本文将节点i的DG 出力在某一时间断面形成的波动性区间[Si,DG]=[Pi,DG]+j[Qi,DG]按式（12）转化成仿射数形式：

式 中：Ŝi,m和Ŝij,m分 别 为SCADA 和AMI 节 点 功 率和支路功率的仿射形式；V̂i,pmu和Îij,pmu分别为μPMU及其生成伪测点的节点电压相量和支路电流相量的仿射形式；Ṡi,0,m和Ṡij,0,m分别为节点和支路的测量仿射中心值；Pi,m和Qi,m分别为节点功率仿射形式的有功和无功功率；Pij,m和Qij,m分别为支路功率仿射形 式 的 有 功 和 无 功 功 率；V̇i,0,pmu和İij,0,pmu分 别 为μPMU 及其生成伪测点的节点电压相量和支路电流相量的测量仿射中心值；Vi,r,pmu和Vi,x,pmu分别为μPMU 及其生成伪测点的节点电压相量实部和虚部；Iij,r,pmu和Iij,x,pmu分别为μPMU 及其生成伪测点的节点电流相量实部和虚部；εi,P,m、εi,Q,m、εij,P,m、εij,Q,m、εi,r,pmu、εi,x,pmu、εij,r,pmu和εij,x,pmu为各量测量的噪声元。

3.2 仿射量测变换策略

对于1.1.2 节中,SCADA 和AMI 的节点及支路功率量测、DG 的注入功率量测在状态估计过程中的量测变换过程,以DG 注入功率的量测变换式（5）为例,由于要进行复仿射数除法运算,由式（16）可知,若给定2 个复仿射功率含m个噪声元,迭代g次后,每个电流复仿射中含有噪声元数量N为：

由式（21）知,复仿射的除法计算过程由于要保证解的完备性,会产生大量的新噪声元,在迭代过程中造成量测函数矩阵的变大,运算过程复杂,耗时较长,难以收敛［27］。所以在量测变换和状态估计过程中,应尽量避免仿射数除法的运算。因此,根据配电网的运行特性,考虑实际系统中沿配电线路的小压降和正常电压极限（0.95 p.u.～1.05 p.u.）,提出适用于配电网运行特性的仿射量测变换策略,定义节点电压ΔVk=1−Vk,Vk为参数,在0 附近采用泰勒级数展开［28］,即

图1 泰勒级数近似度评估图Fig.1 Taylor series approximation evaluation

利用仿射形式的泰勒级数展开近似,式（5）可表示为：

式中：(Îi,DG)*表示节点i等效的DG 注入电流仿射数形式；V̂i为节点i电压相量的仿射数形式。

同理,可将节点和支路注入功率的量测变换过程利用仿射量测变换策略进行转换。

仿射量测变换后得到乘法量测变换运算过程,由式（25）可知,由给定的具有m个噪声元的复仿射功率,进行g次迭代后,每个电流复仿射中含有噪声元数量N为：

相较于式（21）,新增噪声元数量显著减少。

3.3 配电网仿射状态估计

配电网仿射状态估计步骤如下。

步骤1：输入网络参数,获取量测值以及DG 出力的波动性区间；将量测值和DG 波动性区间按照式（19）和式（20）变换成仿射数的形式。

步骤2：利用式（24）仿射量测变换策略进行量测变换,将仿射除法用仿射乘法替代,减少非线性运算新增噪声元。

步骤3：根据状态量以及仿射运算规则,构造仿射量测函数并计算雅可比矩阵。

步骤4：迭代求解,求取状态估计中修正量的仿射表达式,进而求出状态变量的仿射形式。

步骤5：将第k次迭代的状态量转化成区间形式,并将其实部与虚部的上下限分别与k-1 次迭代结果作差,满足收敛条件后输出区间形式的状态变量,若不满足,则进行迭代计算,直到满足则输出区间结果,收敛条件为：

4 算例仿真

4.1 含μPMU 生成伪测点的状态估计

采用IEEE 33 节点典型配电网单相测试系统进行仿真验证,系统拓扑、DG 及量测配置如附录C图C1 所示。网络首端基准电压为12.66 kV,基准容量为10 MVA,节点1 为平衡节点,系统存在2 个零注入点 ,除 去 零 注 入 点 后 系 统 的 总 负荷 为（4 964.26+j2 507.32）kVA。仿真系统真值由潮流计算得到,量测数据在系统潮流计算的结果基础上添加相对应的满足正态分布的随机误差形成。

在系统中的节点9 接入光伏机组,功率为（284.7+j93.576）kVA,节点23 接入光伏机组,功率为（268.4+j88.219）kVA,节点29 接入风电机组,功率为（194.6+j63.962）kVA。μPMU 幅值和相角量测的标准差分别为0.002 和0.005,SCADA 系统功率测量标准差为0.02,AMI 量测数据标准差为0.01,μPMU 生成伪测点的测量标准差由测量不确定度传播生成。本文忽略量测装置采样周期不同,量测值均假设为同一时间断面采集数据,收敛精度取10−4并采用3 种方案进行验证。

方案1：除了DG 节点,SCADA 覆盖整个系统,终端负荷配有AMI 量测。

方案2：在方案1 的量测配置基础上,根据μPMU 装置的优化布点,综合权衡投资和状态估计精度,可在节点15、19 和28 配置μPMU［29］,形成混合量测模型。

方案3：在方案2 的量测配置基础上,添加μPMU 生成伪测点,提高量测冗余度,进行状态估计仿真验证。

由图2 所示3 种方案的电压幅值和相角的估计误差结果可以看出,方案2 和方案3 的状态估计误差均小于方案1。从整个系统来看,当系统安装有限个μPMU 并根据测量误差传播形成的伪量测能够提高量测的冗余度,并且由于μPMU 的量测精度远大于其他量测设备,生成的伪量测精度高。所以,方案3 的状态估计精度又有所提升,验证了含μPMU 生成伪测点的基于支路电流状态估计方法的有效性。

图2 不同方案的误差对比图Fig.2 Error comparison of different schemes

4.2 配电网改进仿射状态估计

4.2.1 IEEE 33 节点系统

为研究本文改进仿射状态估计的估计效果,在上述方案3 的基础上,取一个时间断面的DG 出力区间作为节点功率注入,功率因数为0.95,具体波动区间如附录C 表C1 所示。将2 个光伏分别接入节点9和23,将风电接入节点29。SCADA 和AMI 的量测值为潮流真值基础上添加噪声p=0.5,μPMU 添加p=0.05 形成仿射区间,在此基础上,分别按照本文的MAA 方法、基于集合逆变换的非线性区间分析（set inverter via interval analysis,SIVIA）方 法［30］以及Monte Carlo 方法进行区间状态估计分析,其结果如图3 所示。

图3 区间状态估计结果Fig.3 Results of interval state estimation

如图3 所示,通过3 种求解方法形成的区间状态估计结果的对比分析可得,DG 的波动会给系统节点电压幅值和相角带来一定范围内的波动。以Monte Carlo 方法模拟5 000 次获得的状态量波动区间来反映DG 出力不确定性造成系统状态量变化的真实范围,基于SIVIA 方法的状态估计结果能够包含系统状态量的真实范围,保证了解的完备性,但相较本文基于MAA 方法的状态量区间结果,其结果相对保守。这是由于SIVIA 方法在求解过程中需要不断地对区间进行二分,容易导致区间扩张,而本文MAA 方法通过噪声元建立不确定变量之间的依赖关系,在量测变换和乘法运算过程中减少噪声元的产生,降低运算复杂程度,缓解了保守性。所以基于MAA 方法的状态估计解的结果更接近Monte Carlo 方法的区间结果,对比SIVIA 方法保守性更低,说明本文考虑DG 出力不确定性采用的改进仿射状态估计方法的有效性。

为对上述3 种方法求解结果在保守性方面进行更为直观的对比,在上述分析基础之上对状态估计结果的区间宽度进行对比分析,采用2 项指标对保守性进行评估［8］,α为节点电压幅值或相角的平均区间宽度,β为节点电压幅值或相角的最大区间宽度,xˉi和-x i分别为量测值的最大和最小值,表达式为：

附录C 表C2 给出了3 种方法的区间结果宽度指标,能更直观地得出3 种方法的保守性对比,本文采用的仿射区间状态估计方法的区间宽度要比SIVIA 非线性区间求解方法的窄,而且更接近于Monte Carlo 方法的真实状态量变化区间。因此,保守性更低,状态估计结果更可靠。

为了测试本文所提方法在不同波动程度的DG出力中的性能,在上述DG 出力区间基础上,分别添加±5%、±10%和±20%的波动,形成新的DG 出力区间,其状态估计结果的平均区间宽度和最大区间宽度如表1 所示。

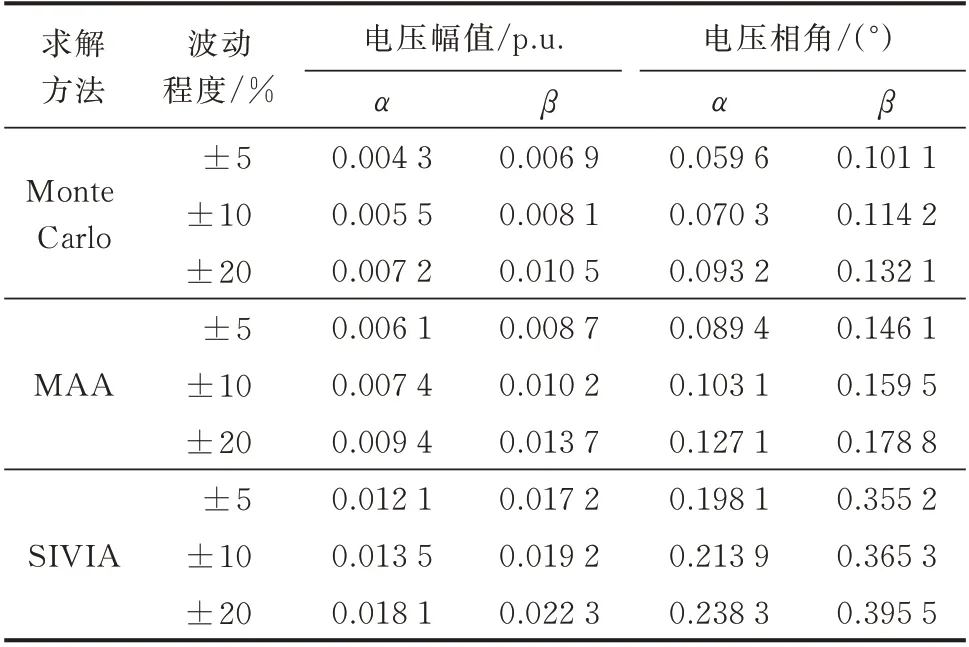
表1 不同方法在DG 波动程度中的性能对比Table 1 Performance comparison of different algorithms with DG uncertainty

由表1 可以看出,DG 出力波动程度不同扩大了状态估计结果的变化区间,而且波动程度越大,状态估计结果的区间宽度越宽,但本文所提MAA 方法能够始终接近于Monte Carlo 方法真实解集的区间变化结果,具有理想的估计性能。

4.2.2 IEEE 118 节点系统

采用大规模IEEE 118［31］辐射型配电网测试系统验证本文所提方法的有效性,并增强DG 渗透程度,拓扑结构见附录D 图D1,DG 接入位置见附录D表D1,在全网配有SCADA 量测的基础上,增加μPMU 量测,μPMU 伪测点根据1.2 节生成,仍采用MAA 方 法、SIVIA 方 法 和Monte Carlo 方 法 进 行 区间状态估计分析,状态估计结果如图4 所示。

由图4 可以看出,虽然受高渗透率DG 波动性影响,大量节点的状态量变化范围较大,但相较SIVIA方法,本文所提MAA 方法的状态估计结果能够更接近真实值。因此,在含DG 波动的大规模系统中,本文方法仍有较强的实用性。

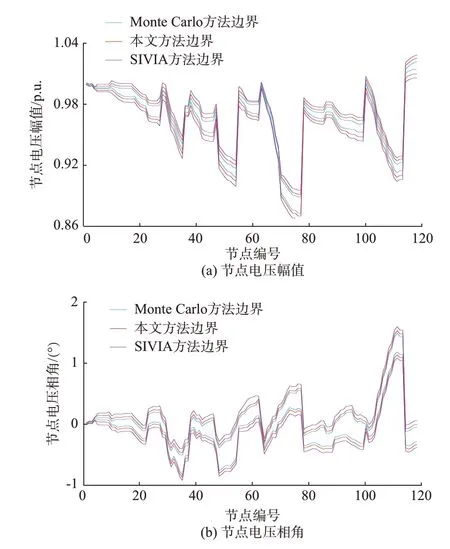
图4 节点电压幅值和相角的区间状态估计结果Fig.4 Interval state estimation results of bus voltage amplitude and phase angle

4.3 估计效率

附录D 表D2 给出了在相同的测试环境和测试系统中3 种估计方法的计算效率对比分析结果,其结果显示本文所提MAA 方法能够以较少的迭代次数达到最佳估计值,所耗时间较短,对比非线性区间分析的SIVIA 方法,本文方法估计效率高,而Monte Carlo 方法由于单次抽样并设定5 000 次运算,其耗费时间长而失去实际价值。

5 结语

本文建立了含μPMU 生成伪测点的基于支路电流的状态估计模型,增加了网络可观性,利用测量不确定度传播理论得到μPMU 生成伪测点的测量误差,从数据输入端保证了伪量测的精度,从而直接提高配电网状态估计的精度。

在上述模型的基础上,考虑DG 出力不确定性建立了仿射状态估计模型,通过适用于配电网的仿射量测变换策略减少运算过程中的新增噪声元,降低运算复杂性,结果表明在保证完备解的基础上,降低了结果的保守性,所得状态量的区间结果更接近真实解,更具有工程价值。

本文所提的改进仿射状态估计方法能适应配电网中各种能获得上下界信息的不确定性因素,改进的仿射运算法同样适用于具有不确定性因素的潮流计算等。而在本文中,仿射状态估计所处理的网络节点类型以PQ节点为主,更加复杂的网络接口类型的仿射模型还未深入研究。此外,在实际配电工程中（尤其是城镇低压配电网）线路及负荷的三相不平衡耦合特性的场景较为普遍,还需要进一步研究三相不平衡场景中仿射算法的应用。因此,如何结合工程实际情况,对不同网络节点类型进行仿射建模和求解,实现对三相不平衡场景的应用是未来研究的方向。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。