锰矿预热窑内气固换热的数值模拟
2021-12-10荣文杰李宝宽穆永鸿
丁 宁,荣文杰,李宝宽,穆永鸿
(1.东北大学 冶金学院,沈阳 110819;2.大连华锐重工集团工程技术设计院,辽宁 大连 116000)
锰是影响钢铁产业发展的重要资源,在国民经济的发展中有不可替代的作用.锰在钢铁产业中的使用量超过了90%,是炼钢过程中重要的脱氧剂和脱硫剂;同时,锰的化学物理性质在有色金属、玻璃和电池等行业中发挥着独特的作用.锰在自然界内分布广泛,在多种岩石、矿石中都有分布,最常见的锰矿石为氧化锰和碳酸锰[1].
我国锰合金年产量约为1200万t,每吨锰合金平均冶炼电耗为4000 kW·h,属于高耗能产业.降低锰合金冶炼电耗是亟需解决的问题,常用的方法一般有提高入炉锰矿品位、提高入炉熟料比、配加硅铁冶炼渣,以及窑顶预热[2].窑顶预热可以干燥物料中的水分,同时利用电炉煤气中的热量,节能效果明显[3].
炉顶预热窑内的预热过程在机理上主要是高温烟气和固体颗粒间的对流换热,同时也存在固体颗粒间的导热及热辐射.近年来,国内外学者针对预热机理进行了许多相关研究.朱玲利等[4]计算了预热窑内高温烟气和固体颗粒之间对流换热过程的几个重要参数,得到了更适用于颗粒状固体的努塞尔数表达式.杨剑等[5]利用实验分析了强制对流换热系数,得到了多孔介质内不同堆积方式对压降及换热效率的影响,并给出了不同情况下的对流换热系数实验关联式.Tian和Arink等[6-7]以多孔介质模型为基础,考虑了达西流动和局部热非平衡效应的影响,建立了流体固体的具有黏性耗散的强制对流换热模型.数值模拟方法在预热窑方面的应用也在不断发展.廖志明等[8]以回转窑竖式预热窑为研究对象,对其温度场及流场进行了仿真分析.结果表明:相对于其他参数,对流换热系数是影响颗粒温度的决定性因素.为了降低填充床的压降从而提高整体的换热性能,池中源等[9]利用数值模拟软件对预热窑内的物料进行了二位仿真分析,结合用户自定义函数建立了多孔介质内的能量双方程,研究得到了多种参数对预热过程的影响.Bluhm-Drenhaus和Xiao等[10-11]利用CFD与DEM耦合的方法对固体颗粒和气体在窑内的温度分布进行了模拟,并分析了颗粒在窑内的下落轨迹与堆积方式以及烟气在颗粒空隙的流动过程.本文的研究对象为某公司设计的炉顶预热窑,该窑的进气结构复杂,现有的研究无法为其提供理论基础从而指导工业生产.预热窑内气体和固体的温度分布以及气体流动状态等尚不清楚,实际生产中预热窑的进气量、窑内温度分布以及出料温度等都缺少理论支撑,影响了生产中预热窑各参数的选择.
为了直观且高效地研究预热窑内气体流动状态、固体物料的预热情况以及窑内的气固温度分布从而指导实际生产,本文建立了预热窑的工业尺度计算模型,采用数值模拟的方法,利用Realizable k-ε模型和多孔介质模型来模拟分析预热窑内的流场和温度场,为生产中某些参数的确定以及预热窑结构的设计提供理论基础.
1 预热窑的结构及工作原理
预热窑的主要结构包括进气梁、出气梁以及窑体,结构示意图如图1所示,进气梁和出气梁的尺寸见表1.预热窑包含进气梁4根(2根整梁和2根半梁)及出气梁3根(1根整梁和2根半梁).每根进气梁上有45个进气孔,每根出气梁上有40个出气孔.该预热窑的工作原理是:高温烟气进入4根进气梁内,然后通过进气孔进入窑内,高温烟气向上运动并通过出气孔进入出气梁,从而排出窑外;同时固体物料从窑顶部进入窑内并缓慢向下运动,在窑底部出预热窑然后进入到矿热炉中,运动过程中进行能量交换.
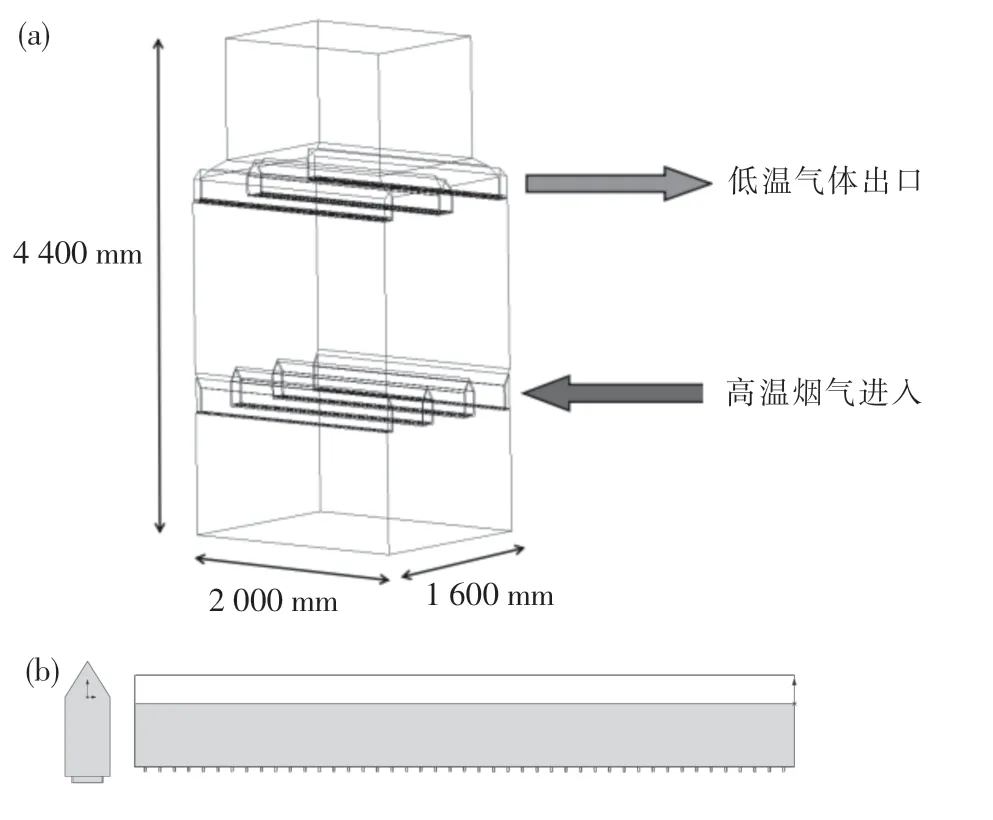
图1 预热窑和进气梁结构图Fig.1 Schematic diagram of the preheat kiln and intake beam

表1 进气梁和出气梁尺寸(长×宽×高)Table 1 The size of the intake beam and venting beam(length×width×height) mm
2 预热窑的数学模型
本文按照预热窑的实际尺寸建立了三维几何模型.但进气梁上的气孔宽度仅6 mm,该位置结构化网格的尺寸最大为3 mm,整个预热窑网格的尺寸受此限制会导致网格数过多,严重影响计算速度.因此将进气梁和窑体单独画网格,窑体关于平面对称,画网格时取半个窑.先计算进气梁内的流场和压力场,得到落料堆积角斜面上的速度分布,然后把速度通过用户自定义函数(user defined function,UDF)加到窑体堆积角斜面上再进行后续计算,从而降低窑体的网格数,提高计算速度.利用Mesh软件绘制网格,经过网格无关性验证,确定网格数为130万,网格如图2所示.
由图2可知,在进气梁下方多了一部分区域,该区域的高度和预热窑的气体入口到气体出口之间的距离相等.在计算进气梁流场时设置该部分为多孔介质区域,这样可以更准确地计算气体流过物料时的压降,得到更真实的进气梁内的气体速度.
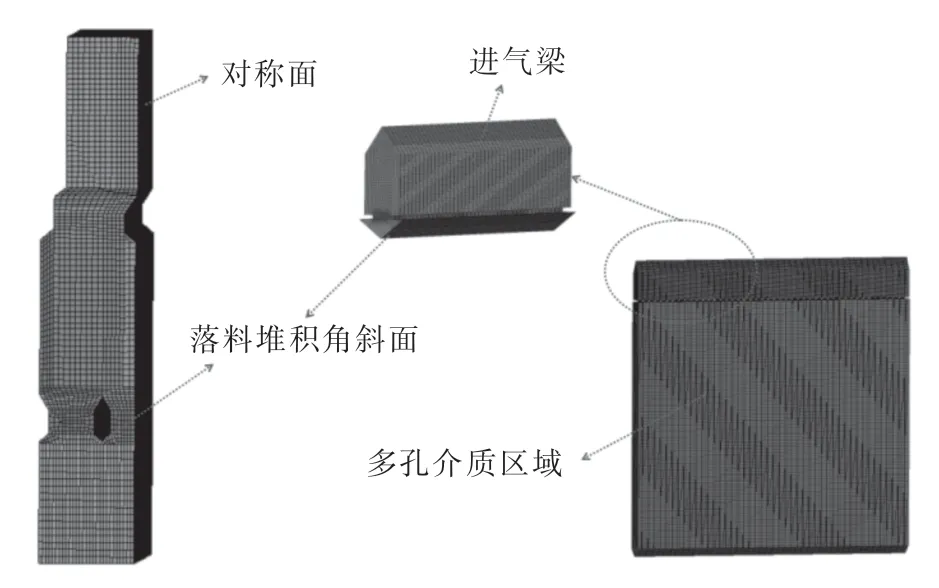
图2 进气梁及半窑网格图Fig.2 Intake beam and half kiln mesh
本文在计算时做出如下假设:多孔介质看作各相同性的均匀介质;固体颗粒均匀;不考虑边壁效应;同一水平高度的空隙率相等,空隙率在竖直方向也相等.
2.1 控制方程
连续性方程:
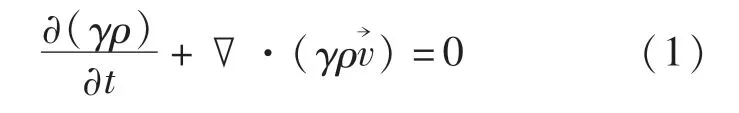
动量方程:
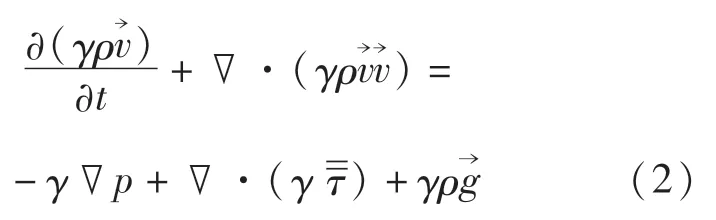
在湍流流动中,多孔介质内存在惯性阻力与黏性阻力.本文采用半经验Ergun公式计算两个阻力系数.
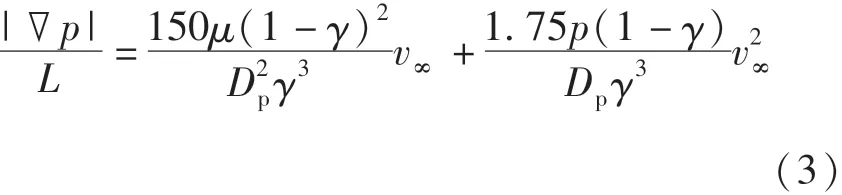
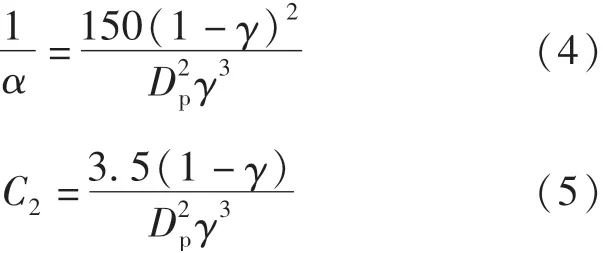
式(1) ~(5)中,ρ为流体的密度,kg/m3;P为流体的压力,Pa;→v为流体速度,为流体的黏性应力张量;为重力加速度,m/s2;μ为流体黏度,Pa·s;L为填充床的厚度,m;Dp为填充颗粒的直径,m;γ为空隙率.在本计算中,Dp为0.03 m,γ为0.39,由 式(4)(5)可 计 算 得 出1 045 477.64,C2=1 199.72.
在预热窑中物料被烟气加热,烟气与物料之间存在温差且会发生较强的对流换热[12].为了更准确地计算并且表示烟气和物料的温度分布,本文采用双温模型,烟气和物料的能量方程如下:
气体能量守恒方程:
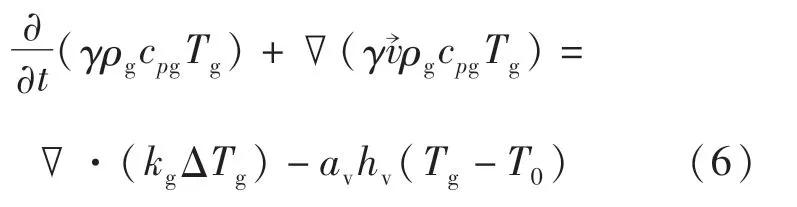
式中,ρg为气体密度,kg/m3;cpg为气体的比定压热容,J/(kg· K);av为固体颗粒的比表面积,m2/g;hv为气固对流换热系数,W/(m2·K);Tg,T0分别为气体温度和固体温度,K.公式右侧第二项表示气体与固体的对流换热.
固体能量守恒方程:
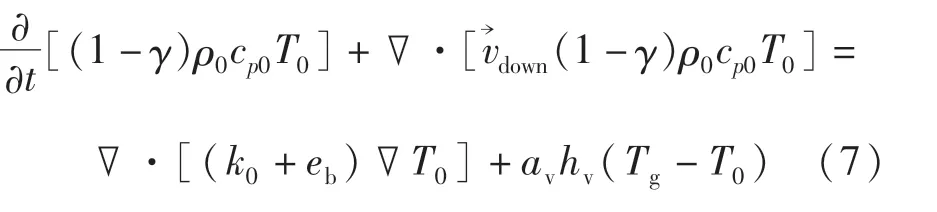
式中,ρ0为固体密度,kg/m3;cp0为固体的比定压热容,J/(kg·K);为物料下落速度,m/s.等式左边的第二项是固体温度向下的对流项,表示固体物料缓慢向下移动.等式右边第一项是多孔介质中物料颗粒间的导热与辐射之和,第二项是固体颗粒与气体的对流换热.固体颗粒间的辐射采用多孔介质的辐射等效导热系数处理[13]:

式中,σ 为斯蒂芬-玻尔兹曼常数,其值为5.6697×10-8W/(K4·m2);β为多孔介质的辐射收敛系数.
为了在多孔介质中应用双温模型,利用Fluent软件中的用户自定义标量(user defined scalar,UDS)加入固体的能量方程,并通过UDF修改气体、固体能量方程的相应项[13].
2.2 边界条件及计算方法
预热窑内气体和固体的各参数均按照实际情况给出.进气梁的入口设置为质量流量入口,吹入的气体为N2,CO2和H2O的混合气体,质量分数分别为66.1%,32.56%和1.34%,吹入气体的风量为8 505 m3/h,温度为973 K.预热窑的出口为压力出口,吸出气体成分不变,压力为-2 kPa,温度为573 K.预热窑壁面设置为绝热壁面,窑内固体颗粒以固定速度向下移动.按照最小网格尺寸和流体最大速度的关系,选取时间步长为0.045 s.在计算速度与压力的耦合问题时,选用压力耦合方程的SIMPLE算法;湍流方程中的k方程和ε方程都采用一阶迎风差分格式进行求解,其余方程皆采用二阶迎风差分处理;各方程的收敛因子均设定为10-6.
3 计算结果及分析
3.1 模型验证
采用刘颖[15]的某蓄热烧嘴实验数据对本文数学模型进行验证,建立相应的几何模型并画网格,如图3所示.该烧嘴的工作过程如下:高温烟气首先进入烧嘴对小球加热,然后通入较低温度的空气,此时小球放热,共进行两次气固换热.表2为文献[15]实验中所用的5组工况参数,运用气固换热数学模型进行计算,比较实验数据与计算结果,如表3所示.由此得出:本模型计算得到的空气出口温度和实验测量值吻合良好,相对误差最大为4.25%,验证了数学模型的可靠性.
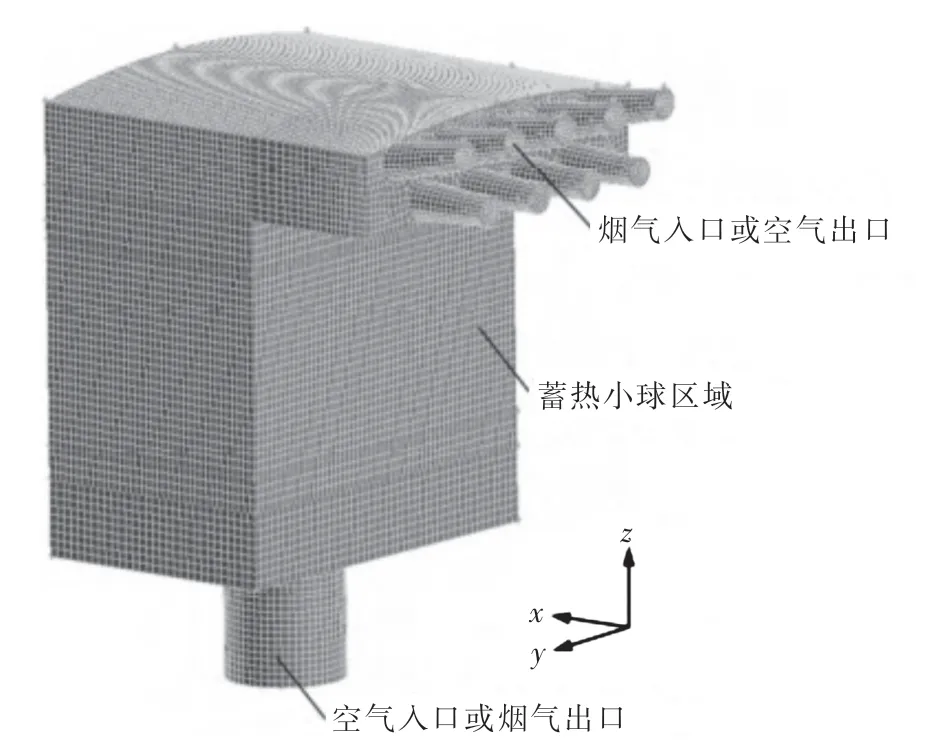
图3 蓄热烧嘴网格图Fig.3 Grid diagram of regenerative burner
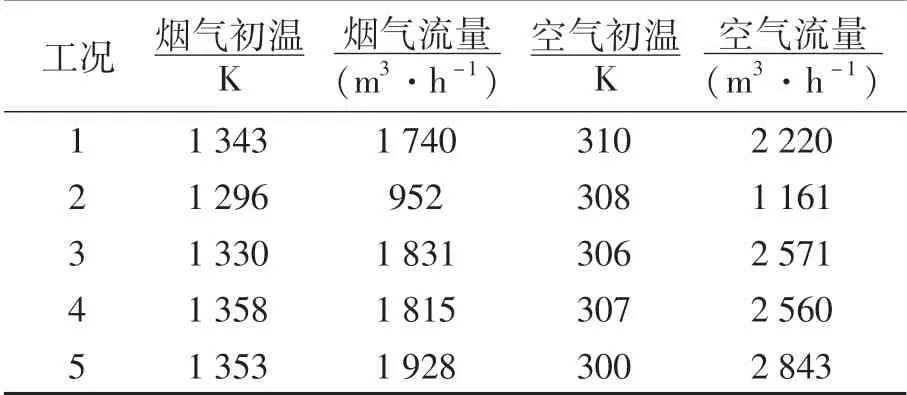
表2 测试工况参数[15]Table 2 Test parameters under different conditions
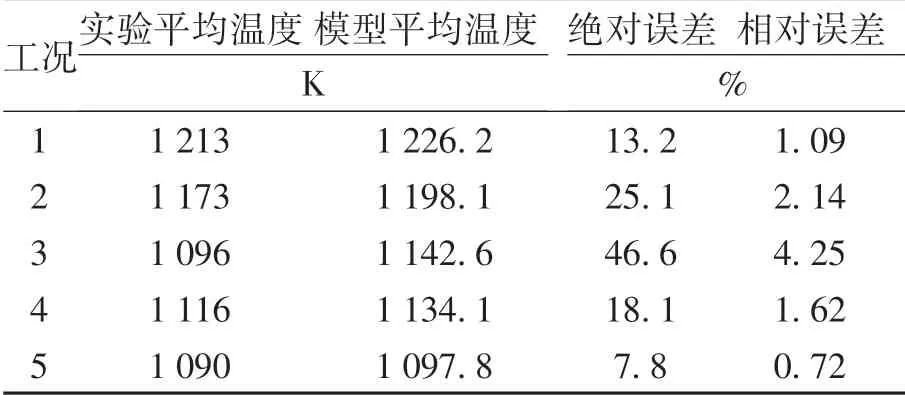
表3 蓄热体空气出口温度测量值与计算结果对比Table 3 Comparison between test data and numerical results of air preheating temperature
3.2 进气梁内烟气的流场分析
进气梁内的气体速度如图4所示,气体从梁的左侧进入并从下方的气孔流出,由于上侧和右侧封闭,在其纵截面会出现速度坡度且在右上方空间存在低速区,导致该区域内存在逆时针方向的涡流.气体通过气孔后速度最大为45.27 m/s,与企业实测速度44.6 m/s相差1.51%.

图4 进气梁的速度渲染图Fig.4 Velocity rendering of the intake beam
堆积角与窑体交界面处的速度图如图5所示,气体经过进气梁的气孔吹到该位置时速度存在最大值12.58 m/s,以最大值为中心向周围速度逐渐变小;速度主要集中在椭圆形区域内,超出该区域速度很小低于1 m/s.根据图5的速度分布图编写速度随位置变化的UDF,并将此UDF作为速度入口加载到窑体网格的堆积角斜面,进行后续计算.
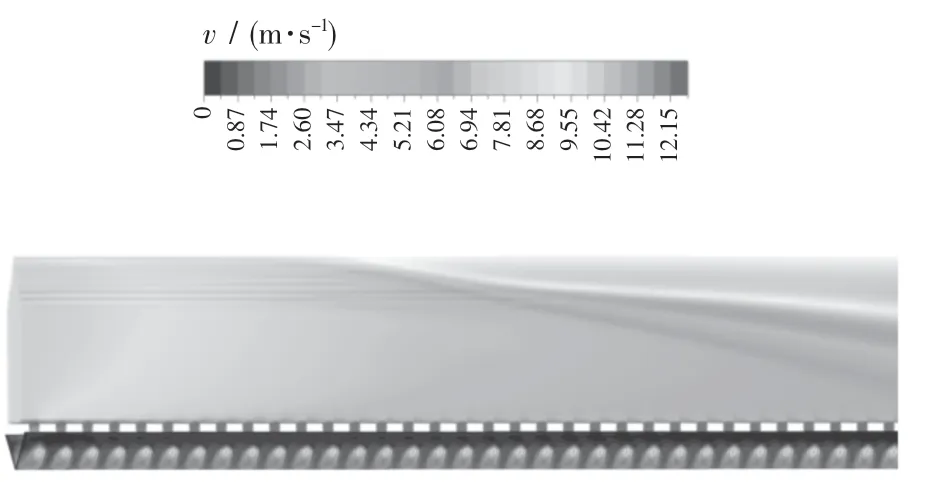
图5 堆积角斜面的速度图Fig.5 Velocity diagram of piled angular section
3.3 窑内温度场分析
根据上述条件和设置,利用Fluent对预热窑内气固换热情况及温度分布进行仿真分析.按照实际生产需求,模拟时长为1 h.预热窑内不同时刻的气体温度分布图如图6所示,3个温度图的对应时刻分别为15,30,60 min.
从图6中可以看出,气体在入口附近形成近椭圆形的高温区域.这是因为窑内堆满物料,气体进入窑内后受到物料的阻力而无法沿初始方向继续移动,会从物料的空隙中随机向各个方向扩散,从而形成椭圆形的高温区域.随着物料向下移动,气体在向上运动的过程中会受到更大的阻力,因此进气口下方的气体温度比上方的温度高.气体在出口附近的温度低于400 K,说明气固换热比较充分,气体的热量利用率高.
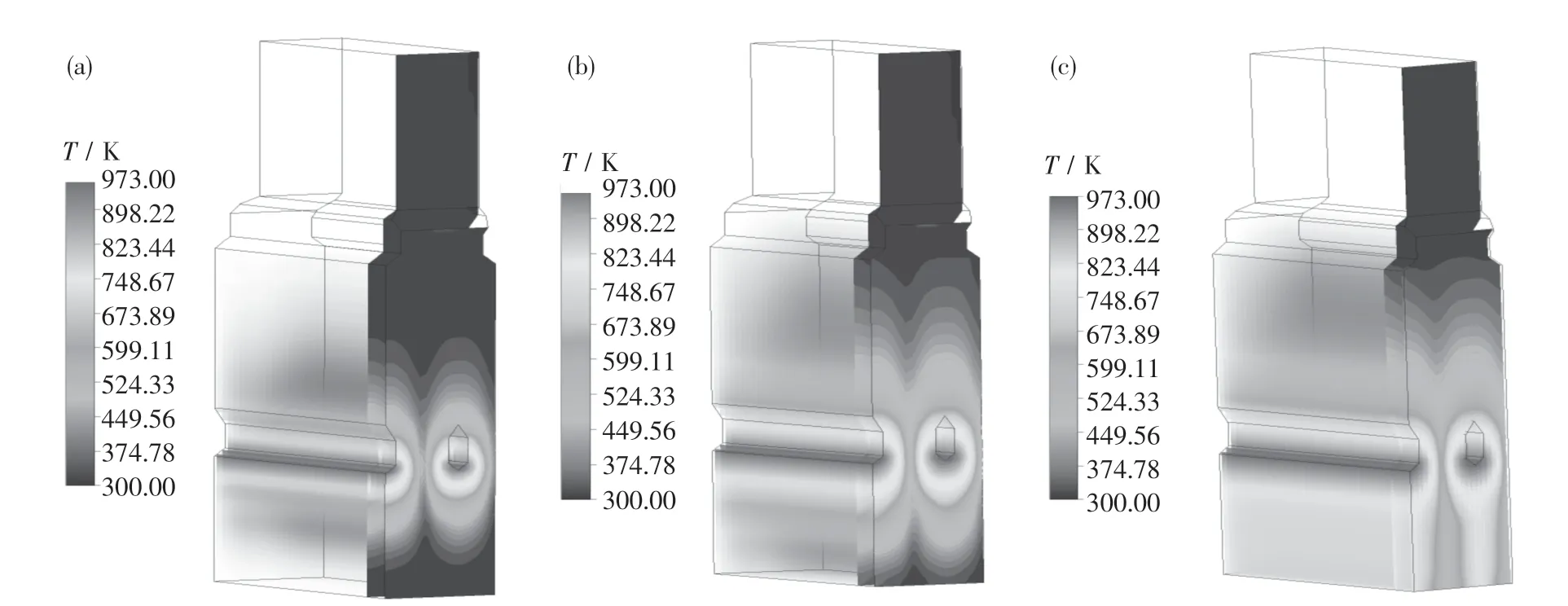
图6 15,30,60 min窑内气体温度分布图Fig.6 Gas temperature distribution in the kiln at 15,30,60 min
图7为15,30和60 min时刻的固体温度分布图.从图中可以看出:固体的最高温度分别为585.13,697.09和765.08 K;在气体入口下方存在2个柱状高温(温度高于713.38 K)区域,高温区域之间的位置温度约为550.15 K.这说明高温气体在水平方向也具有穿透性,不在气体入口下方的物料也能得到预热,窑内没有无法预热的冷区域.
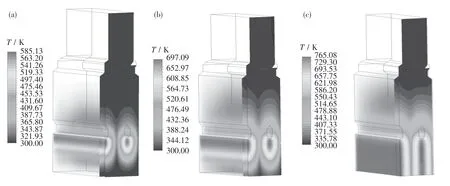
图7 15,30,60 min窑内固体温度分布图Fig.7 Solid temperature distribution in the kiln at 15,30,60 min
为了更直观地分析竖直方向和水平方向的固体温度分布情况,本文在窑内取三条线段如图8所示.线段A在两根进气梁的中间,线段B经过进气梁的纵对称面,线段C在窑底部出料口,并做出线段上不同时刻的固体温度曲线如图9所示.
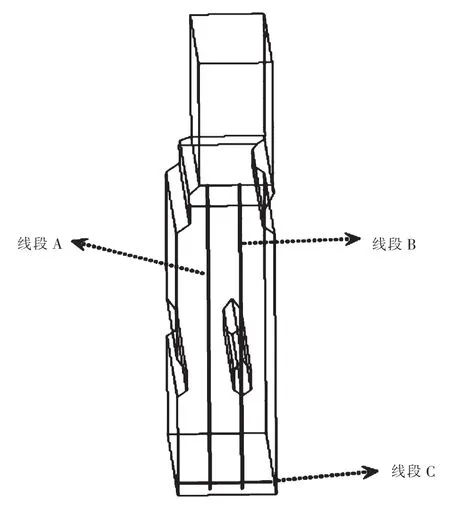
图8 三条线段的位置图Fig.8 Location map of three line segments
从图9(a)(b)得出,15,30,45 min的温度均先升高后降低,这是因为预热时间不充足,窑底部附近的物料温度低于进气梁附近物料的温度.预热60 min时,窑底部物料的温度和进气梁附近物料的温度相近.由图9(c)可以看出,4条曲线均存在2个高温点2个低温点.高温点对应进气梁正下方的物料温度最高,低温点是2根进气梁中间的物料,属于预热的低温区.预热60 min时,窑底部出口的物料最高温度和最低温度分别为762.29,524.81 K,符合预热窑的要求.
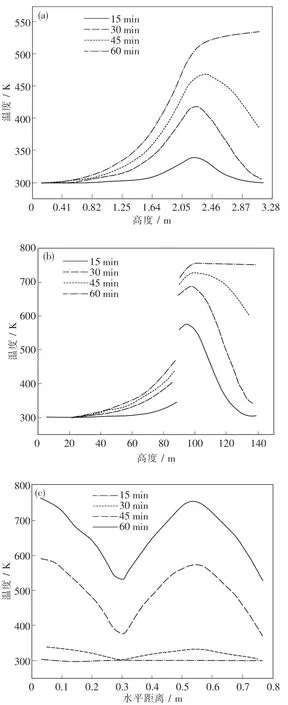
图9 三条线段处的温度曲线Fig.9 Temperature curve at three line segments
4 结 论
(1)高温气体经过进气梁的进气孔时的最大速度为45.27 m/s,实测速度为44.6 m/s,误差为1.51%.
(2)气体入口附近会形成近椭圆形的气体高温区域,气体入口下方的气体温度高于上方的温度;出口附近的气体温度低于400 K,气体的热量利用率高.
(3)高温烟气入口下方的固体存在柱状高温区域,高温区域之间的区域温度约为550.15 K.预热15,30,60 min时固体物料的最高温度分别为585.13,697.09,765.08 K.
(4)预热60 min时,预热窑底部出口的物料温度为524.8~762.29 K,实际生产中预热窑出口处物料最高温度在450~550℃范围内,模拟结果符合预热窑实际工况.
