基于负载随机性的互联网络链路流量识别方法
2021-12-10杨峰,马铭
杨 峰,马 铭
(北华大学大数据与智慧校园管理中心,吉林吉林132013)
1 引言
计算机网络技术的迅速发展,使人们进入了信息时代[1]。由于网络用户数量逐年增长,网络的使用频率不断增加,导致互联网的数据流量呈爆发式上升,造成所使用的网络通信协议混乱、复杂[2]。这些问题给网络管理者带来了巨大压力和挑战,但对网络资源进行管理,优化升级现有网络,需要清楚了解网络中的各类业务应用。因此,网络流量识别越来越受到人们的关注。
目前相关领域大量学者对网络流量识别进行研究,并取得了一定的研究成果,文献[3]通过提取并分析数据流特征,采用集成学习方法构建识别模型,完成网络流量识别。该方法的移动流量识别准确率较高,但识别效率较低。文献[4]利用相对熵特征向量,辨别高低熵值数据流,运用蒙特卡洛仿真方法,评估π值误差,区分局部和整体随机流量,采用支持向量机,输入特征子空间,实现流量识别。该方法能够有效识别加密流量,但识别准确率较低。
针对上述问题,提出了基于负载随机性的互联网络链路流量识别方法,其主要使用数据包负载随机性检测,结合机器学习方法,识别互联网络中的链路流量,所提方法的识别精度和识别效率较高。
2 网络链路流量识别方法
2.1 数据包负载随机性检测方法
采用卡方检验方法检测数据流的随机性。通过比较两种或两种以上的样本率,对两种以上的分类法变量之间的相关性进行卡方检验[5]。比较理论频率与实际频率之间的吻合程度或拟合优度问题,是本方法的基本思路。
由于卡方检验方法属于非参数检验的范畴,分析计数数据时,对总体的分布不作任何假设。通过理论证明,假如n类数据,近似服从卡方分布的统计量可根据实际观察次数A和理论次数T之差的平方与理论次数的商得到,式(1)是该过程的具体表达式

(1)
式(1)为卡方检验的原始理论公式,式内,若想近似效果越显著,那么T的值应越大(T≥5)。实际观察模型和任意现有模型的吻合程度可以采用该公式进行表示,是由于该公式中,卡方值在实际观察次数与理论次数相差越大的条件下越大[6]。卡方值在实际观察次数与理论次数相差越小的条件下越小。
设置total为对象的输出次数,total足够大,且每个观察对象的可能输出结果共有n个,out[0]…out[i]…out[n-1]是其分布表示,其内i=1,2,…,n-2。设置P[i]为对象的每个输出结果out[i]产生的概率,则E[i]=total*P[i]表示其理论观察次数。设置实验中out[i]的实际产生次数为O[i],那么实际观察值和理论推断值间的偏离程度的度量可采用式(2)得出的卡方值表示。若想计算后的x2值的分布和自由度为n的卡方分布近似,那么该对象的观测值应和理论值相同。

(2)

(3)
为增强可信度,推导确定块的卡方值及混合块在某种条件下的卡方值。
1)确定块分析:

=total(2b-1)
(4)

2)混合块分析:


(5)


2.2 基于机器学习的流量识别方法
2.2.1 ID3算法基本思想
采用ID3算法,在数据流数据包负载信息节点中,选择数据流特征属性,利用信息增益来度量数据流特征属性,从而获取最大信息熵增益,以降低数据包负载信息复杂程度,提高识别效率。
假如向量空间中的正例集大小为p,反例集的大小为n,以下两种假设是ID3算法的依据。
1)有穷向量空间E上的一棵准确的决策树,对于随机例子分类几率和E中的正反例几率相同[11-12]。
2)式(6)描述了一棵决策树能准确判断一例子的类别时所需要的信息量表达式

(6)
设置属性A为决策树的根,A包含v个值,{V1,V2,…Vn}将E划分为v个子集{E1,E2,…Ev},假如有Pi个正例和Ni个反例包含于Ei中,则I(pi,ni)表示子集Ei所需的期望信息,以A为根的期望熵如式(7)所示

(7)
式(8)描述了以A为根的信息增益的计算过程
gain(A)=I(P,N)-E(A)
(8)
假如样本集S共有C类样本,Pi(i=1,2,…C)为每类样本数。设置属性A为决策树的根,A包含v个值,{V1,V2,…Vn}将E划分为v个子集{E1,E2,…Ev}。假如pij(j=1,2,…C)为Ei中包含的j类样本数,则子集Ei的信息量E(Ei)如式(9)所示

(9)
式(10)描述了以A为根的信息熵的计算过程

(10)
选取属性A使E(A)最小,获得最大信息增益。
2.2.2 基于机器学习的网络流量识别方法流程
基于机器学习的网络流量识别流程如图1所示。

图1 基于机器学习的流量识别流程
将获取的网络数据流中数据块负载随机性类别作为已标注的数据集,并提取这些数据流的特征属性构成样本集合,利用ID3算法,训练样本集合,构建分类模型并进行预测和估计,完成网络流量识别。
3 实验分析
为了测试所提方法的互联网络链路流量识别效果,在MATLAB实验环境下,采用Wireshark软件的实验室真实网络流量作为实验对象,设置实验数据基本信息如表1所示。

表1 实验数据集
3.1 识别准确率测试
为分析不同数据包个数下的互联网络链路流量识别准确率,设计对比实验,选取140个数据包,分别采用文献[3]方法、文献[4]方法和所提方法进行对比,三种方法的流量识别准确率对比结果如图2所示。

图2 流量识别准确率对比
分析图2可知,当数据包个数达到140个时,文献[3]方法的平均识别准确率为82%,文献[4]方法的平均识别准确率为75%,所提方法的平均识别准确率高达95%,由此可知,所提方法具有较高的互联网络链路流量识别准确性,可将统计数据包个数的窗口值(公式中的total值)设定成60进行流量识别,可进一步提升互联网络链路流量识别的效果。因为所提方法采用卡方检验方法检测数据流的随机性,通过对比不同样本率,分析分类变量关联性,优化理论频数和实际频数的吻合度,从而有效提高流量识别准确率。
3.2 识别效率测试
针对不同数据包个数下,三种方法的互联网络链路流量识别时间对比结果如图3所示。

图3 流量识别时间对比
分析图3可知,随着数据包个数的增加,三种方法的流量识别时间都呈上升趋势。当数据包个数为140个时,文献[3]方法的流量识别时间为3.5s,文献[4]方法的流量识别时间为3.2s,而所提方法的流量识别时间仅为1.7s,相对于其它两种方法,所提方法的流量识别时间较短,识别效率较高。因为所提方法获取基于负载随机性的网络数据流中数据块负载随机性类别,提取数据流的特征属性构成,采用ID3算法样本集合,构建分类模型,能够评估未知数据流量,从而有效缩短流量识别时间,提高识别效率。
3.3 识别漏报率和误报率分析
为了进一步验证所提方法的有效性,分别采用实验分析三种方法,针对表1所示实验数据集对比三种方法的识别漏报率和误报率,结果分别如图4和图5所示。
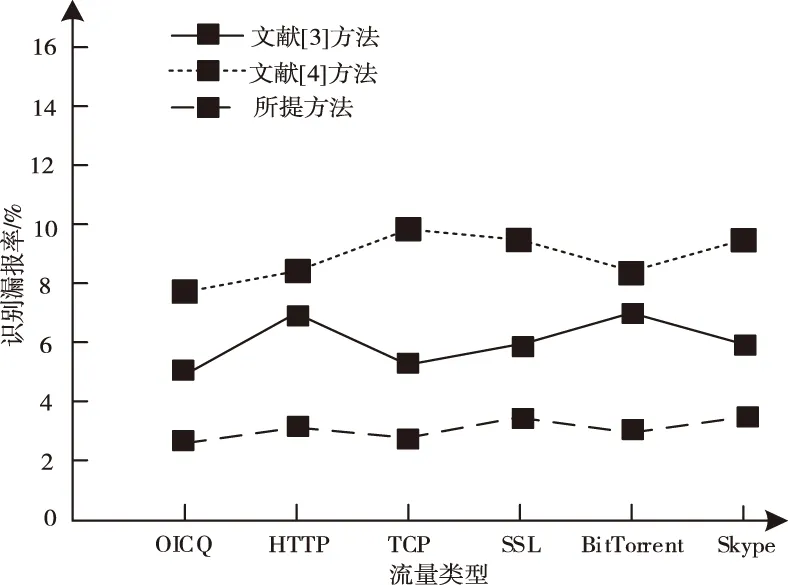
图4 流量识别漏报率对比

图5 流量识别误报率对比
分析图4和图5可知,三种方法进行流量识别产生漏报的概率远大于产生误报的概率,文献[4]方法的漏报率最高可达10%左右,而误报率最高仅有0.25%左右。所提方法与其它两种方法相比,识别漏报率和识别误报率较低,且相对稳定。对比这些数据可以看出,所提方法的互联网络链路流量识别的可靠性较强。
4 结论
为提高网络服务质量和保障网络空间稳定性,提出基于负载随机性的互联网络链路流量识别方法,基于负载随机性,获取网络数据流中数据块负载随机性类别,结合机器学习和ID3算法,实现互联网络链路流量识别。该方法的流量识别误报率和漏报率较低,能够有效提升识别的准确性和效率,确保网络流量稳定性。
