基于观测器误差反馈的换热器自抗扰控制
2021-12-10孙国法刘家铭张兴荣
孙国法,刘家铭,张兴荣
(青岛理工大学信息与控制工程学院,山东 青岛 266520)
1 引言
换热器高度非线性、时滞等不确定性问题存在于所有的工业系统中,是作为影响输出的系统输入而出现的非期望信号,这个问题已经在许多系统中得到了研究[1,2]。通过分析建立系统的模型后分析系统的模型,从模型推导控制律曾是主流思想[3]。但是在建模过程中由于工业环境恶劣同时换热器结垢问题,总是有温度,湿度等难以建模的因素影响几乎是不可能完全了解被控系统的内部信息,但是对模型的抑制系统输出中的干扰是必要的,由于它会影响传感器、执行器、设备的控制结果,发生事故或造成不必要的成本。因此,单纯的通过建模对系统的控制是脱离实际的,在理论研究中抑制或衰减系统输出中的不确定扰动的控制是当前一个比较重要的话题。
随着工业对控制精度和速度要求的增加,不基于模型的PID控制虽能控制住系统[4],但是往往存在输出超调和调节时间的矛盾。因此传统PID已经难以满足控制要求,越来越多的学者企图通过其它方式对系统进行控制[5-7]。由于换热器温度控制过程中存在众多难题,众多学者提出了不同的处理方案。文献[8]通过对加热器的特性和工作机理进行分析,建立相应的数学模型,。将模糊控制技术应用于换热器的出口温度控制系统中进行控制。文献[9] 提出了一种基于级联回收利用技术的新型高温热交换器。根据实验结果,提出并验证了结构设计优化算法。在文献[10]中提出了一种将温度差和湿度差相结合的湿温比参数,并提出了热电流模型来揭示传热传质过程。但是以上研究都对控制系统中原来的不确定性问题考虑不够充分。本文拟通过自抗扰控制思想优先考虑不确定性的优点,解决换热器温度控制问题。
自抗扰技术不依赖精确的被控对象模型,以解决实际被控对象控制不确定性问题为目标,通过把内部干扰和被控对象以外(外扰)不确定性扰动视为总扰动,用扩张的状态实时观测扰动,状态观测器实时估计它后在闭环中进行补偿,由此可以达到一个好的抗扰效果[12],这种思想同样适用于时滞系统,也取得了良好的控制效果,如一阶惯性带有大纯时滞[13],二阶惯性加时滞[14-15],三阶惯性加时滞[16],积分带时滞[17]等系统都已经应用。
但是传统的ADRC都是通过输出反馈提取出未建模或不确定部分的动态信号后在控制器中抵消影响,在控制研究中,由于它需要分别设计、调优和分析控制器和观测器部分,有一定控制难度,同时当参考信号不能对时间求导,但控制器需要此类信号时,原来的控制策略不再适用。
针对以上问题,本文以温度为模型具有不确定时延特性的控制系统为例,将复杂的温度控制系统进行建模对其进行分析,通过基于误差形式的观测器,在参考信号不能对时间求导时,把这些未知的信号可视为总扰动的一部分。这种方法可以在取代微分器的同时大大简化控制设计过程,特别是对于高阶系统。这种方法符合ADRC范式的精神,优先考虑了不确定性。提出了一种利用系统所有信息对自抗扰控制器参数进行整定的方法,并对该方法的性能进行了分析。
2 模型描述及准备工作
本文的控制对象是管状换热器,如图1所示。换热器通过热水预热煤油被控变量是煤油输出温度T12,控制变量是热水质量流量F2。

图1 管式换热器结构
假定换热器的保温条件理想,相同传热系数K12,流体的流量在管内一致,选取煤油出口温度T12为集中参数,并考虑流体流动延迟进行建模。
根据能量动态平衡方程
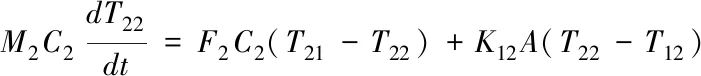
(1)
其中Mi为管内流体质量,Ci为相应流体比热容;A为平均导热面积;Ti为相应的温度,对上式进行简化整理得状态空间方程
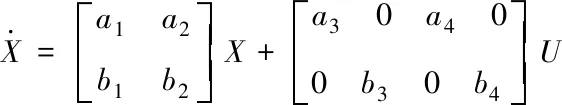
(2)
其中
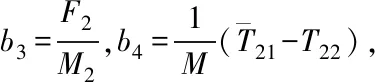
将式(2)表示为传递函数形式
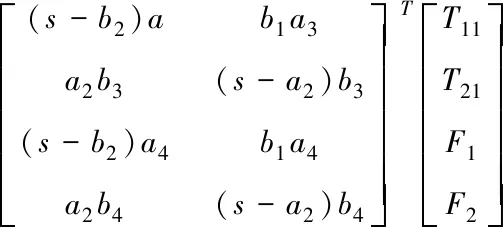
(3)
获取控制系统传递函数
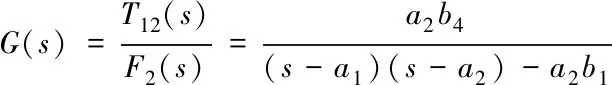
(4)
考虑热传递延时,通过提高阶次法缩短延时时间根据热传递特性,换热器采用三阶惯性带有时延的形式
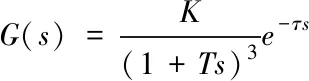
(5)
其中系统增益K,时间常数T,延时时间τ是有区间的动态参数,均可通过相应的阶跃响应辨识出来。其中阶跃响应辨识结果如表1所示

表1 系统参数辨识结果
对式(5)进行拉普拉斯反变换并整理得
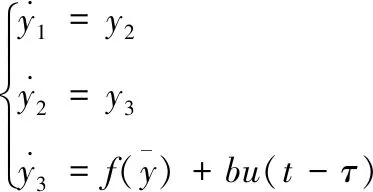
(6)
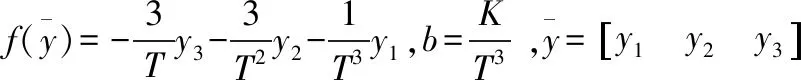
由式(6)可以看出控制量u(t)经过τ时间才能对被控对象起到控制作用,即当前的控制量采用的为τ时间之前计算得出的控制量假定时滞大小τ是采样步长h的整数倍即
τ=kth
(7)
其中,kt为正整数,对此,处理时滞过程如下:
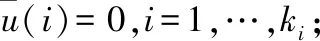
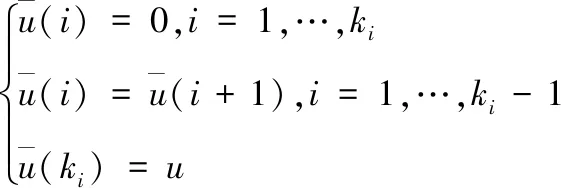
(8)
3 误差状态观测器设计
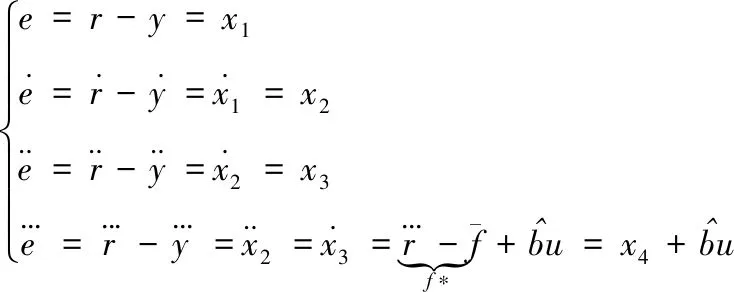
(9)
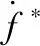
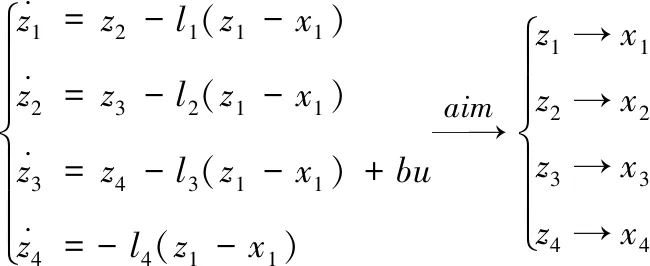
(10)
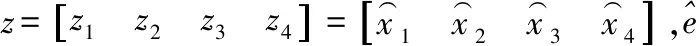
观测器稳定性分析:
定义观测器观测误差
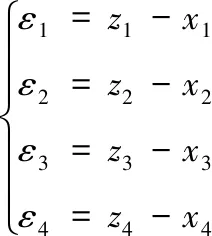
(11)
由式(9)、式(11)可得
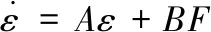
(12)
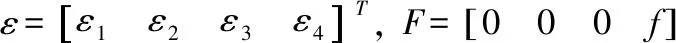
引理:给定矩阵QT=Q>0,存在正定矩阵PT=P>0满足
ATP+PA=-Q
(13)
选用Lyapunov函数
V0=εTPε
(14)
由式(11)(13)得
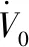
=-εTQε+2εTPBF
(15)
由Young’s不等式可得
(16)
式(15)中λmin(P)λmax(P)表示P的最大最小特征值,λmin(Q)为Q的最小特征值,α>0。
将式(16)带入式(15)可得
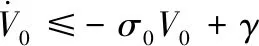
(17)
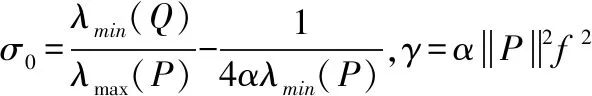
4 控制器设计:
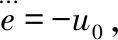
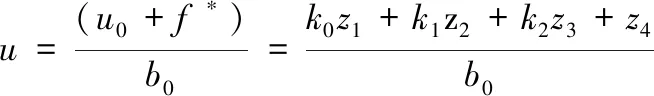
(18)
当观测器稳定后,系统的闭环传函等效为
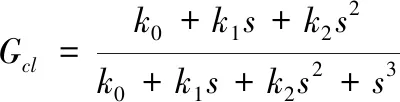
(19)
结合带宽参数化[18]得
k0+k1s+k2s2+s3=(s-(-w))3
(20)
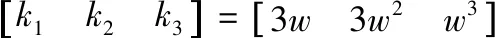
合理的选择w的值即可对系统进行良好的控制。由于实际执行器输出温度存在阈值,所以对控制器限幅
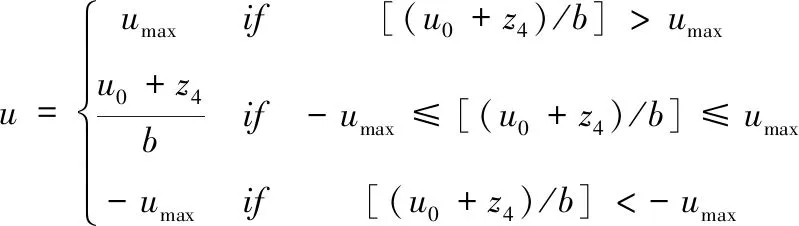
(21)
式中umax为适应执行器输出饱和特性设定的控制信号最大值。
5 仿真算例
为了验证本文的控制方法的有效性,通过Matlab平台对模型控制进行仿真,参考信号分别模拟定点温度设置选取三次温度变化和时变的曲线来测试算法的有效性。
首先选取如下参考信号xr;
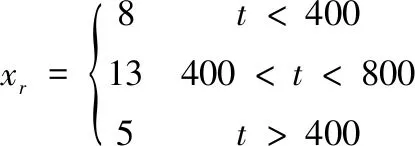
(22)
在仿真中的误差观测器、以及控制器参数选择见表2。
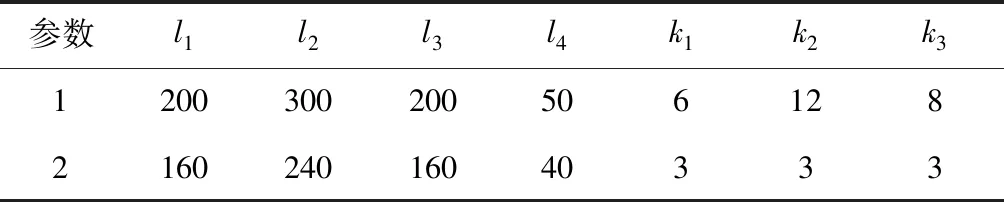
表2 控制算法参数取值表
仿真效果对比见图2。
仿真结果表明两种控制方法都能在有限时间内跟踪上参考信号xr,但是很明显的可以看出PID虽能跟踪上参考信号,但是存在很明显的超调,同时调节时间也比本文提出的控制方法长两倍左右,后者则能精确而快速的跟踪参考信号,当温度设定值改变时,也是迅速反应,几乎无超调跟踪。下面进行动态参考信号特性仿真:
为了验证算法的实时调节性能,选取温度参考信号xr=3sin(0.2t)+2cos(0.3t),响应曲线如图3,同样经过短暂调节参考温度信号能迅速被跟踪,同时确保输出信号得跟踪误差在极小幅度范围内波动,图4为动态调节过程的控制信号。仿真结果表明,当给定温度信号是略复杂信号时,算法通过对观测器的参数的调整,可以将观测误差限制在很小的区间内,短时间稳定后的,观测器能精确地观测出扩张的状态,通过调节控制参数,输出信号能快速的跟踪指定参考信号,由此证明了本文提出的算法的良好的跟踪性能。
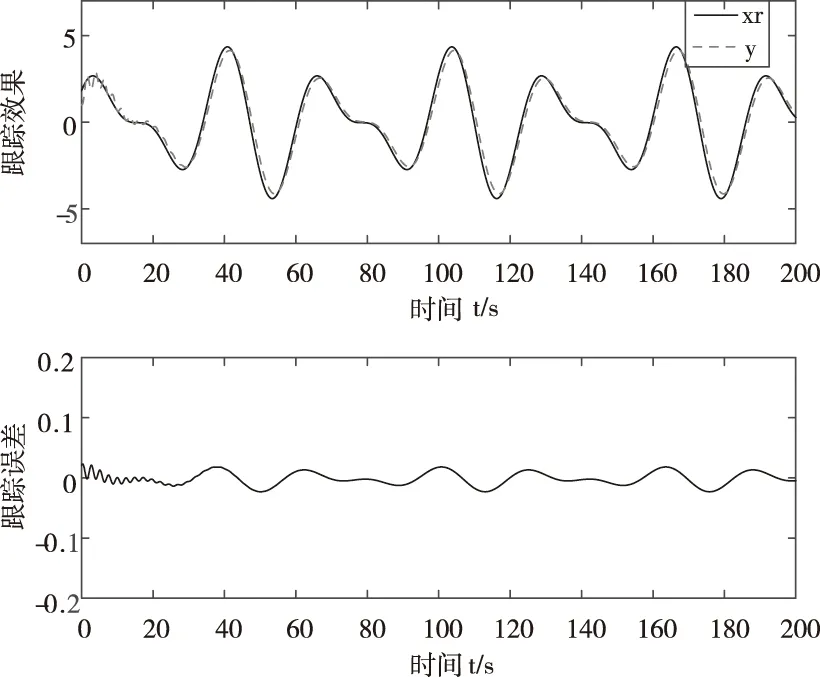
图3 系统输出y跟踪参考信号xr
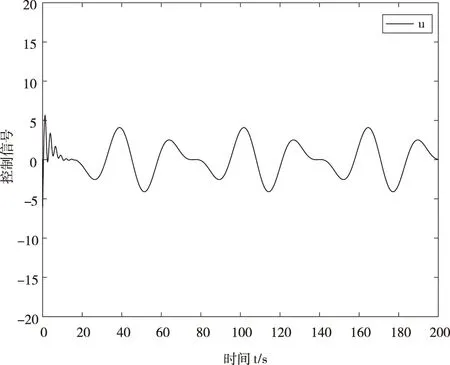
图4 控制信号u
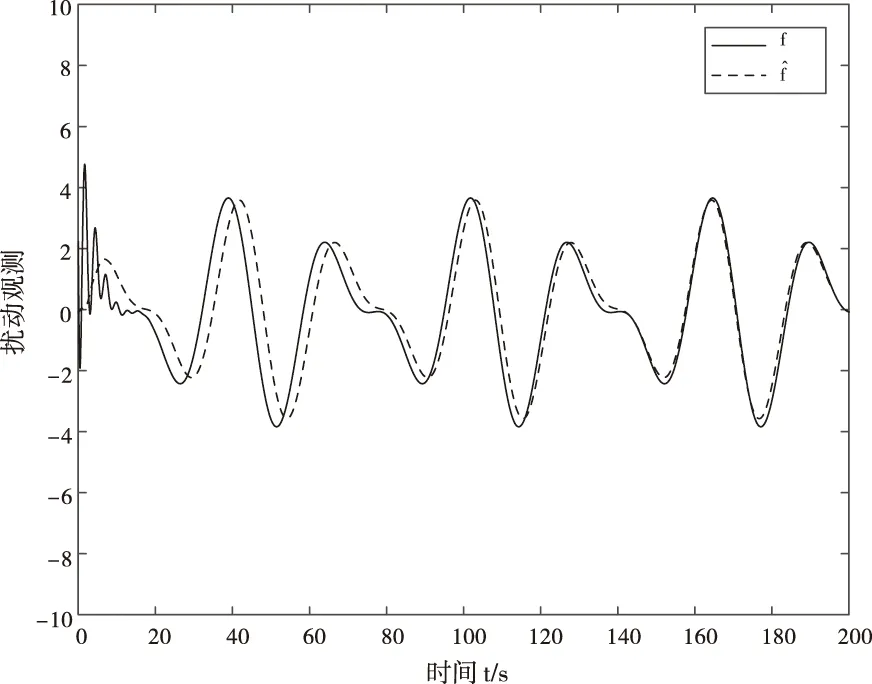
图5 扰动f观测对比效果
6 结论
在本文中,针对有温度控制系统建模并设计了基于误差的扩张状态观测器方法,该方案有明确的物理意义参数整定简单,突出了自抗扰中把不确定性放在首位的思想,在不牺牲控制性能的前提下,有效的简化了控制器调参难题,仿真结果表明该方案有更快的响应时间,参数整定更简单,鲁棒性强等特点。
