基于随机森林算法的IMDB电影评分预测研究
2021-12-10谭家柱
谭家柱
(广西师范大学数学与统计学院,桂林 541006)
0 引言
IMDB(Internet movie database),是一个关于电影演员、电影、电视节目、电视明星和电影制作的在线数据库,IMDB的数据资料中包括了影片的众多信息,如演员、片长、内容介绍、分级、评论等,对于电影评分门目前使用最多的就是IMDB评分。对于喜欢看电影的朋友,去IMDB上寻找好电影是很可取的。IMDB评分核心是基于贝叶斯统计,但本文是基于数据挖掘中的随机森林算法进行探索研究。
1 选题概要
1.1 研究的意义与目标
对于普通人群来说,在经历过白天上班的疲惫后,找一部自己感兴趣且有意义的电影来放松自我是很舒服的一件事情。
本研究的目的是通过已有的真实电影数据集,挖掘出影响电影评分的关键因素,并构建相关预测模型来计算已知测试集中的分类情况,为电影推荐系统给出建议。
1.2 研究的主要内容及步骤
本研究针对“数据世界”官网给出的数据集,其中包括影片出版时间、影片类型、出版地、导演及主演个人信息等28个变量列,利用数据挖掘中的随机森林算法进行电影评分预测模型构建,通过可视化结果分析,找出影响电影评分的关键因素,并为电影推荐系统给出建议。
(1)对数据集进行初步分析,初步判断影响电影评分的变量。
(2)对数据集进行预处理,再分析。
(3)分割数据集。
(4)建立电影评分分类模型。
(5)利用可视化效果分析变量的重要性。
(6)总结影响电影评分的因素,并为电影推荐系统给出可行性建议。
2 数据分析与处理
2.1 电影数据说明(表1)

表1 数据说明
2.2 数据预处理
在Rstudio中根据观察样本数据后,通过检验数据集的数据质量、绘制图表等手段,对电影数据集的结构和规律进行分析。包括缺失值处理、属性规约、数据冗余处理,等。
2.3 数据探索性分析
对强影响变量进行进一步分析。
(1)“imdb_score”与“genres”。新建只含“imdb_score”与“genres”变量数据框,计算不同体裁电影平均得分,结果如图1所示。
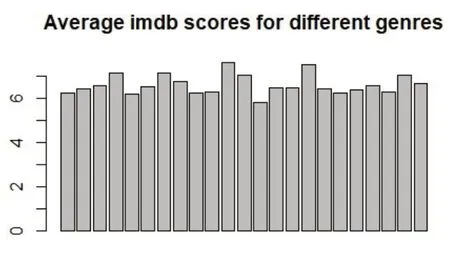
图1 平均得分
由图1可知,尽管电影体裁不同,但电影平均得分均在6~8分(总分10分制)。所以,变量“genres”对本研究电影得分预测无太大影响,故删除。
(2)对“imdb_score”与“aspect_ratio”。对“aspect_ratio”进行频次统计如表2所示。
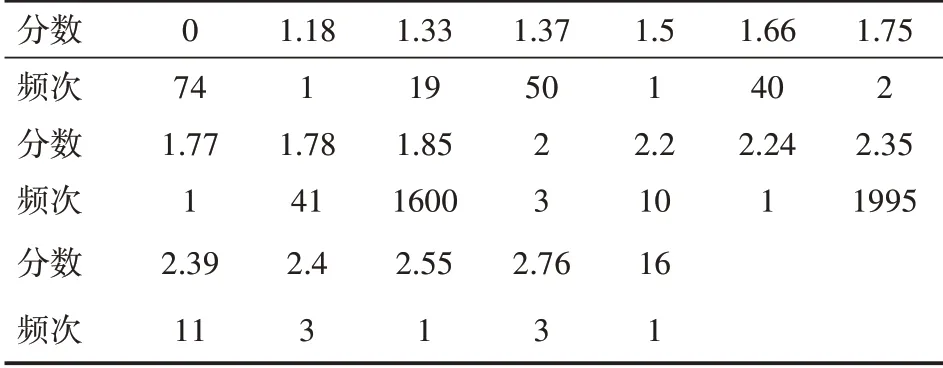
表2 频次统计
由上可知,“aspect_ratio”集中在1.85和2.35,所以我们可以分别计算当aspect_ratio=1.85、aspect_ratio=2.35、aspect_ratio!=1.85&2.35时,“imdb_score”的平均值,分别为6.36355,6.509517,6.694093。从以上输出结果可知,变量“aspect_ratio”对本文电影得分预测无太大影响,故删除。
(3)统计变量“country”频次如表3所示。

表3 频次统计
(4)绘制“title_year”时间序列如图2。
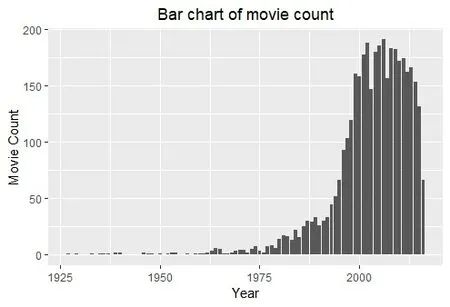
图2 时序分布
观察条形统计图可知,此数据集电影上映年份大概在1975年后迅速增加。所以,截取1975年及以后的电影数据作为新的数据集。
(5)绘制利润前20名电影“budget”与回报率关系如图3。
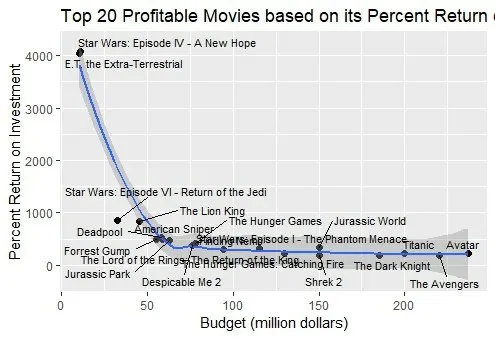
图3 利润
观察上述拟合曲线可知,当成本逐渐增加时,利润率趋于平稳。
(6)绘制利润前20名电影“gross”与“im⁃db_score”二维图如图4。
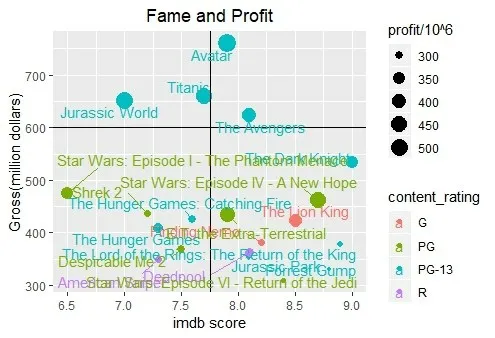
图4 二维分布
观察上图可知,大多数imdb评分高的电影票房收入大部分不出众。
(7)绘制“movie_fb_likes”与“imdb_score”关系图,以“content_rating”分类如图5所示。
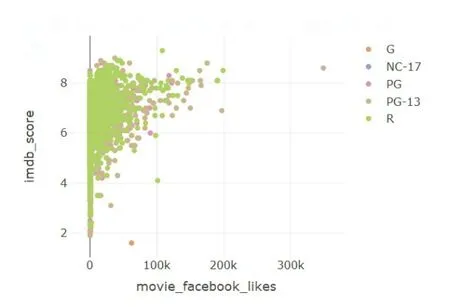
图5 分类
由上图可知,“movie_fb_likes”越多,imdb评分越高,变量比较重要。
(8)删 除 变 量“profit”、“return_on_invest⁃ment_perc”
(9)将变量“imdb_score”划分为5类:(0,2)、(2,4)、(4,6)、(6,8)、(8,10)
2.4 变量相关性分析
(1)用两个指标变量样本间的pearson相关系数来估计2个指标变量总体间的pearson相关系数[1],其计算公式为:
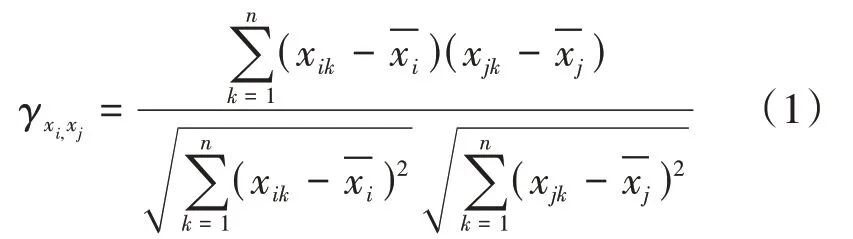
(2)绘制剩余变量的二维pearson相关系数图如图6所示。
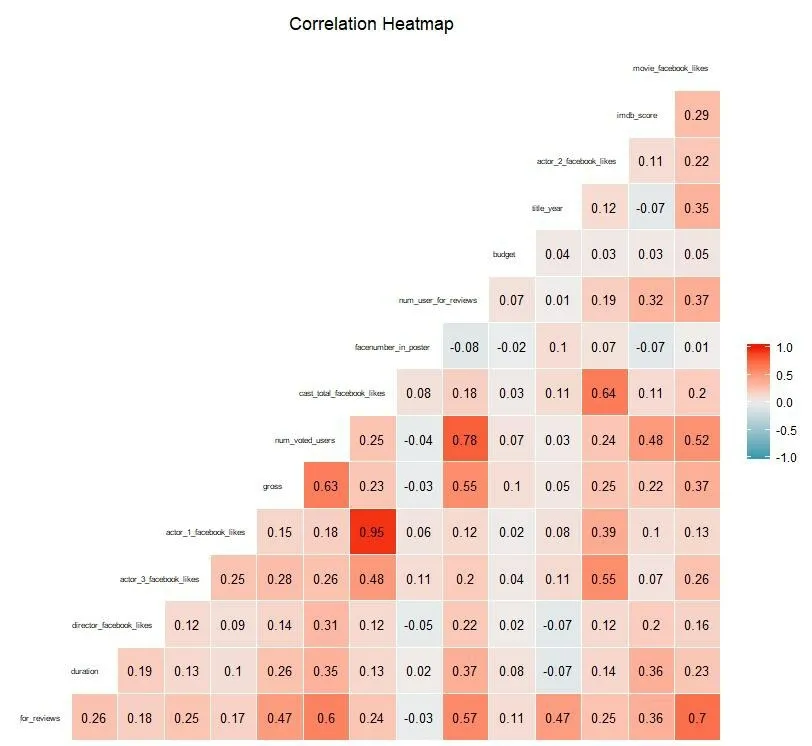
图6 二维相关系数
由图6可知,某些变量之间相关程度很高(pearson系数超过0.75),会造成高度线性相关,影响模型预测。
(3)删除pearson系数表中高度相关变量。
(4)重新绘制剩余变量的二维pearson相关系数如图7所示。
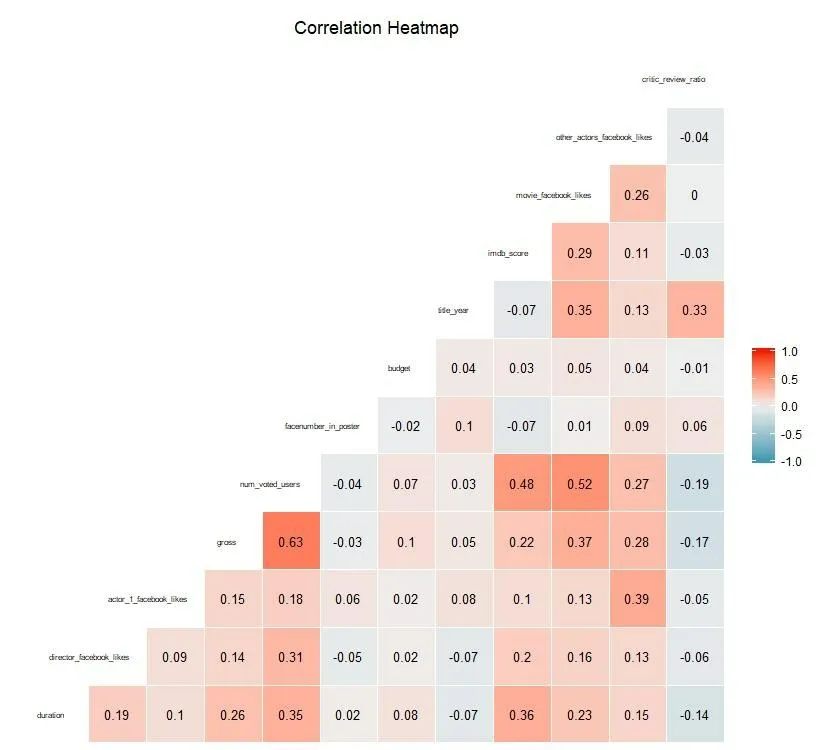
图7 二维相关系数
由上图可知,某些变量之间相关程度很高(pearson系数均未超0.7),变量相关性良好。
(5)剩余指标变量15个,如表4所示。
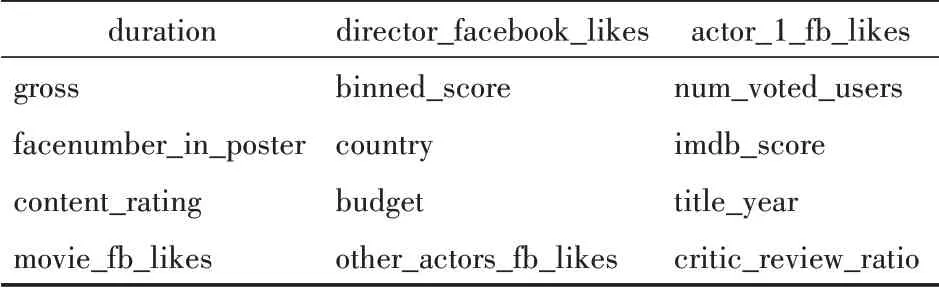
表4 剩余指标变量
3 随机森林、BP神经网络介绍
3.1 随机森林集成学习概况
(1)随机森林于2001年由Leo Breiman提出,它首先通过自助法(bootstrap)采样技术,从大小为N的原始训练样本集中随机有放回并重复抽取k个样本,生成新的训练样本集。其次根据自助样本集生成k个分类树组成随机森林,新数据的分类结果视分类树投票分数而定。其实质是对决策树算法的一种改进,将多颗决策树合并在一起,每棵树的建立依赖于一个独立抽取的样品,而且森林中的每棵树都具有相同的分布,分类误差将取决于每一棵树的分类能力和它们之间的相关性。
特征选择采用随机的方法分裂每一个节点,然后比较不同情况下产生的误差。通过检测到的内在估计误差、分类能力和相关性决定选择特征的数目(特征选取数目一般为最终指标变量数进行开方)。单棵树的分类能力可能很小,但在随机产生大量的决策树后,一个测试样品可以通过每一棵树的分类结果经统计后选择最可能的分类[2]。
3.2 随机森林算法
(1)设原始训练集为N,应用bootstrap法有放回地随机抽取k个新的自助样本集,并由此构建k棵分类树,每次未被抽到的样本组成了k个袋外数据。
(2)设有X个变量,首先在每一棵树的每个节点处随机抽取m个变量,然后在m中选择一个最具有分类能力的变量,变量分类的阈值将通过检查每一个分类点确定。
(3)每棵树最大限度地生长,不做修剪。
(4)将生成的多棵分类树组成随机森林,用随机森林分类器对新的数据进行判别与分类,分类结果按树分类器的投票多少而定。
流程图[5]如图8所示。
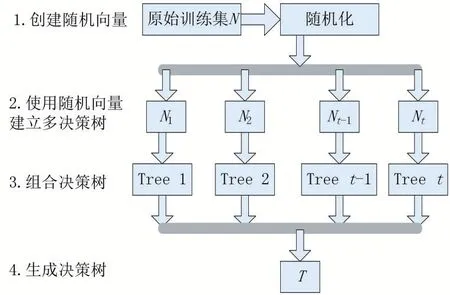
图8 流程分布
3.3 随机森林性能评估
(1)由理论知识证明可知,当树足够大时,随机森林的泛化误差上限收敛于:

其中是树之间的平均相关系数,s是度量树型分类器的“强度”的量。一组分类器的强度是指分类器的平均性能,而性能以分类器的余量M用概率算法度量:
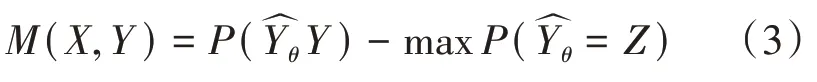
其中X≠Y,是根据随机向量θ构建的分类器对X做出的预测类,余量M越大,分类器正确预测给定的样本X的可能性就越大[5]。
(2)OOB(袋外数据)。在随机森林bagging法中可以发现bootstrap每次约有1/3的样本不会出现在bootstrap所采集的样本集合中,故没有参加决策树的建立,这些数据称为袋外数据OOB,用于取代测试集误差估计方法,可用于模型的验证。
(3)混淆矩阵。混淆矩阵是用来评价分类器性能的一种特殊矩阵[5],其形式如表5。

表5 混淆矩阵
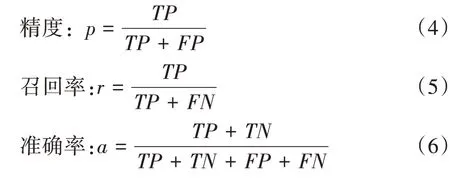
其中精度和召回率是两个广泛使用的度量,用于成功预测一个类比预测其他类更加重要的应用。
3.4 BP神经网络原理
(1)BP神经网络的学习过程由信号的正向传播与误差的反向传播两个过程组成。
(2)正向传播时,输入样本从输入层传入,经隐层逐层处理后,传向输出层。若输出层的实际输出与期望输出不符,则转向误差的反向传播阶段。
(3)误差的反向传播是将输出误差以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。
(4)BP网络由输入层、输出层和隐层组成,N为输入层,P为输出层,Q为隐层。BP神经网络的结构如图9[6]所示。
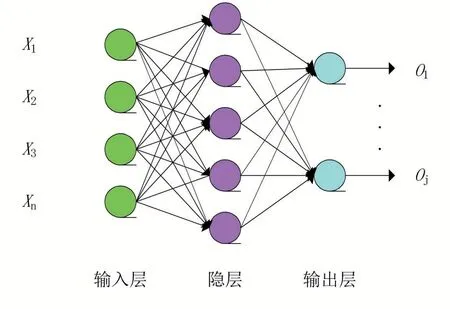
图9 BP神经网络结构
4 分类预测模型
4.1 建立随机森林模型
调用randomForest函数包进行训练调参,误差估计如图10所示。
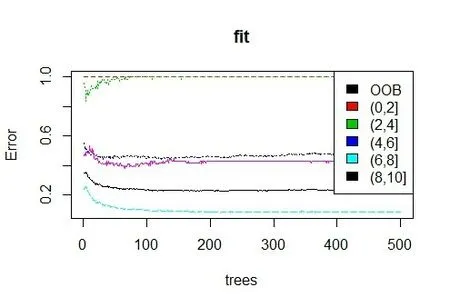
图10 误差估计
4.2 调参表
(1)训练集以75%和25%比例切割,mt ry=4,输出结果如表6所示。
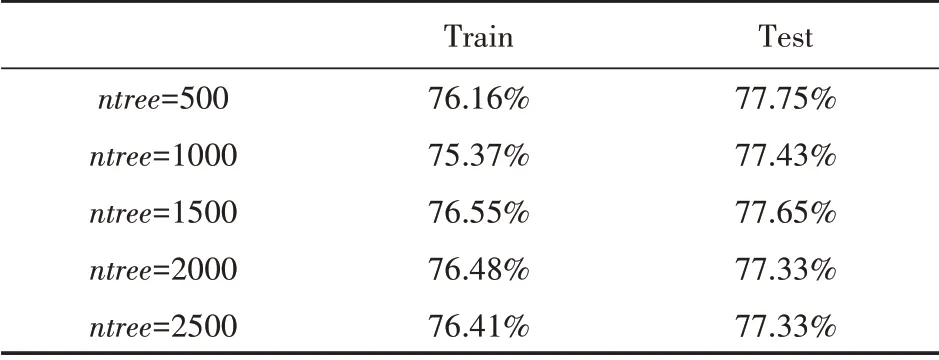
表6 输出结果
(2)训练集以80%和20%比例切割,mtr y=4,输出结果如表7所示。
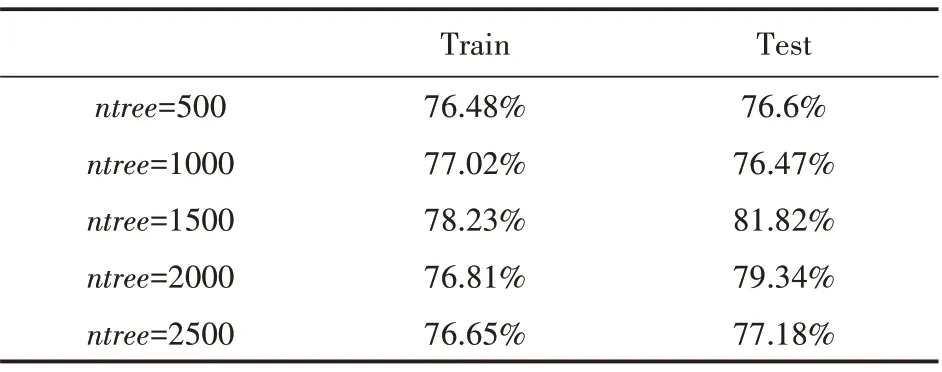
表7 输出结果
(3)训练集以70%和30%比例切割,mtr y=4,输出结果如表8所示。
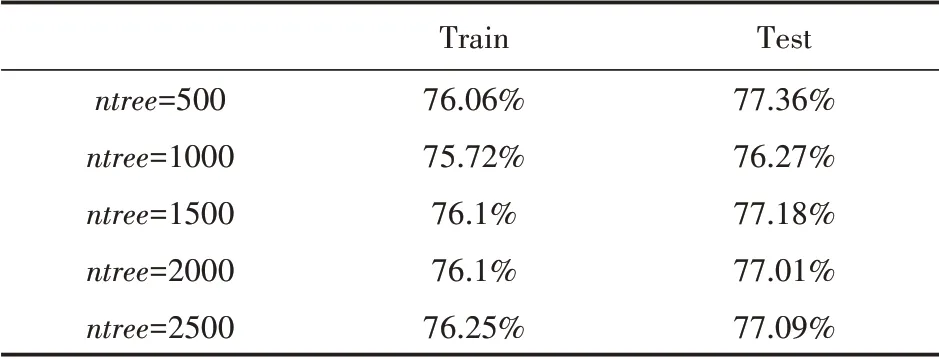
表8 输出结果
综合上述可知,当训练集以80%和20%比例分割,mtr y=4、ntree=1500时,模型分类预测准确率较好,为81.82%。
4.3 Gi ni指数衡量变量的重要性
根据“MeanDecreaseGini”来度量各变量重要性,可视化结果如图11所示。
从图11可以看出,指标变量“conten_rat⁃ing”、“facenumber_in_poster”、“country”重要性程度不高,指标变量“num_voted_users”、“dura⁃tion”、“budget”等重要性程度较高。这一结果也符合猜想。
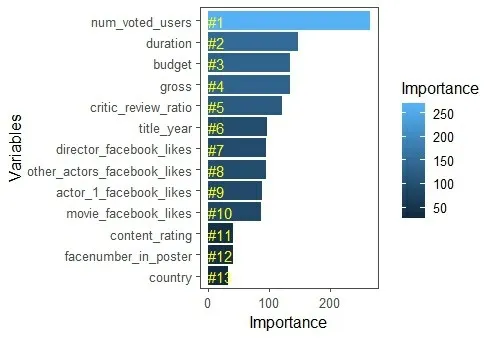
图11 可视化
4.4 建立BP神经网络模型
调用nnet函数包对数据集按不同比例切割后进行建模调参,调参结果如表9所示。

表9 调参结果
由测试结果可知,当数据集切割比例为8:2时,分类准确率为74.47%,较高。
4.5 Fr i edman检验模型分类性能
(1)Friedman检验原理。假定用四个数据集对算法进行比较。先使用留出法或者交叉验证法得到每个算法在每个数据集上的测试结果,然后在每个数据集上根据性能好坏排序,并赋序值1,2,…;若算法性能相同则平分序值,继而得到每个算法的平均序值,算法比较序值参见文献[7]。
(2)算法性能检验标准。①根据Friedman检验,如果上述四个算法性能都相同,则它们的平均序值相同。②如若不同,则引入以下通用变量进行判别(k为算法个数,N为数据集个数):
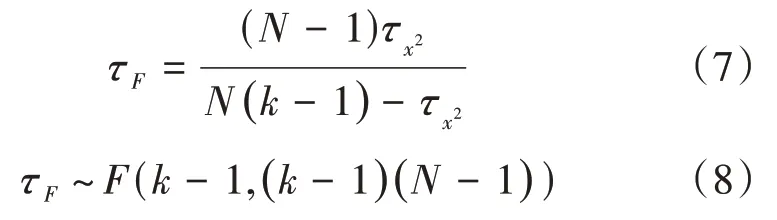
其中,
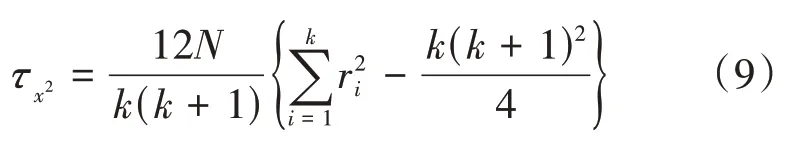
(3)当置信水平α=0.05时,F检验常用临界值参见文献[8]。
(4)采用四折交叉验证,计算可得:τF=1,明显小于临界值F(1,3)=10.13,故接受原假设“所有算法的性能相同”。
(5)综合比较上述四折检验结果,用随机森林分类模型进行评分预测准确度较好。
4.6 随机森林模型预测
在新电影数据集中利用随机无放回抽样抽取15部电影进行评分预测如表10所示。
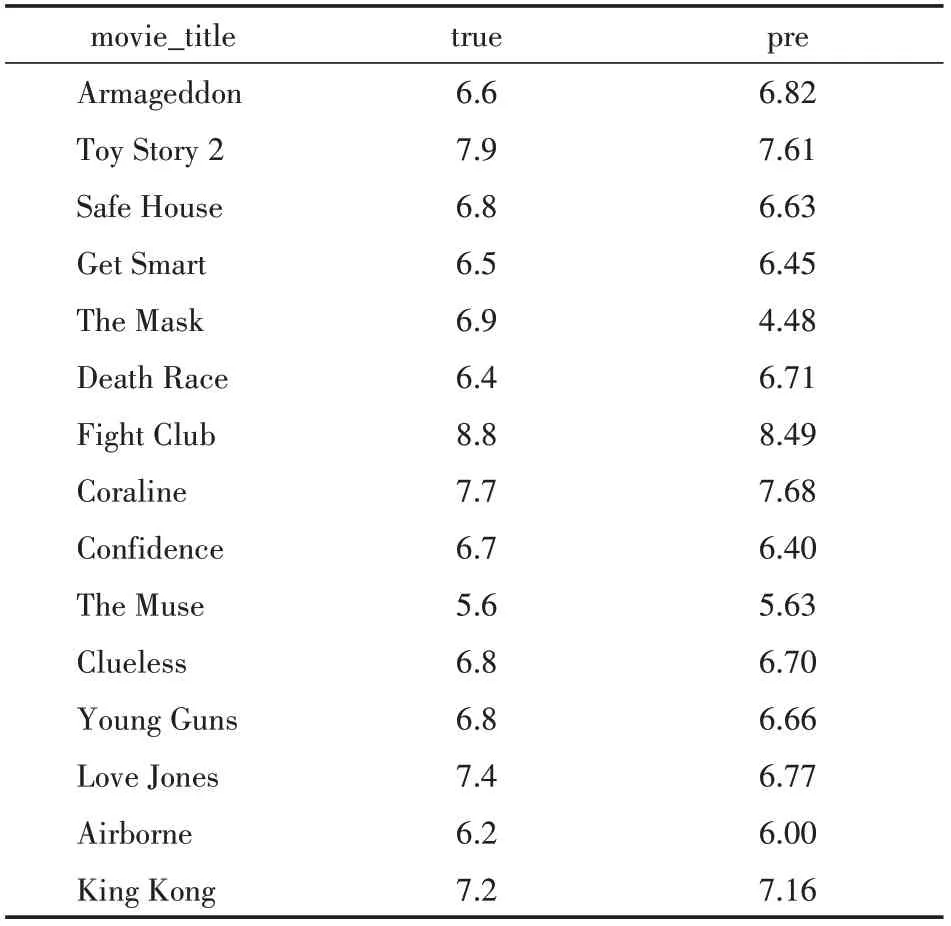
表10 预测结果
分析表10可知,电影评分预测效果较好。
5 结语
(1)随机森林在运算量没有显著提高的前提下提高了预测精度。
(2)随机森林算法鲁棒性好,对于离散数据点相对而言不敏感,由于电影信息多样性,难免会有噪声数据,随机森林算法能有效地避免这些轻微噪声数据对最终模型的影响[3]。
(3)对于本研究所使用的数据集,变量之间可能会产生多元共线性。但随机森林对多元共线性不敏感,结果对缺失数据和非平衡数据比较稳健,被誉为当前较好的算法之一[4]。
(4)本文将机器学习应用在电影评分预测领域,通过票房、评论率等指标变量作为影响电影评分的特征,对其进行特征处理,能为大众推荐电影提供有价值的参考,具有实际意义。
