文化自信视域下“初等数论”课程思政教学的探索与实践

孙庆括，徐向阳，潘 腾

2020年5月，教育部印发的高等学校课程思政建设指导纲要明确提出，全面推进课程思政建设是落实立德树人根本任务的战略举措.落实立德树人根本任务，必须将价值塑造、知识传授和能力培养三者融为一体、不可割裂.同时，高校课程思政要融入课堂教学建设全过程，落实到教案、课堂授课、教学研讨、作业论文等各环节［1］.因此，在承担卓越教师培养角色的“初等数论”教学中开展课程思政教学探索显得尤为迫切.然而，长期以来，我国中小学和大学数学课程均受移植于西方数学的影响，造成很多学生了解中国数学文化程度不够，文化自信彰显不足.事实上，“初等数论”课程是高师院校数学与应用数学专业一门必修的专业基础课程，主要研究整数的性质及基本理论，与中小学数学有着密切的联系.像小学数学教材“数学广角”中有大量的数论内容，高中阶段已把“初等数论”课程初步列为选修系列模块课程.因此，从文化自信的视域进行“初等数论”课程思政教学改革意义更加特殊.不仅可以突破师范生头脑中原先固有的西方数学文化中心的数学观，还可以让未来的“准教师”们树立牢固的文化自信观念，增强民族自豪感、自尊心和自信心，以便将来从事中小学数学教学的过程中潜移默化的坚持以文化人、以文育人，让下一代更好赓续中国优秀文化.

1 文化自信视域下“初等数论”课程思政元素的挖掘途径

1.1 从讲述中国数学家爱国故事层面，挖掘家国情怀思政元素

家国情怀是中华民族生生不息的文化基因，是我国优秀传统文化的宝贵精神财富，更是中华文明之所以能历经多次磨难而不灭的不竭动力.因此，“初等数论”课程可以充分利用数学家爱国故事作为传播中国传统文化精神和厚植家国情怀的重要课程思政元素.比如在绪论部分介绍数论发展史时，除介绍西方数论代表人物外，还可以重点可以介绍我国数论大师华罗庚先生，在抗日战争期间放弃美国优越的生活和科研环境，克服重重困难回到祖国怀抱，并在归国途中给留美学生写公开信，号召大家回国参加新中国建设，投身我国数学科学研究事业的家国情怀.

1.2 从讲述中国数学家自强不息奋斗的民族精神层面，挖掘坚定理想信念思政元素

奋斗精神是中华民族的宝贵财富.习近平总书记指出，“我们的国家，我们的民族，从积贫积弱一步一步走到今天的发展繁荣，靠的就是一代又一代人的顽强拼搏，靠的就是中华民族自强不息的奋斗精神”.因此，传播中华民族的自强不息奋斗精神是“初等数论”课程的重要使命，可以充分利用中国数学家砥砺奋斗的感人事迹进行坚定中国特色社会主义道路的理想信念教育.比如在讲解“素数”时，不仅可以介绍华罗庚先生在昆明的一个吊脚楼上的艰苦环境中写出被称为20世纪经典数论著作堆垒素数论，且发表40多年来其主要结果仍居世界领先地位，先后被译为俄、匈、日、德、英文出版的事迹.还可以介绍陈景润先生凭借其对数学的热爱和坚强的毅力，克服种种困难，在十分艰苦的条件下攻克了世界著名数学难题“哥德巴赫猜想”中的“1+2”［2］，在中国科学上发表了名为《大偶数表为一个素数及一个不超过两个素数的乘积之和》的震撼全世界的学术论文，成为研究“哥德巴赫猜想”发展史上里程碑的事件.

1.3 从展示中国辉煌的数论发展历史视角，挖掘爱国主义思政元素

学科发展历史由于其自身的特殊属性，历来是进行学科德育的有效途径，也是课程思政教育的重要载体.事实上，我国是世界上最早采用十进位制的国家，算筹、珠算盘等数学工具很早就开始产生、应用和发展，九九表和一些其他数论内容就记载在我国古代的算书上，是我国古代数学辉煌成就的重要组成部分［3］.像孙子算经、数书九章、张邱建算经等经典数学名著中就充满着大量的数论内容.比如讲解“同余”及“同余方程”章节时，就可以上述著作中与有关同余方程的历史名题及求解思想.特别是重点讲解秦九韶在数书九章中创立的“大衍求一术”求解一次同余式组的算法及思想内涵，该算法在数学界也被称为“中国剩余定理”.而欧洲直到德国数学家高斯于公元1801年出版的算术探究中才明确地写出了“中国剩余定理”［4］.因此，在“初等数论”课程中可以充分利用我国数论辉煌成就发展史进行爱国主义和文化认同教育.

1.4 从古代东西方两种数学思想体系比较视角，挖掘辩证唯物主义和道路自信思政元素

国际上对以欧几里得几何为代表的西方古代以演绎公理体系为中心的数学思想体系公认较早，而对以九章算术为代表的东方古代以计算和算法为中心的数学思想体系的认同则相对较晚［5］.因此，在早期国际数学史界并不承认有个东方数学思想体系，谈到数学史则只限于西方的数学.比如美国M.克莱因所著的国际公认的数学史名著古今数学思想，在全书51章中只有第9章“印度和阿拉伯的数学”才涉及到一点传统的东方数学，但他竟然认为在数学史上，希腊人的后继者是印度人，印度的数学只是在受到希腊数学成就的影响后才颇为可观，对在数学方面有着光辉历史的中国只字不提［6］.另外，加上近现代我国大学数学教科书受移植于西方的影响，从而导致部分大学生对中国古代算法为中心的数学思想体系了解不够透彻.事实上，古代东西方两种数学思想体系各有所长，互为补充，东西辉映.在数学发展的历史长河中曾多次反复互为消长，交替成为数学发展中的主流.特别是东方数学思想体系在明清几百年的相对消沉后，由于现代计算机的出现，已越来越受到重视.因此，在讲授“初等数论”课程时要对涉及到的有关中国古代算法思想的内容，要重点对古代东西方两种数学思想体系进行比较，挖掘其中蕴含的中国传统文化思政元素.比如在讲解求“最大公因数”方法时，除介绍辗转相除法外，还可以重点介绍九章算术中的“更相减损术”原理，对我国古代数学的算法思想体系进行介绍，还可以引导学生对古代东西方两种数学思想体系进行讨论，从而培养学生的道路自信.

2 文化自信视域下“初等数论”课程思政教学的实施路径

2.1 围绕“课程思政”目标重新优化教学内容

理想的课程内容设计应该是融知识性、思想性、教育性与文化性于一体.因此，基于此原则，根据高等学校课程思政建设指导纲要要求和数学与应用数学师范本科专业培养目标，结合我校48学时实际情况，把闵嗣鹤、严士健主编的主讲教材《初等数论》（第四版，高等教育出版社，2020）分为6个部分，每部分内容均设计了不同的课程思政元素（表1），并有机融入课程教学，达到润物无声的育人效果.

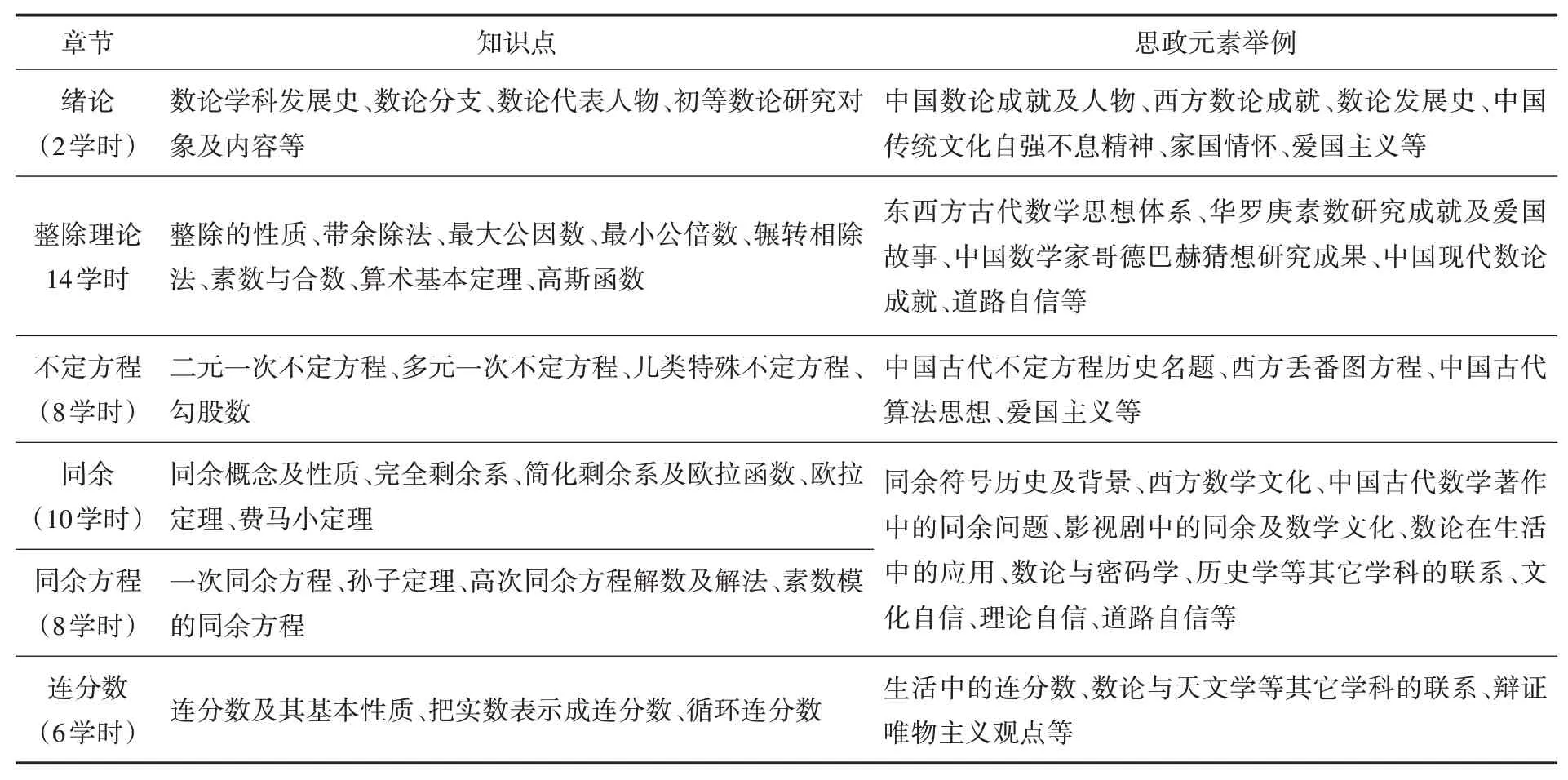
表1 “初等数论”课程教学内容与思政元素融合一览表

2.2 开发多种思政元素融合的教学设计

如何开发有效的教学设计将思政教育与专业教育有机融合，是发挥“课程思政”育人功能的关键环节.而设计有效可行的教学过程又是课程思政教学的关键.针对不同的知识内容，从中国数论发展成就、中国传统文化自强不息精神、家国情怀、爱国主义、东西方古代数学思想体系、道路自信、坚定理想信念等思政元素开发教学设计.进一步，充分考虑学生接受特点，以学生为主体，采用在线预习、文化呈现、讨论辩论、过程渗透、引申总结等方式展开教学互动，以便达到最佳的课程思政育人效果.下面以“同余的概念及其性质”一节为例加以说明（表2）.

表2 “同余概念及基本性质”思政教学设计案例

2.3 构建线上线下混合的参与式教学模式

传统的“初等数论”课堂教学大多采用以教师为主的讲授式教学，学生是被动的信息接受者，参与度普遍不高.基于此种现实情况，构建了线上线下混合的参与式教学模式.首先在超星学习通建设内容丰富的线上课程资源，上传了大量具有反应中国数学文化思政元素的视频、文章、书籍等，供学生课前在线预习使用.同时，精心优化教学过程，构建了以“问题引领、主动参与、互动生成、生动发展”为特征，以“情感参与、思维参与、行为参与”为途径，以“文化驱动——数学化理解——多领域渗透——总结提升”为流程的思政教学模式（图1）.其中“数学化理解”与“多领域渗透”是该模式的核心，充分发挥中国数学文化的课程思政功能［7］.

图1 基于文化自信的“四段八环”参与式教学模式

2.4 实施凸显过程性与文化性融为一体的多元化考核评价

构建科学、全面的教学评价体系是衡量课程思政建设成效的重要指标，评价体系的完善与否一定程度上制约着课程思政的教学效果.因此，本着全方位育人、全过程考核的理念，采用客观量化评价与主观效度检验相结合的方式，注重过程性评价（表3），力求教学中注重学生的知识、能力、情感、态度和价值观的发展情况，及时和充分反映学生的成长情况，达到知识传授与思想启迪、价值引领相结合的课程思政教学目标，彰显教学评价的人文性和综合性［8］.另外，改革期末试卷题型结构，增加情境性题目，把中国数论成果、数论与其它学科的联系等思政元素引入试题.

3 结语

专业课是课程思政建设的基本载体.如何结合课程特点、思维方法和价值理念，深入梳理专业课教学内容，挖掘课程思政元素，有机融入课程教学是专业课思政教育的重要内容.从文化自信的视域入手，从四个方面系统梳理了“初等数论”课程中蕴含的五种思政元素，并将相关思政元素有机融合到教学设计和课程考核评价体系中去，取得了良好的教学实践效果.然而，课程思政建设是一个长期和系统性的工程，如何构建科学合理的课程思政教学体系，如何打破长期以来思想政治教育与专业教育相互隔绝的“孤岛效应”，解决好专业教育和思政教育“两张皮”问题，仍然需要做大量细致的教学实践检验工作.因此，后续将根据教学反馈，并借鉴其它课程思政教学改革的成功经验，进一步挖掘“初等数论”课程思政元素和素材，不断创新教学设计，改进教学模式和方法，完善考核评价体系，更好地践行立德树人的教育目标，从而达到全面提升师范生文化自信的价值引领目的.

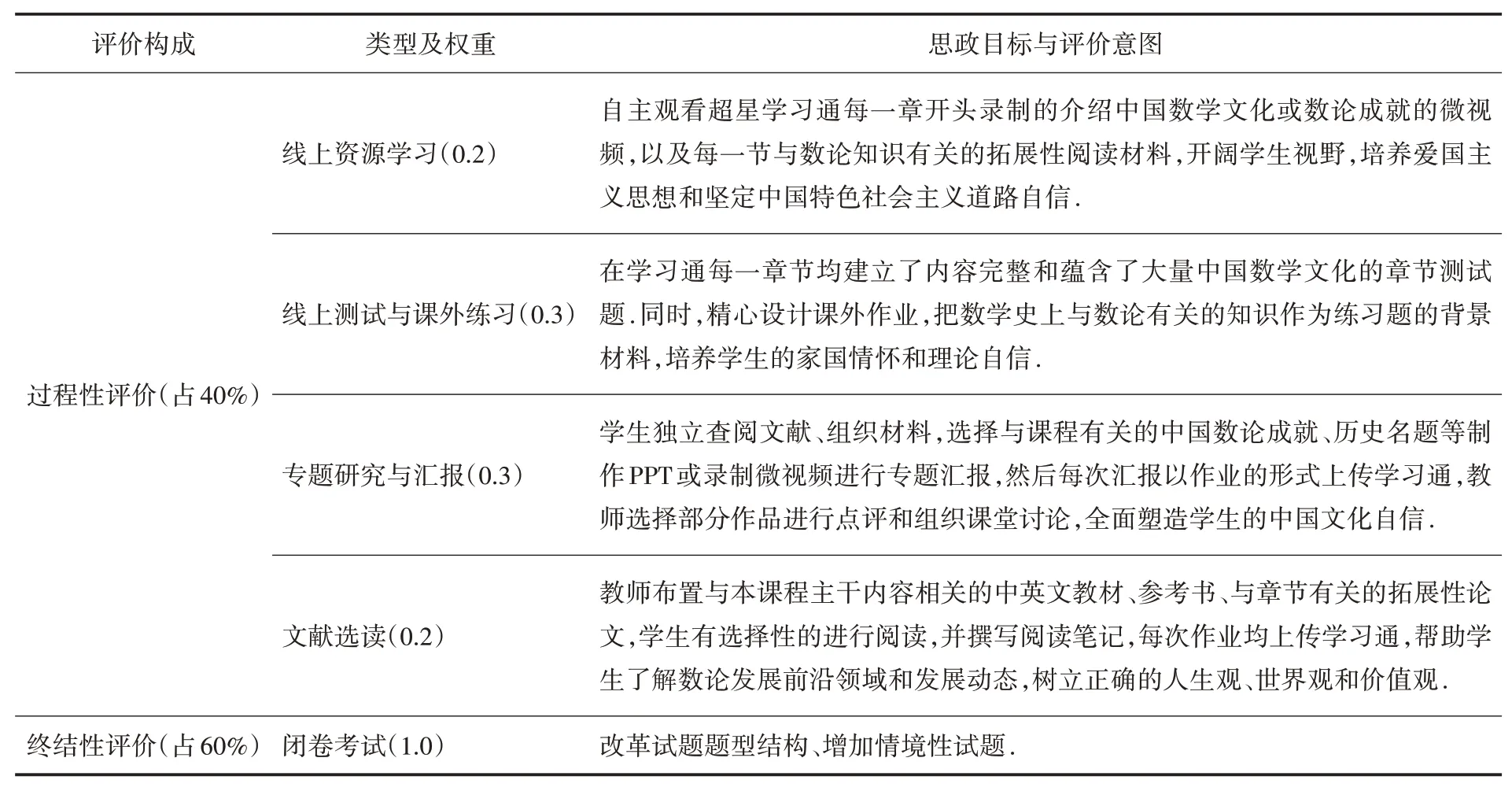
表3 “初等数论”课程思政教学考核评价指标体系