NARMA-L2模型的改进及其神经网络自校正控制器
2021-12-09侯小秋李丽华
侯小秋, 李丽华
(黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)
0 引 言
自校正控制器算法有诸多学者研究,张婧[1]提出一种基于非均匀采样系统的自校正控制方法。胡成才[2]针对新型灰箱系统模型,给出了新型切换自校正控制算法。赵栎等[3]研究了确定性多变量系统的自校正控制器算法的收敛性﹑鲁棒性及稳定性。诸多学者研究传统NARMA-L2模型的神经网络控制的应用,汪权等[4]应用NARMA-L2控制地震作用下高层建筑结构的振动。闫召洪等[5]将NARMA-L2模型应用于控制航空发动机推力衰退缓解。刘仕兵等[6]指出了NARMA-L2模型的弓网系统振动主动控制效果较好。笔者提出一种改进NARMA-L2模型,研究其神经网络自校正控制器。
1 改进NARMA-L2模型
非线性NARMA模型为
y(t+d)=f[y(t),y(t-1),…,y(t-ny),
u(t),u(t-1),…,(t-nu)],
(1)
式中:y(t)——系统输出;
u(t)——控制输入;
f(·)——非线性函数;
ny、nu——阶数;
d——时滞。
令
M=[y(t),y(t-1),…,y(t-ny),
u(t-1),u(t-2),…,u(t-nu)]。
将式(1)在零工作点处一阶泰勒展开
f[M,u(t)]=f(M,0)+
式中,R[M,u(t)]——泰勒展开余项。
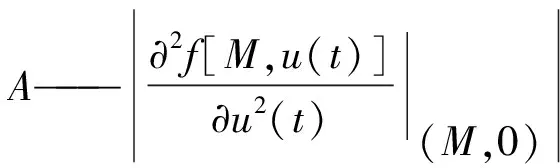
因u(t)有界,故R[M,u(t)]较大,文中提出一自适应滤波动态工作点,
u0(t)=θ(q-1)u(t-1),
式中:u0(t)——自适应滤波动态工作点;
θ(q-1)——加权网络。
θ(q-1)=θ0+θ1q-1+…+θnθq-nθ。
满足约束条件
0≤θ(1)≤1。
在u0(t)处对式(1)进行一阶泰勒展开
f[M,u(t)]=f[M,u0(t)]+
R[M,u(t)-u0(t)],
(2)
则

在系统运行的多数时刻
R[M,u(t)-u0(t)] 式(2)可写成改进的带误差补偿的NARMA-L2模型为 y(t+d)=f0(M)+g0(M)· [u(t)-u0(t)]+ye(t+d,M), f0(M)=f[M,u0(t)], ye(t+d,M)=R[M,u(t)-u0(t)]。 (3) 式中:W、V、H——BP神经网络的连接权重值向量; 选取广义目标函数 (4) 式中:r(t) ——参考输入; λ(q-1) ——加权网络。 λ(q-1)=λ0+λ1q-1+…+λnλq-nλ, 式中,nλ——阶数。 (5) [u(t)-u0(t)], (6) 则可调参数向量 ηT=[WT,VT]。 式(5)两边对W的分量wi求偏导得 (7) (8) 式(5)两边对V的分量vj求偏导得 (9) (10) 式(6)两边对wi求偏导得 (11) 式(6)两边对vj求偏导得 (12) (13) 式(7)两边对vj求偏导得 (14) 式(9)两边对wi求偏导得 (15) 式(9)两边对vi求偏导得 (16) 式(11)两边对wj求偏导得 (17) 将式(11)两边对vj求偏导得 (18) 将式(12)两边对wi求偏导得 (19) 将式(12)两边对vi求偏导得 (20) 参考文献[7]的直接极小化指标函数的自适应优化算法,可得W、V的在线学习算法,选取目标函数为 式中:α——加权因子; g*(·)——目标函数。 W、V的在线学习算法为 λ2(t)-Q(t-1)}, ρ(t)——收敛因子; Q(t)——Hessian矩阵; λ(t)——权重对角矩阵。 Q(t)求逆及克服算法病态的权重对角矩阵λ(t)的确定,可参考文献[8]的算法。 估计误差 目标函数为 λe(t)——权重对角矩阵; ge(H)——目标函数。 参考文献[7]的直接极小化指标函数的自适应优化算法,可得H的在线学习算法为 式中,QH(t)——Hessian矩阵。 QH(t)=QH(t-1)+ρ(t)· QH(t)求逆及克服算法病态的权重对角矩阵λe(t)的确定,可参见文献[8]的算法。 0.7sign[u(t-5)]u2(t-5), 式中,sign(·)——符号函数。 参考输入r(t)=(-1)^round(t/100),自适应滤波动态工作点u0(t)=0.9u(t-1),饱和限幅Umax=0.8。加权网络为 λ(q-1)=0.5-0.25q-1-0.24q-2。 H寻优时的目标函数的QH(0)=103.5I,采用Matlab7语言编程实现算法的仿真研究,结果如图1~3所示。 图1 不同模型的响应曲线Fig. 1 Response curve of diffevent model 图2 传统NARMA-L2模型的参数曲线Fig. 2 Parameter curve of original NARMA-L2 model 图3 改进NARMA-L2模型的参数曲线Fig. 3 Parameter curve of modified NARMA-L2 model (1)针对NARMA-L2模型存在的误差项值较大的问题,提出一自适应滤波动态工作点,在该工作点处由一阶泰勒展开逼近NARMA模型,建立了改进的NARMA-L2模型,其误差值较传统NARMA-L2模型小,其逼近NARMA模型的性能更优。 (2)利用多层BP神经网络能逼近任意非线性函数的性能,获得了BP神经网络辨识改进的NARMA-L2模型的参数。 (3)基于广义目标函数,根据改进的NARMA-L2模型,提出非线性系统的隐式自校正控制器算法,通过直接极小化指标函数的自适应优化算法寻优了BP神经网络的连接权重值,通过在线学习,给出了一种新的在线学习算法。2 神经网络自校正控制器
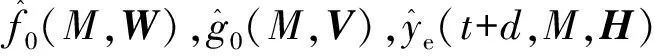


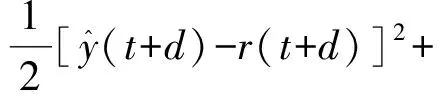
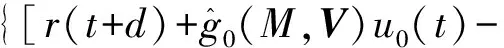
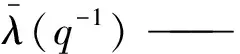
3 神经网络连接权重值的学习算法
3.1 梯度表达式
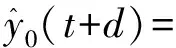
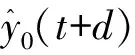
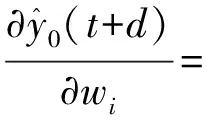
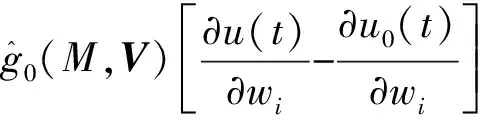
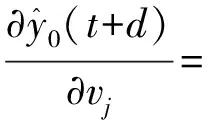
3.2 二阶导数矩阵
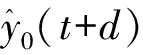

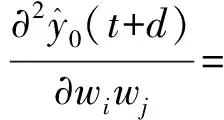


3.3 W、V的学习算法
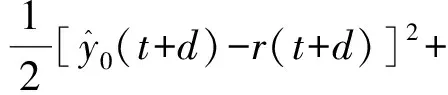
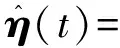
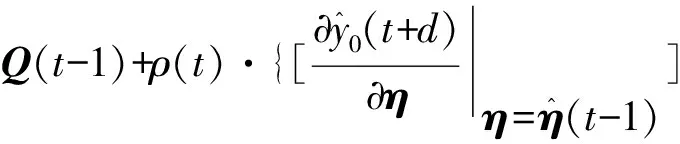

3.4 H的学习算法
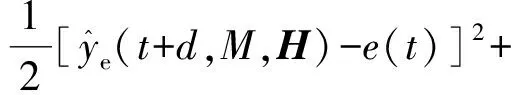
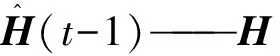
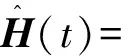
4 仿真研究
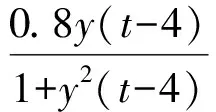

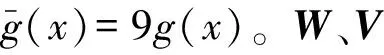

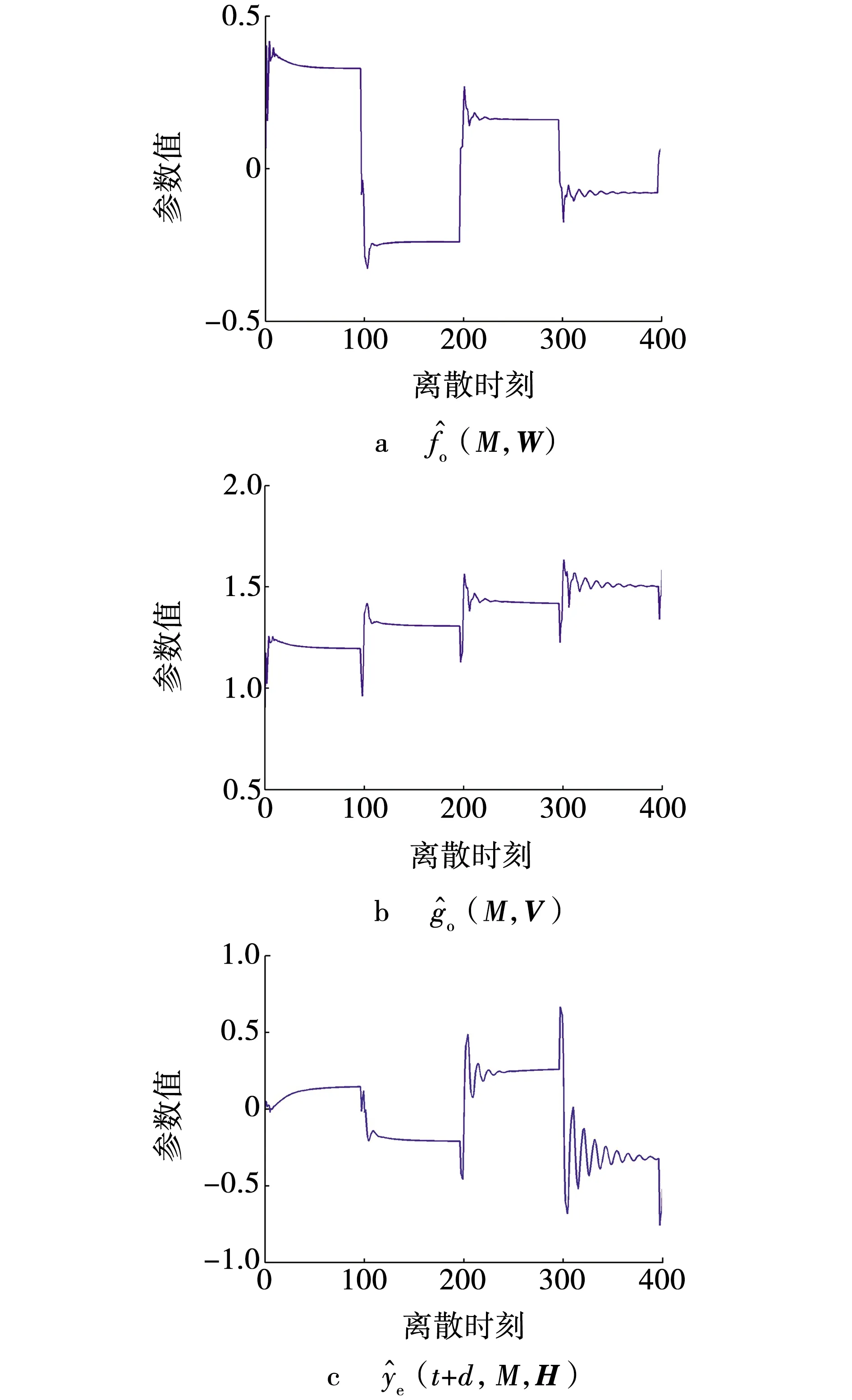
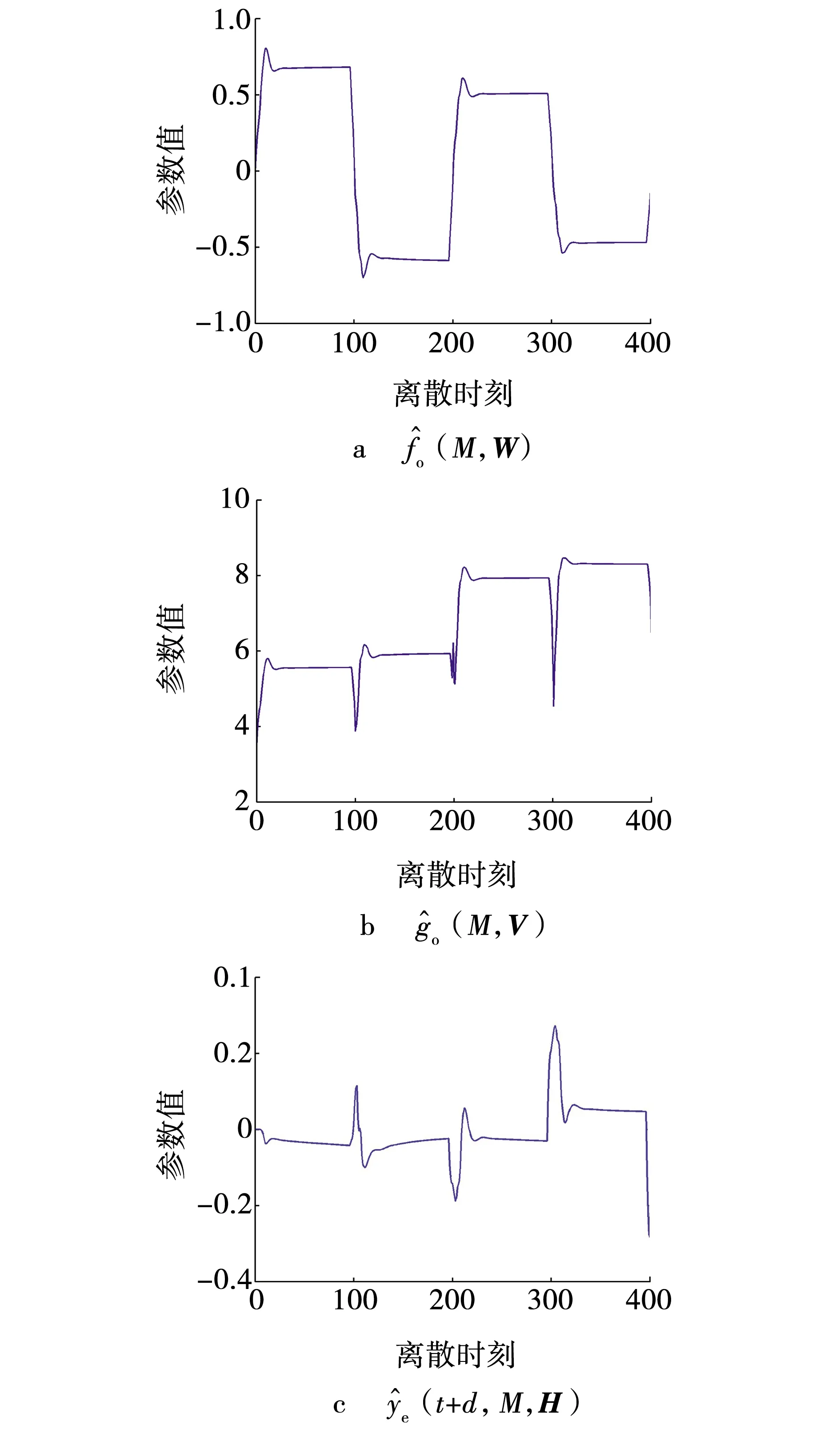
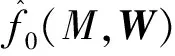
5 结 论
