觉知逻辑的个体信念更新
2021-12-09宋鹏飞熊卫
宋鹏飞 熊卫
1 引言
动态认知逻辑(Dynamic Epistemic Logic,[8])涉及两个主要的信息动态变化:公开宣告(Public Announcement)和个体信念更新(Private Belief Update)。信息的动态变化不仅会导致知识和信念的改变,也会导致觉知(Awareness)的改变。本文主要讨论个体信念更新1本文中,如果模型满足定义7,则该模型刻画了知识,此时的信念更新也是知识更新。及其相应的觉知变化,比如下面的例子:
例1.小张住在酒店,他知道酒店的餐厅有提供咖啡的服务,但是不确定餐厅今天是否提供咖啡。另外,小张对于餐厅有提供茶水的服务没有觉知。这时,小张听到有人说,今天餐厅不会同时提供咖啡和茶水。得知这个消息之后,小张虽然仍不知道餐厅今天是否提供咖啡和茶水,但是觉知到了餐厅有提供茶水的服务这件事。事实上,今天餐厅既不会提供咖啡,也不会提供茶水。令p为“餐厅今天提供咖啡”,q为“餐厅今天提供茶水”。小张的知识变化如图1 所示。
图1 是两个单主体模型。左边的模型表示小张得到信息之前的认知状态,其中只包含一个原子命题p,实心点是p为真的可能世界,空心点是p为假的可能世界,有下划线的可能世界是当前的可能世界,模型中的箭头表示主体的可通达关系,显然它是等价关系;右边的模型表示小张得到信息之后的认知状态,其中包含两个原子命题p和q,每个可能世界有两个点,左边的点表示p的真值,右边的点表示q的真值,实心为真,空心为假,与左侧模型一样,有下划线的可能世界为当前可能世界,箭头表示主体的可通达关系,它也是等价关系。
在模态逻辑中,不确定性可以通过命题在不同可能世界中的不同取值来刻画。对于某一主体在某一可能世界,如果一个命题在所有可通达的可能世界为真,则该主体相信(或知道)该命题为真。例1 描述了一个很简单的场景,图1 的可能世界模型刻画了该场景。但是,例1 与通过模态逻辑来刻画知识和信念的经典方法有所不同。在模态逻辑中,我们假设任一主体都能够觉知到所有相关的原子命题,这一假设被称为封闭世界假设(Closed World Assumption,[3]),而例1 中的主体得到信息导致模型增加了新的原子命题,显然,其不符合这一假设。因此,研究者尝试修改和完善克里普克模型,以支持主体对命题或公式有不同程度的觉知,以及主体的觉知发生变化。与此同时,在相应的逻辑语言中,也需要在认知逻辑中增加觉知算子以及导致觉知发生变化的动态算子。
形式刻画觉知的方案主要有两种:句法进路([9-11])和语义进路([13,14,21,22])。这两种方案的差异主要体现在哲学观点的不同。其中,句法进路认为,每一个可能世界都是客观的,所有的原子命题在任一可能世界都有取值;而语义进路则认为,可能世界是主观的,是存在于主体的思想中的,因此,那些没有被主体觉知到的原子命题就会在相应的可能世界上没有取值。具体而言,句法进路在可能世界语义中增加了觉知函数,使每一个主体在每一个可能世界对应一个公式集;而语义进路则是将克里普克语义结构扩展为所有主观可能世界构成的完全格。
由于上述两种方案都是在克里普克语义上加以扩展,因此,在处理个体信念更新的问题时,都会产生同样的问题,即,当某一主体接收到某一条信息,原本的认知模型需要被复制成两个副本,一个副本用来刻画接收到信息的主体的认知状态,另一个副本用来刻画未接收到信息的主体的认知状态。这样做的结果是,在一系列个体信念更新之后,认知模型会发生几何级数的增长。
由罗里尼(Lorini)提出的信念态度逻辑(Logic of Doxastic Attitude,[16,17])能够有效地规避上述问题。信念态度逻辑是以信念库(Belief Base,[12,20,23,24])为基础的逻辑,而信念库则是信念更新的AGM 方案([1])的重要概念。在信念态度逻辑中,对于个体信念更新,只需要改变该个体的信念库,而其他个体的信念库保持不变。由此,信念态度逻辑给出了个体信念更新的一种“节省的”方案,避免了复制模型导致的模型复杂度的几何级数增加。至此,有两种个体信念更新方式,即,通过改变信念库而实现的个体信念更新和通过复制模型而实现的个体信念更新,罗里尼([17])证明了这两种个体信念更新所产生的模型具有互模拟关系。但是,罗里尼的理论中并不包含觉知,因而不能涵盖前文提到的例子。对此,罗里尼等人在[18,19]提出了包含觉知算子的信念态度逻辑,并形成了与上述两种方案并列的第三种刻画觉知的方案——信念库进路(Belief Base Approach)。以此为基础,本文将在包含觉知算子的情况下证明上述两种信念更新产生的模型具有互模拟关系,并给出其成立的条件。另外,虽然[19]列出了该逻辑的个体信念更新扩充的公理,但并未证明这一扩充的可靠性和完全性。对此,本文将使用句法翻译的方法([8])证明该扩充相对于多主体信念库语义的可靠性和完全性。
本文的各部分内容安排:第2 节到第4 节是对[18]的回顾,在第2 节,我们定义了包含觉知的信念态度逻辑的逻辑语言;第3 节给出信念库语义模型的定义,进而规定不同的模型类;第4 节介绍了静态信念态度逻辑的公理系统以及该系统中不同的公理集合对于相应模型类的可靠性和完全性定理;从第5 节开始是本文的核心内容,在介绍了该逻辑在增加个体更新动态算子之后的扩充后([19]),我们用句法翻译的方法证明了该扩充对于信念库语义模型的可靠性和完全性;第6节将信念态度逻辑的个体信念更新与命题觉知逻辑的个体信念更新作比较,展现了前者在保持模型简洁性方面的优势,最后我们证明了这两种动态过程产生的模型具有互模拟关系;第7 节得出文章的结论并介绍后续工作。
2 逻辑语言
在这一节,我们回顾了包含觉知的信念态度逻辑LDAA(Logic of Doxastic Attitudes with Awareness,[18])的语言。令Atm{p,q,...}是可数无限的原子命题集,令Agt{1,...,n}是有限的主体集。LDAA 的语言由下面两层定义给出。首先是L0(Atm,Agt):

其中p ∈Atm,i ∈Agt。LLDAA(Atm,Agt)是在L0(Atm,Agt)的基础上增加隐信念算子得到的语言:

其中,α ∈L0(Atm,Agt),i ∈Agt。
当前后文明确时,可以将L0(Atm,Agt)简写为L0,将LLDAA(Atm,Agt)简写为LLDAA。其他布尔连接词∨,→,↔,⊤,⊥则是由¬和∧通过标准的方式定义。公式△iα读作“主体i显相信α为真”,公式○iα读作“主体i觉知到α”。算子△i可以被叠加,这说明LLDAA可以表达高阶信念,例如△i△jα,读作“主体i显相信主体j显相信α为真”。叠加可能是显信念算子和觉知算子的混合,例如△i ○jα,读作“主体i显相信主体j觉知到α”。
公式□iφ读作“主体i隐相信φ为真”。它的对偶♢i定义为:

♢iφ读作“φ与主体i的显信念有一致性”。
值得注意的是,模态词○i在逻辑语言的两层定义中都有出现,而模态词△i只出现在第一层。因此,觉知算子可以出现在显信念算子的辖域中,而隐信念算子不能出现在显信念算子的辖域中2这里对句法做出限制的原因是,在下一节的语义定义中,主体的信念可通达关系是由该主体的显信念计算出的,也就是说,隐信念是通过显信念来定义的。因此,如果隐信念算子出现在显信念算子的辖域中,将会产生循环定义的问题。规避这一问题方式是用“固定点”的方式来定义隐信念,而这会显著增加语义的复杂性。。另外,显信念算子和隐信念算子都能出现在觉知算子的辖域中。这是因为,本文研究的觉知是命题觉知,即关于原子命题的觉知,其含义是,主体觉知到某一公式等价于觉知到构成该公式的所有原子命题。令Atm(φ)表示出现在公式φ中的原子命题的集合,其递归定义如下:

令Γ⊆LLDAA是有限的公式集,定义Atm(Γ)∪
φ∈ΓAtm(φ)。
3 形式语义
这一部分回顾了包含觉知的信念库语义。([18])不同于克里普克语义的是,信念库语义中的可通达关系不是模型的初始条件,而是从信念库中计算得出的。这里首先给出“状态”的定义,它类似于克里普克语义中的可能世界。
定义1.一个状态是一个多元组S(B1,...,Bn,A1,...,An,V),其中,
•Bi ⊆L0是主体i的信念库,其中,i ∈Agt,
•AiAtm(Bi)是主体i的觉知集合,其中,i ∈Agt,
•V ⊆Atm是该状态中那些为真的原子命题集。
S 是所有状态的集合。下面的定义给出L0公式的语义解释。
定义2.对任意S(B1,...,Bn,A1,...,An,V)∈S:

定义3.包含觉知的多主体信念库语义模型MABA(Multi-agent Belief Model with Awareness)是一个二元组(S,Cxt),其中,S ∈S,Cxt ⊆S。
Cxt是所有主体的语境或共同背景(Common Ground,[25]),指的是所有主体共同分享的信息。从这些信息和各自的显信念中,主体能够做出推理。下面的定义规定了主体的信念可通达关系是由信念库计算出的。
定义4.对任意i ∈Agt,Ri是S 上的二元关系,其定义为:对任意S(B1,...,Bn,A1,...,An,V),S′

在定义了可通达关系的基础上,可以给出LLDAA公式的语义解释。其中,布尔公式与标准的定义保持一致,此处省略。
定义5.令(S,Cxt)是MABA,其中,S(B1,...,Bn,A1,...,An,V)。有如下等价关系:

下面两个定义给出了MABA 的属性,它们分别对应克里普克模型的自返性和持续性。
定义6.MABA(S,Cxt)满足全局可持续性GC(Global Consistency)当且仅当,对于所有i ∈Agt和所有S′ ∈({S}∪Cxt),存在S′′ ∈Cxt满足(S′,S′′)∈Ri。
定义7.MABA(S,Cxt)满足信念正确BC(Belief Correctness)当且仅当S ∈Cxt且对于所有i ∈Agt和所有S′ ∈Cxt,(S′,S′)∈Ri。
对于X⊆{GC,BC},MABAX是满足X 中的所有条件的MABA 模型类。MABA∅是所有MABA 模型构成的模型类,简记为MABA。很容易证明MABA{BC}MABA{GC,BC}。
令φ ∈LLDAA,φ对于MABAX模型类有效,当且仅当,对所有(S,Cxt)∈MABAX,(S,Cxt)|φ,简记为φ。φ对于MABAX模型类可满足,当且仅当,¬φ对于MABAX模型类不是有效的。
4 公理化
这一部分首先给出LDAA 逻辑对于不同模型类的公理集,然后介绍它们关于相应模型类的可靠性和完全性定理及证明思路。
基本的LDAA 逻辑是在经典命题逻辑的基础上增加以下公理和推理规则的扩充([18]):

对于X⊆令LDAAX是LDAA 逻辑增加下述公理的扩充:

对于逻辑LDAAX,X⊆,其中任意公式φ ∈LLDAA,用φ来表示φ是LDAAX的定理。对于LLDAA的公式集Γ,如果不存在公式φ1,...,φm ∈Γ满足(φ1∧...∧φm)→⊥,则Γ 与LDAAX一致。特别地,φ与LDAAX一致当且仅当{φ}与LDAAX一致。
接下来将介绍可靠性和完全性定理,由于其证明过程较长,这里只阐述[18]的证明思路。可靠性的证明比较简单,只需要验证每一个公理对于相应的模型类有效,每一个推理规则都能保持公式的有效性。对于完全性的证明,需要定义典范模型,而典范模型的定义需要克里普克语义结构,因此,需要给出LDAA 的两种类似克里普克结构的语义模型,它们被称为概念语义和准概念语义,在这两种语义中,可通达关系是模型的初始条件,然后只需证明信念库语义与这两种语义具有等价性。接下来只需要用典范模型的方法证明LDAAX对于具有相应性质的准概念模型具有完全性,即可得出完全性定理。
定理1.令X⊆。LDAAX对于模型类是可靠和完全的。([18])
证明.过程参见[18]的第三节和第四节。
5 LDAA 的个体信念更新
这一部分首先给出LDAA 在增加个体信念更新算子之后的扩充。([19])具体来说,在LLDAA(Atm,Agt)的基础上增加算子[+iα],可以得到语言LLDAA-PBE(Atm,Agt):

其中,i ∈Agt,α ∈L0,LDAA-PBE 读作“包含觉知与个体信念扩张的信念态度逻辑”,PBE 是Private Belief Expansion 的简写。
与第2 节类似,LLDAA-PBE(Atm,Agt)可被记作LLDAA-PBE。公式[+iα]φ读作“主体i的信念库增加α后,φ为真”。在定义5 的基础上增加如下可满足关系的定义,动态算子[+iα]可在MABA 中得到解释。
定义8.令(S,Cxt)是MABA,其中S(B1,...,Bn,A1,...,An,V)。有如下等价关系:

事件+iα只包含主体i得到信息α并将α增加到其信念库中,而其他主体的信念库保持不变。因为觉知集合是由信念库计算得出的,所以,在这一过程中,主体i的觉知集合间接地受到影响。
另外,个体信念更新不能保持模型的信念正确BC 或全局可持续性GC,因此,对个体信念更新的讨论是相对于所有MABA 构成的模型类MABA。
逻辑LDAA-PBE 在LDAA 的基础上增加如下公理和推理规则的扩充3注意到,LDAA-PBE 中并不包含个体更新算子叠加的公理,即对应定义9 第13 项的公理。其原因是,证明LDAA-PBE 的完全性并不是直接通过LDAA-PBE 的公理,而是利用定义9 的归约函数将所有LDAA-PBE 公式转化为LDAA 公式。LDAA-PBE 新增加的六条公理已经能够确保该归约函数可以将所有的LDAA-PBE 转化为LDAA公式。:

任意公式φ ∈LLDAA-PBE,用⊢LDAA-PBEφ来表示φ是LDAA-PBE 的定理。根据上述公理,可以给出归约函数redLDAA-PBE的递归定义,该函数将LLDAA-PBE的公式可以转化为等价的LLDAA公式。
定义9.函数redLDAA-PBE递归定义如下:


觉知的归约公式的意思是:通过将α增加到信念库中,主体i将出现在α的原子命题增加到他的觉知集合中;隐信念的归约公式的意思是,主体i在信念库中增加α后能够推出φ,当且仅当,在信念更新之前,主体i就能够推出α蕴涵φ;显信念的归约公式的意思是,主体i的信念库增加α,其他主体的信念库保持不变。
接下来,我们对[19]的内容做补充,证明LDAA-PBE 相对于MABA 的可靠性和完全性。在证明可靠性和完全性之前,需要首先说明上述归约函数redLDAA-PBE给出的等价式是LDAA-PBE 的定理,即,对于所有的φ ∈LLDAA-PBE,有⊢φ ↔redLDAA-PBE(φ)。这里存在一个问题,在做归纳证明时,通常需要将归纳假设应用在某一公式的所有子公式上,但是,对于包含个体信念更新算子的公式,这一方法是不够的。例如,¬[+iα]ψ并不是[+iα]¬ψ的子公式。因此,需要定义如下的公式复杂度函数,然后针对公式复杂度来提出归纳假设。
定义10.公式复杂度函数c:LLDAA-PBE→N 的定义如下:


公式复杂度函数c最后一项的参数2 并不是任意的,它是保证下面的不等式成立的最小自然数。
引理1.对于所有α,β ∈L0,以及所有φ,ψ,ψ1,ψ2∈LLDAA-PBE,

证明.只需要逐项验证这些不等式成立即可。
上述不等式说明被归约前的公式的复杂度大于归约得到的公式的复杂度4需要注意的是,引理1 省略了归约函数redLDAA-PBE 中那些不等关系显然成立的部分。。有了这一结果,我们可以对公式复杂度做数学归纳来证明下面的命题。
命题1.令φ ∈LLDAA-PBE。可以得到:

证明.对c(φ)做归纳:
当φ是原子命题p时,⊢LDAA-PBEp ↔p显然成立。
假设对于所有c(φ)≤n的φ,有⊢LDAA-PBEφ ↔redLDAA-PBE(φ),其中,n ∈N。
当φ的形式如¬ψ、ψ1∧ψ2、△iα、□iψ、○iψ时,结论可从归纳假设和引理1 的第一项得证。
当φ是[+iα]p时,结论可从公理AI、归纳假设、定义10 得证。
当φ是[+iα]¬φ时,结论可从公理PE&N、归纳假设、引理1 的第2 项得证。
当φ是[+iα](φ1∧φ2)时,结论可从公理PE&C、归纳假设、引理1 的第3项得证。
当φ是[+iα]□jφ时,其中ij,结论可从公理PE&IB、归纳假设、引理1 的第4 项得证。
当φ是[+iα]□iφ时,结论可从公理PE&IB、归纳假设、定义10 得证。
当φ是[+iα]△jβ时,结论可从公理PE&EB、归纳假设、定义10 得证。
当φ是[+iα]○jφ时,其中,ij或Atm(φ)⊆Atm,结论可从公理PE&A、归纳假设、定义10 得证。
当φ是[+iα]○jφ且并非是前一种情况时,结论可从公理PE&A、归纳假设、引理1 的第5 项得证。
当φ是[+iα][+jβ]φ时,由redLDAA-PBE的定义,可转化为上述情况。
下面的命题说明归约函数redLDAA-PBE确实可以将LLDAA-PBE公式转化为LLDAA公式。
命题2.令φ ∈LLDAA-PBE。则,redLDAA-PBE(φ)∈LLDAA。
证明.对c(φ)做归纳即可给出证明,此处省略具体步骤。
根据上述结果,我们可以证明LDAA-PBE 的可靠性和完全性定理。
定理2.LDAA-PBE 对于模型类MABA 是可靠和完全的。证明.对于可靠性,只需要验证每一个公理都是有效的,每一个推理规则都能在模型类MABA 保持有效性。因为LDAA 对于MABA 是可靠的,只需要验证新增的公理和推理规则,而其中大多数都是显然的,这里只证明公理PE&A 是有效的。当ij时,根据语义,[+iα]○jφ ↔○jφ显然成立。当Atm(φ)⊆Atm(α)时,根据语义,△iα →○iφ是重言式。由此可得,[+iα](△iα →○iφ)是重言式。由前面的等价式可知,后者等价于[+iα]△iα →[+iα]○iφ。因为[+iα]△iα ↔⊤,可以得到[+iα]○i φ ↔⊤。对于其他情况,由○iφ ↔∧p∈Atm(φ)Atm(α)○ip ∧∧p∈Atm(φ)∩Atm(α)○ip可以得到[+iα]○iφ ↔[+iα]∧p∈Atm(φ)Atm(α)○ip ∧[+iα]∧p∈Atm(φ)∩Atm(α)○ip。根据前一种情况,很容易得出[+iα]∧p∈Atm(φ)∩Atm(α)○ip ↔⊤。因此,有[+iα]○iφ ↔[+iα]∧p∈Atm(φ)Atm(α)○ip。因为p∈Atm(α),对p的觉知不受[+iα]事件的影响,可以得出,[+iα]○iφ ↔∧p∈Atm(φ)Atm(α)○ip。对于完全性,令|MABAφ。根据LDAA-PBE 的可靠性以及⊢LDAA-PBEφ ↔redLDAA-PBE(φ),可得|MABAredLDAA-PBE(φ)。因为redLDAA-PBE(φ)不包含任何动态算子,所以,由LDAA 的完全性可得,⊢LDAAredLDAA-PBE(φ)。由于LDAA 是LDAA-PBE的子系统,可以得到⊢LDAA-PBEredLDAA-PBE(φ)。根据命题1,有⊢LDAA-PBEφ。
6 LDAA-PBE 与命题觉知逻辑的个体信念更新
在这一部分,我们将针对个体信念更新的问题比较LDAA-PBE 与命题觉知逻辑LPA(Logic of Propositional Awareness),后者首先出现在[10],是一般觉知逻辑LGA(Logic of General Awareness,[9])的特殊情况。
LPA 的语言LLPA(Atm,Agt)由下面的语法给出:

其中,p ∈Atm,i ∈Agt。公式Biφ读作“主体i隐相信φ为真”,公式Aiφ读作“主体i觉知到φ”,公式Xiφ读作“主体i显相信φ为真”。与前文一致,其他布尔连接词∨,→,↔,⊤,⊥由¬和∧通过标准的方式定义,LLPA(Atm,Agt)简写为LLPA。在语义层面,只需要将LGA 的语义模型的觉知函数的取值设定为原子命题集的幂集,就可以得到LPA 的语义模型。
定义11.命题觉知模型PAM(Propositional Awareness Model)是一个四元组M(Ω,⇒,ρ,π),其中,
• Ω 是非空的可能世界集,
•⇒:Agt×Ω−→2Ω是信念可通达函数,
•ρ:Agt×Ω−→2Atm是命题觉知函数,
•π:Atm −→2Ω是赋值函数。
PAM 是所有PAM 构成的集合。对于PAMM(Ω,⇒,ρ,π)及s ∈Ω,二元组(M,s)被称为PAM 的点模型。t ∈⇒(i,s)可记作s ⇒i t。下面给出LLPA的公式相对于PAM 的点模型的语义解释。
定义12.给定PAMM(Ω,⇒,ρ,π)及可能世界s ∈Ω,对于LLPA的公式,有如下等价关系:

对比LPA 和LDAA 的定义,可以看出这两种逻辑是基于不同的哲学出发点。在LPA 的语义中,主体的信念可通达关系和觉知集合都是模型的初始条件,而主体的显信念是由这两个条件计算得出的;而在LDAA 的语义中,模型唯一的初始条件是主体的显信念,而隐信念和觉知都是由显信念计算得出的。由此可见,LDAA减少了理论的前提假设,更符合奥卡姆剃刀的原则。另外,这两种逻辑刻画了不同意义的显信念概念。在下面给出的翻译函数中也能看出这种差异,LPA 的显信念并没有直接对应LDAA 的显信念,而是对应LDAA 的隐信念和觉知的合取。实际上,LDAA 的显信念表示当前活跃在主体认知中的信念,即工作记忆中的信念(主体的信念库即该主体的工作记忆);而LPA 的显信念表示,在主体觉知到的原子命题构成的信念中,该主体相信为真的那些信念,这样的信念并不一定处在工作记忆中,但是能被主体所理解。值得重视的是,[18]建立了由LPA 到LDAA 的多项式嵌入,这说明后者以更少的前提假设提供了更强的表达力。
接下来,为了证明互模拟定理,需要定义LLPA和LLDAA之间的翻译函数:

需要注意的是tr←并不是tr的反函数,因为需要在tr←中给出△i算子的翻译,而tr不会涉及到△i算子。实际上,tr←是一个偏函数,其自变量如果是显信念的否定式,它的函数值为空。这样做的原因是,如果将LDAA 的显信念的否定直接翻译成LPA 的显信念否定,有可能会产生矛盾。根据[17],LDAA 的显信念表示主体的工作记忆,所以有可能α不在主体i的工作记忆中,但□iα ∧○iα为真。
以PAM 为基础,范·迪特玛希(van Ditmarsch)等人刻画了信念和命题觉知的动态变化([3-5,7]),其中,个体层面的动态在[5]得到研究,其方法是使用行动模型([2,15])。它存在的问题是,在一系列个体信念更新的操作之后,通过与行动模型做乘积计算得出的PAM 会呈现几何级数增长。为解决这一问题,在罗里尼提出的信念态度逻辑中([17]),初始的信念库模型经过一系列个体信念更新之后,其数量级只会发生相对于信念更新次数的线性增长。然而,罗里尼只给出了以信念库语义模型为基础的个体信念更新过程,且不包含觉知。为应对这一问题,接下来,我们将以PAM 作为初始模型得出互模拟的结论,其中同时包含觉知的变化。
[18]的第3 节给出了LDAA 的三种语义对于一个有限公式集成立,而将PAM转换为MABA 也需要利用这个语义等价性的结论,因此,这里我们也只考虑LLDAA的有限公式集。
信念库模型的个体信念更新
令M(Ω,⇒,ρ,π)是PAM(Ω 有可能是无限集),Σ⊆LLPA是对子公式封闭的公式集,tr(Σ){tr(φ):φ ∈Σ}。为了证明的方便,令Σ′Σ∪{Aip:p ∈Σ,i ∈Agt}。很显然,tr(Σ′)⊆LLDAA是一个有限集,且对子公式封闭。
根据[18] 的定理3 和第3 节的语义等价性证明,可以找到一个有限集Cxt和一个满射σ:Ω→Cxt满足,对每一个s ∈Ω,如果σ(s)S,其中S(B1,...,Bn,A1,...,An,V),那么,
• 对每一个p ∈Σ′:tr(p)∈V当且仅当s ∈π(p),
• 对每一个Bi和每一个p ∈Σ′:tr(p)∈Atm(Bi)当且仅当p ∈ρ(i,s)∩Σ′5这一项解释了为什么我们令Σ′包括{Aip : p ∈Σ,i ∈Agt}。如果不这样做,对模型的过滤就不能保证主体i 在某一信念库的觉知集合与Σ 和主体i 在PAM 的相应可能世界的觉知集合的交集相等。为了证明互模拟关系,需要保证觉知集合在Σ 的限定内是不变的。,
• 对每一个Ai:AiAtm(Bi),
• 对每一个t ∈Ω:如果s ⇒i t,那么(S,σ(t))∈Ri,
• 对每一个S′ ∈Cxt:如果(S,S′)∈Ri,那么存在t ∈⇒(i,s)满足S′σ(t)。
很容易验证,对于每一个S ∈Cxt,(S,Cxt)是MABA,对每一个φ ∈Σ′和每一个s ∈Ω,(M,s)当且仅当(σ(s),Cxt)(φ)。
接下来对(S,Cxt)应用个体信念更新。假设主体i的信念库增加了α,其中,α ∈L0(Atm(tr(Σ′),Agt),tr←(△iα)∈Σ′。然后,根据定义8,可以得到(S+iα,Cxt)。
为了证明互模拟关系,需要将(S+iα,Cxt)翻译回PAMM′(Ω′,⇒′,ρ′,π′):

• 对每一个i ∈Agt和每一个sS′ ∈Ω′:

• 对每一个i ∈Agt和每一个sS′ ∈Ω′:ρ′(i,sS′)A′,
• 对每一个p ∈Atm(Σ′):π′(p){sS′ ∈Ω′:p ∈V ′}。
PAM 的个体信念更新
与前一部分相类似,我们用过滤的方法将M(Ω,⇒,ρ,π) 转换成有限的PAMMΣ′(ΩΣ′,⇒Σ′,ρΣ′,πΣ′)。由库伊和雷恩(Kooi&Renne,[15])提出的箭头更新模型(Arrow Update Model),这里定义该模型相对于PAM 的形式。
定义13.一个箭头更新模型是一个三元组U{O,τ,A},其中,
• O 是非空的输出集,其中每一个元素被称为一个输出,
•τ:Agt×O×O→LLPA×LLPA是一个偏函数,
•A:Agt×O→2Atm是觉知变化函数。
为了表达上的方便,对每一个i ∈Agt和每一个o′,o′′ ∈O,如果τ(i,o′,o′′)(φ,ψ),用τ1(i,o′,o′′)来表示φ,用τ2(i,o′,o′′)来表示ψ。
箭头更新模型(U,o)作用于PAM 点模型(M,s)之后,产生一个新的PAM 点模型,我们称之为乘积模型。下面是乘积模型的定义。
定义14.令(U,o)是一个箭头更新模型,其中,U{O,τ,A}。令(M,s)是一个PAM 点模型,其中,M(Ω,⇒,ρ,π)。(U,o)作用于(M,s)产生的乘积模型是(M ⊗U,(s,o)),其中,M ⊗U(Ω′,⇒′,ρ′,π′):

箭头更新模型以|O|为倍数增大了初始模型。具体来说,对每一个输出o′ ∈O和PAM 的每一个可能世界s′,会产生s′的一个增加了下标o′的复制(s′,o′)。而且,对每一个i ∈Agt和每一个输出对(o′,o′′),箭头更新模型指定了起始条件τ1(i,o′,o′′)和目标条件τ2(i,o′,o′′),它们分别被s′和s′′满足,进而保证在乘积模型中,(s′,o′)和(s′′,o′′)具有i-可通达关系。这样规定使得,可通达关系在乘积模型中被保留的充分必要条件为相应的两个初始可能世界对应于该输出分别满足起始条件和目标条件。A函数的功能是扩大主体的觉知集合。具体来说,它将每一个主体和每一个输出对应一个原子命题集,在乘积模型中,这一原子命题集将是该主体在被该输出下标的可能世界的觉知集合的子集。直观上讲,这意味着在乘积模型中,主体的觉知集合因为增加了一些原子命题作为元素而被扩大。
为了刻画在其他主体的信念不变的情况下某一主体的信念更新,需要定义一个特殊的箭头更新模型——个体箭头更新模型(Private Arrow Update Model)。它只包含两个输出:o1和o2。对于输出o1,他的觉知集合在每一个可能世界都会扩大,而在φ为真的可能世界,主体i减少他的可通达世界;对于输出o2,没有任何事发生。
定义15.对于主体i、公式φ、觉知扩张集合AE ⊆Atm,其中Atm(φ)⊆AE,相应的个体更新模型是U(φ,AE)i(O,τ,A),定义如下:
• 对于每一个k,h ∈{1,2}和每一个j ∈Agt,τ(j,ok,oh) 有定义当且仅当(k1 且h2)或kh2,
•τ(i,o1,o2)(⊤,φ)且τ(i,o2,o2)(⊤,⊤),
• 对所有ji,τ(j,o1,o2)(⊤,⊤)且τ(j,o2,o2)(⊤,⊤),
• 如果ij且k1,A(j,ok)AE,
否则,A(j,ok)∅。
令U(tr←(α),Atm(α))i(O,τ,A) 是对于主体i、公式tr←(α)、觉知扩张集合Atm(α)的个体箭头更新模型。给定PAM 点模型(M,s),其中M(Ω,⇒,ρ,π),M ⊗U(tr←(α),Atm(α))i,(s,o1))是(M,s)和(U(tr←(α),Atm(α))i,o1)的乘积模型。具体来说,PAMM ⊗U(tr←(α),Atm(α))i(Ω′,⇒′,ρ′,π′)的定义如下:
• Ω′{(s′,o1):s′ ∈Ω}∪{(s′,o2):s′ ∈Ω},
• 对所有s′ ∈Ω 和所有j ∈Agt:

• 对所有p ∈Atm:
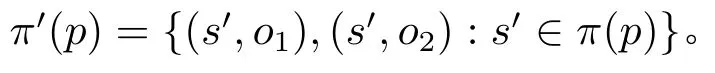
在下文中,将(M ⊗U(tr←(α),Atm(α))i,(s,o1))记作(M,s)(tr←(α),Atm(α))i。
互模拟
接下来我们证明两种个体信念更新产生的模型具有互模拟关系。在此之前,有两点需要注意。第一,互模拟关系应该局限在原子命题集的一个有限子集内;第二,与标准的克里普克模型的互模拟不同,这里的互模拟关系应该将模型中的觉知函数考虑在内。范·迪特玛希等人提供了包含觉知的互模拟定义([6]),在他们的文章中,这一互模拟被称为标准互模拟。
定义16.令Q⊆Atm,给定两个PAMM(Ω,⇒,ρ,π)和M′(Ω′,⇒′,ρ′,π′),这两个模型的Q 标准互模拟是关系R(Q)⊆Ω×Ω′满足,对每一个(s,s′)∈R(Q),每一个i ∈Agt,和每一个p ∈Q:
• 原子命题:s ∈π(p)当且仅当s′ ∈π′(p),
• 觉知:Q∩ρ(i,s)Q∩ρ′(i,s′),
• 正向条件:如果s ⇒i t,那么存在t′ ∈⇒′(i,s′)满足(t,t′)∈R(Q),
• 反向条件:如果s′ ⇒i t′,那么存在t ∈⇒(i,s)满足(t,t′)∈R(Q)。
对于两个PAM 点模型(M,s)和(M′,s′),其中M(Ω,⇒,ρ,π),M′(Ω′,⇒′,ρ′,π′),如果存在互模拟关系R(Q),且(s,s′)∈R(Q),则这两个点模型有Q 互模拟关系,记做(M,s)Q(M′,s′)。
根据[6]的命题21,可以得到,如果(M,s)Q(M′,s′),那么(M,s)和(M′,s′)满足LLPA(Q,Agt)中的相同的公式。
下面的定理是这一部分的核心结论,这一互模拟关系的左右两边各是一个PAM 点模型,其中,左边的模型是通过信念库语义的个体信念更新得到的,右边的模型是通过个体箭头更新模型得到的。
定理3.(M′,sS+iα)Atm(Σ)(MΣ′,[s]Σ′)(tr←(α),Atm(α))i
证明.令M′(Ω′,⇒′,ρ′,π′),将M ⊗U(tr←(α),Atm(α))i记做M′′,令M′′(Ω′′,⇒′′,ρ′′,π′′),令初始PAMM(Ω,⇒,ρ,π)。很容易得到:

定义二元关系R(Atm(Σ))⊆Ω′×Ω′′如下:

用常规的方式就可以验证R(Atm(Σ)) 定义了M′和M′′的标准互模拟关系,因此,具有互模拟关系。
值得注意的是,定理3 的成立需要满足四个条件:第一,具有互模拟关系的两个模型都是有限模型,因此,需要将初始模型用对子公式封闭的公式集来过滤得到有限模型;第二,过滤时,对子公式封闭的公式集Σ 需要转化为Σ′,从而包括所有主体对Σ 的原子命题的觉知命题;第三,如果α是主体i的信念库中增加的公式,那么,tr←(△iα)是Σ′中的公式;最后,α是L0公式。
在证明过程中,定理3 与[17]的定理11 使用的方法有一些相同点和不同点。相同点是,在模型的动态变化过程中,两者都使用了信念库的更新和个体箭头更新模型。不同点是,前者以PAM 作为证明的起始模型,而后者以信念库语义模型作为证明的起始模型,基于[18]的由LPA 到LDAA 的多项式嵌入,以PAM 作为证明的起始模型允许我们将LDAA 的技术直接应用在LPA 上;由于证明的起始模型的不同,两者在证明过程中需要对模型做不同的处理,前者需要将模型过滤以得到有限模型,进而通过[18]的模型转化方法得到MABA,而后者则是将所有显信念公式作为原子命题来处理,进而从信念库语义模型得到克里普克模型;最重要的是,相比于后者,前者的模型中包含觉知,因此,定义14 给出的个体箭头更新模型的最后一项是对主体觉知的更新,定义16 提出了互模拟需要满足觉知相等的条件。
更进一步,定理3 为LDAA 和LPA 的语义在技术方面和哲学方面的差异提供了很好的说明。技术方面,在LPA 的语义模型PAM 中,需要通过主体的信念可通达关系来确认该主体的隐信念,而显信念又是通过隐信念和觉知计算出的,因此,主体的个体信念更新意味着需要为每一个这样的主体复制整个模型;反观LDAA的语义模型MABA,每个主体的信念库都是相互独立的,认知模型是从主体的信念库构造出来的,这意味着,当某一主体的显信念发生变化时,认知模型也会自动发生变化。哲学方面,对于PAM,隐信念和觉知都是模型的初始条件,因此,为实现主体显信念的更新,需要同时改变主体的隐信念和觉知;而MABA 与之不同,我们只需要更新主体信念库中的公式集即可实现该主体的显信念更新。

图2:图表展示了以PAM 为初始模型的两种个体信念更新方案的关系。其中,PBE 指信念库的个体信念更新,PAU 指个体箭头更新。
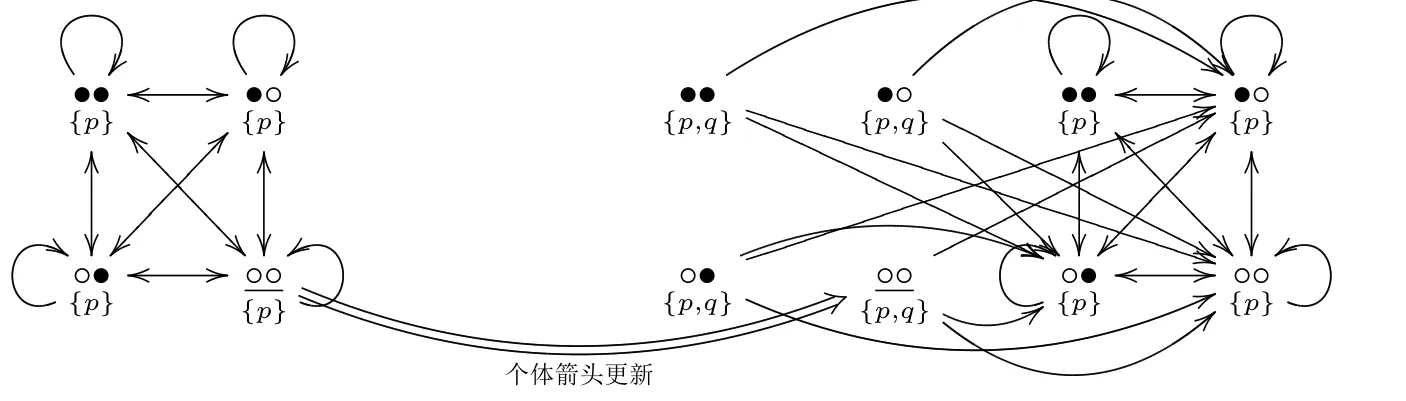
图3:这是用个体箭头更新过程来展示例1 的模型变化过程。图中有两个单主体模型。左边的模型是信念更新之前小张的认知状态,右边的模型信念更新之后的认知状态。大括号中的原子命题表示小张在该可能世界的觉知集合,模型中其他元素的解释与图1 保持一致。

图4:这是用信念库语义模型的个体信念更新过程来展示例1 的模型变化过程。大括号中的公式表示小张信念库中的公式,图中的其他元素的含义与图1 保持一致。
图2 展示了这一节的完整过程。通过本节我们证明了,尽管LPA 的显信念算子Xi被翻译成LDAA 的□i和○i算子,针对△i算子的个体信念更新仍然可以用在基于PAM 的动态变化中。回到文章开头提出的例子,图3 和图4 分别展示了这两种信念更新的模型变化过程。很容易看出,基于信念库语义模型的个体信念更新大大简化了模型的转化过程,避免了模型的复制。
7 结论与后续工作
本文证明了以信念库语义为基础的个体信念更新的动态逻辑LDAA-PBE 相对于多主体信念库语义的可靠性和完全性。同时,本文将两种个体信念更新方案做比较,它们分别是:基于信念库语义的个体信念更新、基于克里普克语义的个体箭头更新。通过模型转换的方法,我们证明了这两种方案形成的模型具有互模拟关系。其中,前一种方案只会使模型的规模发生线性增加,而后一种方案在每次个体信念更新时都必须复制模型,从而在一系列更新之后会使模型规模产生几何级数增加。这说明前一种方案在达到相同目的的同时,能够有效保持模型的简洁性。
在后续工作中,我们不仅会考虑对原子命题的觉知,也会研究某一主体对其他主体的觉知,尝试以信念库语义为基础建立关于身份的觉知逻辑,而关于这一觉知的动态变化也会纳入该逻辑的讨论范围。
