指向核心素养的初中数学实验活动

王金水 张洁 林晴岚

摘  要：以旗杆、金字塔等实物测量为实验目标，让学生通过“做”数学、“学”数学、“用”数学，经历数学抽象、推理论证等过程，使学生身心互为一体、知行相互作用，逐步形成综合能力，促进数学学科核心素养的生成.

关键词：相似三角形;数学实验;实践活动;核心素养

数学起源于现实，需要从做中学，才能真正感受知识的内涵. 而当前学生获取知识常常是纯粹将前人总结的经验加以消化和传承，重结果、轻过程，少有亲自动手实践. 这显然忽略了个体对知识的理解和情感体验，难以实现全面、持续、和谐的发展. 要改变知识单向传授的局面，实现从接受式学习向发现式学习的转型，需要搭建个体与知识之间双向沟通的实验桥梁.

数学实验活动是在特定环境下，对具有一定数学意义的实物、模型等，进行观察、计算、推理、验证等，探求某类数学问题，获得感性认识和数学信息的活动. 数学实验串起了数学思想、数学方法和数学知识，实现了过程与结果、操作与思维、证伪与证实的有机融合，是一种再发现、再生长的过程，是发展的源泉和动力. 数学实验可以满足不同学生的需求，既重视学生外在的操作活动，也重视其内在的心理活动，是数学学科核心素养落地生根的重要途径. 笔者以“相似三角形的运用”为载体，通过让学生借助实物等测量工具，启思明理、手脑并用，使学生身心互为一体、知行相互作用.

一、实验目的

以测量具体物高为实验对象，借用生活中的现象，从经验中学习，设计实验方案，挖掘隐藏在知识中的数学思想方法. 在“做”中让学生动手又动脑，培养有序操作的实践能力，学会合作交流，形成良好的团队精神;在“学”中清晰数学思维和实践应用，关注“同一地点、不同时刻的两个物体的影长所成比例”的研究，培养学生多角度观察、直观想象、有序思考、严谨表达与概括等思维活动能力;在“用”中发展学生的学习潜能，重视学生学习经验的获得，实现静态数学观与动态数学观的融通，提升解决问题的能力和创新思维能力，让数学教学更加具有活力.

二、实验内容

显性方面是通过动手操作（计算、演示等）、动脑思维（建模、推理等），将实际物体的测量问题抽象成数学模型，掌握测量方法，验证“同一地点，两物体不同时刻影长比相同”及解决影长不在同一平面上求物体高度等问题.

隐性方面是让学生形成一定的能力与品质，学会学习、爱上学习，具备综合实践的能力，具备终身学习的能力.

三、实验流程

实验基本流程：探究—引导—发现.

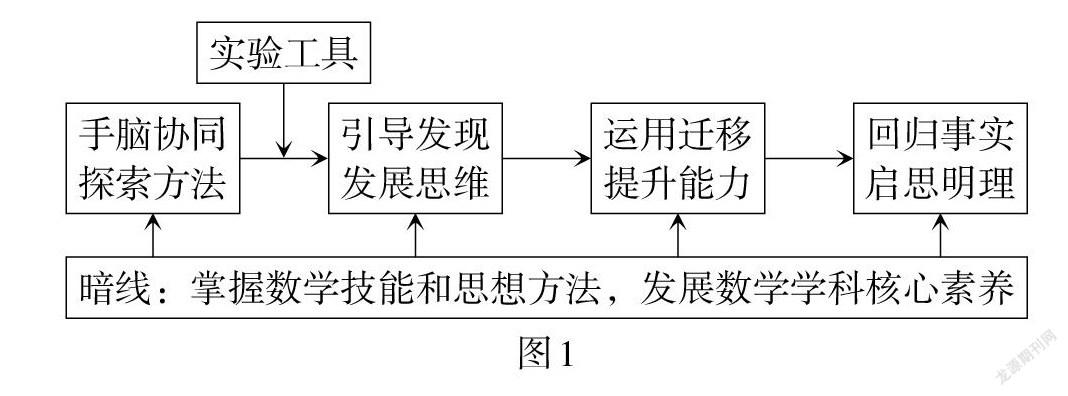
纵（明）线：手脑协同，探索方法;引导发现，发展思维;运用迁移，提升能力;回归事实，启思明理. 在探索方法中让学生捕捉實验背景，实现与实验目标产生直接而必然的联系;在引导发现中让问题有层次，从静止到变化、从单一到复杂，与背后的数学原理产生内在联系;在运用迁移中实现知识迁移与整合;在回归事实中学会用数学眼光看待事物，启思明理，凸显实践性思维，积累数学基本活动经验.

横（暗）线：学生在获取知识经验的同时掌握数学技能和思想方法，形成理性思考论证习惯，发展数学学科核心素养.

实验路线图如图1所示.

四、实验过程

以小组为单位，合作交流，从“做”数学到“学”数学再到“用”数学，让测量便于操作，过程更加灵活，结论可以测试.

1. 手脑协同，探索方法

“做”数学. 以问题为载体，将数学实验教学引入课堂，为学生提供参与学习过程的机会，把现实问题数学化，充分发挥个体的想象力和思维力，从而获得较为准确的数学感性认识.

环节1：旗杆测量问题.

课前通过实地考察，让学生思考和设计旗杆测量问题，小组交流展示.

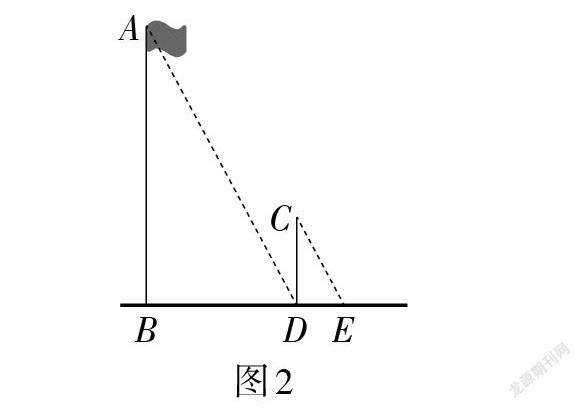
组长1：采用影长测量法. 具体操作为：如图2，CD表示生1的身高1.6米，AB表示直立的旗杆，测出同一时刻AB的影长BD的值和CD的影长DE的值.

影长测量法直观简单. 通过让学生测量自己的影长等，激发兴趣、诱发思考、产生联想，建立一定的数学直观或直觉，使得数学学习不再枯燥.

组长2：采用标杆测量法. 具体操作为：如图3，CD表示生2的身高1.7米，AB表示旗杆，EF为一根2米长的标杆，且直立在旗杆与生2之间. 当生2的眼睛（点C）、标杆的顶端（点E）、旗杆的顶端（点A）恰好在同一直线上时，其他同学测量出DF及BF的长即可.

标杆测量法需要借助实验工具. 三点成一线是测量的难点，要不断调整标杆或测量者的位置，学生在现场亲身感受、体验、交流、辨析等，可以积累更多的经验，生成更多的智慧.

组长3：采用镜中倒影法. 具体操作为：如图4，在身高1.7米的生3（CD）与旗杆（AB）之间的地面上平放一面镜子（点E），当生3能够通过镜子（点E）看到旗杆顶端（点A）时，其他同学测得DE与BE的长即可.

镜中倒影法是利用光的反射原理. 图4中CD的长是指眼睛与地面间的距离. 借助观察镜面的反射调动自己的感官，不同人测量旗杆的高度值也许不同，在合理的范围内，感受数学事实，满足学生自我展示的愿望，有利于学生的终身发展.

师：说一说这些测量方法的可行性及其特点.

生4：影长测量法需要影子，有阳光是前提;标杆测量法不用影子，但标杆与旗杆的顶端必须看得见. 镜中倒影法不用影子，但镜面（水面）必须水平，测量的环境一定是在水平地面上.

测量调动了学生的感官，通过对信息的加工、转换和思考，把操作与思维结合起来，以夯实基础、激发潜能、提升技能. 不难看出，每个测量结论的产生都伴随着一段严谨的实验过程，使学生聚焦不同方法、比较不同算法、挖掘共同本质、掌握数学建模等基本方法和技能，达成知识的发展性价值及学生思维培养的目标.

2. 引导发现，发展思维

实验是挖掘知识的本源性问题、还原“学”数学的过程. 在学习、探索、发现、探讨规律性结果的实验中，通过感悟知识的抽象过程、传递人类积累的经验、发现已知或潜在的数学事实，实现研究内容的可视化，从而促进学生个体空间想象力、推理能力和论证能力的提升.

环节2：测量胡夫金字塔的高度.

介绍胡夫金字塔的测量典故，建立与旗杆测量相互联系的实践机会. 胡夫金字塔塔基呈正方形，边长约230米，千年来无人知其高度. 泰勒斯利用某时刻自己的影长等于身长推导塔影等于塔高的原理，从而测量出了胡夫金字塔的高度.

题目  如图5，若泰勒斯（CA）身高2米，他的影长AD为3米，测得胡夫金字塔的影长OA为201米，求胡夫金字塔的高度BO.

问题简单，多数学生采用影长测量法，利用△AOB ∽ △DAC，有[BOOA=CAAD.] 求得BO = 134（米）.

问题：题目中的三个已知数据是否可信？

生：实际测量当然可信.

追问：OA是怎么量的？

追问的目的在于改变知识维度，转换问题方向. 很明显，学生都认为是点A到正方形的距离加正方形边长的一半，展现了数学逻辑的魅力及数学思考的经验.

生5：若塔基无规则（非标准正方形），则OA无法直接测量，该怎么办？

问得很好，一石激起千层浪. 此时展现的问题具有独特的价值，推进实验向纵深发展. 除了金字塔影长为0的特殊时刻外，学生都一时难以找到影长的测量方法.

生6：影长会随着时间的变化而变化，那么影长的增加量与时间的增加量有什么关系？

生6的疑问给大家指明了研究方向，激发了学生的思维灵感，学生想到借助两次或两次以上的影长变化来研究问题，一致认为胡夫金字塔的影长与泰勒斯的影长变化规律相同，只要研究泰勒斯的影长变化规律就可以了. 此时，多数学生认为影长的增加量与时间的增加量成正比. 这一“创造性”想法马上遭到另外一部分学生的反驳，因为中午时刻影长变化率不大，而太阳下山时，影长变化率非常大. 去伪存真、去虚求实，这需要反思性、批判性、创新性思维的参与，在“证伪”“证实”间，学生更有了远见和思想.

生7：我认为，不同时刻，同一地点，不同的两个物体的影长之比可能相等.

简而言之，同一地点，不同物体在不同时刻下对应的影长成比例. 生7这一观点，似乎有道理，如何验证呢？可信的结论，必须给出严谨、科学的理论证明. 笔者引导学生以此结论为实验对象，以小组为单位，分组参与不同的实验环节，各自利用实验工具或几何画板软件干预变量，收集数据，让思维可视化.

生8：如圖6，线段AB，CD分别代表泰勒斯和他的助手. BE，BM，DF，DN分别代表不同时刻他们的影长. 根据同一时刻太阳光是平行的，有AE∥CF，AM∥CN，进而得△ABE ∽ △CDF，△ABM ∽ △CDN. 所以[ABCD=][BEDF， ABCD=BMDN.] 所以[BEDF=BMDN.]

笔者用红笔圈出生8所列比例式[BEDF=BMDN，] 引发学生有目的地思考，聚焦问题的核心，促进操作向正确的方向发展，并要求生8用语言叙述自己的发现.

生8：同一地点，不同时刻两个物体的影长成比例.

师：归纳得非常正确. 但金字塔的两次影长都是未知的，怎么办？

生9：它们之间有联系，可以用方程思想解决.

生10：如图7，只要泰勒斯从原位置A处沿着影长AD再走到点D处，则在某一时刻金字塔的影长末端刚好在点D处时，再测出泰勒斯的影长DF的长，就有办法测出金字塔起始影长OA.

师：为什么？

生10：由AC = DE，设OA = x. 根据同一地点，不同时刻的两个物体的影长成比例，有[ADOA=DFOD.] OD = OA + AD，AD与DF可测，则可以求出OA的值.

在思维的碰撞中擦出新的火花，发现了不同物体、不同时刻下的两次影长比相同，破解了底部无法到达的测量问题. 学生们感到无比兴奋，人人焕发全新的活力，在相互启迪、鼓励中，感受到发现的乐趣，满足学生创造性学习的要求，构建了合理的知识体系，促进了学生学习能力的整体提升.

生11：按照这一结论，生10的论述就不具有一般性了. 在图5的基础上，如图8，只要泰勒斯从点A沿着影长AD（已测）再走到任意点H处，当在某一时刻金字塔的影长末端刚好在点H时，测出泰勒斯的影长HF的长及其所走路程AH的长，根据[ADOA=HFOH，] OD = OA + AD，OH = OA + AH，AD和AH均可以测量，就有办法测量起始影长OA的长.

对金字塔的空间想象和数据测量与运算，从直接测量到间接测量，引发学生逐步深入，手脑并用协同促进，体验数学的发现过程，即从“猜想—数学化的表达—形式化的证明—概括迁移—创造思维”，实现了问题的简单化，理清了数学知识的发展始末. 实验是不断发现知识、理解知识和应用知识的过程. 实践中得到的知识技能、创造能力和科学研究意识，极大促进了学生数学抽象、数学建模、数学运算等关键能力的生成，尤其是养成了坚韧不拔的品质，进而推动学生的全面发展.

3. 运用迁移，提升能力

加强和塑造“用”数学，积累数学经验学会学以致用，促进对数学事实的认识，形成具有连续性和生长性的经验，让数学知识得到迁移和理解，增强学生适应社会的能力.

环节3：真实背景下测量树木的高度.

观察校园树木的周围环境. 要求学生从中发现问题，自主提出问题，再与全班学生一起尝试抽象构图、数学思考、模型建构，找到问题解决的方案.

生12：如图9，测得长为1米的竹竿的影长为0.8米，甲树的影长为4.8米，甲树多高？

简单应用，营造轻松、自然或自发的学习氛围，感受到共同探究的乐趣和成就感.

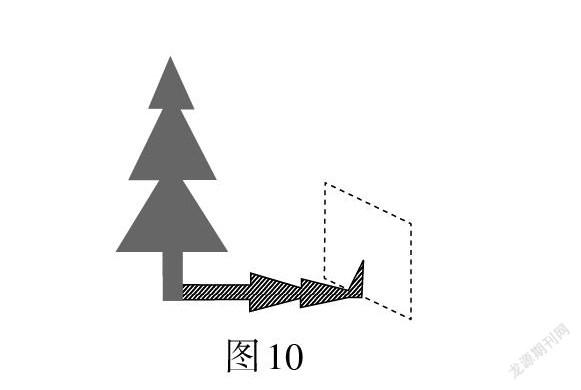
生13：如图10，测得长为1米的竹竿的影长为0.8米，发现乙树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上，墙壁上的影长为1.2米，落在地面上的影长为2.4米，乙树多高？

树木周围环境有变，面对数学事实，发展抽象思维，激发学习兴趣.

生14：如图11，测得长为1米的竹竿的影长为0.8米，发现丙树影子除落在地面上外，还有一部分落在教学楼的第一级台阶上，测得此影子长为0.2米，一级台阶高为0.3米，落在地面上的影长为4.6米，丙树多高？

周围环境再变，影长落在了三个平面内，让知识结构不断发展.

生15：如图12，测得丁树落在地面上的影长为2.4米，落在坡面上的影长为3米. 身高是1.6米的小王站在坡面上，影子也都落在坡面上，小林测得他的影长为1.2米，丁树多高？

影长由在水平面内转化到斜面内，让知识形成迁移，从而获取新知识和新技能.

学生的能力决定了开发实验素材的深度和广度. 从课堂走向课外，最终又回到数学事实本身. 实验教学能促进学生自主发展，实现人人皆学、处处可学、时时能学，进而积累一定的经验与策略，培养学生求真、求实的科学态度，以及“问、验、悟、用”的能力. 这样的课堂数学思维更浓了.

4. 回归事实，启思明理

在数学事实的基础上，以实验中存在的问题（操作层面、理性层面等）为契机，通过坦诚意见交推，化解心中的困惑，积累与发展经验，使经验与知识之间的相互转化形成有真实价值的实验成果.

环节4：释疑解惑，寻求指导.

运用简单的表格，汇总实验活动中的经验教训，反思实验的成败. 通过答辩透悟，经历去粗取精、去伪存真、由此及彼、由表及里的深化过程，从而调整认知结构，让结论趋向科学化、合理化与可信化，促进学生个体的成长与进步.

生16：若旗杆或树与地面不垂直怎么办？

生17：中午时刻，当测量者的影长为0时，以旗杆顶端在地面的投影为基点，当两者都有影长时，再进行测量.

生18：为了防止旗杆被台风刮倒，常见旗杆顶上被一线拉住. 此时是否有更好的方法测量旗杆的高度？

师：需要知道线与地面的接触点与旗杆的距离及线与地面所成的角，利用后续要学的三角函数知识可以计算出旗杆的高度. 有兴趣的同学可以先行研究.

生19：树梢影长太小，经常随风飘动，难于固定怎么办？

生20：在阳光充足的情况下，或无风状态下，或多次定树梢投影点，找出最密点.

生21：地面不平怎么办？

师：以被测物体的适当高度为基准，利用标杆等测量工具，找到一条平行于地平线的准线.

生22：斜坡坡面不平怎么办？

生23：取一块平整的木板置于上面.

生24：粗树杆的影长如何测量？有没有比较简洁的测量方法？

生25：类比测量跳远的距离.

实验为学生营造了想象的空间. 从抽象到具体，从粗略到精确，让学生敢说、敢想、敢做. 在回归数学事实的过程中，自我调整认知结构形成数学思维;在对实验结果进行客观描述、归纳活动经验时，学会用理性的眼光看待事物，善于提炼數学思想方法，实现明一理、通一类的飞跃.

五、实验价值

数学实验在于“做”数学、“学”数学、“用”数学.

“做”数学. 以测量问题为驱动，通过手脑并用，获取感性认识，使问题直观化、形象化、简单化、生活化、数学化. 在“做”和“思考”中积淀知识，提出新观点、生成新知识，积累基本活动经验，感受知识的鲜活，初步体验创造的激情，培养学生的批判与创新精神，为课堂教学注入新的活力.

“学”数学. 亲历知识的再现过程，经历反思和质疑，检验猜想，验证结论，让学生变被动的“听”为主动的“学”. 自主发现、解决问题，锤炼数学语言，形成层进式、沉浸式的学习习惯，以及发现式的数学意识.

“用”数学. 整合应用所学的知识，在运用中促进对知识的深入理解、思考，掌握数学基本技能，逐渐学会用数学眼光看世界，提升解决实际问题的综合能力，进而实现求真求实、科学严谨的治学态度，完善思维品质.

数学实验的本质是以数学问题为出发点，以获得数学结论为目标，以发展学生的数学学科核心素养为使命的实践活动. 教学时，建构抽象、简化、开放的数学实验环境，让教与学相互交融，使学生在良性竞争、共享互惠、协同进化中充分展示思维，激发学生对实验探究和应用的学习热情，发挥学生的情感效能，培养学生实事求是、勇于探索的创新精神，从而培养学生的数学学科核心素养，造就富有生气且充满灵性的个体.

参考文献：

[1]曹爱萍. 初中数学实验教学的研究与思考[D]. 贵阳：贵州师范大学，2017.

[2]杨超. 初中数学实验的实证研究[D]. 杭州：杭州师范大学，2016.

[3]王金水，林晴岚. 追本溯“圆” “圆”来如此[J].中国数学教育（初中版），2019（7 / 8）：94-97，102.

[4]王金水. 把握课堂追问时机  提升初中生数学思维品质[J]. 福建基础教育研究，2021（2）：57-60.