黄河流域骨干枢纽泥沙调控利用潜力评价研究

李新杰 李弘瑞 张红涛 孔德志 王远见

摘 要：为掌握黄河流域骨干枢纽的泥沙调控利用潜力，从水利枢纽的调沙潜力、输沙潜力和泥沙资源利用潜力的各特征指标出发，结合水利枢纽的共性指标，建立骨干枢纽群的泥沙调控利用潜力评价指标体系，提出基于多目标灰靶理论-累积前景理论的水利枢纽泥沙调控利用潜力量化方法。该方法利用多目标灰靶理论确定泥沙调控利用潜力评价指标体系决策矩阵，结合累积前景理论确定骨干枢纽综合前景值。采用模糊判别法对黄河流域骨干枢纽的泥沙调控利用潜力进行综合评价。由研究结果可知，小浪底水库的泥沙调控利用潜力最大，其次是刘家峡水库和三门峡水库，万家寨水库最小。

关键词：泥沙调控;灰靶理论;前景理论;模糊理论;骨干枢纽;黄河流域

中图分类号：TV697;TV882.1

文献标志码：A

doi：10.3969/j.issn.1000-1379.2021.11.008

引用格式：李新杰，李弘瑞，张红涛，等.黄河流域骨干枢纽泥沙调控利用潜力评价研究[J].人民黄河，2021，43（11）：40-45，51.

Sediment Regulation and Utilization Potentiality Evaluation of Key Reservoir in the Yellow River Basin

LI Xinjie  LI Hongrui2， ZHANG Hongtao2， KONG Dezhi  WANG Yuanjian1

（1.Yellow River Institute of Hydraulic Research， Zhengzhou 45000  China;

2.School of Electric Power， North China University of Water Resources and Electric Power， Zhengzhou 450011， China;

3.Hydrological Bureau of Yellow River Conservancy Commission， Zhengzhou 450004， China）

Abstract： In order to grasp the regulation and utilization potential ofkey reservoirs in the Yellow River Basin， the value evaluation system of sediment dynamic regulation potential of key water conservancy projects was established based on the characteristic indexes of sediment control potential， sediment transport potential and sediment resource utilization potential combined with the common indexes of water conservancy projects. Sediment dynamic control capacity quantitative method was presented based on multi-objective grey target theory and the cumulative prospect theory. The method was used to deal with index matrix by the multi-objective grey target theory and realized the quantification of the potential value by combining with the cumulative prospect theory. Finally， taking the key reservoirs of the Yellow River as an example， the fuzzy assessment method was applied to make comprehensive evaluation of sediment dynamic control potential. The results show that the Xiaolangdi Reservoir has the highest sediment dynamic regulation capacity， Liujiaxia Reservoir， Sanmenxia Reservoir and Wanjiazhai Reservoir rank the second to the fourth respectively.

Key words： sediment regulation; grey target theory; prospect theory; fuzzy theory; key reservoir; Yellow River Basin

黃河难治，根在泥沙，黄河的泥沙淤积和处置问题是长期困扰黄河治理的关键技术难题[1]，而大型水利枢纽是调节河流泥沙时空分布的重要工具[2]。目前，已经建成的黄河水沙调控工程体系在防洪减淤和水沙调控方面发挥了巨大作用[3]。然而，随着黄河流域水沙条件的变化和骨干枢纽群的长期运行，水库泥沙淤积制约着水库综合效益的发挥，流域骨干枢纽群泥沙调控利用潜力逐渐降低，影响了流域水沙调控的效果[4]。充分认识和挖掘骨干枢纽泥沙调控利用潜力，是黄河流域生态保护和高质量发展的关键问题之一[5]。

对于黄河流域骨干枢纽群而言，泥沙调控利用潜力可以理解为在一定水沙条件和当前流域水沙调控工程体系下，基于水力学及河流动力学理论，通过水库调度、人工清淤等技术，实现泥沙空间优化配置、水沙关系协调和泥沙资源利用等效益发挥的潜在利用能力。它既包括当前水沙及流域边界条件下能够认识到或者通过一定的工程技术措施能够实现的部分，又包括局限于当前工程和水沙条件而无法实现甚至无法认识到的部分，包括一切客观存在的利用潜力。

目前关于黄河流域水沙变化的研究较多，而关于黄河流域骨干枢纽群泥沙调控利用潜力的研究较少[6-7]。笔者通过分析当前黄河流域骨干枢纽群的泥沙淤积现状和调度实践，建立水利枢纽的泥沙调控利用潜力指标体系，引入灰靶理论和累积前景理论对泥沙调控利用潜力进行量化，采用模糊评判法对水利枢纽的泥沙调控利用潜力价值进行评价，从调沙潜力、输沙潜力和泥沙资源利用潜力3个方面研究骨干枢纽群的泥沙调控利用潜力，以期为黄河水沙调控提供技术支撑。

1 泥沙调控利用潜力内涵及评价指标体系

泥沙调控利用潜力是一个相对的概念：基于当前水库淤积现状和水沙条件，通过水库调度实现对泥沙的调控和输送，塑造有利于高效输沙的水沙关系，实现水库淤积形态改善和河道输沙入海能力提高的潜力。泥沙调控利用潜力需要借助泥沙资源利用，实现枢纽群泥沙调控利用能力的可持续性，从而释放水库泥沙调控的利用潜力。

根据黄河流域水沙调控的宏观背景和主要目标，从调沙潜力、输沙潜力和泥沙资源利用潜力3个方面来表征黄河流域骨干枢纽的泥沙调控利用潜力。

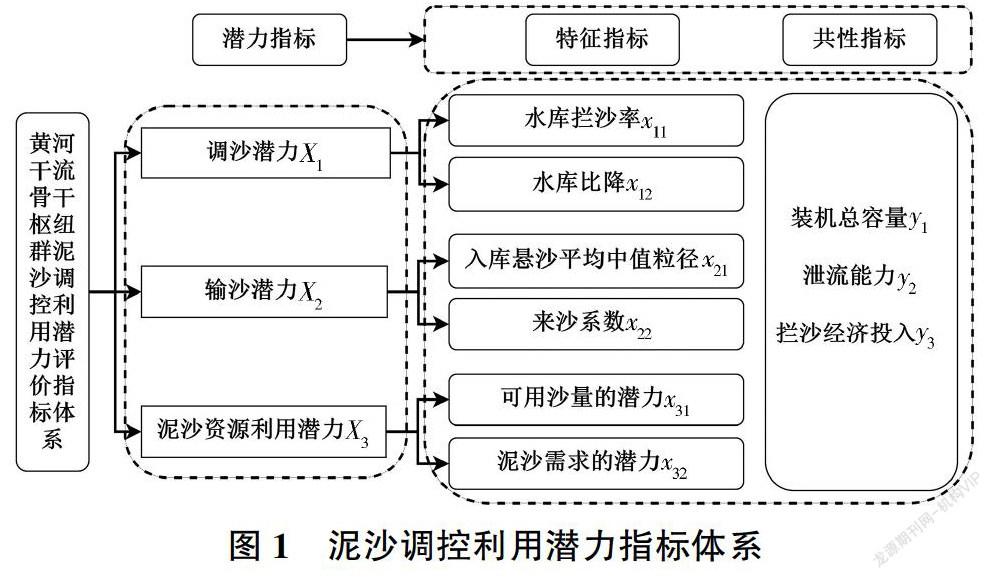
具体而言，黄河流域骨干枢纽群泥沙调控利用潜力评价指标体系由3个一级利用潜力指标（Xk）（k= 3）构成，每个一级利用潜力指标由2个特征指标（xk1，xk2）和3个共性指标（y1，y2，y3）组成。泥沙调控利用潜力指标体系见图1，其中：调沙潜力（X1）、输沙潜力（X2）与泥沙资源利用潜力（X3）为3个一级利用潜力指标，特征指标和共性指标为二级利用潜力指标。特征指标是每个一级利用潜力指标所特有的;共性指标是每个一级利用潜力指标所共有的，是各水利枢纽的固有属性。在各利用潜力指标的特征指标和共性指标基础上，计算一级利用潜力指标的利用潜力值，进而对水利枢纽的泥沙调控利用潜力进行综合评价。

1.1 调沙潜力

调沙潜力（X1）的特征指标由水库拦沙率（x11）和水库比降（x12）来表征。水库拦沙率是指水利枢纽可利用的拦沙库容占水库总拦沙库容的百分比，其公式为

x11=Vs/V0×100% （1）

式中：Vs为水库可利用的拦沙库容;V0为水库总拦沙库容。

水库比降影响水库调沙能力，比降越大，流速越快，河道调沙能力则越大。

1.2 输沙潜力

输沙潜力（X2）的特征指标由入库悬沙平均中值粒径（x21）和来沙系数（x22）组成。水库所在河道输沙潜力受多年入库悬沙平均中值粒径影响，粒径越大，泥沙沉降速度越快，水流挟沙能力越小，输沙效率越低。来沙系数是水库多年平均入库含沙量与流量的比值，作为影响水库输沙能力的判别指标，来沙系数越大，水库输沙潜力越大。

1.3 泥沙资源利用潜力

泥沙资源利用潜力（X3）的特征指标由水库所在河道可用沙量的潜力（x31）和泥沙需求的潜力（x32）组成。可用沙量的潜力用水库所在河段的多年平均输沙量表征，年输沙量的大小即表明可利用沙量的潜力大小。泥沙需求的潜力指水库所在河段防洪工程建设、堤防维修等所需要泥沙的潜力。

1.4 共性指标

共性指标由水库的装机总容量（y1）、水库泄流能力（y2）和水库拦沙经济投入（y3）3个指标构成。对于水库装机总容量指标而言，水库装机容量越大，发电效益越大，水库调控利用潜力就越大。对于水库泄流能力，泄流能力越大，水库泥沙调控利用潜力越大。水库拦沙经济投入指标是根据工程投入，结合不同水库抽沙出库的成本，估算水库拦沙经济投入，单位为元/t，其数值大小与其利用潜力大小成反比[4]。

2 泥沙调控利用潜力量化方法

2.1 多目标灰靶理论

灰色系统理论是邓聚龙在1982年提出的，以部分信息已知、部分信息未知的小样本、贫信息的不确定系统为研究对象的一门系统科学，用来解决少数据、不确定性的问题[8]。对于黄河骨干枢纽群的泥沙调控利用潜力价值体系而言，一部分信息是已知的，另一个部分信息是未知的，系统内各因素间有不确定性关系，且建立的指标体系为小样本数据[9-10]。本文选用多目标灰靶理论处理由泥沙利用潜力评价指标体系所构建的决策矩阵，其主要指标包括正（负）靶心和靶心系数。正（负）靶心：根据指标性质（成本型和收益型）确定指标的正（负）靶心并生成正（负）标准序列。靶心系数：水库各指标利用潜力数据与正（负）靶心标准序列进行比较得出正（负）靶心系数，进而从两个方向实现利用潜力指标的量化。

设多指标评价体系有n个水利枢纽对应n个利用潜力。方案集S={s1，s2，…，sn}，各水利枢纽对应的各一级利用潜力指标的m个指标（特征指标和共性指标）组成指标集O={o1，o2，…，om}。方案si对指标oj的效果样本值为xij（i= …，n;j= …，m），则方案集S对指标集O的决策矩阵（效果样本矩阵）X为

X=x11…x1m

xn1…xnm（2）

令

Zj=1n∑ni=1xij（3）

对决策矩陣X中元素进行处理，记为yij，首先将各利用潜力指标的性质进行区分，若对应指标为效益型，则有：

yij=xij-ZjZj（4）

若对应指标为成本型，则有：

yij=Zj-xijZj（5）

变换后的矩阵记为

D=（yij）n×m（6）

将矩阵D规范化，得到规范决策矩阵R：

R=（rij）n×m（7）

其规范化方法为

rij=yijmaxj（yij）（8）

以上变换将决策矩阵的元素值限制在[-1，1]区间。

确定决策矩阵中每个指标的正（负）靶心，其中：

r+j=max（rij）（9）

r+=（r+1，r+2，…，r+m）（10）

r+为灰靶决策最优效果向量，称为各利用潜力指标的正靶心。

r-j=min（rij）（11）

r-=（r-1，r-2，…，r-m）（12）

r-为灰靶决策最劣效果向量，称为各利用潜力指标的负靶心。

根据多目标灰靶理论，每个指标与靶心的接近程度反映了指标的优劣。本文采用灰色关联分析方法计算每个指标与正（负）靶心的正负关联系数。

设r+j与r-j分别为正、负靶心，则正、负靶心系数分别为

ξ+ij=miniminjrij-r+j+ρmaximaxjrij-r+jrij-r+j+ρmaximaxjrij-r+j（13）

ξ-ij=miniminjrij-r-j+ρmaximaxjrij-r-jrij-r-j+ρmaximaxjrij-r-j（14）

式中：ρ∈[0，1]，为分辨系数，一般取ρ=0.5[11]。

由正靶心系数所表示的利用潜力指标值与一级利用潜力指标的大小成正比，由负靶心系数所表示的利用潜力指标值与一级利用潜力指标的大小成反比，且各利用潜力指标的正（负）靶心系数限制在（0，1]之间。获取正（负）靶心系数即对二级利用潜力指标实现了量化。

2.2 累积前景理论

累积前景理论由前景理论改进而来[12]。相较于前景理论，累积前景理论实现了多结果的综合分析，允许收益和损失有不同的权重函数。前景价值的大小由价值函数和决策权重共同决定[13]。累积前景理论通过设置一个参考点，根据参考点确定数据指标的收益或损失情形进而选择不同的价值函数和权重函数。价值函数对于本评价体系而言，其含义是利用潜力指标价值体系在面对收益情形时是风险厌恶的，在面对损失情形时是风险追寻的。权重函数对于本评价体系而言，用于平衡各利用潜力指标在评价体系中的结构占比，寻求前景价值最大化。

前景价值的表达式为

V=∑ni=1π（pi）v（xi）（15）

式中：V为前景值;π（p）为决策权重;v（x）为价值函数。

各指标对应的前景价值函数的表达式为

v（rij）=（1-ξ-ij）α

-θ-（ξ+ij-1）β（16）

式中：参数α和β分别为收益和损失区域价值幂函数的凹凸程度，一般取α=β=0.88;系数θ为损失和收益的相关系数，一般取θ=2.25[14]。

负靶心系数为参考值则各利用潜力指标优于负靶心，由前景理论可知面对收益情形时是风险厌恶的，故把v+（rij）=（1-ξ-ij）α作为正前景价值函数;正靶心系数为参考点则各利用潜力指标劣于正靶心，由前景理论可知面对损失情形时是风险追寻的，故把v-（rij）=-θ[-（ξ+ij-1）]β作为负前景价值函数[15]。

设利用潜力指标价值体系面临收益和损失时的前景权重函数分别为π+（wj）和π-（wj），其表达式[16]分别为

π+（wj）=wr+j[wr+j+（1-wj）r+]1/r+（17）

π-（wj）=wr-j[wr-j+（1-wj）r-]1/r-（18）

式中：wj為每个指标的权重;前景权重函数中的参数r+=0.61，r-=0.69[14]。

则方案S的指标集O的综合前景值为

Vi=∑mj=1v+（rij）π+（wj）+∑mj=1v-（rij）π-（wj）（19）

式中：Vi为一级利用潜力指标的综合前景值（利用潜力值）。

计算出各水利枢纽的一级利用潜力指标的综合前景值，量化一级利用潜力指标，构建综合前景值矩阵。

2.3 最优指标权重的确定

设各水利枢纽的各一级利用潜力指标中各二级利用潜力指标权重向量为w=（w1，w2，…，wm），且∑mj=1wj=1。其中aj≤wj≤bj，0≤aj≤bj≤1。对于每个水利枢纽其各一级利用潜力指标的综合前景值总是越大越好，因此建立优化模型，其目标函数为

max V=（V1，V2，…，Vn）=∑ni=1∑mj=1v+（rij）π+（wj）+

∑ni=1∑mj=1v-（rij）π-（wj）（20）

约束条件为

aj≤wj≤bj，0≤aj≤bj≤1

∑mj=1wj=1，wj≥0

（i= …，n;j= …，m）

式中：max V为一级利用潜力指标中最大综合前景值。

通过Excel表格中的规划求解工具，求解出上述目标函数的最优解，得到最优权重w*=（w*1，w*2，…， w*m），用于综合前景值的计算。

3 基于模糊判别法的调控利用潜力价值评价

3.1 模糊判别法

本文所采用的模糊评判法是基于模糊数学理论的一种决策方法，因其良好的实用性，已被广泛应用于各个领域[17]。基于已构建的水利枢纽泥沙调控利用潜力价值体系的一级利用潜力指标量化矩阵，结合模糊综合评判法，分析各一级指标所对应的最优选项，对各水利枢纽的泥沙调控利用潜力进行量化和评价。

本文将泥沙调控利用潜力价值分为5个级别，即评判集A={A1（很高），A2（较高），A3（一般），A4（较低），A5（很低）}。本文采用高斯型隶属函数确定各一级利用潜力指标综合前景值对不同评语的模糊子集，其形式如下：

f（x，δ，c）=e-（x-c）2/（2δ2）（21）

式中：δ和c为高斯隶属函数的两个参数，c用于确定高斯函数的曲线中心，c1=1，c2=0.75，c3=0.5，c4=0.25，c5=0，代入式（21）可得到5个评判等级对应的隶属函数;δ为高斯函数的宽度参数，为了保证评判结果的区分度，可对δ进行调整，选取合适的值。

将各一级利用潜力指标的综合前景值Vik（k= …，K，K为一级利用潜力总数）代入式（21），得到方案集i隶属于评判集A的模糊评判矩阵Fi：

Fi=fA1（Vi1）…fA5（Vi1）

fA1（Vik…fA5（Vik）（22）

式中：fAk（Vik）为Vik在不同评判等级At（t= …，5）的隶属度。

由各级利用潜力指标之间的关联性，取其权重向量λ=（λ1，λ2…，λK），并且∑Kk=1λk=1。对模糊评判矩阵Fi和权重向量λ采用算子M作模糊乘积运算，线性加权后得到模糊评判结果Si：

Si=λFi=（si（A1），si（A2），si（A3），si（A4），si（A5））（23）

式中：si（At）（t= …，5）为水库i相对于评判等级At的隶属度，表示水库i由At可描述的程度。

通过式（23）可确定各水利枢纽泥沙调控利用潜力在各评判等级下的隶属度，根据最大隶属度原则，筛选出利用潜力指标最优的水利枢纽。

将评判集A量化为

A=A1A2A3A4A5=9585756555（24）

水利枢纽i的泥沙调控利用潜力价值评价得分为

Zi=∑5t=1si（At）At（25）

式中：Zi为各水利枢纽的泥沙调控利用潜力的最终评分。

黄河流域各水利枢纽泥沙调控利用潜力的量化，在一定程度上反映了各水利枢纽泥沙调控利用潜力的大小。

3.2 评价流程

泥沙调控利用潜力评价流程：首先，根据样本矩阵计算各二级利用潜力指标并构建决策矩阵，利用灰靶理论对决策矩阵进行处理，确定各利用潜力指标的正（负）靶心，确定正（负）靶心系数矩阵;其次，结合累积前景理论以前景值最大化为目标，量化利用潜力，得到各水库的调沙潜力、输沙潜力和泥沙资源利用潜力值;最后，通过模糊评判法对每个水库的泥沙调控利用潜力进行综合评价，量化各水库的泥沙调控利用潜力。评价流程见图2。

4 实例研究

4.1 数据选取

选取黄河流域骨干枢纽龙羊峡水库、刘家峡水库、万家寨水库、三门峡水库和小浪底水库为研究对象。各个水库的库容特征值见表1。由于龙羊峡水库是黄河上游的龙头水库，库容247亿m 年均输沙量仅为0.263亿t，库容大，入库沙量小，入库沙量与库容相比很小，因此不参与泥沙利用潜力评价。各水库相关原始及观测数据来自中国泥沙公报及相关文献[18-21]。

4.2 算例分析

各水利枢纽的二级利用潜力指标初始值见表2。其中刘家峡水库、万家寨水库和三门峡水库拦沙库容已经淤满，水库已经没有拦沙能力，因此水库拦沙率为0。

（1）利用潜力指标数据的预处理。以水库的一级利用潜力指标调沙潜力为例，调沙潜力下的水库拦沙率、水库比降、水库装机总容量和水库泄流能力指标为效益型指标，水库拦沙经济投入为成本型指标。依据多目标灰靶理论，对调沙潜力指标的决策矩阵进行规范化得到规范决策矩阵，确定各二级指标的正（负）靶心，并计算出调沙潜力的正（负）靶心系数矩阵，结果见表3。

同理可依次计算出输沙潜力、泥沙资源利用潜力的正（负）靶心系数矩阵。

（2）计算各利用潜力指标的综合前景值。為使特征指标和共性指标在各一级利用潜力指标量化评价中占比适中，对各指标权重wt进行限制。设特征指标：0.1≤wt≤0.3（t=1，2）;共性指标：0.1≤wt≤0.3（t= 4，5）。以各水库的一级利用潜力指标前景值最大为目标获取调沙潜力、输沙潜力和泥沙资源利用潜力下各特征指标、共性指标的最优指标权重，见表4。

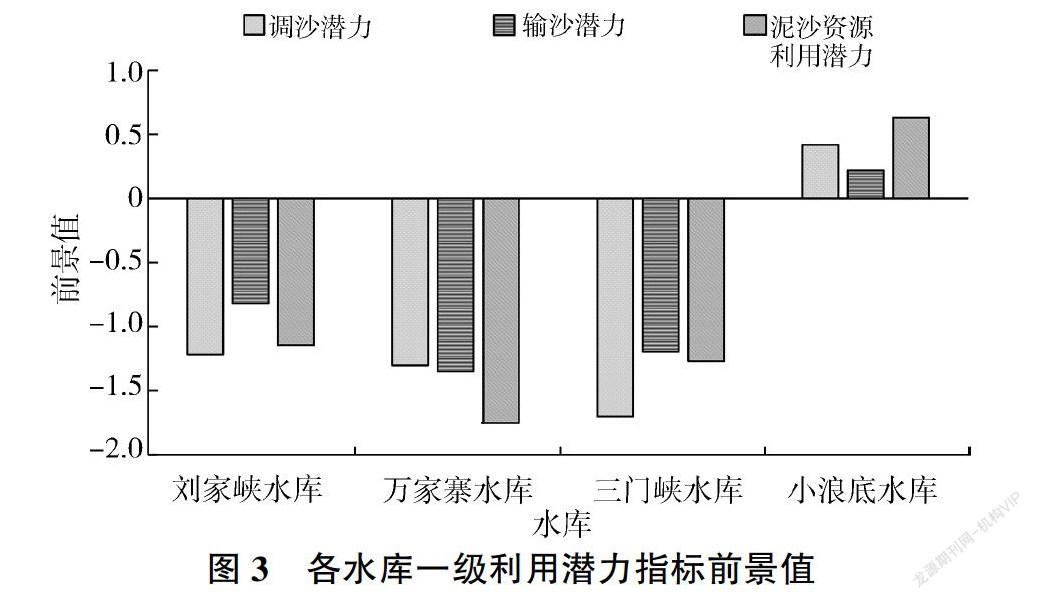
获取各利用潜力指标的最优权重，计算出调沙潜力、输沙潜力和泥沙资源利用潜力的综合前景值，如图3所示。

由图3可知，小浪底水库调沙潜力前景值（0.42）、输沙潜力前景值（0.22）和泥沙资源利用潜力前景值（0.63）均为最大，三门峡水库的调沙潜力前景值最小（-1.70），万家寨水库的输沙潜力前景值（-1.34）和泥沙资源利用潜力前景值（-1.75）最小。基于各水库调沙潜力、输沙潜力和泥沙资源利用潜力的前景值，利用模糊判别法对水库的泥沙调控利用潜力进行综合评价。

为保证价值评分的区分度，经多次调整，选取δ=0.8，建立模糊隶属度矩阵，计算各利用潜力的模糊判别矩阵，得出各水利枢纽泥沙调控利用潜力对5个评判等级的隶属度，见表5。

由表5可知，根据最大隶属度原则，4个水库的泥沙动态调控利用潜力的最大隶属度在等级A5所占比重较大，其中小浪底水库在等级A1、A2、A3的隶属度比重均较大，说明小浪底水库的泥沙调控利用潜力优于其他3个水库。而万家寨水库在等级A5隶属度比重最大，说明万家寨水库的泥沙调控利用潜力最低。

计算各水库的泥沙调控利用潜力价值评分，结果表明：

小浪底水库的泥沙调控利用潜力价值评分最高（74.5），刘家峡水库次之（65.3），三门峡水库第三（63.9），万家寨水库最小（63.5）。各水利枢纽的评分的高低一定程度上代表其泥沙调控利用潜力的大小。结合水库所在位置及其淤积现状可知其利用潜力评价结果符合实际情况，表明此评价方法合理且有效。

5 结 论

针对水库泥沙调控影响因素，构建包含调沙潜力、输沙潜力和泥沙资源利用潜力3个一级利用潜力指标、6个特征指标和3个共性指标的黄河流域骨干枢纽群泥沙调控利用潜力指标体系，提出基于灰靶理论和累积前景理论的泥沙调控利用潜力量化方法。充分考虑在评价量化时对待成本型和效益型指标的态度，构建最优前景价值模型，得到各一级利用潜力指标的最优权重，并计算其综合前景值。最后，采用模糊判别法对各水利枢纽的泥沙调控利用潜力价值进行综合评价，实现了水利枢纽泥沙调控利用潜力的量化，直观地表明现有水利枢纽在泥沙调控中所占比重及客观存在的利用潜力。

本文算例表明，目前在黄河流域骨干枢纽群（刘家峡、万家寨、三门峡和小浪底）中，小浪底水库泥沙调控利用潜力最大，刘家峡水库位于第二位，三门峡水库和万家寨水库的泥沙调控利用潜力位于第三、四位且评分相近，表明这两个水库泥沙调控利用潜力相近。本文提出的基于多目标灰靶理论和累积前景理论的泥沙调控利用潜力量化方法能够有效地分析和评价黄河流域现有骨干枢纽的泥沙调控利用潜力，为今后黄河流域泥沙动态调控和资源利用提供依据。

参考文献：

[1] 胡春宏，陈绪坚，陈建国.黄河水沙空间分布及其变化过程研究[J].水利学报，2008，39（5）：518-527.

[2] 张金良，练继建，张远生，等.黄河水沙关系协调度与骨干水库的调节作用[J].水利学报，2020，51（8）：897-905.

[3] 江恩慧，王远见，田世民，等.流域系统科学初探[J].水利学报，2020，51（9）：1026-1037.

[4] 王远见，江恩慧，张翎，等.黄河流域全河水沙调控的可行性与模式探索[J].人民黄河，2020，42（9）：46-51.

[5] 胡春宏.黃河干流泥沙空间优化配置研究（Ⅱ）：潜力与能力[J].水利学报，2010，41（4）：379-389.

[6] 申冠卿，张原锋，张敏.黄河下游高效输沙洪水调控指标研究[J].人民黄河，2019，41（9）：50-54.

[7] 李新杰，郜国明，朱亮，等.黄河潼关站水沙关系频率及协调度分析研究[J].人民黄河，2020，42（5）：47-51.

[8] 邓聚龙.灰预测与灰决策[M].武汉：华中科技大学出版社，2002：222.

[9] 刘思峰，杨英杰，吴利丰.灰色系统理论及其应用[M].7版.北京：科学出版社，2014：63-64.

[10] 曲武.灰色系统理论在水文地质实践中的应用探讨[J].长江技术经济，2020，4（增刊1）：90-91，104.

[11] SUN C Y， YANG X J， ZHAI J J. Doctoral Innovation Ability and Innovation Performance Evaluation Model[C]//Springer Nature. International Conference on Communications， Information Management and Network Security. Paris： Atlantis Press， 2016：155-157.

[12] TVERSKY A， KAHNEMAN D. Advances in Prospect Theory： Cumulative Representation of Uncertainty[J]. Journal of Risk and Uncertainty，1992，5（4）：297-323.

[13] 谭晓娟.前景理论评述[J].中国集体经济，2012（1）：87-88.

[14] 隋大鹏，张应语，张玉忠.前景理论及其价值函数与权重函数研究述评[J].商业时代，2011（31）：73-75.

[15] 刘勇，FORREST Jeffrey，刘思峰，等.基于前景理论的多目标灰靶决策方法[J].控制与决策，201 28（3）：345-350.

[16] 徐青山，丁一帆，颜庆国，等.大用户负荷调控潜力及价值评估研究[J].中国电机工程学报，2017，37（23）：6791-6800，7070.

[17] YAN R， HU Z H， WU C W， et al. Evaluation and Prediction of Water Quality in the Yangtze River Based on Fuzzy Comprehensive Evaluation Method[J].Journal of Plant and Environmental Research，2020，4：1-18.

[18] 江恩慧，王远见，李军华，等.黄河水库群泥沙动态调控关键技术研究与展望[J].人民黄河，2019，41（5）：28-33.

[19] 王国玉，于连青.黄河源区唐乃亥站水沙特性初步分析[J].青海环境，2005，15（2）：63-65，71.

[20] 陈翠霞，安催花，罗秋实，等.黄河水沙调控现状与效果[J].泥沙研究，2019，44（2）：69-74.

[21] 高宗军，冯国平.黄河水沙变化趋势及成因分析[J].地下水，2020，42（1）：147-151.

【责任编辑 张 帅】