基于实例结构的不完备多标签学习
2021-12-08陈天柱李凤华郭云川李子孚
陈天柱,李凤华,郭云川,李子孚
(1.中国科学院信息工程研究所,北京 100093;2.中国科学院大学网络空间安全学院,北京 100049;3.中国电子科技集团公司信息科学研究院,北京 100086)
1 引言
物联网中实体、资源和服务常用唯一标识来识别,每个标识可能包含多个具有语义信息的标签。由于物联网中资源的海量性,采用人工方式标注资源的语义面临巨大挑战。为了自动标注语义,学术界和工业界提出了多标签学习技术。然而,在一些应用场景中,训练集数据由网络志愿者标记而获得,其通常呈现标签缺失的现象[1]。
现有标签缺失下的多标签学习方法主要利用标签关联来填充缺失标签。这些方法大体可分为显式标签关联法和隐式标签关联法。其中,显式标签关联法的核心思想是利用标签向量直接计算标签关联,并约束预测标签也具有该关联。例如,Wu等[2]利用标签向量计算了标签相似度,并约束语义相似标签的预测向量也相似。Li 等[3]从维基百科等辅助源中抽取标签知识创建标签关联矩阵。Wu等[4]通过实例特征向量和标签向量直接构建无向标签关联图,在此基础上融合标签语义层次结构(例如,动物标签是马标签的父节点)创建了标签关联混合图。然而,上述方法仅利用标签间的直接关联,忽略了非直接关联,这使这些方法的预测表现通常较差。
隐式标签关联法基于低秩假设,利用随机投影、典型相关分析、线性变化等方法压缩高维标签为低维空间。随后在低维空间中预测标签并将预测标签翻转到原标签空间而获得预测标签。其中,隐式标签关联嵌入标签压缩中。例如,Zhang 等[5]利用典型相关分析技术挖掘压缩标签与预测标签间的线性关联,从而将标签关联蕴含于多标签学习中。Yu 等[6]在特征矩阵低秩假设下,基于矩阵低秩分解技术俘获了拟合矩阵低秩结构。然而,上述方法并未有效解决标签缺失下相似度准确度量问题,也未结合显式关联与隐式关联来解决标签缺失下的多标签标记问题。此外,在标签完备情况下,标签排序[7-8]也是提升模型预测精度的重要方法。然而,现有工作很少从标签排序的角度来解决标签缺失下的多标签标记问题。
针对上述不足,本文从实例的特征和标签结构出发,利用标签矩阵低秩结构和数据标签流型结构来补全缺失标签,利用加权排序损失体现标签对数据的相关程度并降低正关系学为负关系所带来的模型偏差程度。具体地,通过确保数据预测标签几何相似度与数据标签几何相似度的一致性来俘获数据流型结构;通过度量完备标签下和不完备标签下的排序损失来区分正负标签对实例的相关程度。实验结果表明本文方案优于典型的标签缺失下的多标签学习方案。本文的贡献如下。
1) 本文设计了新的流型结构,该结构降低了对标签缺失率的依赖。具体地,本文假设实例正标签是准确标记的,利用k-means 聚类方法对每个标签所有正实例的特征向量进行聚类,并利用类中心的最小主角计算标签相似度。同时,本文通过度量完备标签下和非完备标签下的排序损失,提出了新的排序正则化方法。
2) 为高效优化目标函数,本文松弛目标函数精确解为非精确解,提出了线性ADMM(LADMM,linear alternating direction method of multipliers)。通过线性近似迭代获得子问题的近似解,该近似解可确保线性ADMM 的收敛性。
3) 在6 个数据集上的实验结果表明,本文方案优于代表性的标签缺失下的多标签学习方案。在一些评估标准下,本文方案的精度比最好的对比方案提升了10%以上。
2 相关工作
标签关联法是处理标签缺失情况下多标签标记问题的一般方法,其可分为显式方法和隐式方法。在显式方法中,Li 等[3]提出包含特征输入层、标签输出层和潜标签输出层的三层玻尔兹曼机,并利用潜输出层学习高阶标签关联,同时利用标签先验知识来俘获标签关联,利用其正则化模型。Wu等[4]以标签为节点,以标签一致性和实例相似度构建节点无向边,以标签语义层次构建节点有向边,创建标签关联混合图。其中,标签语义层次是指某一标签的语义信息包含了另一标签的语义信息,如植物标签和玫瑰标签。Zhu 等[9]利用标签在数据集上的分布计算标签相似度,并确保相似度高的标签的标签预测分布距离小,相似度低的标签的标签预测分布距离大。具体地,将训练集聚类成子集,在子集和数据集中分别俘获局部和全局标签结构。Huang 等[10]从缺失训练数据中训练高阶标签关联,对每个标签学习与其最相关的特征而获得数据的低维表示。该方案同时学习标签关联与低维表示。然而,上述方法将缺失标签看作负标签来计算标签关联,造成标签直接关联度量错误,该错误随着标签缺失率的变大而越来越不准确。同时,这些方法也忽略了标签非直接关联。
针对以上不足,研究者提出隐式方法来提升模型预测精度,其大体分为基于标签矩阵方法和基于拟合矩阵方法。基于标签矩阵方法的核心思想是利用典型相关分析和线性变化等技术压缩高维标签空间为低维空间,随后在低维空间中预测标签并将其翻转到原标签空间。例如,Tai 等[11]对标签矩阵做奇异值分解,利用奇异值向量矩阵(低维正交矩阵)做投影矩阵,利用其转置矩阵做解码矩阵(正交矩阵的逆矩阵是其转置矩阵)。Zhang 等[5]利用2 个线性变换分别压缩标签和预测标签,通过典型相关分析寻找压缩标签空间最优预测方向来俘获标签关联。随后,在文献[5]方案的框架下,Zhang 等[12]保持标签距离结构与嵌入标签距离结构一致性,并最大化数据预测标签与其他数据预测标签的边界距离,提出了嵌入标签可区分性和可预测性的多标签学习方案。然而,随着标签规模的变大,确保整体数据距离结构的方案[12]需要极大的计算开销。针对该不足,Jin 等[13]仅约束实例预测标签与其嵌入标签距离小于实例预测标签与其近邻数据嵌入标签距离。
在基于拟合矩阵的方法中,Yu[6]等分解拟合矩阵为2 个低维矩阵,利用一个矩阵压缩特征空间为低维空间,另一个矩阵拟合压缩后的特征从而获得标签预测。此外,Jing 等[14]为俘获有效标签个数,约束拟合矩阵核范数从而实现拟合矩阵低秩结构,同时引入流型结构来确保特征相似度高的数据的预测标签相似度也高。Li 等[1]利用与标签个数等维的标签关联方阵来映射实例标签向量,从而恢复缺失标签,并利用一个具有低秩结构的去噪声编码器来学习标签关联方阵。Zhu 等[9]分解标签矩阵为2 个低维矩阵的和,利用一个矩阵表示标签的潜标签空间,另一个矩阵表示原始标签投影到潜标签空间的投影矩阵。然而,上述方法未结合标签显式关联和隐式关联来解决标签缺失下的标签标记问题。Li等[15]对标签矩阵做低秩分解来补全缺失标签,并利用希尔伯特−施密特独立性准则来俘获标签空间和特征空间的关联,从而提升模型预测精度。此外,Gupta 等[16]将训练集聚成多个子类,基于单词嵌入方法的思想,分别将每个子类的数据实例和其最近邻实例映射为主题模型中的单词和上下文,利用Skip Gram Negative Sampling 将每个实例的特征向量和标签向量嵌入低维特征空间和标签空间上。进一步地,Liu 等[17]利用平滑剪裁的绝对偏差和最小最大凹惩罚两类非凸函数来消除子类数据预测时的模型偏差。
实例正标签比其负标签更能体现实例语义信息,约束模型正标签输出值大于负标签输出值可正则化模型。基于此观察,研究者针对标签完备情况,利用线性模型、支持向量机、神经网络提出了各种标签排序方案。Usunier 等[18]基于有序加权平均函数和铰链函数提出了有序加权排序损失函数。Weston 等[7]利用铰链函数来近似0-1 排序损失,提出了函数性质为光滑的加权损失函数。然而,上述方案利用传统的数据特征作为模型输入,导致预测精度较低。Gong 等[8]训练了包含几个卷积层和dense 连接层的神经网络结构,以近似处理后的加权损失函数为基础构造top-k 排序损失,提出了基于深度卷积排序的图像多标签标记方法。Durand 等[19]以4 096 维的深度图像特征为模型输入,利用2 个潜变量分别预测标签的正向证据和负向证据。标签排序已广泛用于多媒体数据标记、语音标记中,并获得了较大成功,然而标签排序很少用于解决标签缺失下的多标签学习问题。
3 模型描述
3.1 模型动机
模型流型正则和标签排序正则步骤如图1 所示。本文研究动机基于如下3 个事实。1) 在较小规模和中规模标签的数据集中,标签矩阵和特征矩阵通常呈现一定的低秩结构。通过学习标签矩阵和特征矩阵的低秩结构来俘获标签内在关联,并利用该标签关联补充缺失标签。2) 对于2 个在特征向量上相似度越高的实例,其标签向量也越相似;对于2 个在特征向量上相似度不高的实例,其标签向量也不相似。利用实例准确的特征信息来度量实例相似度,并利用该相似度约束预测标签的相似度以实现缺失标签补全。3) 实例的正标签比负标签更能描述实例的语义信息,因此在模型训练过程中确保正标签的输出值大于负标签的输出值具有较大意义。综上所述,本文从低秩结构出发俘获了标签间的隐式关联;利用数据流型结构确保数据特征间距离与标签间距离的一致性,进而俘获了标签显式关联;利用标签加权排序区分了正负标签对数据的描述能力,俘获了每个实例的标签显式关系。
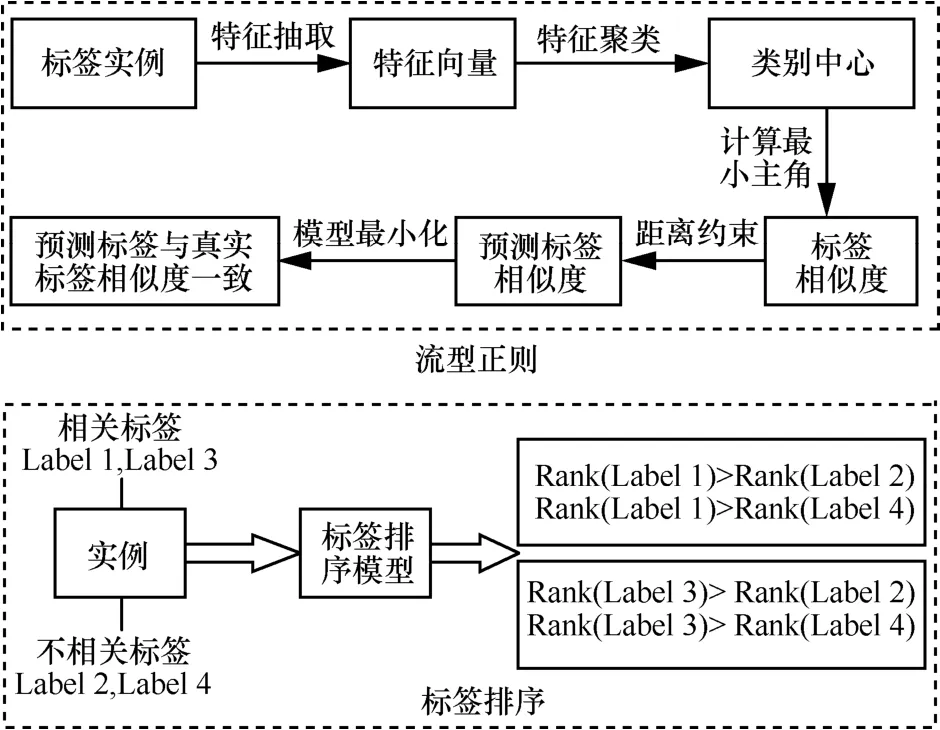
图1 模型流型正则和标签排序正则步骤
3.2 标签标记流程
本节简略介绍标签标记过程,其可粗略分为4 个子过程:训练集处理、模型建模、模型训练和标签标记,如图2 所示。训练集处理过程中,首先,专业人员根据现实需求和数据语义信息挑选标签并制定标签字典。然后,标签标记者从标签字典中挑选合适的标签来标记收集的数据,从而形成训练集。由于标记者工作疏忽,训练集中的数据可能呈现标签缺失、标签冗余和标签噪声现象。最后,专业人员对训练集数据做特征处理,将数据转化为可度量形式。例如,依据图像数据的纹理、色彩和像素信息将数据转化为特征向量表示。模型建模过程根据训练集特点,选取线性模型、随机森林模型和深度学习模型来预测数据标签,并根据标签关联关系、流型结构和L2 范数等对模型进行正则化。模型训练过程根据目标函数的特点,挑选恰当的优化方法来最小化目标函数。典型的优化方法包括梯度下降法、线性搜索法、牛顿法和翻转牛顿法等。标签标记过程将检测数据的向量表示传递给预测模型获得数据标签预测。本文标签标记过程不涉及训练集处理步骤。
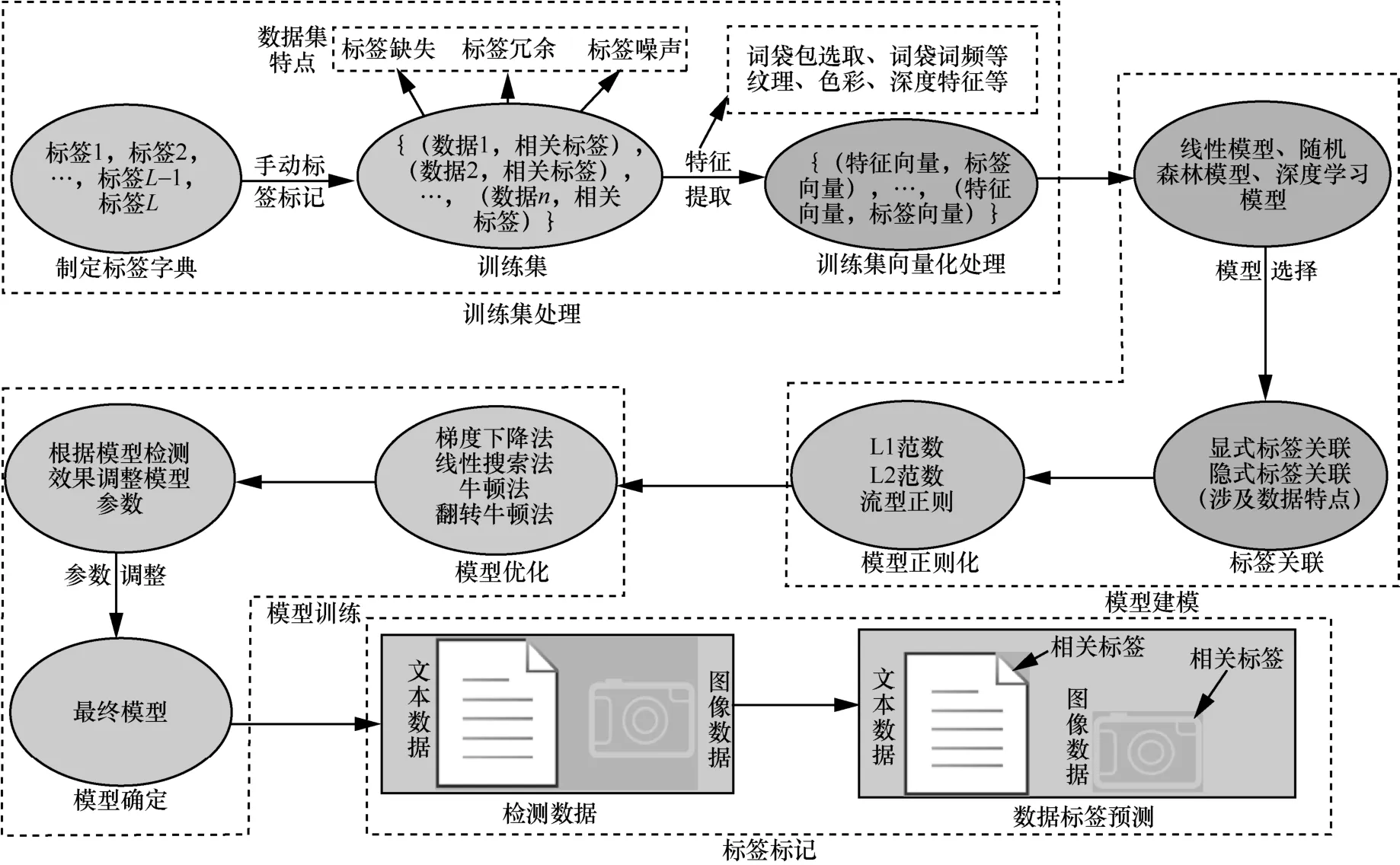
图2 标签标记流程
3.3 拟合矩阵的低秩结构


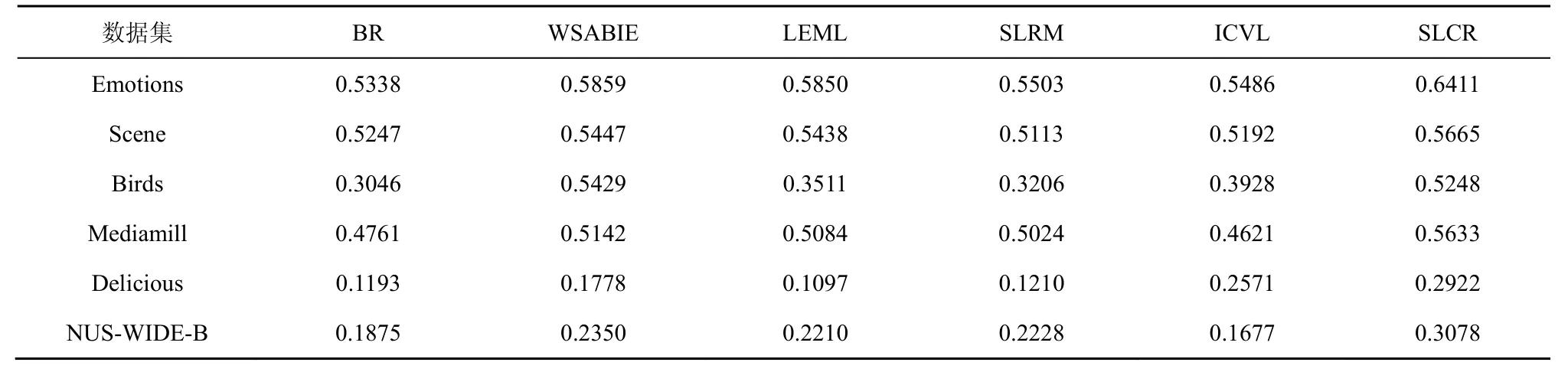
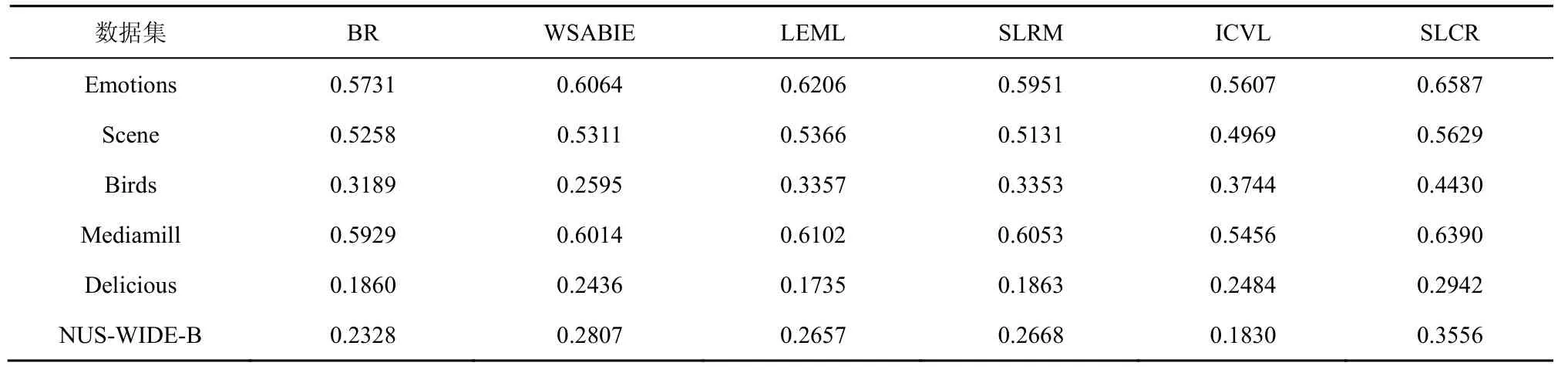
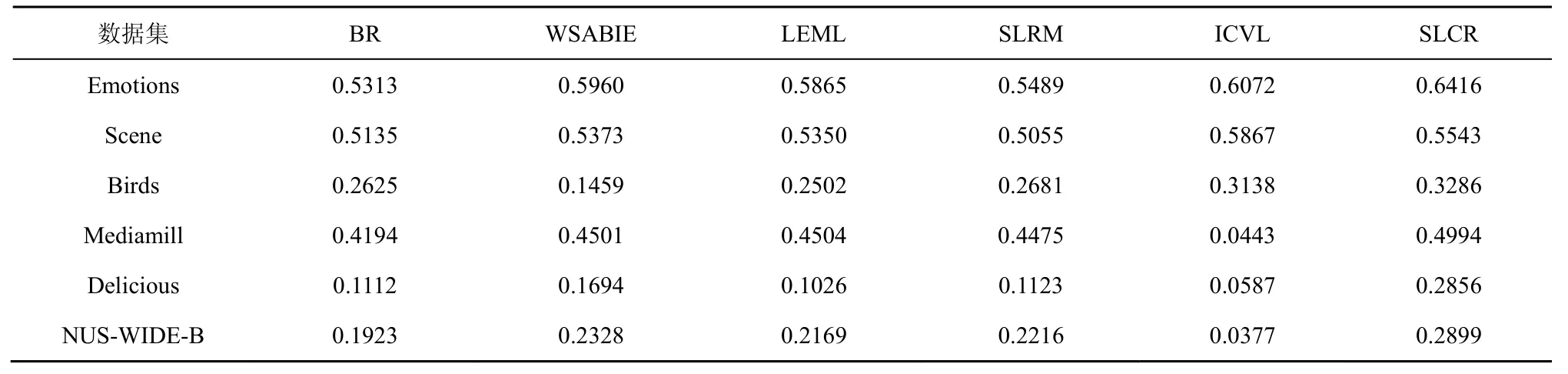
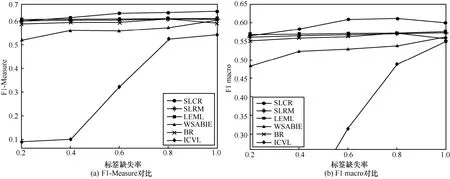
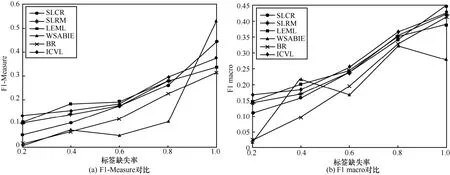
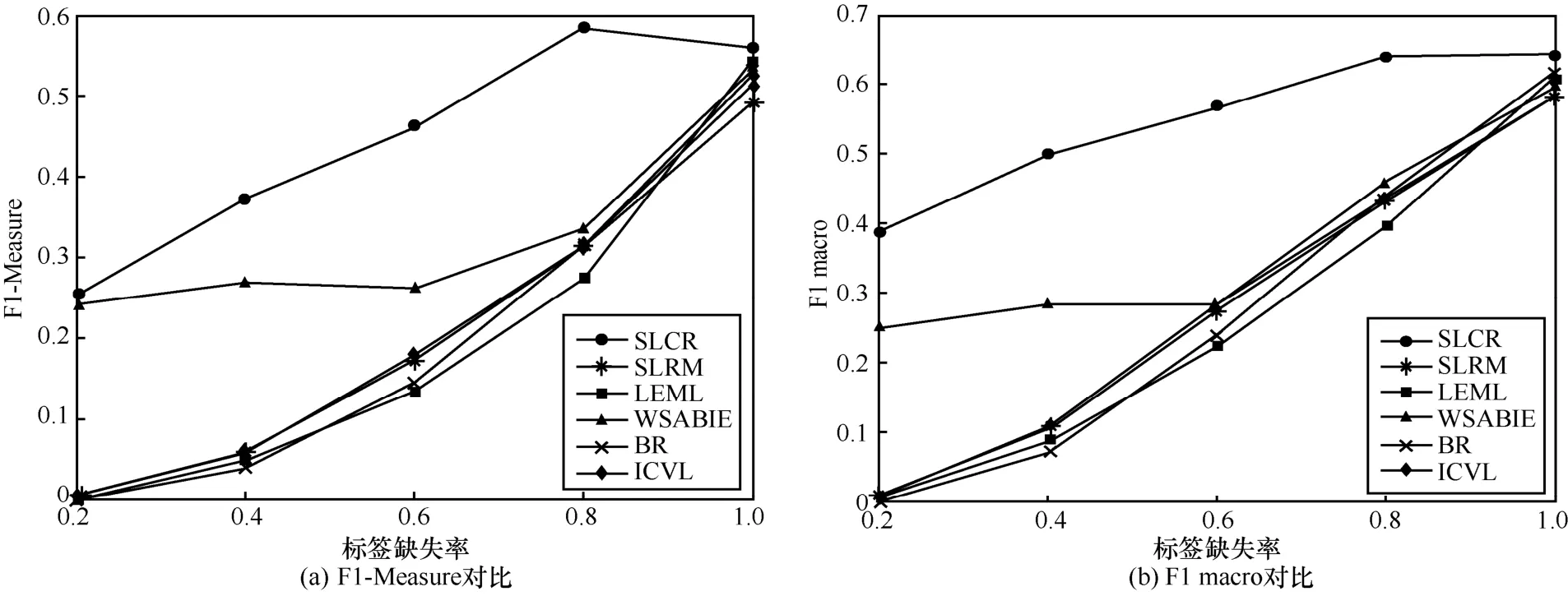
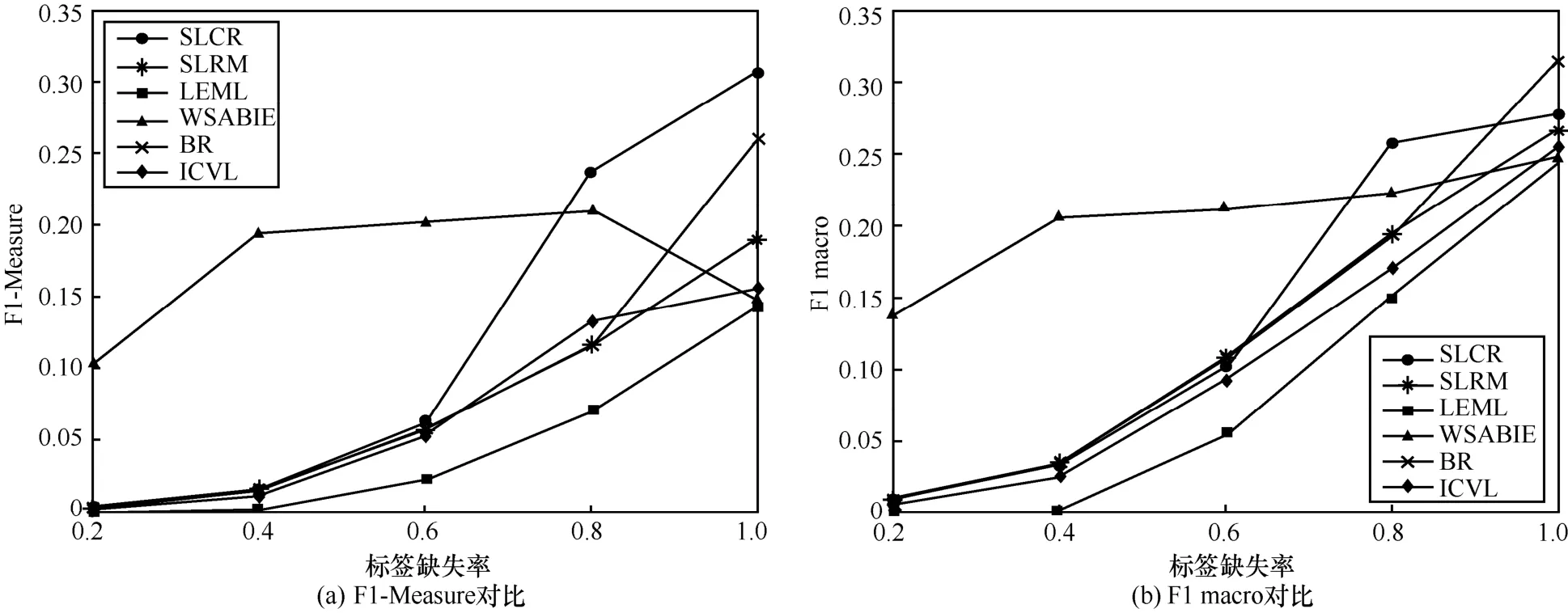
其中,k0用于约束拟合矩阵的秩,约束条件rank(M) 其中,参数k1与k0一一对应。 机器学习的核心目标是设计一个在训练集和检测集上都具有较好效果的算法。研究者们设计了一些正则化方法[21]来减少测试误差(可能以增大训练误差为代价)。正则化方法大体分为两类:控制模型复杂度、控制实例的几何结构[22]。本节利用实例分布设计了一个流型正则用于控制实例的几何结构,其核心挑战是寻找一个相似度度量函数来满足如下性质:对于任何2 个实例,如果两者的特征向量越相似,两者的预测标签距离就越小,反之亦然。 3.4.1 几何相似度 本节利用k-means 聚类方法对每个标签所有正实例的特征向量进行聚类,其中特征向量间的距离采用欧氏距离来度量。具体地,第i个标签对应正实例聚成p个类,簇中心集为Si,每个元素s∈S是一个d维特征向量。对于任何一个簇中心s和簇中心集S,本节用最小主角来度量s到S的距离dist (s,S)[23],即 其中,sT是s的转置向量。基于该距离定义,本节定义标签i与标签j的几何相似度为 3.4.2 标签预测距离 融合几何相似度与标签预测距离,本文获得如下形式的流型正则 排序正则的核心目标是确保每个实例的正标签排在其负标签的前面,可定义为 其中,(i,j)p,n={x|实例x的第i个标签是正标签,第j个标签是负标签}。为实现该目标,本文定义标签完备下任意标签对的排序损失。 3.5.1 标签完备下的排序损失 本文假设训练集D中所有实例都被完全标记,即任意实例x的任意标签i和标签j为正标签或负标签,不存在任何缺失。针对该情况,对于任意标签i和标签j的排序损失定义为 其中(i,j)n,p={x| 实例x是的第i个负标签,实例x的第j个标签是正标签},铰链损失h(j,i,x)为max {0,1+M jx−M ix}。因此,所有标签对的排序损失和为实例排序损失。由于无法区分一个实例不同正标签对实例描述程度的差异,本文未对实例正标签进行排序;同理,本文也未对实例负标签进行排序。 3.5.2 非完备标签下的排序损失 针对任意标签对(i,j),本文假设其未被完全标记,即训练集D中必存在一实例,其标签i和标签j存在一个标签缺失。针对该情况,训练集D中的所有实例可分为5 个类别:(i,j)p,m、(i,j)n,m、(i,j)m,p、(i,j)m,n和(i,j)m,m。其中,(i,j)p,m={x| 实例x的第i个标签是正标签,第j个标签是缺失标签},剩余4 种类别的定义类似该定义。上述5 种情况的排序损失函数 rli (i,j)p,m、rli (i,j)n,m、rli (i,j)m,p、rli (i,j)m,n和 rli (i,j)m,m分别定义为 其中,θi和θj分别是标签i和标签j的正实例个数与整体实例个数的比值。完整的排序损失函数为 则标签排序损失 RL(M)为标签完备下的排序损失与标签非完备情况下的排序损失和,即 通过融合流型正则、排序正则与式(1),并通过惩罚法转化有约束优化问题为无约束优化问题,获得如下形式的目标函数 其中,λ1和λ2用于控制相关部分的权值。 在目标函数式(2) 中,部分项g(M)=和 RL(M)是非连续不规则函数,其导函数是间断函数,这使目标函数不具备精确解。同时,目标函数中的核范数||M||*与二次项的和可用高效算法来优化[24]。针对上述特点,本节借鉴ADMM 的可分性,将目标函数中核范数||M||*与二次项组合,并与剩余项分割开,利用文献[24]算法来优化核范数部分。对于剩余项,本节利用线性近似法求解其近似解。上述方法融合了近似法与传统 ADMM[1],本文称之为线性LADMM,其详细过程如下。 首先,引入辅助变量M=Z,将变量M的优化问题转化为变量M和Z的优化问题,其目标函数为 其次,转化式(3)问题为如下增广拉格朗日形式 其中,β是正的乘子参数,γ∈Rd×l是正的拉格朗日常数。本节算法包含三部分:更新M、更新Z、更新γ。 固定式(4)问题中的变量Z和γ,式(4)问题变为求解变M的最小化问题 式(5)问题包含非连续的不规则项g(M)和RL(M),其不具备精确解。本文利用二次近似法优化该问题从而获得任意程度的近似解。具体地,选取初始点M(0),对2 个项g(M)和 RL(M)在初始点展开为二次近似形式,展开后的函数是良定形式,求其精确解。以精确解为新的展开点重复上述过程直到获得任意近似程度的解。函数g(M)和RL(M)在近似点M(k)的近似展开形式为 求函数关于变量M的导函数,并设置导函数为0,可得 通过分析发现,Q1和2XXT是2 个对称矩阵,其对称分解为Q1=UAUT和2XXT=VBVT。其中U和V是特征向量,A和B是对角矩阵,对角线元素是Q1和2XXT的特征值。利用对称分解替换式(6)中的Q1和2XXT,可得 对式(7)左右两边分别乘以UT和V,可将其化简为 固定式(4)问题中变量M和γ,该问题变为求解变量Z的最小化问题,即 式(10)是最小化核范数问题,可用文献[24]算法来高效优化,其解为 固定式(4)问题中变量M和Z,变量γ可通过如下形式来更新 从式(6)可知,更新变量M需要计算变量Q1和Q2以及2XXT和Q1的对称分解,2XXT和Q1为常数矩阵,其计算和对称分解由预处理步骤处理。在计算Q2过程中,流型正则部分的导数为,其时间复杂度为O(ld2)。本节假设每个数据以均等概率标注标签和不标注标签,则排序正则部分的时间复杂度为O(l2n2d)。因此,更新变量M的时间复杂度为O(k(ld2+l2n2d+ld)),其中k是迭代次数。更新变量Z的时间复杂度为O(min{ld2,l2d})。更新变量γ的时间复杂度为O(ld)。 本文方案(简称为SLCR)单次循环时间复杂度为O((l2n2d+k(ld2+l2n2d+ld)+min {ld2,l2d}+ld)nk),其中,nk表示近似算法的迭代次数。BR 的时间复杂度为O(ld3+ldn2+d2n2+d3)。文献[7]方案(简称为WSABIE)采用批量梯度下降法优化目标函数,其时间复杂度为O(n s(ld+l2)),其中,ns表示单次选取的梯度下降数据数。文献[6]方案(简称为LEML)使用交替下降法优化目标函数,其单次循环时间复杂度为O(nnz(Y)+nnz(X))k+(n+l)k2),其中,nnz(Y)≪nL,k表示拟合矩阵的秩。文献[14]方案(简称为SLRM)采用交替下降法优化目标函数,其单次循环时间复杂度为O(d2nl+dn2+ldnl+min{dl2,d2l}+dl),其中,nl表示训练集中标记标签数据个数。文献[25]方案(简称为ICVL)采用交替下降法优化目标函数,其单次循环时间复杂度为O(l2n+d2n+d3+l3+ldn),其中,n表示实例个数,l表示标签个数,d表示特征维数。如上所述,本文方案时间复杂度高于对比方案时间复杂度。 本节在6 个经典的多标签数据集上比较本文方案和代表性标签缺失下的多标签学习方案的预测效果。 本文实验的数据集为Emotions、Scene、Birds、Mediamill、Delicious、NUS-WIDE-B。为有效检测标签缺失下模型的预测效果,本文剔除了未标记标签的数据,其详细统计信息如表1 所示。 表1 实验数据统计信息 为证明本文方案的预测效果,本节实验与如下代表性的标签缺失下的多标签学习方案进行比较:BR、WSABIE、LEML、SLRM、ICVL。本节使用Hamming Loss、Recall、F1-Measure、F1 macro、F1 micro 等5 个标准来评估各方案的预测效果。详细评估标准信息如文献[26]所示。 本文方案与对比方案在6 个数据集上的预测效果如表2~表6 所示。在5 个实验评估标准中,Hamming Loss 取值越小其方案效果越好,其余评估标准取值越大方案效果越好。为准确比较方案的实验效果,本文从大量实验结果中挑选了具有相似Hamming Loss 值的实验结果。从表2~表6 可以看出,本文方案获得了较好的预测效果。例如,在数据集 NUS-WIDE-B 上,本文方案在 Recall、F1-Measure、F1 macro、F1 micro 评估标准上比最好对比方案分别高0.073、0.075、0.057 和0.042。该结果证明了本文方案在处理缺失标签情况下更具稳定性。详细分析如下。 表2 6 个数据集上的Hamming Loss 比较 表3 6 个数据集上的Recall 比较 表4 6 个数据集上的F1-Measure 比较 表5 6 个数据集上的F1 macro 比较 表6 6 个数据集上的F1 micro 比较 1) LEML、SLRM 和ICVL 直接或间接考虑了低秩结构来提升预测精度,WSABIE 使用标签排序来约束目标函数。然而,本文方案比LEML、SLRM和ICVL 有更好的实验效果,其原因是低秩结构俘获了标签整体结构上的关联,标签排序和流型正则俘获了个体标签间的关联,2 种标签关联相互补充,从而获得了较好的预测效果。 2) 在Recall、F1-Measure、F1 macro 和F1 micro等评估标准下,BR 实验效果与WSABIE、LEML和SLRM 的实验效果接近。该结果证明了低秩结构在某些数据中并不总是有效。同时,本文方案在Scene 和Delicious 上取得了总体优于对比方案的实验效果,间接证明了流型正则化和排序正则化俘获了更有效的标签关联。 不同标签缺失率下本文方案与对比方案的预测效果如图3~图7 所示。该实验在5 个数据集Emotions、Scene、Birds、Mediamill 和NUS-WIDE-B 上进行。从图3~图7 可以看出,尽管本文方案的实验效果随着标签缺失率下降而下降,但是本文方案相比于对比方案仍获得较好的实验效果。其原因是本文流型结构从标签正实例出发来度量标签关联,避免了使用标签向量度量标签关联带来的偏差问题。同时,排序正则化在一定程度上缓解了标签错误标记带来的模型偏差。 图3 Mediamill 数据集上预测效果对比 图4 Emotions 数据集上预测效果对比 图5 Birds 数据集上预测效果对比 图6 Scene 数据集上预测效果对比 图7 NUS-WIDE-B 数据集上预测效果对比 本文针对标签缺失下的多标签标记问题,从数据流型角度出发俘获了标签关联,利用加权排序降低了模型偏差,并利用低秩结构正则化模型,从而有效填充了缺失标签。具体地,通过确保数据标签几何相似度与标签预测距离一致性俘获数据流型结构;通过度量完备标签下和不完备标签下的排序损失来对模型进行正则。实验结果表明,本文方案优于现有标签缺失下的多标签学习方案。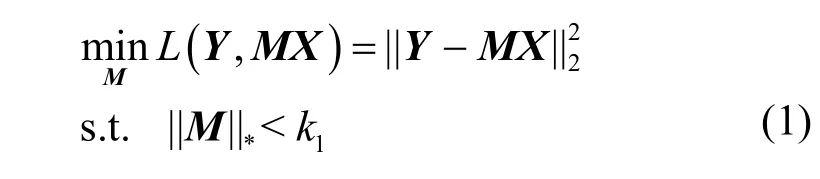
3.4 流型正则





3.5 排序正则
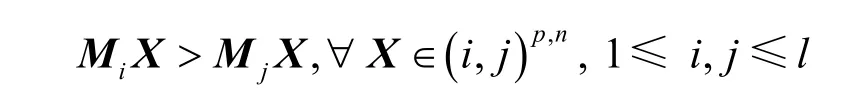
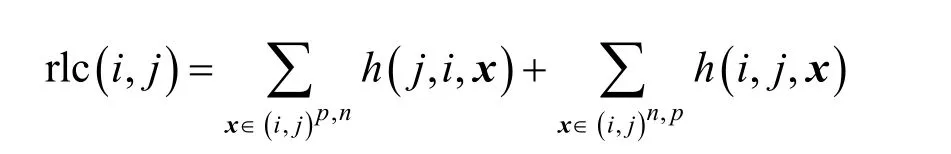
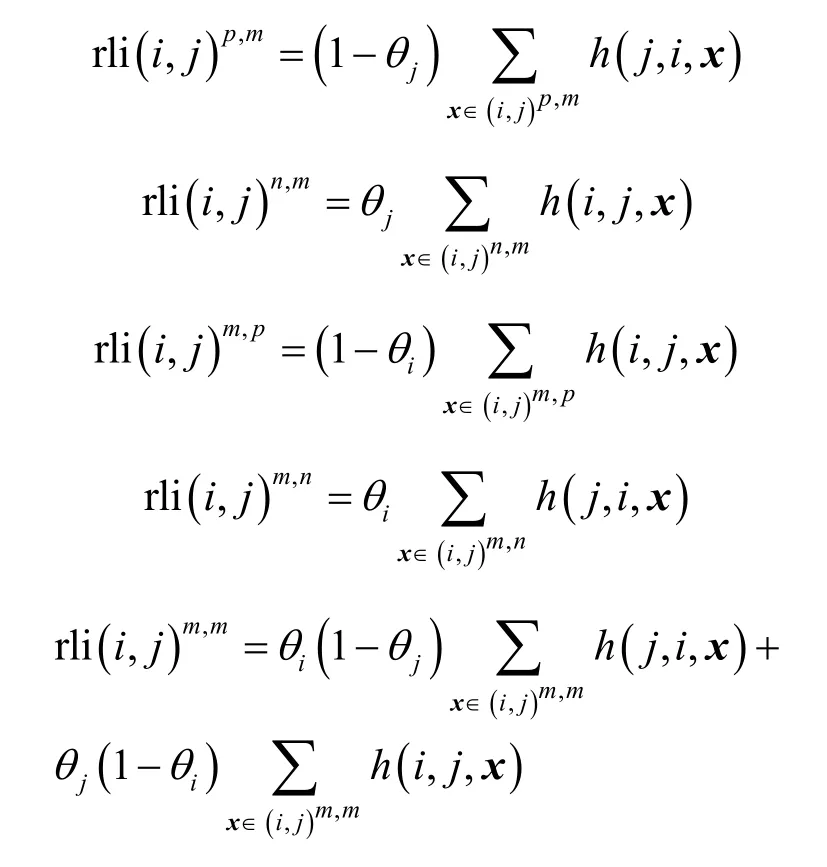
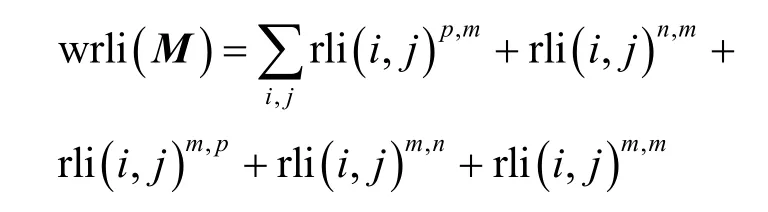
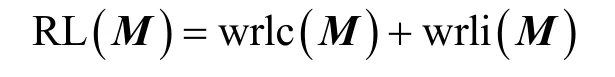
3.6 目标函数

4 模型优化
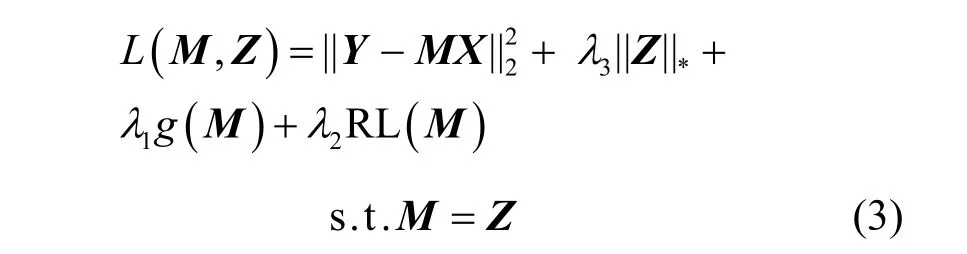
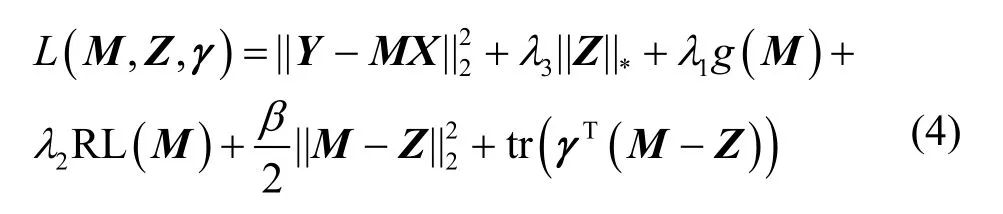
4.1 更新M

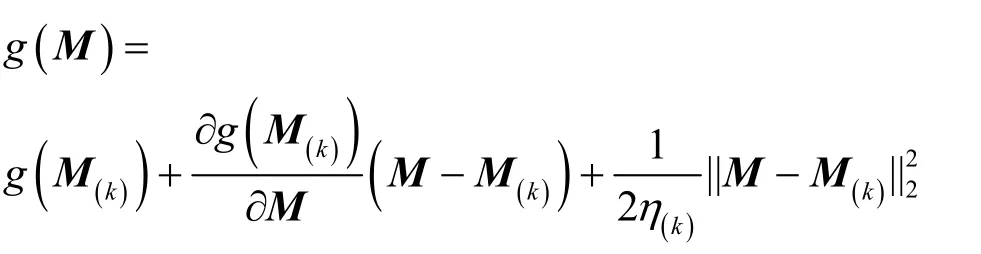

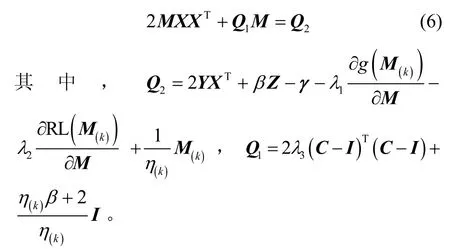
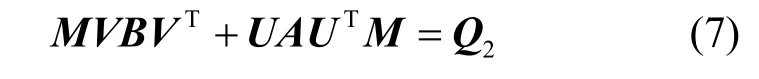


4.2 更新Z
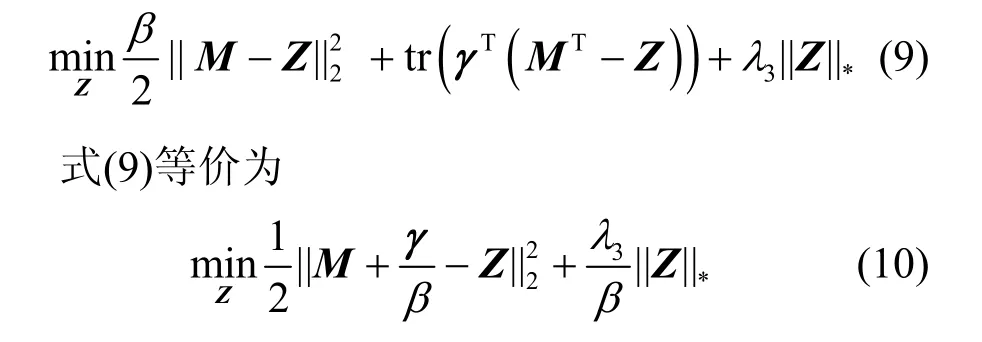

4.3 更新γ

4.4 复杂度分析
5 实验
5.1 数据集
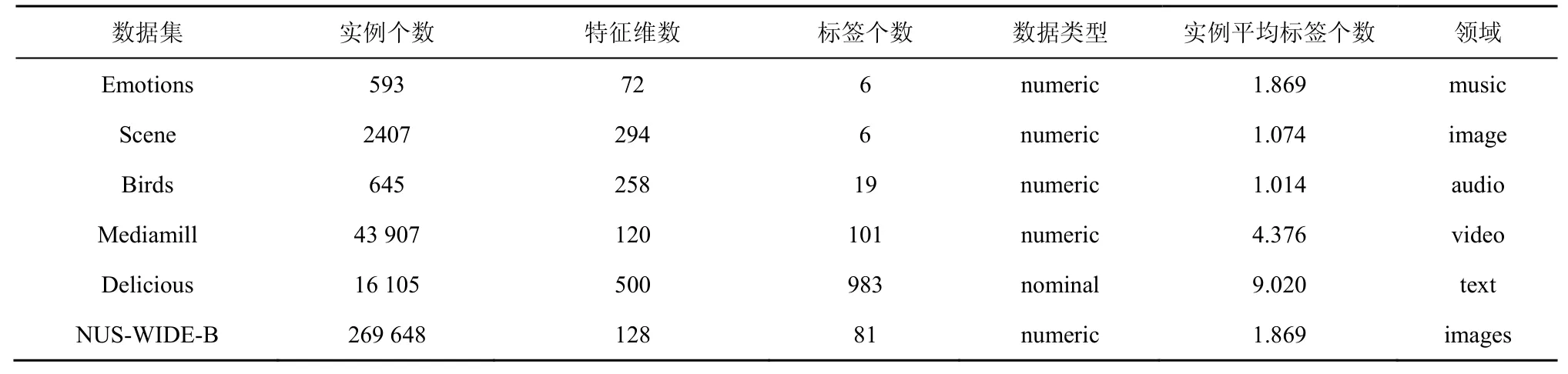
5.2 对比方案
5.3 实验结果
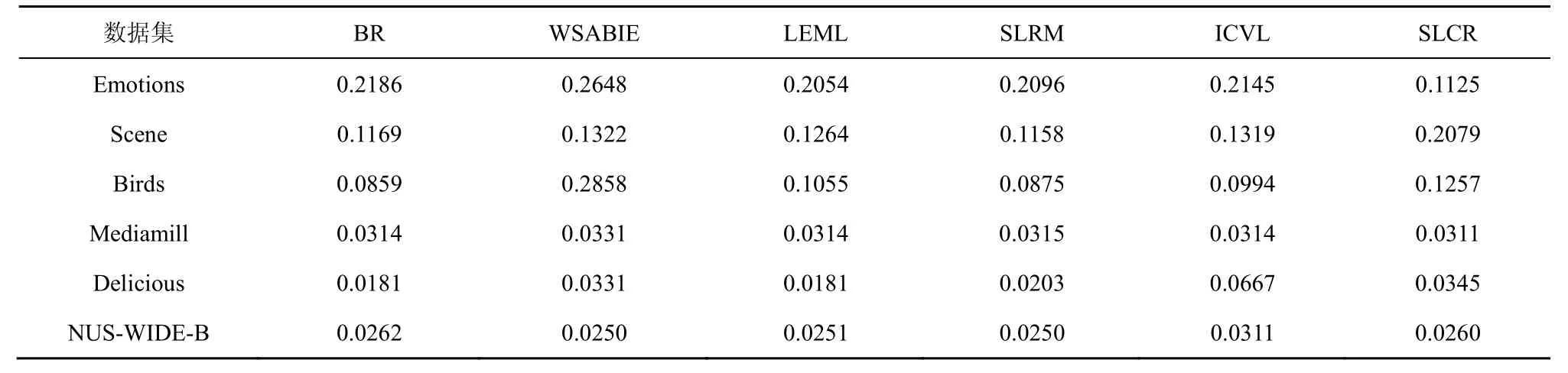


6 结束语
