短波频段高压输电线路的电磁散射场及其影响因子

2021-12-08杨晓峰唐波张建功赵志斌谢黄海刘钢

南方电网技术 2021年10期

杨晓峰，唐波,2，张建功，赵志斌，谢黄海，刘钢

(1.三峡大学电气与新能源学院，湖北宜昌443002；2.湖北省输电线路工程技术研究中心，湖北宜昌443002；3.中国电力科学研究院，武汉430074；4.华北电力大学电气与电子工程学院，北京102206)

0 引言

高压输电线路电压等级高、输送容量大、空间覆盖广，其架设运行会对邻近的无线台站产生无源干扰[1]。然而在我国土地空间日益紧张的背景下，当前只能依靠电磁散射场强空间自然衰减的特性，采取确定防护间距的办法解决无源干扰问题，这显然过于被动。因此，明确无源干扰的决定性影响因子，从而针对性进行线路改型，对有效解决高压输电线路与无线台站的电磁兼容问题具有重要意义。

国外对中波频段输电线路无源干扰防护措施及其影响因子进行了较为深入的研究，认为感应电流的二次辐射是造成干扰的根本原因[2]；同时干扰的变化特征存在谐振现象，因此破坏谐振产生条件是无源干扰防护的有效方法[3]。IEEE由此制定的标准认为，当干扰谐振现象发生时，将在单基铁塔[4]，或者在输电铁塔与地线组成的“环形天线”回路中产生幅值较大的感应电流，相应产生强烈的二次辐射场[5]。由于已建设好的铁塔结构无法改变，但可以通过“解谐器”[6]阻断“环形天线”回路以减小感应电流的方法破坏谐振发生的条件，从而减小干扰。

但是，这些研究仅针对中波频段的无源干扰而言。文献[7]对调幅广播收音台工作频段(0.526～26.1 MHz)的无源干扰进行了研究，发现在有无地线两种情况下，干扰极值及极值出现的频率均基本一致，这说明在短波频段，“环形天线”回路，即塔高和地线组成回路感应电流不再是干扰的决定性影响因子。文献[8]通过进一步的研究发现，当频率达到短波及以上时，无源干扰主要受输电线路地面以上金属结构对电磁波散射的影响。因此，对于短波频段的无源干扰影响因子，还需进一步探讨。

为此，本文从高压输电线路本体结构特征出发，详细分析了线路地线、线路档距、铁塔数量及铁塔高度等因素对感应电流的分布影响，从而间接确定输电线路电磁散射场的影响因子，为输电线路电磁干扰抑制提供理论参考。

1 高压输电线路无源干扰与抑制

1.1 高压输电线路的无源干扰

高压输电线路对邻近无线台站电磁干扰示意图如图1所示。高压输电线路主要由导线、地线、绝缘子串、线路金具、铁塔、铁塔基础以及接地装置等部分组成，其暴露在地表面以上的金属部分主要是铁塔、导线和地线[9]。从电磁学观点看，输电线路的铁塔、导线和地线可以看成是无数带电粒子的集合，各无线台站发出的入射电磁波与输电线路暴露在地面以上的金属部分中的带电粒子相互作用，产生新的等效电荷、电流，或者说产生了新的场源。随着入射电磁场的交变影响，输电线路各个金属导体部分产生的感应电流也是交变的，并在线路附近的空间产生新的电磁场，即所谓的二次散射场[10]。因此，输电线路金属部件属于二次散射体，它们自身不是激励源，由外部电磁场激励产生再散射。

图1 输电线路对邻近无线台站电磁干扰示意图

输电线路电磁散射产生的电磁波与原入射电磁波叠加，改变了原入射电磁波的幅值和相位，从而对无线台站发射或接收信号产生干扰，造成无线电测量误差。而输电线路电磁散射场强度的大小，取决于激励场的强弱和导体本身的物理属性，对于高压输电线路而言主要取决于输电线路的本体结构特征[11]。

1.2 无源干扰的抑制

目前解决高压输电线路对邻近无线台站无源干扰问题的主要方法是，根据国家现行的不同无线台站电磁环境防护标准提出防护间距，进而要求高压输电线路绕行于台站的防护间距之外[12]。如果输电线路与台站之间的距离小于标准规定的防护间距，则需要改变输电线路的路径，让线路以台站为中心更大的半径绕行，以满足防护要求，这无疑将造成严重的经济损失，甚至于线路无法建设。因此，这种单纯依托于电磁场空间距离衰减的防护措施是一种被动的方法。

这种依靠距离规定的被动防护方法不但对实际工程建设带来了困难，还无法解决已建设存在的线路与台站之间由于距离不够而产生的干扰问题。因此，IEEE提出了改变输电线路谐振频率的方法，通过“避让频率”的方式以主动抑制输电线路对邻近无线台站的电磁散射场[13]。其核心思想是，在激励电磁波作用下，输电铁塔可等效成如图2(a)所示的竖直于地面的线天线，输电线路则可根据档距形成多个如图2(b)所示的“环形天线”。

针对于图2(a)竖直于地面的线天线，可根据半波天线理论，认为当铁塔高度达到λ/4(λ为波长)时，铁塔及其大地镜像形成了半波天线，交变电磁场在垂直于地面的铁塔中产生的感应电动势达到最大，相应的铁塔表面的感应电流也达到最大。此时，感应电流产生的二次辐射场最强，对无线台站的无源干扰也最为严重。

当输电铁塔与地线未绝缘时，地线将1个档距内相邻的2基输电铁塔连接起来，与其对地镜像形成如图2(b)所示的“环形天线”。根据“环形天线”的辐射特性，当“环形天线”的长度为无线台站发射的电磁波波长的整数倍时，将发生谐振现象，回路中出现感应电流峰值，从而造成二次辐射产生峰值，干扰也出现相应的极大值。

图2 输电铁塔线天线及输电线路环形天线示意图

因此，当前的诸多无源干扰研究试图预测输电线路无源干扰的谐振频率，从而通过避开干扰谐振，或者破坏谐振条件，从而限制输电线路的感应电流，以此减小输电线路的电磁散射场以减小干扰。然而文献[7]发现随着电磁波频率的增加，尤其是当频率达到短波及以上频段时，铁塔细节的电尺寸效应相对于波长的缩小而逐步变得不可忽略，这也是IEEE标准也将这些结论限定为中波频段，而且最好是1.7 MHz以下。

综上所述，当前所明确的无源干扰决定性影响因子，以及针对性减小感应电流以抑制干扰的方法，适用于中长波频段，而对于工作在短波频段，乃至更高频段的无线台站并不适用。因此，对于短波频段的无源干扰的感应电流分布，还需结合输电线路本体结构特征进一步探讨。

2 输电线路的电磁散射场求解

2.1 无源干扰的电场积分方程与感应电流

输电线路对邻近无线台站产生无源干扰的数学模型如图3所示。图3中包含直角坐标系(x，y，z)和球坐标系(r，θ，φ)。假设输电线路为理想导体V，输电铁塔沿x轴以一定档距均匀排列，电磁波Ei入射输电线路的角度为(θi，φi)，J(r′)为输电线路上任意一点r′处的感应电流密度，会向空间进行二次辐射，Es为无线电接收台站所在场点r处的电磁散射场。

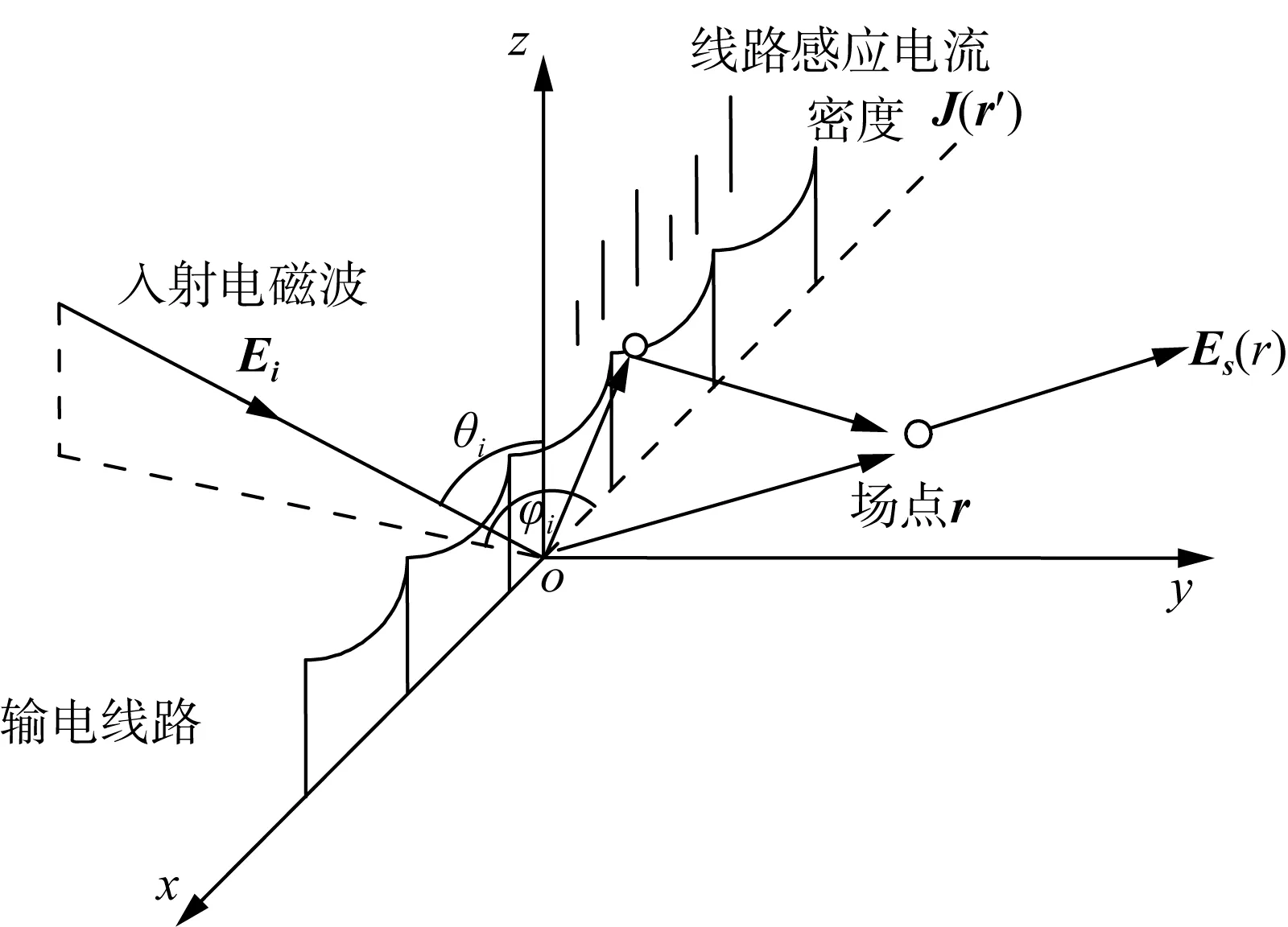
图3 输电线路电磁散射场求解数学模型

由电磁场理论可知，各无线电台站所发射的入射电磁波(激励场)将在输电线路的金属部件表面产生与激励场强呈正相关性的感应电动势，此感应电动势在金属表面激励出交变的感应电流[14]。根据金属导体的趋肤效应可知，感应电流主要集中在导体表面。之后，集中在导体表面的感应电流将作为新的激励源，向外部空间发射与激励场同频的散射场，也就是二次辐射场，对输电线路邻近的无线台站产生干扰。

文献[15]结合基于上述电磁散射机理，根据电磁波波长与目标散射体之间的电尺寸比例关系，对于短波频段输电线路无源干扰的求解构建了铁塔三维面模型和地线线模型相组合的线-面混合模型，并给出了模型求解用线、面电场积分方程和基于感应电流离散的求解算法。经与北京康西草原的线路缩比模型实验数据的对比分析，该数学模型和算法具有较好的准确性[16]。

利用线模型计算输电线路的无源干扰时采用相应的线电场积分方程：

(1)

式中：l为沿细导线轴线方向的单位矢量；Ei(r)为入射电磁波电场强度；ω为入射电磁波角频率；μ为磁导率；ε为介电常数；g(r,r′(l′))为格林函数；l′为铁塔线模型的线积分区域；I(l′)为细导线轴线方向的线电流密度，I(l′)=2πaJ(l′)；a为线模型的等效半径。

利用面模型计算输电线路的无源干扰时，需要采用相应的面电场积分方程：

(2)

输电线路线-面模型上离散感应电流的求解可根据矩量法原理，首先采用适当的基函数对线-面模型上的感应电流进行离散，离散后基函数的展开系数即为各个对应离散单元上的感应电流。式(3)给出了输电线路金属构件表面分布的感应电流表达式。

(3)

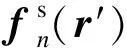
获得用基函数表示的感应电流后，将其代入公式(1)和(2)的电场积分方程中，并根据等式变换得到差值函数；之后利用适当的检验函数与差值函数联立，得到关于基函数展开系数的矩阵方程组。

(4)

式中：等号左侧的阻抗矩阵由9个元素组成，Zss为三角面元自作用阻抗；Zww为线单元的自作用阻抗；Zjj为线面连接点自作用阻抗；Zsw和Zws为三角面元和线单元相互作用阻抗；Zsj和Zjs为三角面元和线面连接点的相互作用阻抗；Zwj和Zjw为线单元和线面连接点的相互作用阻抗；Is为面模型上的感应电流；Iw为线模型上的感应电流；Ij为线面连接点处的感应电流；等号右侧为电压矩阵，Vs为面模型上的感应电压；Vw为线模型上的感应电压；Vj为线面连接点处的感应电压。

最后，通过求解式(4)得到感应电流基函数的展开系数组，即Is、Iw和Ij，也就得到了整个线面模型中的感应电流分布J(r′)，最后求解得到测点处的电磁散射场。

2.2 输电线路的感应电流分布特点

输电线路线-面模型的感应电流直接影响了输电线路电磁散射场的分布，因此通过分析输电线路线-面模型上感应电流的变化，即可间接反映出输电线路电磁散射场的变化。

为研究输电线路线-面模型上感应电流的影响因素，对感应电流的求解式(4)进行分析。式(4)中，等号右侧为电压矩阵是已知量，其值取决于入射电磁波的幅值、入射角度和频率。等号左侧为输电线路阻抗矩阵和待求的感应电流矩阵，根据阻抗矩阵的元素组成可知，其与输电线路的本体结构特征密切相关。以与输电铁塔面模型结构特征有关的Zss为例，有：

(5)

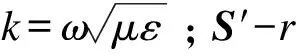
式(5)中的积分域实际上就是输电铁塔的金属表面，也即感应电流分布的区域。当铁塔高度、结构或者铁塔数量发生变化时，Zss元素求解的积分域必然发生改变，从而导致求解得到的Zss元素存在差异。

同理可知，Zww取决于线路地线线模型的结构特征，当地线数量、地线长度(线路档距)发生变化时必然导致Zww元素求解的积分域发生变化，进而导致求解得到的Zww元素存在差异；而Zsw和Zws、Zsj和Zjs以及Zwj和Zjw等元素则与输电铁塔与地线连接情况有关，当铁塔数量发生变化时，将引起线模型与面模型连接点数量的变化，进而使阻抗矩阵发生变化。

综上所述，感应电流矩阵的求解，直接受输电线路阻抗矩阵的影响，而输电线路阻抗矩阵中的各元素又与线路地线、线路档距、铁塔数量、铁塔高度等本体结构特征密切相关。当输电线路本体结构特征发生变化时，必然会导致输电线路上感应电流分布发生改变，进而引起观测点处电磁散射场的变化。

3 电磁散射场的影响因子响应分析

以±800 kV向家坝—上海高压特高压直流输电线路为例，对输电线路地线、线路档距、铁塔高度及铁塔数量等发生变化时的输电线路的感应电流和散射场强进行分析，探讨输电线路的各种本体特征对散射电场的影响程度。

3.1 输电线路地线的响应特性

以±800 kV向家坝—上海特高压直流输电线路ZP30101型铁塔实际尺寸为例，建立输电线路无源干扰求解的线-面混合模型如图4所示。

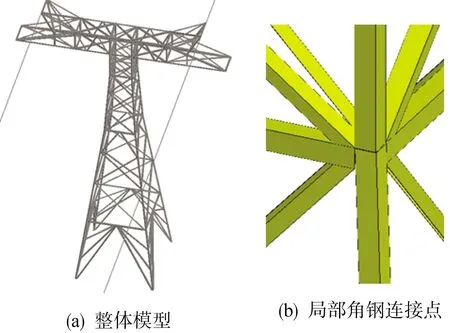
图4 特高压直流ZP30101 型铁塔线-面模型

线路铁塔高63 m，横担宽42.2 m。导线采用6×ACSR-720/50钢芯铝绞线，导线外径为36.24 mm，分裂间隔为450 mm。根据标准[17]，对分裂导线用半径0.355 1 m的单根等效导线代替。铁塔与双地线连接，地线型号LBGJ-180-20AC，该型地线直径为17.5 mm，两根地线相距32.4 m，弧垂13 m。

考虑到短波频率电磁波波长以10 m为单位量级，远小于线路与无线电台站之间以千米为单位的间距，因此各类无线台站对输电线路的激励电磁波为平面波。同时铁塔竖直于地面，因此采用干扰最严重的垂直极化平面波进行激励，其电场强度为1 V/m。根据文献[8]，输电线路无线电干扰测量天线在地面2 m高处，观测场点距离输电线路中心线的垂直距离为2 000 m，因此取观测点坐标为(0，2 000，2)。输电线路与观测点相关位置如图5所示。

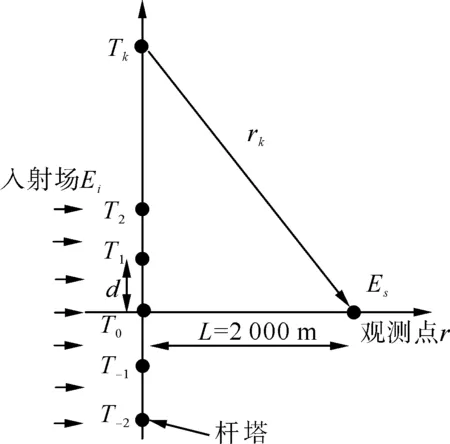
图5 输电线路与观测点相关位置布置图

根据第2节的分析可知，输电线路的无源干扰受输电线路地面以上金属结构对电磁波散射的影响，即主要受输电铁塔表面分布的感应电流影响。

因此，为研究短波频段输电线路地线对电磁散射场的影响，控制线路档距、铁塔数量和铁塔高度等因素保持不变，分别对不架设地线、架设单根地线和架设双根地线等情况下输电铁塔表面的感应电流和观测点处的电场强度进行仿真求解。求解得到10 MHz和20 MHz不同短波频率下，输电铁塔表面的感应电流最大幅值和观测点处的电场强度随线路地线的变化情况分别如图6(a)和(b)所示。

图6(a)中，对于10 MHz频段，输电铁塔表面的感应电流在不架设地线时最小，其最小值为244.51 mA/m；架设双根地线时输电铁塔表面的感应电流最大，最大值为248.34 mA/m，地线变化时感应电流的最大差值为1.5%。而对于图6(b)所示的20 MHz频段，地线变化时感应电流的最大差值更小，仅为0.53%。若分析观测点处电场强度的变化，10 MHz和20 MHz时有无地线的场强最大差值分别为0.46%和0.048%。这些结果表明，在短波频段地线与铁塔绝缘与否对输电铁塔表面的感应电流影响不大，且随频率增加地线对干扰的影响逐步变得更小。该规律与文献[7]研究结论一致。

图6 线路地线对输电感应电流和电磁散射场的影响

另外，从图6可以看出，观测点处散射电场和输电铁塔表面的感应电流随线路地线变化的趋势一致，这进一步说明了输电线路电磁散射场主要受铁塔表面的感应电流影响。

3.2 输电线路档距(铁塔数量)的响应特性

输电线路的档距和铁塔数量其实是同一类影响因子。在线路长度一定时，档距越大，铁塔的数量越少，反之亦然。因此，为一进步研究输电线路档距是否是输电线路电磁散射场决定性影响因子，控制线路地线及铁塔高度等因素保持不变，并控制线路总长度为1 500 m，分别求解线路档距为300 m(对应6基塔)、375 m(对应5基塔)，以及500 m(对应4基塔)3种情况下输电铁塔表面的感应电流和观测点处的电场强度。最后将求解得到10 MHz和20 MHz不同短波频率下，输电铁塔表面的感应电流最大幅值和观测点处的电场强度分别如图7(a)和(b)所示。

图7 线路档距对输电感应电流和电磁散射场的影响

从图7可以看出，观测点处散射电场和输电铁塔表面的感应电流随输电线路档距变化的趋势一致，且随档距增大而减小。图7(a)中，在10 MHz频段，输电铁塔表面的感应电流在档距为500 m时最小，其最小值为1 764 mA/m；档距为300 m时感应电流最大，最大值为2 234 mA/m，档距变化时感应电流的最大差值为21.0%；而对于图7(b)所示的20 MHz频段，档距变化时感应电流的最大差值为20.9%。若分析观测点处电场强度的变化，10 MHz和20 MHz频段在档距变化时观测点处电场强度变化的最大差值分别为6.3%和14.4%。这些结果表明，短波频段的线路档距对输电铁塔表面的感应电流和散射电场影响较大。

3.3 输电线路铁塔高度的响应特性

为一进步研究铁塔高度是否是输电线路电磁散射场决定性影响因子，控制线路地线、线路档距以及铁塔数量等因素保持不变，分别求解铁塔高度为63 m、73 m、83 m以及93 m 4种情况下输电铁塔表面的感应电流。最后将求解得到10 MHz和20 MHz不同短波频率下，输电铁塔表面的感应电流最大幅值和观测点处的电场强度分别如图8(a)和(b)所示。

从图8(a)中可以看出，对于10 MHz频段，输电铁塔表面的感应电流在铁塔高度为93 m时最小，其最小值为1 821 mA/m；铁塔高度为63 m时，输电铁塔表面的感应电流最大，最大值为2 236 mA/m，铁塔高度变化时感应电流的最大差值为18.6%；而对于图8(b)所示的20 MHz频段，铁塔高度变化时感应电流的最大差值为15.8%。若分析观测点处电场强度的变化，10 MHz和20 MHz频段铁塔高度变化时观测点处电场强度变化的最大差值分别为14.5%和11.6%。这些结果表明，在短波频段地铁塔高度对输电铁塔表面的感应电流和散射电场影响较大。

图8 铁塔高度对输电感应电流和电磁散射场的影响

从图8整体来看，观测点处散射电场和输电铁塔表面的感应电流随铁塔高度变化的趋势仍然一致，但随铁塔高度增加而减小。这种变化可以考虑对输电线路而言，铁塔塔头辅材较多、结构复杂，是输电线路无源干扰的主要电磁散射体。特别针对于直流线路铁塔只有一个横担的情况，当铁塔高度增加时，实际上是增加了铁塔呼称高度(即铁塔下横担下边缘与地面间的距离)，根据几何关系可知铁塔塔头与观测点之间的距离将增大；再加上铁塔呼称高度增加导致电磁波直接穿过塔身到达观测点，使得铁塔塔头对观测点处的电磁散射减弱，以上原因最终导致观测点处的场强减小。

为进一步研究铁塔塔头复杂金属结构体对电磁波的遮挡和散射效应，降低铁塔呼称高度以正好遮挡住观测点，这样以测点高度2 m为中心设定塔头高度变化范围。如图9所示，分别计算10 MHz频段下铁塔呼称高度为0.5 m、1 m、1.5 m、2 m、3 m、4 m，以及5 m高度时观测点处的电场强度，以此研究塔头对观测点的电磁波遮挡和散射影响，计算结果如图10所示。需要注意的是，由于铁塔横担高度为4.6 m，呼称高度小于2 m时，均属于铁塔横担遮挡观测点的情况(此时电磁波不是直接穿越塔身到达观测点)，因此在2 m以下额外以0.5 m为间隔进行计算分析，从而进一步研究在遮挡情况下增加呼称高度对观测点处场强的影响。

图9 观测点与横担相对位置示意图

图10 观测点处电场强度随呼称高度变化

需要指出的是，上述塔高范围虽然在实际工程中不存在，但从图10中可以看出，当铁塔呼称高度为1 m时，即电磁波正好被塔头遮挡时，观测点处电场强度达到最大，而其他高度则随着塔头对电磁波的遮挡面积减小，场强而逐渐减小，仿真结果与理论分析一致。因此，可以认为铁塔塔头主材、辅材连接复杂，金属角钢众多，是铁塔对观测点进行二次辐射的主要部位；随着铁塔高度的增加，塔头距观测点的距离增大，电磁波直接穿过金属角钢不多、遮挡较少的塔身，而铁塔塔头这一主要的电磁散射体对观测点处的二次辐射减弱，导致观测点处的场强减小。