采用周期边界条件计算高压交流输电杆塔周围电场的简化方法
2021-12-08侯树政田蔚光邹军刘培杰
侯树政,田蔚光,邹军,刘培杰
(1.电力系统及发电设备控制和仿真国家重点实验室(清华大学电机系),北京100084;2.国网经济技术研究院有限公司,北京102209)
0 引言
对输电线路周围的电场已有较多研究,可采用二维模型计算无限长直输电线路在空间产生的电场分布[1-5],但是当需要考虑导线弧垂、交叉跨越或转角时,就需要对输电线进行三维建模,求解该场景下的电场分布应用较多的是模拟电荷法(CSM)[6-10],然而这些文献中对有限长输电线进行分段后直接计算电荷,此时输电线两端悬空,则电荷将会在输电线两端聚集,这与实际情况不相符,并且对于多档输电线路,导线分段数量多,计算量大,不利于实际应用。因此若只求解多档输电线路中间某一区域电场,考虑输电线路的周期性结构,可采用周期边界条件将整个输电线路的影响归并到一档线路之内,则可消除输电线路端部效应,并且减少了待解未知数的数量,提高了计算效率。文献[11]将输电线两端等效为半无限长线电荷,但模拟电荷法的精度取决于模拟电荷的数量和布置方式,用一根线电荷代替远端延伸的导线,模拟电荷数量过少可能会导致结果误差增大[12]。
此外,若考虑输电杆塔对导线电荷和周围电场的影响,则需对输电杆塔进行建模[13-18],将输电杆塔简化后分为若干段有限长线电荷。此时输电线路的电荷不再均匀分布,输电线应做更细化分段,以保证计算结果准确性。输电线路以一档为一个周期单元,每档长度为400 m左右,档距较长,分段后的电荷数量太多,计算量远大于不考虑杆塔时求解输电线路电场问题,因此针对该场景的电场求解,需要一种更高效的计算方法。
针对考虑杆塔影响场景下,计算多档输电线路中杆塔周围区域电场问题,本文提出一种使用周期边界条件计算输电线路电场的简化方法。先利用周期边界条件构造方程矩阵,然后将输电线路两侧距离杆塔较远的电荷用二维无限长输电线电荷替代,减少未知数和方程的个数,提高计算效率。求解方程矩阵得到受杆塔影响下的输电线路电荷分布和输电杆塔电荷后,对杆塔周围区域电场进行计算。
1 计算方法
首先说明利用周期边界条件求解输电线路和杆塔电荷的计算要点和过程,然后对其进行简化,减少计算量,提高计算效率。
1.1 周期边界条件计算方法
考虑杆塔的影响时,需要搭建三维输电线路和杆塔模型。设输电线长度为L,将其划分成M段有限长圆柱导体,匹配点选在输电线导体段表面,线电荷单元位于导体的中心轴线上。以导体棒左端为坐标原点,沿着导体棒的中心线建立坐标系,则第m段的中点的坐标为ym,如图1所示。
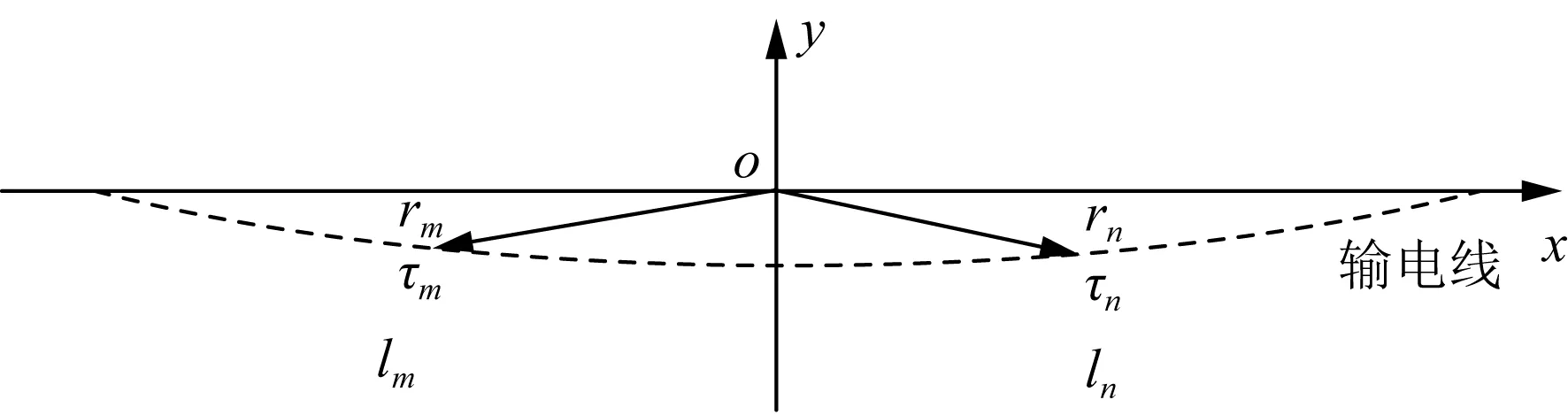
图1 输电线分段及坐标系示意图
线电荷在导体表面匹配点建立电位积分方程如下。
(1)
式中:rn和rm分别为场点和源点坐标;t(rm)为导体段线电荷密度;V0为输电线表面电位,因为输电线为工频交流电,所以电位用频域形式表示;G(rn,rm)为点电荷在无限大空间建立电位的格林函数;G为源点位置。
根据式(1)计算出每段导体表面的电位平均值,并做归一化处理,可将第n段上平均电位方程写成矩阵形式:
[P][σ]=[V]
(2)
式中:P为电位系数矩阵;σ为电荷向量;V为电位向量。则场点和源点之间归一化后的电位系数pmn如式(3)所示。
(3)
(4)
为场点和源点之间归一化后的电位系数;lm、ln分别为源点和场点导线分段的长度;σm为源点导线分段的总电荷,具体求解公式可参考[19-20]。
对输电杆塔可以用类似的建模方法,但由于杆塔的实际结构相当复杂,因此建模过程中不可能包含铁塔的所有部件,建模时对杆塔做如下简化[15-16]:
1)保留铁塔的主要金属构架,忽略绝缘子、均压环、金具等次要构架;
2)用圆柱导体代替铁架的金属角钢;
3)铁塔较长构架等效为多段直线段连接,每段直线段分别设置模拟线电荷;
4)有限长模拟线电荷设置在圆柱中心轴线上,匹配点选在圆柱表面。
将输电杆塔共分成N段,垂直导线方向为x轴,平行导线方向为y轴,垂直地面向上为z轴正方向,同塔双回鼓型塔的模拟电荷模型如图2所示。
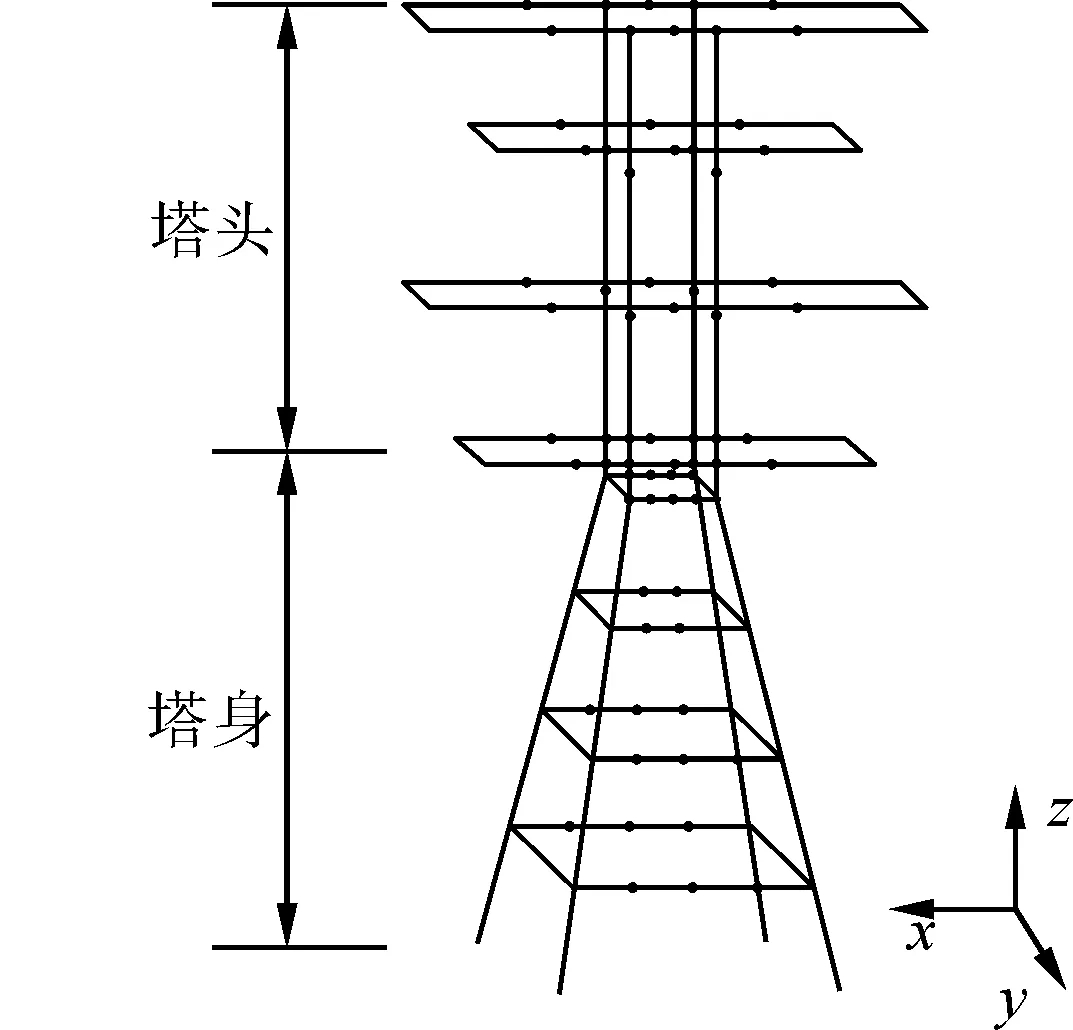
图2 输电杆塔模拟电荷模型示意图
输电线和杆塔之间存在相互影响,根据叠加原理,结合所有电位方程,列出电位求解方程矩阵形式如下:
(5)
式中:Ptt为杆塔对杆塔表面电位的作用;Ptc为输电线对杆塔表面电位的作用;Pct为杆塔对输电线表面电位的作用;Pcc为输电线对输电线表面电位的作用;σt为杆塔电荷;σc为输电线电荷;Vt为杆塔表面电位;Vc为输电线表面电位。
输电线路具有周期性结构,可将每档视作一个周期单元,因此可采用周期边界条件将整个输电线路的周期影响归并到一档线路之内,减少方程数目,消除端部效应。周期数越大,则计算的场景越接近无限长导体的电荷分布。
如图3所示的输电线路,将其分为3个单元,编号分别为#(-1)、#(0)、#(+1)。
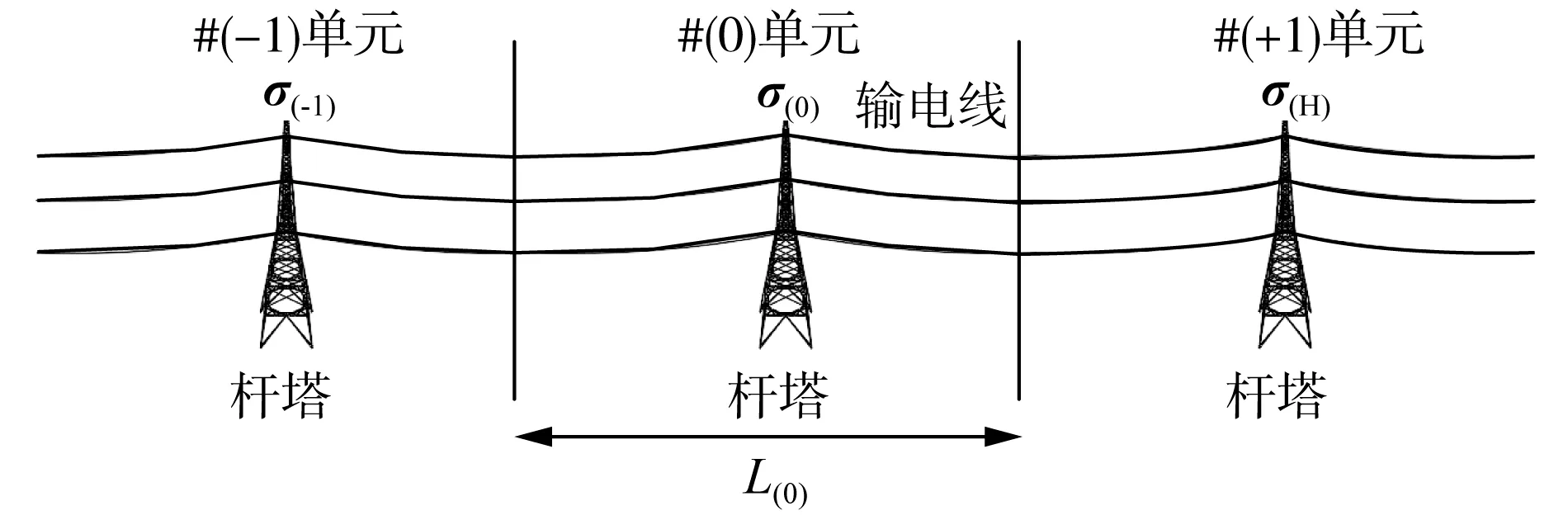
图3 多档高压输电线路周期结构示意图
计算#(0)单元内的电场,各单元内线电荷密度为
(6)
对整个输电线路按照式(2)列写电位方程,有
(7)
式中P(i)(j)为第(j)单元和第(i)单元之间的互电位系数矩阵,矩阵中元素按照式(3)计算。因为输电线电荷分布具有周期性,即
σ(-1)=σ(0)=σ(+1)
(8)
将电荷的周期关系代入方程矩阵中
[P(0)(-1)+P(0)(0)+P(0)(+1)][σ(0)]=[V(0)]
(9)
可见,使用周期边界条件可以降低方程数目,有效压缩计算量,但是输电线路以一个档距为周期,输电线路的档距平均为400 m,跨度较大,输电线分段较多,对于多回线路,未知量的求解个数增加迅速,计算量较大,不利于在实践中应用,因此需要对该方法进行简化,提高计算效率。
1.2 考虑杆塔时的简化计算方法
1.2.1 忽略杆塔对其他单元的影响
因为输电线路档距较大,所以不同单元内的输电杆塔相距很远,因此输电杆塔对其他单元内的杆塔和输电线影响可忽略不计,则输电杆塔上的线电荷可不参与周期变化,只有输电线的电荷需要使用周期条件来消除端部效应。因此#(0)单元内杆塔电荷单独计算,则式(7)可改写为
(10)
将各单元的电荷周期关系带入式(10),有
(11)
可将式(11)简写为
(12)
式中
Ptc=Pt(0)c(-1)+Pt(0)c(0)+Pt(0)c(+1)
(13)
Pcc=Pc(0)c(-1)+Pc(0)c(0)+Pc(0)c(+1)
(14)
表示输电线周期结构对#(0)单元内的作用。
1.2.2 确定杆塔对输电线电荷分布影响范围
此外,考虑杆塔对输电线上电荷分布的影响,认为杆塔只对其周围区域输电线电荷分布产生影响,则输电线距离杆塔较远部分的电荷受杆塔影响可忽略不计,因此确定杆塔对输电线电荷分布的影响范围后,可将输电线分为杆塔影响区域和非杆塔影响区域,位于非杆塔影响区域的输电线电荷则认为不受杆塔影响,应均匀分布,用无限长直输电线电荷替代,表示不受杆塔影响时,输电线的电荷分布,从而减少待求电荷的数量,降低计算量。
确定杆塔影响范围时,先利用二维模型计算出不考虑杆塔影响时,无限长直输电线上的线电荷大小,该电荷即为远离杆塔时输电线上均匀分布的电荷大小。再用考虑杆塔存在时的三维模型建立有限长输电线和杆塔的模型,将输电线每10 m一段划分成若干有限长圆柱,模拟电荷位于圆柱的轴线上,计算出此时输电线上的电荷分布,并和二维计算得到的电荷结果进行比较,不同电荷误差要求下,距离杆塔20 m采样线上的电位计算结果误差和计算时间如表1所示,综合考虑电位误差和计算时间,将电荷偏差超过1.5%的区域视作杆塔对输电线电荷分布的影响区域,周期单元内其余部分则视为非杆塔影响区域。因此,计算#(0)单元内电场时,将#(0)单元内输电线路分为3部分,σc也分为3部分,如图4所示,σc1,σc3表示非杆塔影响区域的输电线线电荷分布,σc2表示杆塔影响区域输电线线电荷分布,σt表示杆塔线电荷,单元内输电线长度为L。

表1 不同杆塔对电荷影响要求下计算结果对比
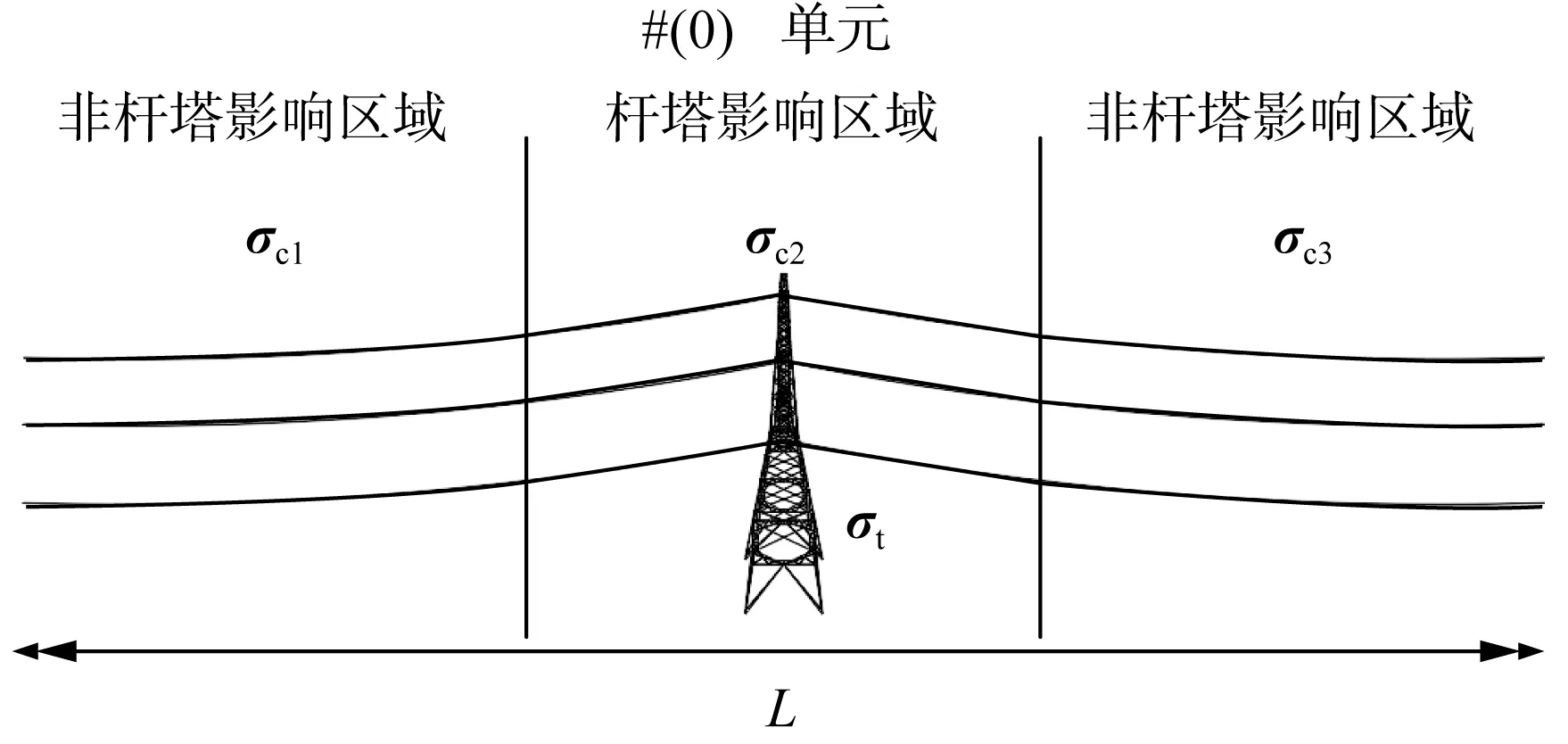
图4 #(0)单元内杆塔影响区域划分示意图
1.2.3 计算长输电线和杆塔电荷分布
确定了杆塔的影响范围后,对输电线进行较细化分段,σc拆分后可将式(12)改写为
(15)
然后将非杆塔影响区域的输电线上电荷用无限长直输电线电荷替代,可得
σc1=σc3=σ2D
(16)
式中σ2D为二维模型计算得到输电线电荷。将式(15)矩阵方程简化为
(17)
将待求解的方程矩阵维度降低,可减少计算量。求解矩阵方程即可得到杆塔周围输电线电荷分布和杆塔模型电荷,最后根据所得电荷计算出杆塔周围电场。
2 方法验证
2.1 解析算例:三相交流输电线电荷分布计算
以单回和双回输电线为例验证本文方法计算结果的准确性,图5为一组大地上方平行于地面放置的单回三相交流输电线,为方便解析计算忽略输电线弧垂,其距离地面的高度h=30 m;输电线半径r=0.01 m,各相之间距离d=6 m,输电线电压模值V=1 kV,相位互差120 °。图6为双回输电线路,两侧竖直排列,从上到下左侧为ABC相序,右侧为CBA相序,最下方输电线距地面高度h=30 m,两回输电线间距w=12 m,各相间距d=9 m。解析方法采用镜像法和电轴法计算输电线电荷[21]。

图5 单回输电线路架设几何结构示意图
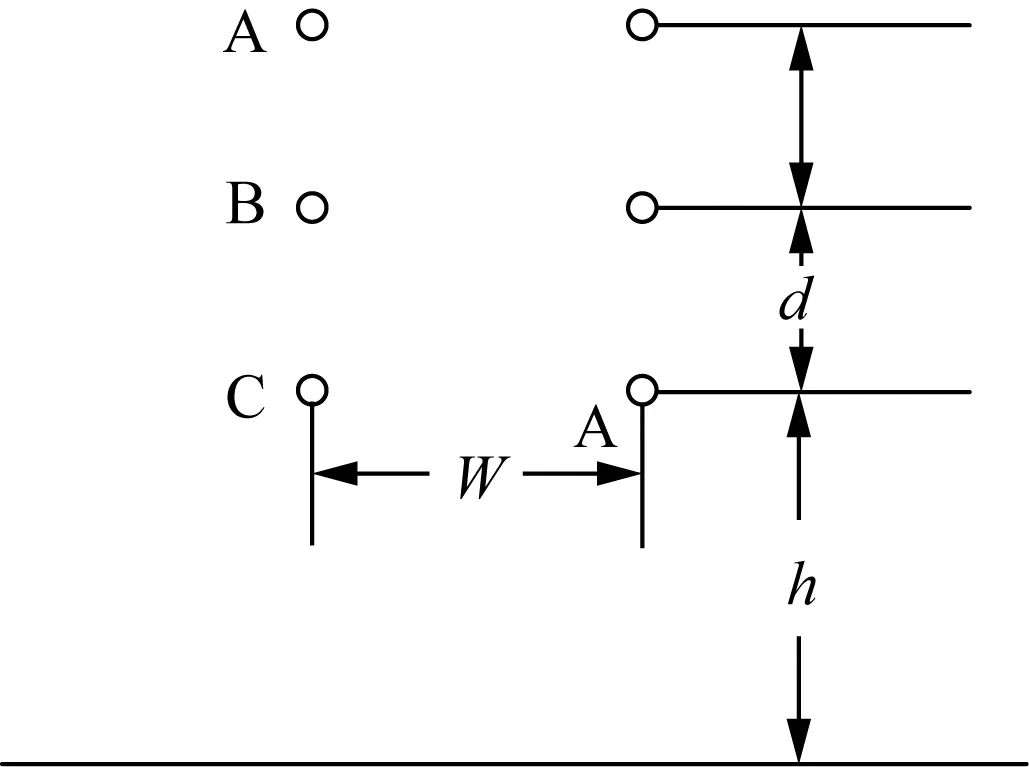
图6 双回输电线路架设几何结构示意图
设输电线总长度为1 200 m,整个输电线分为3个单元,每个单元400 m,各单元内输电线等长地分为40段,每段长10 m,分别利用式(9)、(17)计算中间单元输电线上电荷分布,比较原周期条件方法和本文简化方法计算结果与解析计算结果的误差,在本文简化方法中将中间单元输电线两端各100 m的部分用解析结果替代。两种方法计算得到的中间单元电荷模值分布误差如图7所示。

图7 不同计算方法输电线电荷误差比较
结果显示,计算单回输电线时,两种方法误差均为0.023 9%;计算双回输电线时,两种方法均为0.036 5%,说明本文方法计算结果足够准确,且本文简化方法中输电线两端电荷用解析结果替代,因此误差为0。
2.2 数值算例:同塔双回输电线电场计算
以330 kV同塔双回输电线路为例,共有6条导线和2条地线,杆塔影响范围为40 m,将导线和地线每5 m分一段,则每根导线和地线在杆塔影响区域分为8段,非杆塔影响区域分为72段,将输电杆塔分为56段导体,单元内导体总数为680段,图8为采样线示意图。

图8 330 kV交流输电线采样路径俯视图
为进行计算结果对比,以杆塔底部中心位置为坐标原点,平行于输电线的水平方向为y轴,垂直于输电线的水平方向为x轴,z轴垂直于地面,向上为正方向建立三维坐标系。过a(-20,0,20)、b(-15,0,20)、c(-10,0,20)3点分别做平行于y轴,长40 m的采样线,此时两种方法电位计算结果误差如图9(a)所示;再分别过d(0,20,20)、e(0,15,20)、f(0,10,20)3点做平行于x轴,长40 m的采样线,此时两种方法电位计算误差如图9(b)所示。
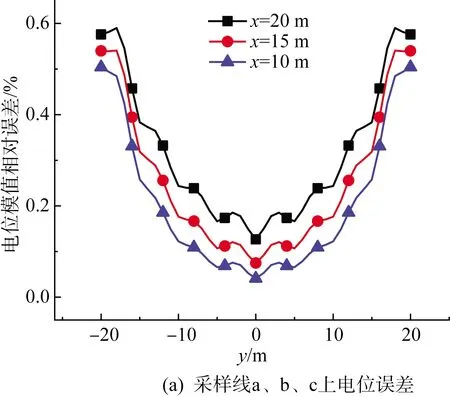
图9 两种计算方法采样线电位模值误差
计算结果显示,两种方法在计算杆塔周围10~20 m范围内电位时,电位模值误差不超过0.6%,且距离杆塔越近的采样线误差越小。两种方法计算不同输电线分段密度所需时间如表2所示,输电线分段越细计算效率提升越多,当输电线和杆塔总分段数为3 256时,效率提升可达40.95倍。

表2 计算时间对比
3 结论
针对输电线路在杆塔周围产生的电场计算问题,本文提出一种采用周期边界条件的简化计算方法。在模拟电荷法的基础上,利用周期条件解决输电线路三维模型中电荷在输电线两端聚集的问题,然后将距离输电杆塔较远,受杆塔影响可忽略的部分输电线电荷用无限长直输电线电荷代替,以减少待求未知数的个数,提高计算效率。
本文计算方法适用于计算考虑输电杆塔影响情况下,多档高压交流输电线路在非转角塔周围电场,且可考虑输电线路弧垂的影响。输电杆塔周围10~20 m范围内电位计算结果的误差可控制在0.6%以内,计算效率可提升数十倍,输电线模拟电荷建模分段越细,计算效率提升越明显。
