一个几何命题的向量证明及其初步应用与推广
2021-12-08张祯珞陈树康
张祯珞 陈树康
(罗源第一中学,福建 福州 350600)
一、命题呈现
命题:如图1,在平行四边形ABCD 中,若E、F 分别是AB、AD 边上除点A 外的点,且AD=mAF,AB=nAE,EF 交AC 于点G,则AC=(m+n)AG.
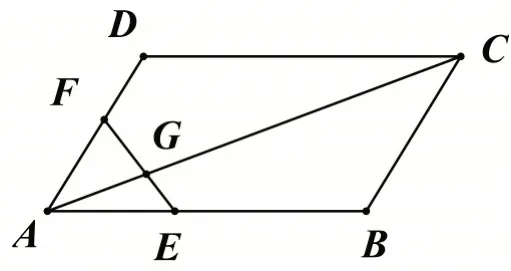
图1
向量是沟通代数与几何的桥梁,以向量为工具可以把几何性质的探究转化为向量的运算,在实际探究活动开展中,可以引导学生从向量解决平面几何问题的“三步曲”出发,尝试给出该命题的向量证明,增强综合运用数学知识的实践的能力.
二、命题的向量证明
证明:

三、命题的初步应用
在完成命题证明后可以尝试让学生思考命题的应用,可以从做过的习题等出发初步应用.
(一)在求线段比例问题方面的一些应用
例1.在ΔABC中,M 是BC 的中点,N 在AC 上且AN=2NC,AM 与BN 交于点P,求AP:PM 的值.
解:如图2,在AM 延长线上取点D 使AM=MD,显然四边形ABCD 为平行四边形.
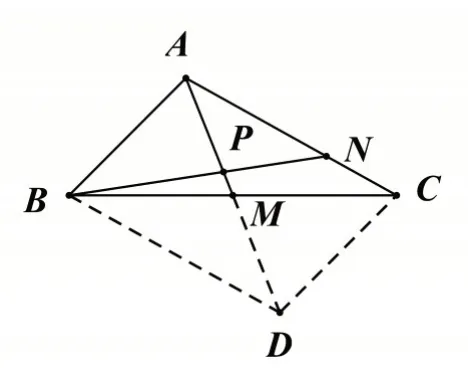
图2
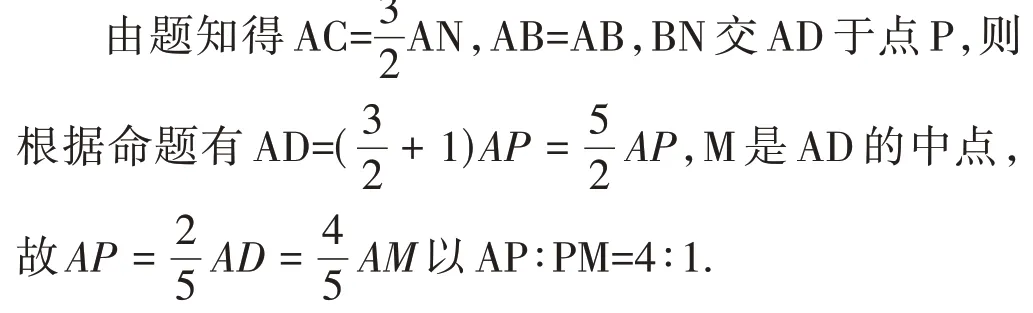
该题的解答利用了化归转化的数学思想,其实由该题可将命题进行特殊化,可得如下结论:
推论1:在△ABC中,M 是BC 的中点,若点N 在AC 上且AC=λAN(λ≠1),AM 与BN 交于点P,则有AP:PM=
证明类似于例1,这里从略.特别的当λ=2 时,由推论1 可得另一个常用的结论:
推论2:在△ABC中,重心G 到各顶点的距离与到相应顶点所对边的中点的距离的比都是2:1.再从课内熟悉的情形切换到课外的探索,可以引导学生思考若应用该命题来进行等分线段应该如何进行.
(二)在任意等分线段方面的应用[1]
从命题中,我们认识到,当m、n 为整数时就能得出任意等分线段的新方法,具体做法如下:如下图3,以被截线段AB 为对角线任意作一平行四边形,其对角线CD 将AB 二等分,过此二等分点E 作平行四边形的两邻边的平行线分别交两邻边于F、G,连结D、F 的线段与AB 的交点H 是AB 的一个三等分点,F、G 的连线与AB 的交点I 是AB 的一个四等分点;同样作出两邻边的三等分点J、K,四等分点N、P,可作出被截线段的五、六、七、八等分点L、M、O、Q……
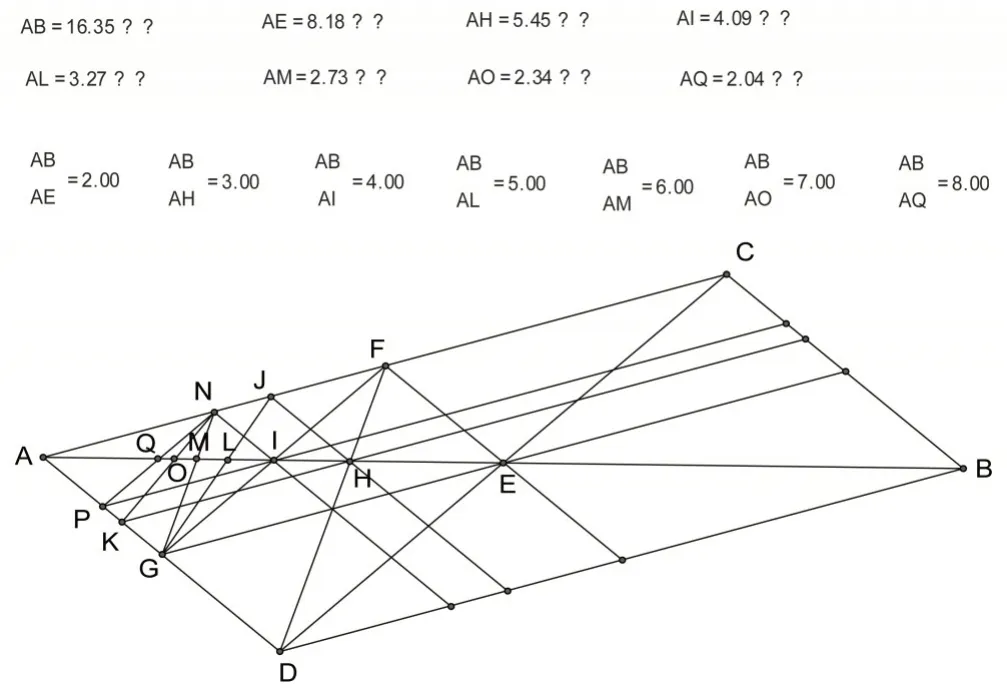
图3
这种作图法不用一等分、二等分……一步步作出所要的等分,比美国中学生发现的第二种众所周知的任意等分线段的作图法速度更快,更具一般性与实用性.
四、命题的推广
类比于平面上命题的结论,可得其在三维空间中的推广:
推广:在平行六面体ABCD-A'B'C'D'中,若E、F、G 分别是棱AD、AB、AA'上除点A 外的点,且AD=mAE,AB=nAF,AA'=kAG,面EFG 交AC'于点P,则AC'=(k+m+n)AP.
证明:如图4,连结AC 交EF 于H,▱ABCD中AD=mAE,AB=nAF,
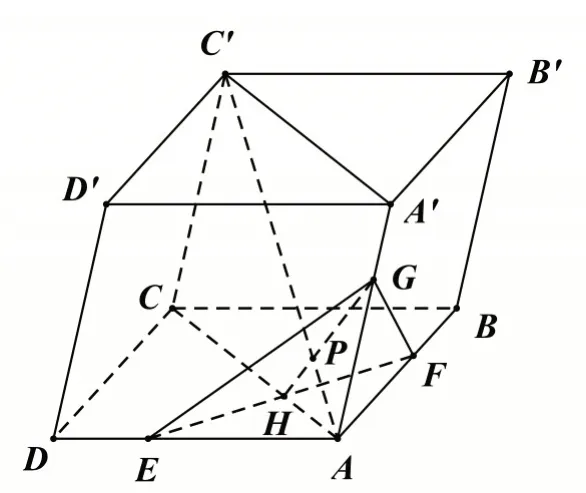
图4
根据命题有
AC=(m+n)AH——①
又AC、AC'、AA'共面,
则H、P、G 三点共线,
在▱ACC'A'中
AA'=kAG——②
由①②根据命题有
AC'=(k+m+n)AP.
特别地,当面A'BD∩AC'=P时,AC'=3AP,即体对角线AC'被截面A'BD三等分;另外推广本身也可以用空间向量来证明,留待师生在后继教学中进一步解决.
