一种管道探测蛇形机器人的建模仿真与实验研究

邓 蕊，王亚慧，邢利辉，侯坤昊

(北京建筑大学 电气与信息工程学院，北京 100044) E-mail：18833633026@163.com

1 引 言

管道运输凭借方便快捷、运输量大、成本低等优点，在燃气输配等领域有着至关重要的作用.然而大量的管道在投入运营后，长期受到运输介质、外部环境的腐蚀以及外力的冲击等影响，很可能出现管道裂纹、泄露、截留面积减小等.所以就需要定期对管道进行检查、维护和清洁保养[1].由于管道多是深埋地下且大多输送介质是对人体有害的，使得工作人员无法直接对管道进行检测和维修.

基于此，业内的研究人员提出了利用机器人替代人对管道进行日常维护和检测的新思路[2，3].经过近些年的研究发展，目前用于管道探测的机器人主要有轮式[4]和履带式机器人[5].但这两类机器人仅适应于大直径水平管道的检测，对于小直径以及垂直管道却无能为力了.针对此背景，我们提出并研制了一种用于管道内部检测的蛇形机器人，适用于200～500mm的管径.该蛇形机器人在管道中以行波或螺旋的多步态方式运动，能适应各种管道不同的管径要求，利用其在管道内灵活运动的特点进行管道检测，对可能出现的安全隐患进行排查.

2 蛇形机器人机械结构的设计

由于管道具有不同的管径和材料特性，且内部空间狭小、复杂，所以蛇形机器人需具备轻量、小型、灵活运动等特性[6].其样机采取关节模块化的设计，根据不同直径的管道灵活地增减模块数量来实现重组[7，8]；关节之间使用轻质铝合金部件进行连接，选用RDS3115大扭矩舵机来保证运动时有足够的动力；考虑蛇形机器人与管道间为软接触，设计了韧性较强、摩擦力较大的圆柱形橡胶外壳；为具有稳定的能源供给，采用拖缆的形式供电；为使机器人有效完成管道多步态运动和检测作业，采用正交连接的方式串联成蛇形机器人的样机.蛇形机器人要创建空间中的三维运动[9]，需要具备3个前提条件：1)每个模块的舵机必须提供足够的扭矩来维持其角度输出[10]，采用大扭矩的舵机来满足动力需求;2)关节间的铝制连接件必须具有足够的结构完整性，可保证其承受力和刚性强度足以抵制蛇形机器人运动时而产生的力;3)蛇形机器人依靠外壳与管道摩擦向前运动，于是外壳要有摩擦系数大、软接触和耐腐蚀特征，我们采用橡胶作为外壳材料.

2.1 模块的结构化设计

根据生物蛇的骨骼结构和运动机理，管道探测蛇形机器人可由多个重复模块来搭建[11].每个关节由一个舵机、两个不同尺寸的U型连接件、舵盘等部件组成.搭建蛇形机器人框架时，后一个关节在前一个关节的基础上，依次旋转90°连接.单个模块由舵机、U型承重件、控制器、外壳以及传感器等组成.舵机模块见图1.

图1 舵机模块的实物图Fig.1 Physical picture of steering gear module

蛇形机器人的动力源由每个模块中的双轴数字舵机提供，通过舵机的输出轴连接U型主支架提供运动时的扭力，利用舵机的另一端连接U型副支架使整个关节受力平衡.舵机由MCU的定时器输出的PWM波驱动，通过设定PWM波的不同脉冲宽度来控制舵机的旋转角度.利用内部的电位计闭环位置反馈电路，形成了能抵抗外部环境的强位置锁定功能.RDS3115舵机可在-90°-90°(摆臂和舵机平行默认0°)之间变化，其相应的参数见表1.

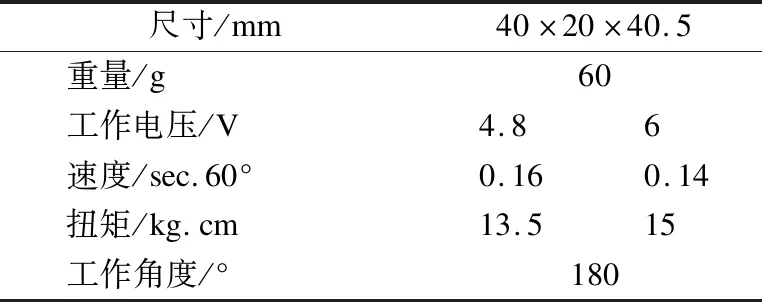
表1 舵机RDS3115的规格参数Table 1 Specifications of steering gear RDS3115

2.2 外壳设计

蛇形机器人的外壳设计是整个设计中关键一环，它不仅影响外壳与管壁的接触效果，还会影响蛇形机器人的运行速度.在运动的过程中，蛇的周身都可能与管道内壁进行接触，结合模块内部的舵机、控制器、U型连接件等部件的尺寸，将外壳设计成圆柱形外壳，并采用摩擦系数较高的(泊松比为0.324，杨氏模量为7.8×105psi)橡胶材质，这样就大大提高了蛇形机器人的运动效率和安全性.图2为外壳的整体样貌，目的是方便将舵机等部件装入壳中，进行装配.通过半个外壳两边的螺丝孔，加以固定.

图2 外壳的整体样貌Fig.2 Overall appearance of the shell

3 蛇形机器人建模与仿真

3.1 基于MATLAB的运动学建模与仿真

正交连接蛇形机器人是一种自由度较高、控制比较复杂的串联机器人.因在关节旋转角的最大容许范围内，关节的粗细不影响整个蛇形机器人的运动，所以这里将其抽象为空间连杆机构以简化模型的建立.而D-H分析法[12]是机器人运动学分析最常用的方法之一，利用坐标变换，能够把蛇形机器人的相对位姿准确地描述出来.

因蛇形机器人是移动机器人，无固定的底座，所以建立D-H坐标系时，基座标O0可任意，现以6关节为例.首先在每一个关节上建立一个局部坐标系，相邻关节之间采用4×4的变换矩阵来表述空间关系；然后依次通过矩阵相乘，求出每一个关节相对于基座标的位姿，直至末端.最后由此建立蛇形机器人的运动学方程.

其他关节的坐标系原点O位于旋转副轴线的中点，Z轴位于旋转副的轴线上，方向从被动摆臂指向主动摆臂，X轴方向指向下一个关节，位于蛇体的中心轴线上.另外，Y轴的方向由右手定则来决定.生成的D-H标准坐标系如图3所示，其它关节的坐标系之间存在3个约束关系(尾部基坐标系除外)：1)相连两个坐标系的Z轴相互垂直，逆时针依次旋转90°；2)下一个关节坐标系的原点在上一个坐标系X轴的输出轴线上；3)相隔两个坐标系的Z轴方向相反.我们假设坐标系O1和基座标的方向相同，根据图3建立的坐标系，生成蛇形机器人各关节之间的平移、旋转参数，其中θi为xi-1绕zi-1到xi轴的转角；di为xi-1沿着zi-1到xi轴的距离；Ai为zi-1沿着xi到zi轴的距离；δi为zi-1绕xi到zi轴的转角.具体如表2所示.

图3 蛇形机器人的D-H坐标系示意图 Fig.3 D-H coordinate system of snake-like robot

表2 蛇形机器人D-H参数表Table 2 D-H parameter table of snake robot

i=1，2，…，n

(1)

将表2中的具体参数代入式(1)，得：

(2)

根据上述的D-H参数表和转换矩阵的齐次变换，可求出蛇形机器人的运动学模型：

(3)

仿真验证：

利用MATLAB[13]，以32个关节为例，每个关节7cm，按照上述D-H分析法的建模思想，编写程序，根据相邻关节间的坐标变换矩阵，依次经过齐次变换求得末端关节相对于基座标的位姿，即建立起蛇形机器人的运动学模型.通过运动控制函数控制蛇形机器人运动学模型中的各关节运动，使各关节舵机转动相应的角度，获得蛇形机器人运动学正解；与系统机器人工具箱自带的正解函数比对，验证模型正确.图4为运动学正解的对比结果，即蛇形机器人尾部关节相对于基座标的总变换矩阵，4×4的齐次变换矩阵的最后一列为尾部关节相对于基座标的空间位姿(Px，Py，Pz).

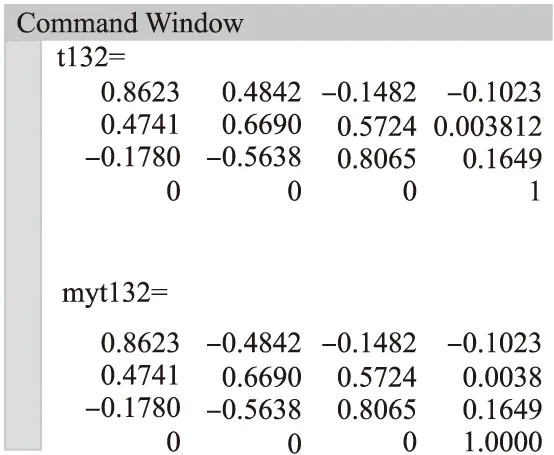
图4 运动学正解的结果比对Fig.4 Comparison of results of positive kinematics

通过多次更改运动控制函数中的参数，来获取大量不同直径管道中蛇形机器人螺旋运动的步态数据样本，通过粒子群算法得到控制参数与管道直径间的关系，可求出适应一定管径的优化运动控制参数.当管径300mm时(以300mm为例)，运动控制函数为θi=0.9sin(πt+1.6i)，i=1，2，3…n.将此运动函数应用到模型上，根据变换矩阵的齐次运算求出各关节相对于基座标的运动学正解，根据正解中的坐标信息绘出正交连接蛇形机器人在300mm管径内螺旋翻滚运动的空间位姿，如图5所示.

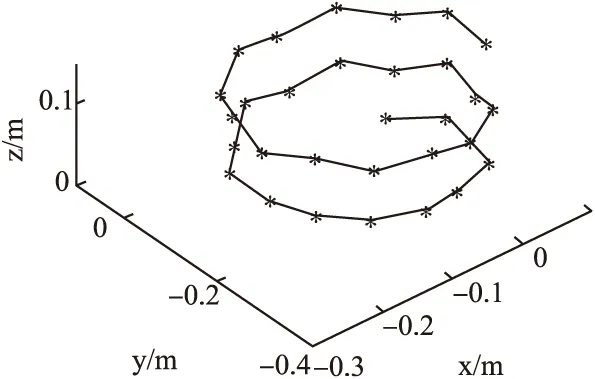
图5 300mm管径内t=1s时螺旋翻滚运动的空间位姿 Fig.5 Spatial position of spiral tumbling motion in 300mm pipe diameter with t=1s

3.2 基于ADAMS的动力学建模与步态仿真

机器人的动力学研究的是机器人力与运动之间的关系，其中最重要的是建立模型简化后多连杆机构的动力学方程.蛇形机器人的样机利用一连串的重复模块，采用正交的特殊方式连接.我们采用牛顿—欧拉的方法[14]，通过力与力矩间的平衡关系来建模.首先，建立全局坐标系下的运动平衡方程：

(4)

其中，i=1，2……n为蛇形机器人的n个关节；Fx，i、Fy，i、Fz，i是第i个关节分别在x、y、z轴上的摩擦力分力；Hx，i、Hy，i、Hz，i，Hx，i-1、Hy，i-1、Hz，i-1为第i个关节分别与第i+1个关节，第i-1个关节在x、y、z轴上的约束力.为了方便后续的计算，上述公式用矩阵表示为：

(5)

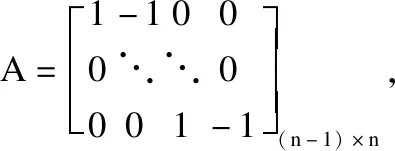
(6)

其中将各个角度的三角函数用向量和矩阵的形式来表示：cosφ=[cosφ1，cosφ2，…，cosφn]T⊂Rn，Cφ=diag(cosφ)⊂Rn×n，sinφ，sinμ，cosμ，Cμ，Sμ，Sφ同理.

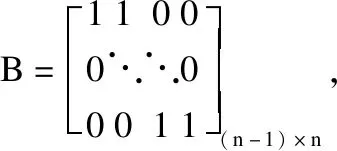
(7)

对X，Y，Z求两阶导数得：

(8)

在局部坐标系下，蛇形机器人第i个关节的受力分析见图6.

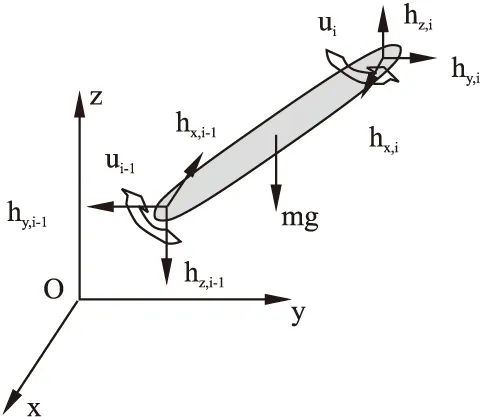
图6 三维空间连杆的受力分析Fig.6 Force analysis of three dimensional spatial connecting rod

其中ui，ui-1为第i个关节分别与第i+1，i-1个关节的舵机力矩.设逆时针方向为正，可得到下列的力矩平衡方程：

(9)

其矩阵形式为：

(10)

将hx，hy，hz代入式(10)中，令V=BT(AAT)-1B，P=BT(AAT)-1A，整理得动力学方程为：

(11)

仿真验证：

为了验证动力学模型的有效性，首先运用SolidWorks三维绘图软件建立蛇形机器人的实际模型，然后以Parasolid格式导入到ADAMS力学分析软件[15]，进行动力学的步态仿真.建模时，我们直接将蛇的框架和外壳装配在一起，进行绘图.以蛇形机器人在管道内的行波运动为例进行仿真分析，如图7所示.

图7 ADAMS中蛇形机器人管内行波运动Fig.7 Traveling wave motion of snake-shaped robot in ADAMS

1)根据蛇形机器人样机的实际尺寸，在SolidWorks中建立精确的几何模型以及管道、地面等实验环境；

2)根据D-H的标准分析法，在ADAMS中对蛇形机器人的14个模块建立相应的转动副和固定副约束，并给每个转动副添加运动约束函数.

3)按照实际设置每个模块和管道的质量、材质、刚度、透明度等参数，最大限度地还原实际情况，并在管道与每个模块间建立接触力约束，设置相关的摩擦系数等.

利用GSTIFF积分求解器对蛇形机器人的管内运动进行动力学仿真，当End Time=5s，Steps=800时，正交关节蛇形机器人可以在300mm管道中平稳地做行波运动，并可通过数据后处理来分析各关节速度、角速度、扭矩等情况，同时也为度、加速度的曲线,如图8所示.

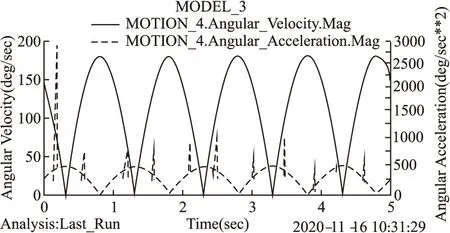
图8 关节4的速度、加速度曲线Fig.8 Velocity and acceleration curves of joint 4

4 蛇形机器人的运动实验

我们设计的蛇形机器人相邻关节间采取正交的结构，即一个偏移舵机接一个俯仰舵机，依次连接而成.样机共有14个单元模块，每个关节加装橡胶外壳后长65mm，宽56mm，重量为70g.利用蛇形机器人的样机搭建实验平台，测试其机械结构与控制策略是否合理、可靠，舵机运动函数是否有效.

用硬质、透明的有机玻璃管模拟实际管道展开室内运动实验(以行波方式为例)，通过控制函数计算各关节舵机的转角，并以此来控制舵机运动方式，即：

θi=Asin(wt+pi)+εi，i=2，4，6，…，n

(12)

式中，i表示舵机的序号；θi为第i个舵机的转动角度，A为舵机的最大容许转角，w为舵机运动的角频率，ρ为运动模式的控制参数，εi为角度补偿.

根据3.2小结动态仿真的运动控制函数，取A=1.6，w=π，ρ=0.3，εi=0时，蛇形机器人的样机可在300mm管径内平稳地实现行波运动，如图9(a)所示.根据实际刻度尺的测量，行波运动曲线的峰值为10.95cm，在10s内向前运动57cm，平均速度为5.7cm/s；另取A=1，w=π，ρ=0.3，εi=0时，蛇形机器人的运动如图9(b)所示，根据测量，行波运动曲线的峰值为7.3cm，在10s内向前运动53cm，平均速度为5.3cm/s；再取A=1.6，w=π，ρ=0.8，εi=0时，蛇形机器人的运动如图9(c)所示，根据测量，行波运动曲线的峰值为12.4cm，在6秒内向前运动了28cm，平均速度为4.7cm/s.

通过上述实验观察，蛇形机器人在运动中未出现侧滑，行波运动的波形由参数A和ρ共同来决定.对比图9(a)、图9(b)两组实验，在角频率w和ρ相同的情况下，A的值越大，蛇形机器人运动曲线的峰值越高，向前运动的速度相对越快.

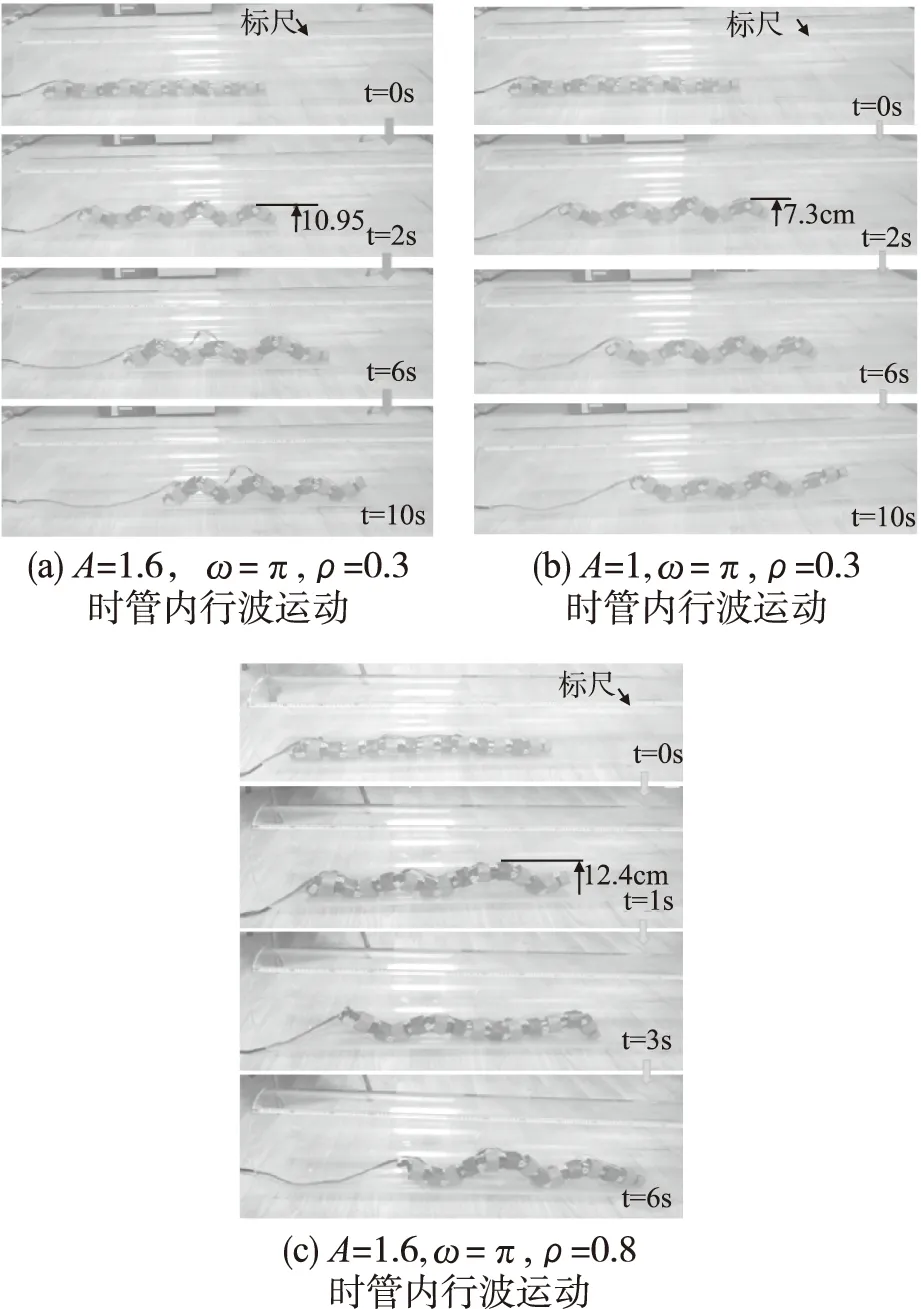
图9 管内行波运动(以300mm管径为例)Fig.9 Traveling wave motion inside the tube(take the pipe diameter of 300 mm as an example)

对比图9(a)、图9(c)两组实验，在角频率w和A一定的情况下，ρ的值越大，波峰数越少，峰值越高.为方便观察实验结果，采用了内部光滑的透明玻璃管道，现实中的管道存在一定的摩擦，蛇形机器人运动的速度会更快.通过大量的实验数据，在保证头部摄像机能获取清晰管内图像的前提下，以最快的运行速度来选取运动控制函数中的最优参数.

5 结 论

本文基于管道探测的特点，开发了一种灵活的多步态蛇形机器人，以期应用于200～500mm内径的传输气体的管道检测，补齐某些特殊场合下人工或其它非直接探测方法所不能解决问题的短板.具有较大的研究意义和实际的工程应用价值.本文通过研究生物蛇的骨骼结构和运动机理，结合应用环境，以及可重组的模块化思想构建了串联结构的蛇形机器人.获得了以下成果：

1)首先对蛇形机器人的机械结构和外壳进行了设计；

2)利用运动学和动力学仿真平台分别进行建模仿真，得出最优的控制参数，为现实的实验做参考意见；

3)最后通过样机实验来验证蛇形机器人管内运动的可行性、稳定性及运动能力.

纵观目前社会发展，机器人行业发展迅猛，仿生蛇形机器人有其独特的优点，在未来的管线探测、灾难救援、军事探险等方面有着特殊的应用价值和经济效益.