基于历史事故数据的液化天然气工厂设备风险事故预测研究
2021-12-07程松民
程松民
昆仑能源湖北黄冈液化天然气有限公司
我国液化天然气工厂的数量不断增加,一方面由于液化天然气工厂内设备的数量及类型相对较多,运行工艺相对较为复杂,在设备运行的过程中可能会出现各种类型的风险事故[1]。另一方面,液化天然气本身就属于一种易燃、易爆物质,如果设备运行出现风险事故,可能会引发更大的风险问题,由此可见,保障液化天然气工厂内设备的运行安全十分关键[2-4]。保障设备运行安全的前提是及时对风险事故进行预测,以便制定安全保障方案和风险预案。因此,对液化天然气工厂内的设备运行风险事故进行全面的预测研究十分重要。
目前,国内外学者对液化天然气工厂内设备运行安全问题进行了广泛的研究。田宇忠等[5]在综合考虑多米诺效应的基础上,对液化天然气工厂出现风险事故以后的后果进行了全面的研究,并对风险事故以后设备的损坏概率以及人员伤亡进行了全面的计算,研究结果表明,考虑多米诺效应前提下的风险定量评价结果更加的准确;王志寰等[6]对液化天然气工厂内设备泄漏风险问题进行了全面的研究,在研究的过程中,充分考虑了液化天然气工厂所处的地理位置,根据实际布置状况建立了三维预测模型,对泄漏风险问题进行了全面的预测,研究结果表明,所建立的三维预测模型相对较为准确,可用于液化天然气工厂泄漏风险预测及分析;HAMEED 等[7]建立了一种基于风险双目标的模型,对液化天然气工厂内的脱硫装置运行风险问题进行了全面研究,该模型可以为制定脱硫装置的维修决策提供指导建议。
通过对国内外研究现状进行分析可以发现,目前国内外的研究主要集中在单一设备的运行风险或者风险事故的危害评价方面,对于整个液化天然气工厂内设备风险事故的预测研究相对较少。为此,本次研究主要是引入了差分自回归移动平均(ARIMA)、最小二乘支持向量机(LS-SVM)以及BP神经网络(BPNN)三种类型的算法,提出了三种算法的组合方式,利用组合模型对液化天然气工厂内设备的运行风险事故进行了预测研究,可以为了解液化天然气工厂内设备风险事故的变化趋势以及制定安全保障措施提供指导建议。
1 风险事故预测难点分析
对液化天然气工厂内的设备风险事故进行预测的难度相对较大,其主要的原因有两点。首先,液化天然气工厂内的设备数量以及类型相对较多,液化天然气工厂主要进行原料气的净化、压缩、天然气的液化、储存等工作,其主要的设备装置包括净化装置、分离器、分馏塔、压缩机、换热器等[8-9]。在开展日常工作的过程中,各种类型的设备装置都可能会出现风险问题,且每种类型设备装置出现的风险事故问题各不相同,引起事故问题的原因也存在众多的差别,所引发的后果也存在较大的差距,这使得对风险事故进行预测的难度相对较大[10-11];其次,液化天然气工厂内的生产工艺相对较为复杂,各种类型的设备串联在一起,如果一种类型的设备出现风险问题,很可能会引发其他设备的风险问题,因此对液化天然气工厂内的设备风险事故进行整体性预测的难度相对较大。
针对液化天然气工厂内设备风险事故预测难度相对较大的问题,本次研究首先将设备的风险事故分为两种类型,分别是严重事故和一般事故(严重事故是指会造成人员伤亡和巨大经济损失的风险事故,一般事故是指会影响生产作业效率和经济损失较小的风险事故),所有设备的风险事故都将归结到这两种类型的事故中,然后对液化天然气工厂内的设备风险事故进行统一的预测研究。
2 数据来源及研究方法
2.1 某企业风险事故数据
本次研究所使用的数据来源于我国某液化天然气企业,该企业于2020 年发布了2008—2019 年的运营数据,运营数据中包含了设备运行风险事故类型、出现的原因以及所造成的危害。首先对所有的设备运行风险事故进行了统一的分类,将其分为严重风险事故和一般风险事故两种类型,对这两种类型的风险事故进行预测研究。该液化天然气工厂每季度都会针对不同的设备进行维护及检测,其2008—2019 年的风险事故情况见表1,2008—2019年设备维修情况见表2。

表1 2008—2019年某液化天然气企业设备风险事故情况Tab.1 Equipment risk accidents of a LNG enterprise from 2008 to 2019
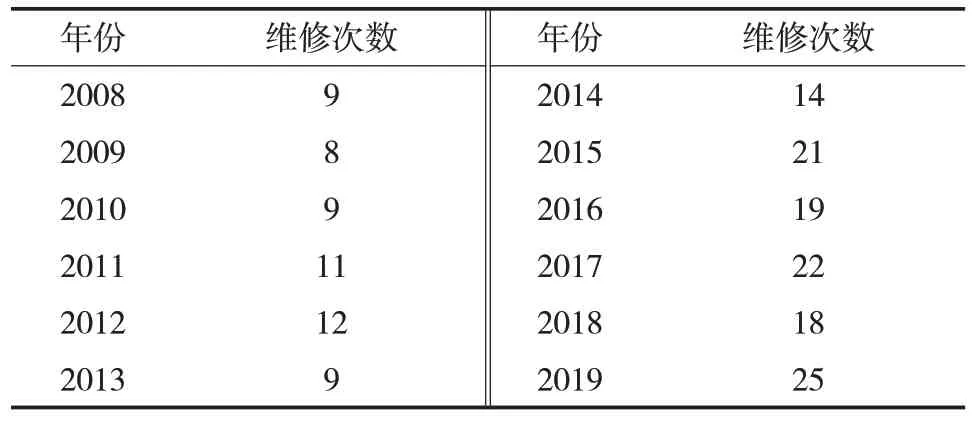
表2 2008—2019年某液化天然气企业设备维修情况Tab.2 Equipment maintenance times of a LNG enterprise from 2008 to 2019
2.2 模型理论基础
2.2.1 ARIMA模型
ARIMA 模型主要是通过将时间序列转化为随机序列进而对预测值进行全面的预测,该种类型算法模型的精度相对较高[12]。如果某一项数据具有季节性以及趋势性的基本特征,则可以使用该种模型将其表示为ARIMA(p,d,q)(P,D,Q)s季节模型,在该模型中共含有7项参数,其中p、q为自相关或者偏自相关的函数的阶数,d为该模型的差分次数,P、Q、D为季节性中的自相关、偏自相关函数的阶数以及函数的差分次数,s为周期[13]。这种模型可以表示为

式中:ε为随机误差;Φ(L)∇dY为在同一个周期之内不同周期点位置处的相关性;U(LS)∇Ds为在不同的周期之内相同周期点位置处的相关性。
在进行建模的过程中,首先需要对数据进行差分处理,然后对其进行周期性的观察,确定d的数值。例如在进行n阶的差分处理以后,其周期性已经消失了,此时就可以得到d=n;同时,通过差分的方式也可以确定D的数值。p和q的取值主要可以通过进行差分处理以后的ACF图以及PACF图进行确定,P和Q的数值一般都属于低阶情况,因此可以使用从低阶向高阶尝试的方法进行确定,在进行确定的过程中可以使用Ljung-Box 的方法进行检验,从而确定出最佳的模型。
2.2.2 LS-SVM模型
LS-SVM模型主要是在对SVM模型进行全面优化的基础上提出的一种算法模型[14]。该种模型可以通过对线性方程组进行全面求解的方式,进而对问题进行一定的简化,通过该种方式可以使得模型的计算效率得到提升[15-16]。同时,在构建模型的过程中需要一定量的数据,将数据转化到高维的空间之中进行回归处理,引入核函数避免出现维度灾难问题。非线性的支持向量机可以通过以下方式进行求解

式中:W为拟合函数;yi为第i个输出向量;xi为第i个输入向量;i、j为向量序号;ε为残差;n为输出向量的数量;l为输入向量的数量。
上述方程的约束条件为

式中:C为正则化参数。
在得到拉格朗日系数αi、以后,该函数f(x)可以表示为

式中:SVs为训练样本的空间;K(xi,x)为核函数。
2.2.3 BP神经网络模型
BP 神经网络算法属于一种常见的预测类算法,在使用该种算法的过程中,工作将会正向传递,误差将会反向传递[17-18]。在BP神经网络算法之中,每个样本数据都会有m个输入,同时还会有n个输出,在输入层I与输出层O之间还含有隐含层H,其主要是验证相对误差平方和最小的方向,对阈值进行反复的修正,进而使得模型的预测误差达到最低[19]。其误差函数可以表示为
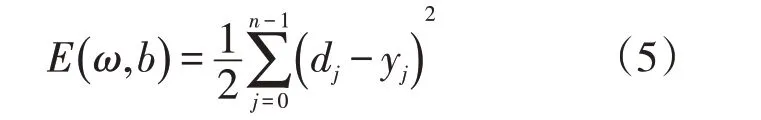
式中:E为误差函数;ω为权重;b为阈值;n为输出数据的数量;j为某项数据;dj为模型的输出结果;yj为数据的真实数值。
2.3 组合模型构建步骤
组合模型的构建分为以下步骤:
(1)首先建立ARIMA 模型,并将液化天然气企业相关指标数据输入其中,然后对统计量和显著性进行一定的拟合,最终得到最佳的模型Y1=f(x)。
(2)然后建立LS-SVM模型,通过使用交叉验证的方式得到模型的参数,即Y2=s(x)。
(3)使用相关数据对BP 神经网络模型进行全面的训练,最终得到模型的参数,即Y3=n(x)。
(4)根据DS 证据理论,对各个模型的权重ai进行确定,最终得到用于液化天然气工厂设备风险事故预测的模型Y=a1Y1+a2Y2+a3Y3[20-21]。
2.4 自变量筛选
对于液化天然气工厂设备运行安全而言,其影响因素相对较多,包括设备的运行时间、利用率以及工作人员技术水平等,在对液化天然气企业进行设备风险预测的过程中,虽然需要建立时间序列模型,但是也必须考虑这些影响因素对模型脆弱性的影响,设备运行风险的脆弱性主要来源于工作人员以及外界环境,本次研究所考虑的设备风险影响因素主要有7 项:①设备运行时间x1;②设备年限x2;③设备利用率x3;④工作人员工作年限x4;⑤工作人员数量x5;⑥恶劣天气(雷雨、大风出现的天数)状况x6;⑦经济效益x7。
3 应用实例分析
3.1 数据预处理
本次研究主要以我国某大型液化天然气工厂为例,其运行时间已经超过10 年,该工厂内设备风险事故的时序图如图1所示。通过对时序图进行分析可以发现,设备出现风险事故的次数具有较大的波动,且随着时间的变化,风险事故的次数逐渐升高。其中2008—2012 年该工厂设备出现风险事故的次数相对较少,2013 年以后出现设备风险事故的次数呈现出波动式增加。在进行建模的过程中,将该工厂2008-2017 年的数据作为模型的训练样本,对2018 年、2019 年的数据进行预测。为了对季节性因素进行分解,提高数据的稳定性,对数据进行分解,分解结果如图2所示。通过对分解以后的季节性时序图进行分析可以发现,该工厂内设备风险事故也呈现出了明显的季节性特征,由此可确定s=12。
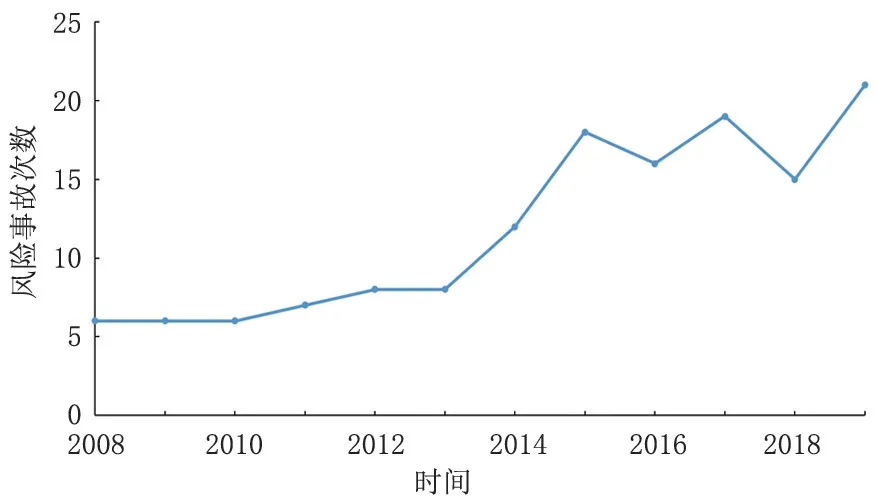
图1 2008-2019年某液化天然气工厂设备风险事故时序图Fig.1 Sequence diagram of equipment risk accidents in a LNG plant from 2008 to 2019

图2 2008-2019年某液化天然气工厂设备风险季节性时序图(01表示第一季度,03表示第三季度)Fig.2 Seasonal sequence diagram of equipment risk in a LNG plant from 2008 to 2019(01 represents the first quarter,03 represents the third quarter)
3.2 ARIMA模型识别
残差的自相关函数图以及残差的偏自相关函数图如图3 和图4 所示。通过对两图进行分析可以发现,当残差的滞后值达到lag=14 时,两种函数出现了截尾性现象,同时其自相关系数不等于0,可以将参数q和Q均设定为1;当残差的偏自相关函数滞后值lag=14 时,其偏自相关系数也不等于0,所以可以将参数p和P均设定为1。

图3 残差的自相关函数图Fig.3 Autocorrelation function graph of residuals

图4 残差的偏自相关函数图Fig.4 Partial autocorrelation function graph of residuals
将Y1作为模型中的因变量,将表2中的影响因素作为自变量,使用matlab软件对各个阶数进行全面的计算,最终得到最佳的模型是ARIMA(1,1,1)(1,1,1)14,该模型的各种统计量见表3。

表3 最佳模型的统计量Tab.3 Statistics of the best model
通过对表3进行深入分析可以发现,残差的自相关函数以及偏相关函数都处于可信的区间之内。其中Ljung-Box的统计量数值达到了22.84,其显著性也达到了0.082,证明这种差异并没有统计学上的意义,可以将原假设否定,即残差序列存在白噪声,序列属于一种随机的序列,平稳后的R2(表示相关系数)达到了0.721,正态化的BIC 值也达到了-2.37,说明模型的拟合度相对较好,可以用于数据的预测。该最佳模型的t检验结果见表4。通过对表4进行分析发现,该最佳模型已经通过了t检验。

表4 最佳模型的t 检验结果Tab.4 t test results of the best model
3.3 LS-SVM模型识别
在使用LS-SVM模型算法的过程中,其预测的精度与核函数以及相关参数设置有关,本次研究使用的核函数为径向基核函数,公式为
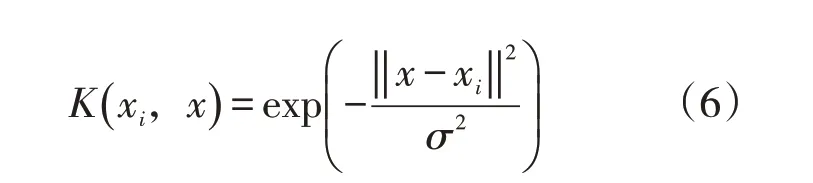
在使用径向基核函数的前提下,可以通过多次试算的方式,确定两种参数数值,即C=12,σ=0.001,通过设定参数使得模型的泛化能力得到了增强。为了防止出现计算饱和问题,需要对偏差进行归一化处理,进而对2018 年和2019 年的数据进行全面的预测。
3.4 BP神经网络模型识别
在使用BP 神经网络模型的过程中,输入层为年度、季度以及表2 中的7 项影响因素,在考虑样本数量的前提下,将隐含层设定为1,输出层为该液化天然气工厂设备风险事故的次数,激活函数使用默认函数,错误函数选择平方和方式,训练样本的个数为40个,测试样本的个数为8个,该模型的统计量见表5。

表5 模型统计量信息Tab.5 Model statistics information
3.5 组合模型预测
ARIMA 模 型、LS-SVM 模 型以及BP 神经网络模型等三种模型的预测结果与实际值之间的对比情况见表6。根据相对误差的大小,进而可以确定各种模型的权重,权重确定情况见表7。

表6 三种模型预测结果Tab.6 Prediction results of the three models
通过对表7进行分析可以确定,本次研究提出的组合模型是:Y=0.241 584×Y1+0.311 784×Y2+0.446 632×Y3。使用组合模型对2008—2017 年该液化天然气工厂设备风险事故进行拟合,拟合结果如图5所示。

表7 权重分配情况Tab.7 Weight distribution
通过对图5进行分析可以发现,组合模型的拟合结果与实际风险事故的发展趋势相同,每个季度的风险事故拟合值都处于置信区间之内。组合模型的最大相对误差为16.00%,出现在2014 年的第二季度,2008 年第二季度、2011 年第二季度以及2012 年第二季度的相对误差也相对较大。最小相对误差小于1%,拟合值在拐点位置处的误差相对较大。由此可见,该组合模型可以反应出该液化天然气工厂设备风险事故的波动情况,拟合值与实际状况之间具有很强的重合度,证明组合模型的精度相对较高。
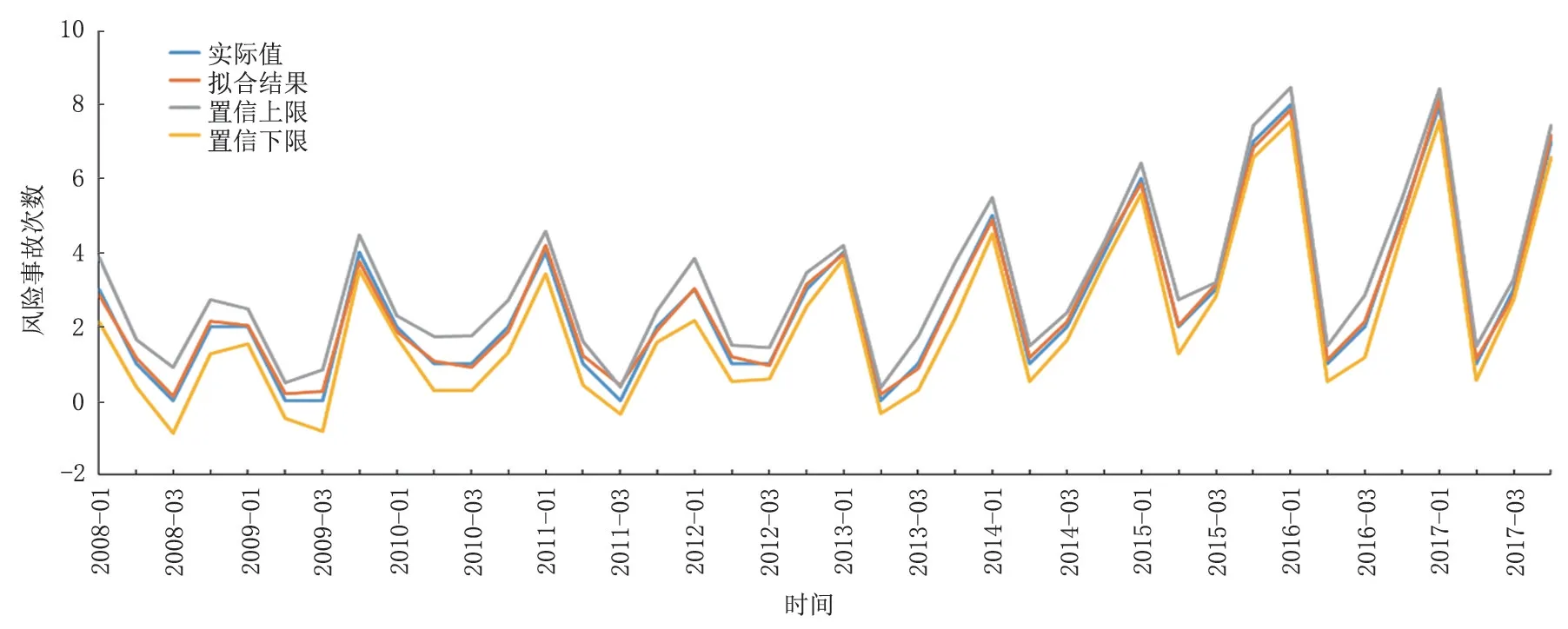
图5 2008—2017年某液化天然气工厂设备风险事故次数拟合结果Fig.5 Fitting results of the number of equipment risk accidents in a LNG plant from 2008 to 2017
3.6 预测结果分析
使用组合模型对该液化天然气工厂2018 年和2019 年的设备风险事故进行预测,并与实际状况进行比较,预测结果如图6 所示。通过对图6 进行分析可以发现,该液化天然气工厂内的设备风险事故次数处于波动式上升阶段,随着时间的推移,出现风险事故的次数逐渐增加。组合模型的预测结果与实际状况相吻合,与单一的模型相比,组合模型的精度得到了较大的提升。通过对预测结果进行全面的分析可以发现,组合模型可以反应出该液化天然气工厂设备风险事故次数的动态变化情况,可以对液化天然气工厂设备风险事故进行短期的预测。组合模型的精度虽然得到了提升,但是仍然存在一定的误差,模型的精度仍然有待提升。通过研究可以证明,使用该组合模型可以对液化天然气工厂内所有动设备以及静设备出现风险事故的次数进行全面的预测,而出现风险事故并不意味着设备失效,但必然会对其运行效率以及运行安全产生影响。因此,液化天然气工厂内的工作人员需要根据风险事故的发展趋势,提前制定有效的预案,及时解决设备的运行问题,保障生产效率和生产安全。

图6 2018—2019年某液化天然气工厂设备风险事故预测结果Fig.6 Prediction results of the equipment risk accidents in a LNG plant from 2018 to 2019
4 结论
在本次研究中,以某液化天然气工厂2008—2019 年的设备风险事故真实数据为依据,进而建立了设备风险事故预测的组合模型,进行了模型的实例验证。通过本次研究主要可以得出以下结论:
(1)本次研究提出的组合模型主要是根据设备风险事故历史数据的线性以及非线性特征,对特征进行提取,然后进行参数估计以及验证,验证结果显示,其预测结果可以为液化天然气工厂企业制定设备风险事故的预防措施提供数据支撑。
(2)在使用组合模型的过程中,充分考虑了其他因素对设备风险事故次数的影响,对单一模型的误差进行了全面的修正,结果显示,通过使用大数据对样本进行全面的训练,可以使得组合模型的精度得到明显的提升。使用组合模型可以对液化天然气工厂内设备风险事故出现次数的发展趋势进行预测,预测精度相对较高。但是由于液化天然气工厂内设备风险问题较为复杂,所以在预测的过程中只能进行季度性预测。
(3)本次研究主要是通过使用历史数据对未来状况进行预测,但是在同一个时间点可能会出现多种类型的设备风险事故,此时就会出现离群现象,进而使得模型的预测精度降低,因此模型在使用的过程中,液化天然气企业需要从实际情况出发,将预测周期控制在2~3年,这可以与液化天然气工厂企业制定年度计划相吻合,更利于液化天然气企业制定完善的预防措施,全面防止出现设备风险问题。
