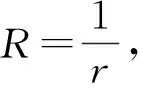带脉冲的一阶奇异微分方程周期解的存在性

何志乾

(青海大学基础部，青海 西宁 810016)

现代科学技术的许多领域中,都涉及到脉冲微分方程，而作为描述瞬动型系统的一种数学模型——脉冲微分方程的研究开始于上世纪60年代Mil′man和 Myshikis的工作。脉冲微分方程在概率论与数理统计学科中有重要应用背景，是研究状态发生突变的动力学行为的基本工具，其定性理论的研究推动了许多应用学科的发展，例如，控制理论[1-3]、种群动力学[4]、药物的化疗治疗[5]以及一些物理问题[5-6]。同时，从数学的角度来看，脉冲微分方程解的定性性质也受到许多学者的关注[8-14]。一些经典的工具被用来研究这类问题，例如，上、下解方法[9-10]、不动点理论[11-14]；另一方面，一些学者研究了没有脉冲效应的周期问题[13-15]；但关于研究含脉冲项的周期边值问题在数学上更有实际意义。本文将研究一类更广泛的带脉冲的一阶奇异微分方程正解的存在性，值得注意的是，本文的主要结果是文献[13-16]的本质推广，并可为脉冲微分方程的研究提供理论依据。

1 预备知识

受以上文献的启发，本文研究一类一阶脉冲微分方程

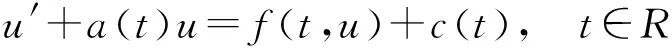
(1)

(2)

其中脉冲Ik:R→R,k=1,…,p是连续函数。PC(N)表示u:N→R使得u(t)在t≠tk处连续，在t=tk处左连续,右极限u(tk+)存在，k=1,…p。特别地，PC(N)为装备了范数‖u‖PC=supt∈∞|u(t)| 的Banach 空间。 对给定的函数ζ∈L∞(0,T)，记ζ*,ζ*分别表示ζ的本质上确界和本质下确界。

为方便起见，记

σ:=max{μ,α}，δ:=max{ν,β}

令A(T)>0，则线性边值问题

(3)

当且仅当h不恒为零时有唯一解

其中

易知若A(T)>0，则G(t,s)>0。令

定义算子T:PC(N)→PC(N)

引理1T是全连续算子，此外，x为(1)和(2)的周期解当且仅当x是T的不动点。

证明运用类似于文献[17]中引理 2.1 的方法，易证该引理，故略去不证。

2 主要结果

(H1) 存在b,e∈L1(0,T)满足b,e>0,α,β∈(0,∞),m≤1≤M，使得

且

则边值问题(1)和(2)至少存在一个正T周期解。

证明令CT是T周期连续函数集合，由引理1和Schauder不动点定理可知，如果T映闭凸集

K={u∈CT:r≤u(t)≤R, 对任意的t∈[0,T]}

到它自身，其中R>r>0,则定理得证。

对任意给定的u∈K，令

I1:={t∈[0,T]|r≤u(t)

I2:={t∈[0,T]|R≥u(t)≥M}

I3:=[0,T](I1∩I2)

给定u∈K，由Green函数G以及f的非负性，有

γ(t)≥γ*=:r

令

则由(H1)可知Λ2<∞，则对任意的u∈K,

定理2令A(T)>0且γ*=0，并假设如下假设条件成立

(H2) 存在b1,b2,e∈L1(0,T) 满足b1,b2,e>0,α,β,μ,ν∈(0,1)使得

并且

且

则边值问题(1)和(2)至少存在一个正T周期解。

证明运用同样的方法和记号，定义如下闭凸集

K={u∈CT:r≤u(t)≤R对任意的t∈[0,T],R>1}

运用Schauder不动点定理，如果T映闭凸集K到它自身，则证明可证。这里R,r是正常数并且满足R>r>0且R>1。

对给定的u∈K，令

J1:={t∈[0,T]|r≤u(t)<1}

J2:={t∈[0,T]|R≥u(t)≥1}

则对任意给定的u∈K,由G和f的非负性可得

另一方面，对任意的u∈K，

因此，Tu∈K，如果选择r,R使得

因为σ,η<1和ν<1，故这些不等式成立当且仅当R足够大。

注值得注意的是定理2对c(t)≡0也成立，这种情况也是γ*=0的特殊情形。

定理3令A(T)>0且假设(H2)成立，令

如果γ*≤0并且

则边值问题(1)和(2)至少存在一个正T周期解。

证明运用类似的方法，不难验证定理3也成立，我们省略其证明过程。

自然界任何事物的运动规律都是复杂的，常常是确定性和随机性的过程相互交织在一起,任何时刻都可能由于外界随机因素的干扰而使系统状态发生突变。即实际脉冲发生的时刻往往不是确定性的,也就是说实际的脉冲时刻应该是一列随机变量。于是，对实际过程的分析也就有必要从确定性观点转到随机性观点。本文研究了一类特殊的，在概率论与数理统计学科中有重要应用背景的一类数学模型——带脉冲的一阶奇异周期边值问题。本文分三种情况探讨了该边值问题正周期解的存在性，所得结果不仅为这类问题的研究提供了重要的理论指导，在工程中也有重要的应用价值。