基于神经网络分位数回归的人民币汇率概率密度预测

李艳萍，赵 冬，陈士俊

（1.安徽农业大学经济技术学院，安徽合肥 230036；2.淮北职业技术学院 基础部，安徽淮北 235000；3.招商银行合肥分行，安徽合肥 230031）

1 引言

2005 年7 月，中国人民银行宣布汇率制度改革，正式实施以市场供求为基础的有管理浮动汇率制度。2010 年6 月，中国人民银行宣布进一步推进人民币汇率改革。人民币兑美元汇率单日浮动幅度不断增加，分别由2012 年4 月的0.5%扩大至1%，由2014 年3 月的1%扩大至2%。2015年8 月，中国人民银行决定调整人民币对美元汇率报价机制，做市商可以参考前日外汇市场收盘汇率信息来提供中间报价，能够更加真实地体现外汇市场中的供求关系。自人民币实行汇率制度改革以来，人民币兑美元汇率总体呈现升值趋势，从2005 年7 月的1 美元兑8.24 元人民币升值到2014 年12 月的1 美元兑6.12 元人民币。近年来，人民币兑美元汇率呈现出剧烈波动态势，截止2017 年2 月26 日1 美元兑6.67 元人民币。

随着中国金融市场不断开放与经济全球化进程不断加深，人民币汇率在整个国民经济中的地位和作用越来越重要，特别地直接影响到贸易结算与国际收支等方面。在便于经济下行背景下，能够准确预测人民币汇率变化趋势，对于人民币国际化与个人投资、企业决策等都具有重要指导意义。

迄今，国内外大量文献研究人民币汇率预测问题，大体可以划分为三类。第一类，基于购买力平价（perchasing power parity,PPP）理论的研究。郑兰祥[1]研究认为，PPP 在长期内可能存在均值回归现象，但短期内不会明显出现。刘柏等[2]研究表明，中国由于加入世界卫生组织（WTO）时间不长，并不满足自由贸易前提假设中的“一价定律”，导致在PPP 难以准确预测人民币汇率。毕玉江等[3]实证检验了PPP 预测汇率的效果，回归分析结果表明：PPP 预测的汇率严重偏离实际汇率。第二类，基于汇率影响因素的研究。贺昌政等[4]从工业增加值、进出口总额、通货膨胀率、外汇储备、实际利差、广义货币M2 等方面，细致研究了人民币汇率影响因素，进而运用数据挖掘等模型与方法，对人民币兑美元汇率进行了预测。第三类，基于时间序列分析的研究。刘柏等[2]认为，可以从时间序列的角度研究汇率变动规律，自回归移动平均（autoregressive moving average,ARMA）模型也许是最佳选择。许少强等[5]考虑了人民币汇改的“一篮子货币”，参考美元汇率加权计算方法，运用ARMA 模型，较好地预测了人民币汇率的中长期趋势。郭琨等[6]主要使用了较为新颖的周期-ARMA 模型，成功预测了人民币兑美元汇率的短期波动。

然而，人民币汇率存在非线性形成机制，线性ARMA 模型往往难以取得理想的预测效果。因此，一些非线性模型与方法纷纷被引入汇率预测，取得了较好的实证效果。Santos 等[7]采用神经网络（NN）等非线性模型，预测了巴西雷亚尔兑美元汇率，发现其样本外预测精度高于自回归移动平均-广义自回归条件异方差（autoregressive moving average-generalized autoregressive conditional heteroscedasticity,ARMA-GARCH）模型。刘柏等[2]运用了平滑转移自回归（smooth transition autoregression,STAR）模型，研究了人民币汇率预测问题，认为人民币汇率具有明显的非对称性与非线性特征。孙柏等(2009)[8]、王轩等[9]建立了多层感知机（multi-layer perceptron,MLP）神经网络模型，分别预测了人民币兑港币、美元、日元、欧元等的汇率。熊志斌[10]将ARIMA 模型与NN 模型相结合，建立了人民币汇率预测模型，发现其能够有效地预测人民币兑美元、日元、欧元等的汇率。王晓辉等11]融合独立成分分析（independent component analysis,ICA）方法与反向传播神经网络（back propagation neural network,BP-NN）模型，提出了ICA-BP 神经网络并将其应用于预测人民币兑美元、日元、欧元、英镑等的汇率，取得了较好的预测效果。

综合上述，人民币汇率预测中大多采用点预测方法，只能关注响应变量平均取值变动规律。从统计学角度而言，这些方法实质为均值回归。当人民币汇率散布较大或者呈现非对称分布时，均值回归往往缺乏代表性，需要使用分位数回归（quantile regression,QR）方法进行概率密度预测，详见张蕾等[12]、苏静文等[13]与许启发等[14]的研究工作。Taylor[15]提出的神经网络分位数回归（quantile regression neural network,QRNN）模型为人民币汇率预测提供了便利，该模型具有强大的功能，一方面通过NN 模型拟合非线性，另一方面通过QR 模型揭示解释变量对响应变量整个条件分布的异质影响。更进一步，Xu 等[16]与许启发等[17]使用QRNN 模型提出了概率密度预测方法，并将其分别应用于资产收益与风险方面的预测研究。

为此，本文运用QRNN 模型，研究人民币汇率的条件概率密度预测问题。在QRNN 模型建立中，主要通过NN 模型模拟人民币汇率的非线性形成机制，通过QR 模型揭示人民币汇率整个条件分布的异质性与变动规律。选取人民币兑美元汇率作为研究对象，开展条件概率密度预测研究，一方面通过QRNN 模型提高人民币汇率预测精度，另一方面通过QRNN 模型预测人民币汇率完整条件分布，为科学决策提供依据。

2 人民币汇率影响因素分析

为准确预测人民币汇率（（exchange rate,ER）变化规律，需要全面系统考虑各因素的影响，从而建立相应的QRNN 模型。

（1）贸易收支

在国际贸易中，当出口总额（EX）小于进口总额（IM）时，贸易收支通常出现逆差，从而增加对外债务，往往引起外币需求增加、本币需求减少，最终导致本币贬值；反之，则反是。因此，贸易收支与本币汇率通常表现出正向的相关关系。左相国等[18]研究表明，中国持续的贸易收支顺差，是人民币汇率走高的重要支撑。郭莹莹[19]的实证结果表明，中国出口规模大幅增加，引起了人民币汇率的升水。刘艺欣等[20]与苏静文等[13]研究表明，我国贸易收支与人民币汇率之间呈现明显的联系性特征。

（2）外汇储备

在贸易收支顺差时，外汇供给往往大于外汇需求，促进本币升水。此时，货币当局特别关注外汇储备（（foreign exchange reservrs,FER），以此来维持本币汇率稳定。实际中，FER 是一种维持本币汇率稳定的常用工具。高铁梅等(2013)[21]研究表明，中国国际收支经常账户、资本与金融账户的“双顺差”不断扩大，中国人民银行不断吸纳“双顺差”所产生的外汇并形成FER，据此平抑人民币过快升水。陈建勋等(2014)[22]开展了类似研究，认为FER 是影响汇率的关键因素，在稳定本币汇率与实现国际收支平衡等方面贡献了积极作用。

（3）通货膨胀

在通货膨胀严重时期，本币贬值并且实际购买力下降。这样，通货膨胀与本币汇率往往呈现负向的相关关系。高铁梅等[21]研究表明，人民币的升值预期往往引致热钱大量涌入、FER 增加，人民币需求剧增与人民币大量投放，带来人民币对内贬值，推动国内物价水平攀升。郭莹莹[19]与杨小军[23]考察了作为通货膨胀的居民消费价格指数（（consumer price index,CPI），发现CPI 能够显著影响到人民币汇率。

（4）货币供应量

毫无疑问，货币供应量是人民币汇率的重要影响因素，它与本币汇率呈现负向的相关关系。一般地，随着货币供应量增加，本币出现供过于求，导致本币贬值。相反，货币供应量减少，本币就会出现供不应求，导致本币升值。郭莹莹[19]对中国进行了实证研究，定量分析了取广义货币供应量（M2）与人民币汇率之间关系，结果显示：随着M2 逐年增加，人民币对内贬值，其国内市场购买力不断下降。

（5）利率水平

利率也是人民币汇率的重要影响因素。利率平价理论告诉我们，如果两国实际利率差异显著高于两国即期与远期汇率差异，资本从低利率国家流出，最终流向高利率国家，最终导致外汇供给大于外汇需求，从而促进本币升值。金中夏等[24]研究表明，在中国由于利率市场化程度并不高，资本流动受到一定程度的管制，基于利率平价理论的汇率预测往往难以奏效。郭莹莹[19]研究指出，以伦敦银行间同业拆借利率（（London Inter Bank Offered Rate,LIBOR）为代表的国际市场利率显著影响了中国汇率变化。具体地，当LIBOR 下降时，资本流入会带来人民币升值；反之，则反是。

（6）外商直接投资

一般地，外商直接投资（foreign direct investment,FDI）与汇率呈现正向的相关关系。外商直接投资增加不仅带来资本持续流入，而且促进对外贸易增长，有利于实现贸易顺差，最终引起本币升值。中国自2001 年加入WTO 以来，不断放宽外商投资的条件限制，有效促进了外商直接投资增长。赵迎新[25]与彭红枫等[26]构建了向量自回归（VAR）模型，研究了中国FDI 金额与人民币汇率之间关系，格兰杰（Granger）因果检验表明它们存在双向因果关系：一方面，FDI 流入促使了人民币升值；另一方面，人民币升值也吸引了FDI 增加。

3 计量模型与方法

为人民币汇率形成机制可能存在的非线性效应及其中的异质作用机制，建立神经网络分位数回归（QRNN）模型，一方面通过NN 模型模拟人民币汇率的非线性形成机制，另一方面通过QR模型揭示人民币汇率整个条件分布的异质性与变动规律。

基于人民币汇率影响因素分析，本文以人民币汇率（ER）为输出变量，以出口（EX）、进口（IM）、外汇储备（FER）、广义货币（M2）、居民消费价格指数（CPI）、外商直接投资（FDI）、银行同业拆借利率（LIBOR）等为输入变量，建立QRNN 模型。为了消除趋势因素的影响，本文对上述变量分别实施自然对数变换。

（1）人民币汇率的QRNN 模型

这里采用三层感知器结构，以响应变量ERt作为输出层，以解释变量向量Xt=(FERt,M2t,CPIt,IMt,EXt,FDIt,LIBORt)' 作为输入层，建立一个神经网络模型。进一步，考虑解释变量对响应变量条件分布的影响，建立QRNN 模型如下

在QRNN 模型中，当K=1 且f(h)(·)和f0()(·)都为等值函数时，该模型退化为一个线性分位数回归（QR）模型。此外，NN 模型就是QRNN 模型在τ＝0.5 时的特例。由此可见，QRNN 模型是一个包容性较强的模型。

综合式(1)和(2)，可以得到，输出层与输入层之间存在着非常一般的非线性关系

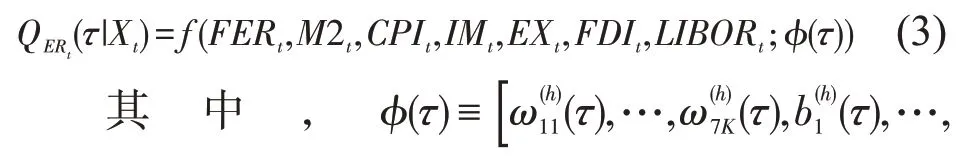
其中，T为样本量。

Cannon[27]指出，可以在上述目标函数中引入一个惩罚项，以避免QRNN 模型的过度拟合问题。因此，为实现QRNN 模型估计，可以转化为一个优化问题

许启发等[17]指出，在实际应用中，惩罚参数λ和隐含层节点数K的最优取值可以通过AIC 准则来实现：

其中，F-1(τ)≘Q(τ)为F的第τ分位数。由式(7)，可以看到，概率密度函数可以由分位数曲线的徽商倒数获得。因此，对式(7)分别进行条件化和离散化两步操作，就可以实现对ERt进行条件概率密度预测，得到。

4 实证研究

（1）样本数据选取

考虑到中国人民银行在2010 年6 月19 日重启汇率改革，本文选取2010 年7 月至2014 年12月为样本区间，以月度人民币汇率数据为研究对象。其余变量也是月度观测频率。所有样本数据分别来源于中国人民银行网站、中国外汇交易中心网站、国家统计局网站与国际货币基金组织网站等。为建立QRNN 模型，将整个样本区间划分为两个部分：第一，样本内数据包括2010 年7 月至2014 年6 月，用于QRNN 模型估计；第二，样本外数据包括2014 年7 月至2014 年12 月，用于QRNN 模型预测。

（2）人民币汇率预测结果

本文主要使用QRNN 模型，预测人民币汇率的条件概率密度。为比较，进一步考虑了几个经典模型，主要包括：基于线性分位数回归（QR）模型的条件概率密度预测，基于BP 神经网络（BPNN）模型、线性均值回归（MR）模型的点预测。

第一，概率密度预测结果：以样本内数据为训练集，对QRNN 模型进行估计（训练），结果如表1所示：隐含层节点数，惩罚参数；限于篇幅，没有报告权重估计结果。运用估计的QRNN 模型，对测试集数据进行预测。图1 中，报告了人民币汇率的条件概率密度预测曲线（2014 年7 月至2014 年12 月），竖线为人民币兑美元汇率的实际值。

表1 神经网络分位数回归模型参数选择结果

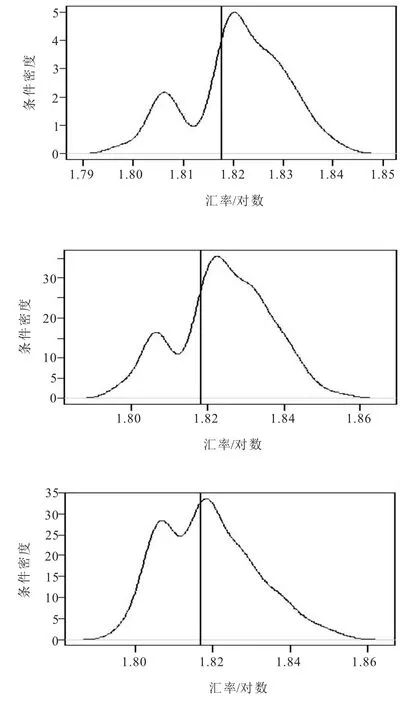
图1 基于神经网络分位数回归的人民币兑美元汇率概率密度曲线图

由图1 可知，使用QRNN 模型可以预测人民币汇率的完整条件概率分布信息。更进一步，在整个预测区间，概率密度曲线包含了人民币汇率实际值。此外，预测的中位数、众数等都与实际值较为接近，表2 的预测评价结果也证实了这一点。总之，QRNN 模型不但具有很高的预测精度，而且能够给出整个条件概率密度预测结果，包含了更多预测信息。

第二，点预测结果：为便于比较，本文还选取BPNN 模型、MR 模型等，对测试集的人民币汇率进行点预测，得到相应结果见表2。

根据QRNN 模型的隐含层节点数选取结果，这里将BPNN 模型的隐含层节点数也设置为5，其阈值设置为0.001。由表2 可知，BPNN 模型比MR 模型具有更小的预测误差，有更好的点预测结果。

3.预测结果评价

这里，比较分位数回归（QR）模型与均值回归（MR）模型的预测结果，可以发现QR 模型能够给出完整的条件概率密度预测结果，从而比MR 模型的点预测提供了更多有用信息。事实上，由概率密度预测结果，能够比较容易得到包含中位数与众数在内的点预测结果。根据统计学观点，中位数预测体现了“平均”含义，而众数预测则表示最可能发生的意义。在表2 中，同时报告了基于QR 模型的两个点预测结果，以及点预测与实际值之间的预测误差。由表2 可知，基于QRNN 模型的众数预测的平均绝对误差最小，只有0.2260%，其最大相对误差也只有0.3168%。这些结果表明，基于QRNN 模型的众数预测最为逼近人民币汇率实际值，意味着最可能发生的预测结果与最理想结果之间的一致性。

表2 预测值及预测误差

5 结论与启示

考虑到人民币汇率形成机制的非线性效应，本文结合分位数回归（QR）与神经网络（NN）模型两个方面的优势，建立QRNN 模型，实现人民币汇率条件概率密度预测。实证中，人民币兑美元汇率（ER）为输出变量，以出口（EX）、进口（IM）、外汇储备（FER）、广义货币（M2）、居民消费价格指数（CPI）、外商直接投资（FDI）、银行同业拆借利率（LIBOR）等为输入变量，建立了QRNN 模型以及其他多种模型，预测人民币兑美元汇率的条件概率密度并比较预测结果。实证结果表明：第一，QRNN 模型的两个点预测（包括：中位数预测与众数预测）结果非常接近人民币汇率的实际值，点预测效果明显优于QR 模型、BPNN 模型、MR 模型等；第二，QRNN 模型能够给出完整条件概率密度预测结果，从而提供人民币汇率未来变化及走势的丰富信息，便于进行科学决策，引导与建立合理的人民币汇率形成机制。