高超声速飞行器表面吸附特性对多相催化过程影响的数值模拟
2021-12-07杨肖峰杜雁霞
李 芹,杨肖峰,董 威,杜雁霞
(1.上海交通大学 机械与动力工程学院,上海 200240;2.中国空气动力研究与发展中心 空气动力学国家重点实验室,四川 绵阳 621000)
当飞行器在高超声速条件下再进入空气环境时,在激波压缩和黏性耗散的作用下,激波层内气体温度很高,可以达到 5 000 K,甚至更高,空气中的N2和O2会发生不同程度的离解和电离.离解的原子将在表面材料的催化下发生复合反应,反应释放的热量在气动热中占比高达30~50%[1-2].这类由固相材料作催化剂的气相原子复合反应属于多相催化.
根据多相催化反应动力学,高焓离解气流在气固界面将发生扩散、吸/解附及复合等一系列行为.气相原子扩散至表面后,首先在有限数密度的吸附位点上发生物理(被吸附原子与吸附位点粒子以分子间作用力束缚)或化学(二者之间形成化学键)吸附.吸附相原子与气相原子结合或两邻近吸附相原子相结合,即发生Eley-Rideal(ER)或Langmuir-Hinshelwood(LH)复合反应,产生大量反应热.
基于催化反应边界模型的计算流体力学(CFD)方法是预测高超声速飞行器催化加热的重要研究手段之一.然而,采用不同壁面催化模型得到的热流预测偏差高达2~4倍[3],给飞行器防热设计与评估带来很大的不确定度[4-5].因此,迫切需要发展具有物理意义的有限速率壁面催化模型,进而获得准确有效的催化加热预测结果.目前常用的有限速率催化模型是基于多相催化反应动力学,根据实验数据拟合建立各反应速率与表面温度的关联,即现象学模型[1,6-7].
基于此类模型,诸多学者开展了大量由ER复合[8-10]和LH复合[1,11-12]主导的多相催化CFD模拟.上述研究中,在较低壁温(Tw<1 000 K)条件下,气相原子与吸附相原子碰撞概率大,通常忽略物理吸附和LH复合,仅考虑基于化学吸附作用的ER复合过程;而在较高壁温(Tw>1 000 K)条件下,因吸附位点间原子迁移和碰撞更活跃,更多地考虑LH复合过程[11,13].但是,微观尺度的理论模拟研究发现,LH复合不仅发生在较高温度段,在较低温度段内因物理吸附作用的参与而同样重要.
针对上述壁面反应机理,Norman等[14-15]重点考虑高温和低温条件下化学和物理吸附作用,建立了含物理吸附和LH复合的有限速率壁面催化模型.Li等[16]进一步集成Norman团队的高、低温模型,建立了全温度范围内与实验数据吻合的四步模型.尽管上述研究揭示了较宽温度段同时考虑ER和LH的催化反应机理,但是涉及的有限度率模型尚未直接应用于飞行器绕流流场的CFD模拟中,更难以获得特定材料表面原子吸附特性对多相催化和流动传热过程的影响规律.
针对上述问题,本文通过考虑物理吸附以及物理吸附原子与化学吸附原子间的LH复合作用,发展了可用于CFD模拟的有限速率四步催化模型,并参数化分析了物理和化学吸附位特性对高超声速飞行器表面多相催化过程的影响规律.相关研究结果可以为高超声速飞行器气动热环境精细化预测、热防护系统设计及评估提供理论支撑.
1 黏性壁面边界模型
1.1 有限速率四步催化模型
传统的三步催化模型包括表1中的反应1,3,4,可有效预测高壁温条件下表面催化系数和气动加热.表中“A”代表气相原子;“s”代表化学吸附位点;“f”代表物理吸附位点;“A(s)”和“A(f)”分别代表物理吸附原子和化学吸附原子.本文进一步考虑物理吸附以及物理吸附原子与化学吸附原子之间的LH复合反应,发展了可用于CFD黏性壁面边界表征的有限速率四步催化模型,涉及的表面反应包括表1中的反应1,2,3,5.反应5与反应4的本质区别在于以分子间作用力束缚在表面吸附位点的原子A(f)发生表面迁移、碰撞及复合的反应能垒较低,因此用于表征较低壁温条件下的催化反应过程.

表1 表面催化的多步反应过程Tab.1 Multi-step reaction processes of surface catalysis
1.2 边界质量平衡条件
气/固界面上的质量平衡方程是表面催化模型与流场控制方程Navier-Stokes(N-S)方程的求解实现耦合的枢纽.由于激波层内的流场包含化学反应,描述该流场的N-S方程组中包含各组分的质量守恒方程,因此需要给定流场域边界(即气/固界面)上的组分条件.该条件通过气/固界面上的质量平衡方程给定.在稳态条件下,由浓度梯度驱动而扩散至表面的组分A质量通量与通过表面催化反应消耗的组分A质量通量达到平衡,即
(1)

1.3 O原子反应速率确定方法
表面多相催化各过程(吸附、ER及LH复合)的反应速率由各反应物浓度及反应速率常数确定,具体表达式如下:
(2)
(3)
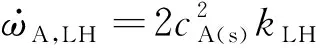
(4)
(5)
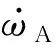
2 数值方法
高超声速非平衡流场计算基于空气动力学国家重点实验室FL-CAPTER软件平台[17].使用总变差减小(TVD)格式的有限体积法对N-S方程进行离散.在空间方向上,对无黏通量采用二阶van-Leer矢量通量分裂法离散,黏性通量采用中心格式离散,界面通量用MUSCL方法进行插值.在时间方向上,采用LU-SGS隐式方法推进,直至流场达到稳定.
2.1 催化模型与流场求解器的耦合
表面有限速率四步催化模型与N-S方程求解器之间的耦合通过边界质量平衡方程实现,耦合求解流程如图1所示.首先,将各步反应的速率常数和气相及吸附相反应物浓度代入表面催化反应模型,求得边界上由催化反应导致的各组分质量通量.其次,将边界上的反应通量与扩散通量守恒方程作为组分边界条件,与N-S方程形成封闭的控制方程组.最后,求解该方程组得到流场中的组分浓度、压力、速度及温度分布,其中组分浓度作为催化模型中的气相反应物浓度输入条件,提供给下一次迭代.
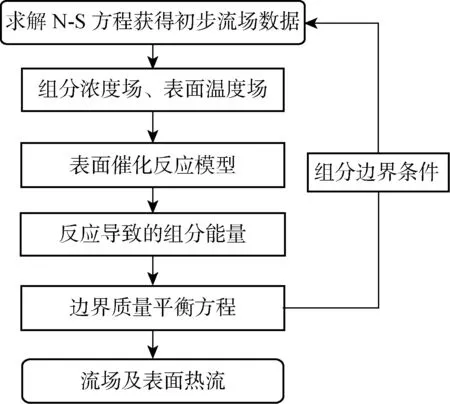
图1 催化模型与N-S方程的耦合求解流程Fig.1 Coupling procedure of N-S equations solver and catalytic model
2.2 数值方法验证
为了验证数值方法流场求解的有效性,采用Karl等[18]针高超声速圆柱绕流的哥廷根高能激波风洞(HEG)实验进行算例验证.圆柱模型半径为45 mm,展向具有较好的二维效应.研究使用的来流条件与文献[18]中算例627的条件相同,来流中包括N2、O2、NO三种分子组分和N、O两种原子组分,见表2,表中w为气相组分的质量分数.壁面取恒定壁温条件Tw=700 K.计算网格为100(周向)×150(法向)的六面体多块结构化网格,如图2所示,图中s为圆柱表面周向距离,α为周向长度对应的角度.空间网格无关性验证如图3所示,横坐标X*为以圆柱半径R为参考长度的无量纲X方向距离,纵坐标ρ*为以来流密度ρ∞为参考值的无量纲密度.结果表明,当采用100×150的网格时,可以准确捕捉激波位置,而当网格进一步加密时激波位置变化极小.壁面法向网格的无关性分析如图4所示,s*为以圆柱半径R为参考长度的无量纲周向距离,Q为气动热,Recell为壁面法向第一层网格的网格雷诺数.壁面法向第一层网格厚度取d1=10 μm(Recell=4.6)时,可网格无关地模拟出壁面热流.

表2 验证算例的来流条件Tab.2 Inflow conditions for validation case
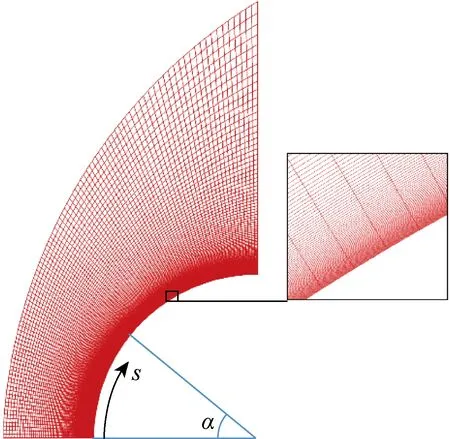
图2 圆柱高超声速绕流的流体域网格(网格节点数:100×150,Recell=4.6)Fig.2 Grids in fluid domain for hypersonic flow over cylinder (Grids:100×150,Recell=4.6)
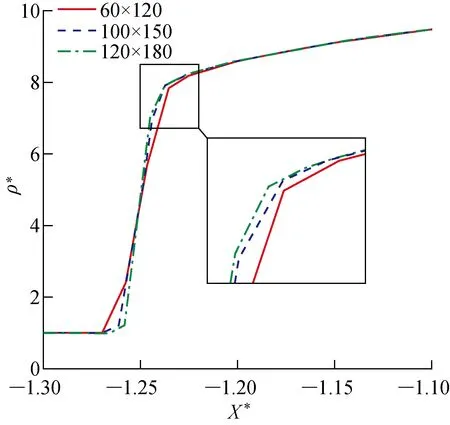
图3 网格数量对滞止线上无量纲密度的影响Fig.3 Influence of grid refinement on dimensionless density of stagnation line

图4 壁面第一层网厚度对驻点热流的影响Fig.4 Influence of height of first cell on stagnation heat flux
实验采用全息图像重建方法得到了用于表征流场密度和组分变化的相移:
(6)
式中:λ为测试设备发射的激光波长;z为圆柱模型的展向长度;Ki为各个组分的计算系数,其取值见文献[18].本研究获得的相移模拟云图与Karl等的实验对比结果如图5所示,图中Y*为以圆柱半径为参考长度的无量纲Y方向距离.可以看出,流场求解器捕捉的激波位置与实验激波位置重合,激波层内相移分布基本一致,仅在驻点周围的壁面附近处有细微差异,说明非平衡流场求解器FL-CAPTER对高超声速圆柱绕流的非平衡流场预测是可靠的.
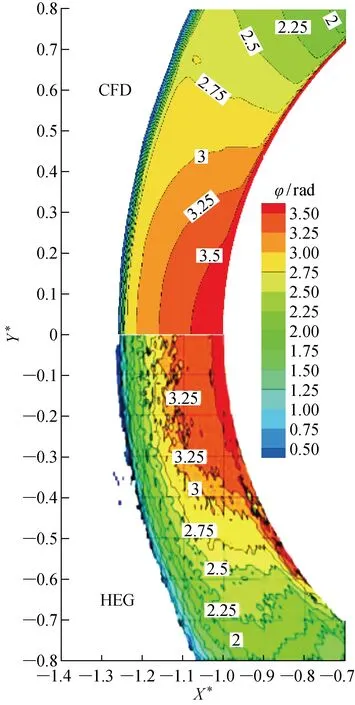
图5 CFD计算的相移与HEG实验结果对比Fig.5 Comparisons of phase shift contour of CFD and result of HEG experiment
为了验证催化模型对气动热求解的有效性,采用美国LENS激波风洞高超声速圆柱绕流实验[19]进行了算例验证,圆柱模型直径44.5 mm,来流条件与文献[19]中的RUN75相同.计算中物理和化学吸附位的数密度取1018/m2,N、O原子物理/化学吸附的反应速率常数取1.0,物理/化学吸附位覆盖率取0.02,ER复合的反应速率常数取0.05,LH复合的反应速率常数取0.001.
分别采用完全催化模型(FCM)、有限速率催化模型(FRCM)及完全非催化模型(NCM)获得了表面的热流分布,与不同实验测试手段测量的3组热流分布(实验数据1~3)对比,结果如图6所示.结果表明,四步有限速率催化模型(FRCM2)预测的气动热处于非催化与完全催化模型所预测的气动热之间,符合物理规律.当前参数取值下的有限速率催化模型预测的气动热与实验通过不同测试方法获得的气动热吻合较好,与保守地采用完全催化模型或人为给定净催化系数相比,模型能够更准确有效地预测非平衡流场中催化壁表面的反应和传热过程.除此之外,图6中还给出了传统只考虑化学吸附的模型(FRCM1)获得的表面气动热预测结果.传统的三步催化反应模型认为,表面温度低于 1 000 K时LH复合难以被激发,而本算例表面温度为300 K,因此LH复合可以忽略,即传统模型此时变为包含化学吸附和ER复合的两步反应模型.可以看出,四步催化反应模型预测的气动热略高于实验值,而传统只考虑化学吸附的模型预测的气动热略低于实验值.尽管两模型对气动热的预测精度相似,但是四步反应模型由于包含的反应机理更丰富而且更能体现表面真实的物理化学过程.
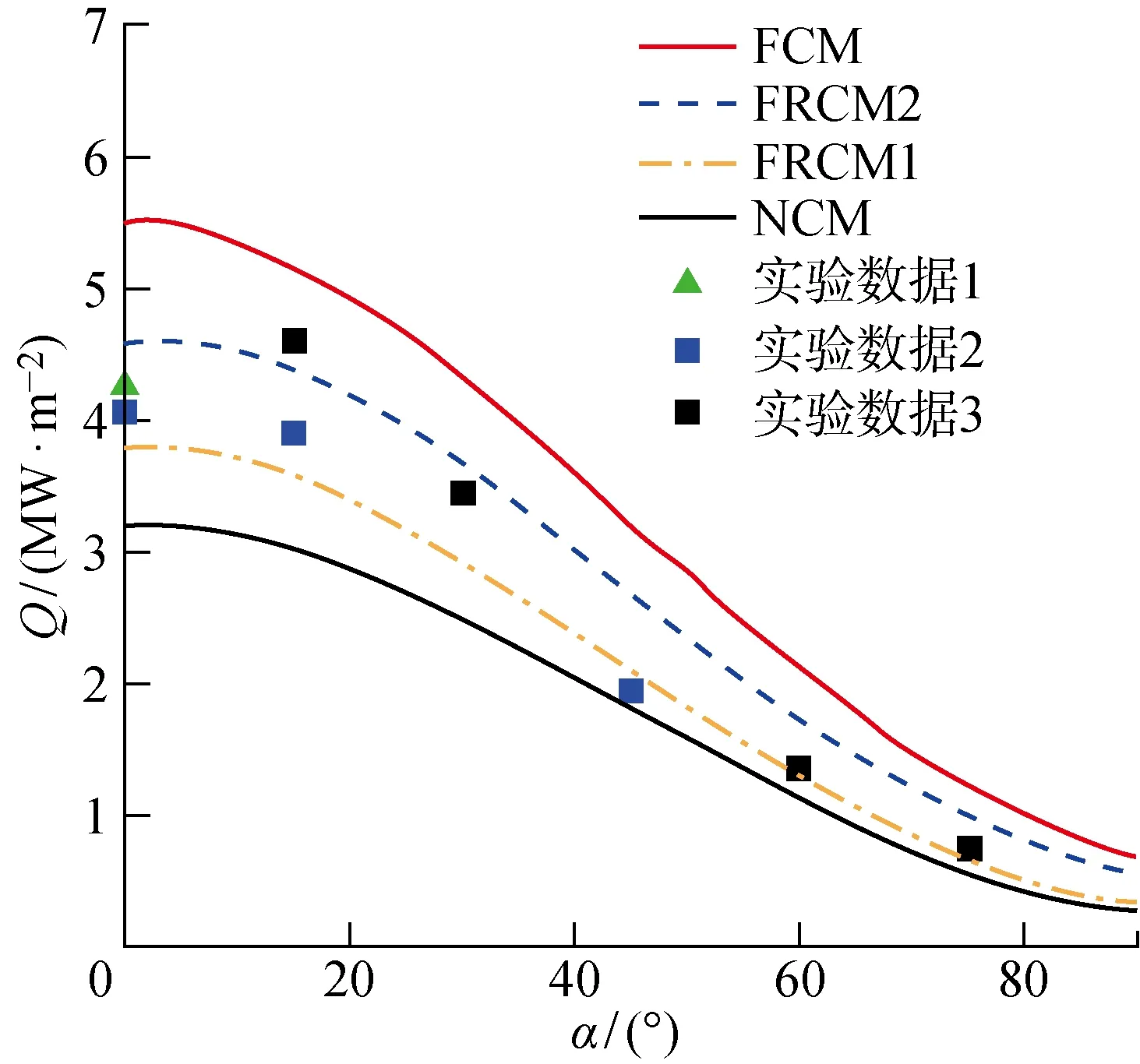
图6 完全催化、有限速率催化及完全催化模型预测的圆柱表面气动热Fig.6 Aerodynamic heat of cylinder surface predicted by full-catalytic,finite rate catalytic,and non-catalytic model
此外,当以非催化表面获得稳定的流场后,再分别采用两种有限催化模型进行气动热的预测.图7给出了两步催化模型和四步催化模型下圆柱驻点热流Qstag随迭代步数N的变化.而图8是残差随迭代步数的变化,图中Rρ*为无量纲密度ρ*的二范数残差.可以看出,增加反应步骤对计算收敛速度的影响不大,因此尽量将目前对催化反应机理的认识写入边界条件模块,在提高表面气动热预测精度的同时,不会大幅增加计算成本.
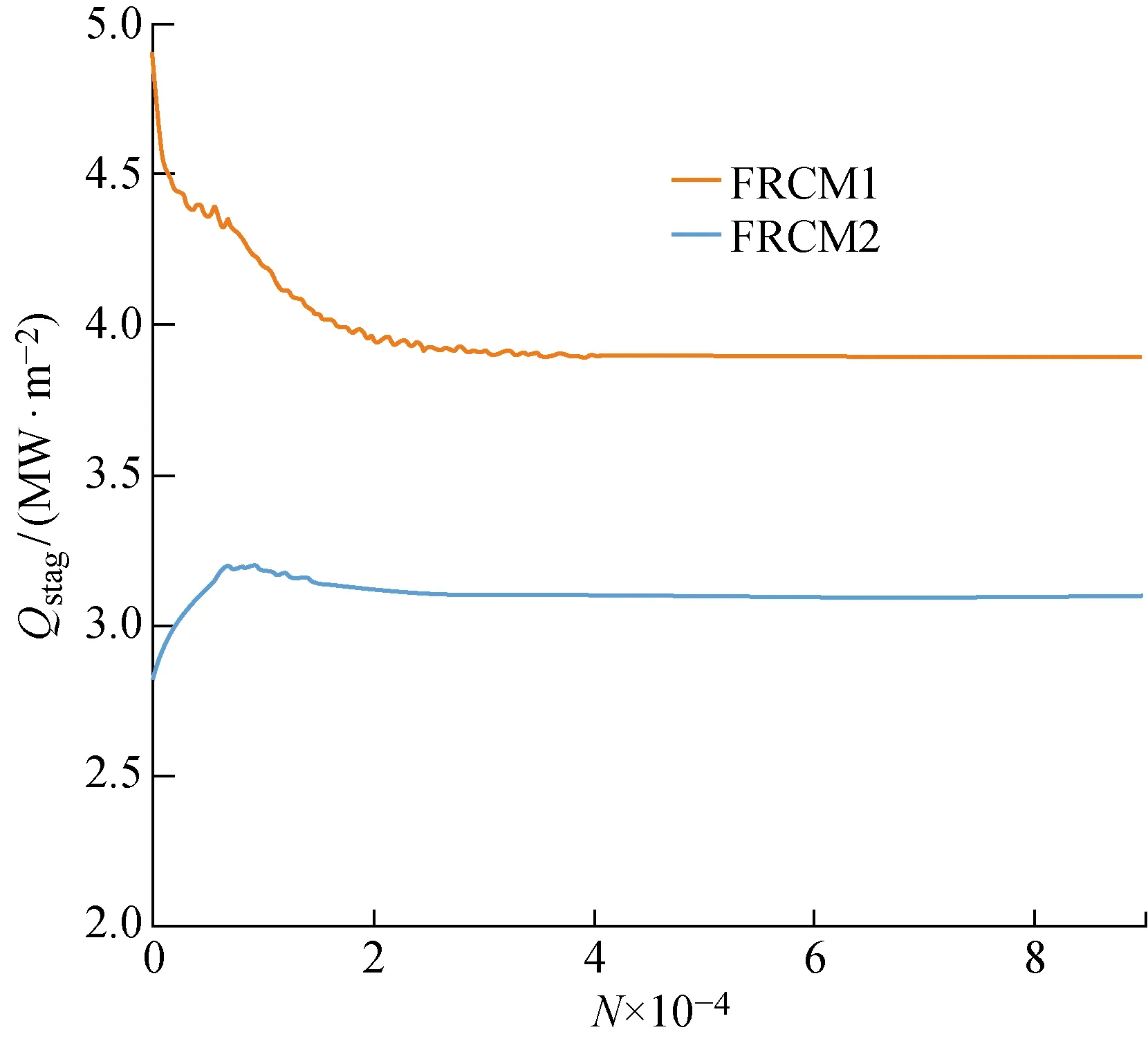
图7 驻点热流随迭代步数的变化Fig.7 Heat flux at stagnation point versus number of iteration steps
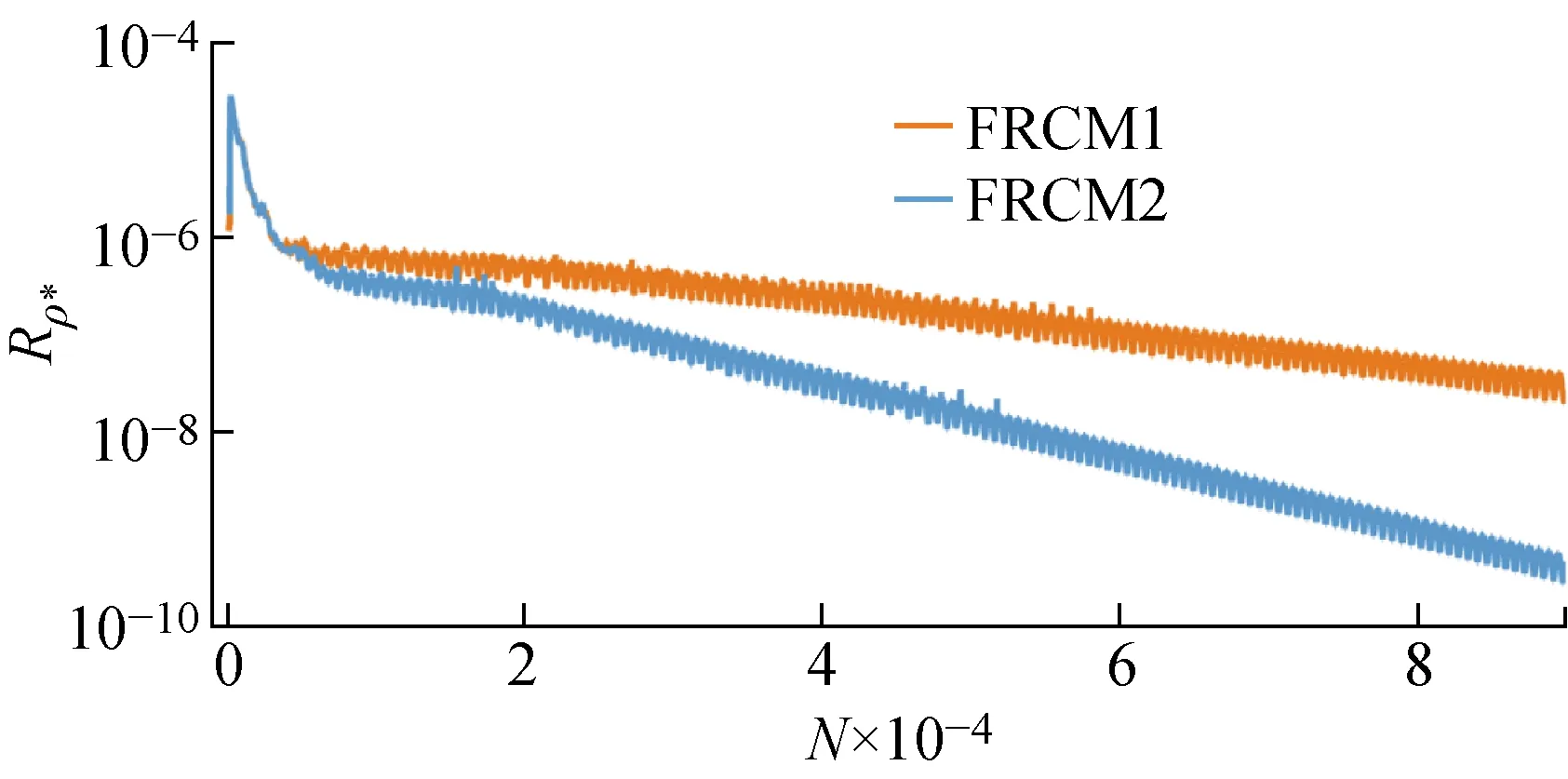
图8 无量纲密度的残差曲线Fig.8 Residual curves of dimensionless density
3 结果与分析
由于表面的物理和化学覆盖率无法通过宏观方法获得,但是这些参数受表面材料属性和温度影响很大,进而对催化反应和气动加热产生影响,因此通过参数化方法来分析化学吸附位覆盖率及物理吸附位覆盖率对N、O原子的催化效率及催化加热量的影响.针对化学/物理覆盖率的计算条件设置见表3,算例01~04用于比较O原子的物理吸附位覆盖率FO对催化反应的影响,算例01、05~07则用于比较O原子的化学吸附位覆盖率SO对催化反应的影响.每个算例中N原子和O原子的物理/化学吸附反应的速率常数假设为1,N原子的物理吸附位覆盖率FN及化学吸附位覆盖率SN都假设为0.1,化学和物理吸附位数密度取1018/m2.ER复合的反应速率常数设为0.05,LH复合的反应速率常数设为0.001.物理模型与2.2节相同,来流温度、压力及速度条件见表2,而O2和N2的质量分数分别为0.77和0.23.
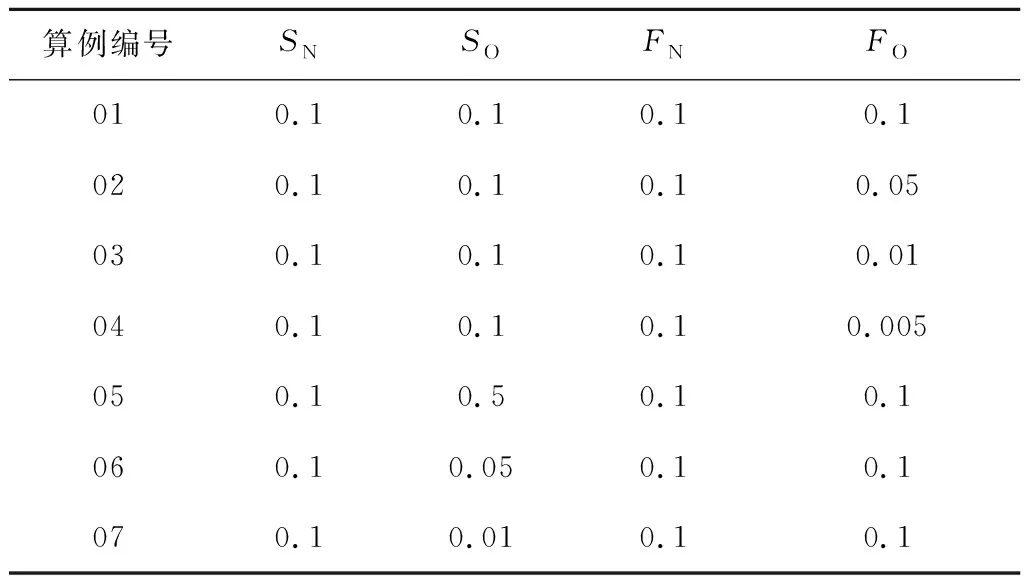
表3 算例物理、化学吸附位覆盖率条件设置Tab.3 Settings of fraction of occupied physisorption and chemisorption sites
3.1 流场与气动加热特征
以算例01为例说明圆柱非平衡绕流流场和表面气动加热的分布特征.在该来流条件下圆柱前部流场形成弓形激波,激波层内温度T、压力p迅速上升,如图9所示.激波后的O2和N2发生部分离解,并在激波后强非平衡区产生一定的NO,组分沿驻点线的分布如图10所示.
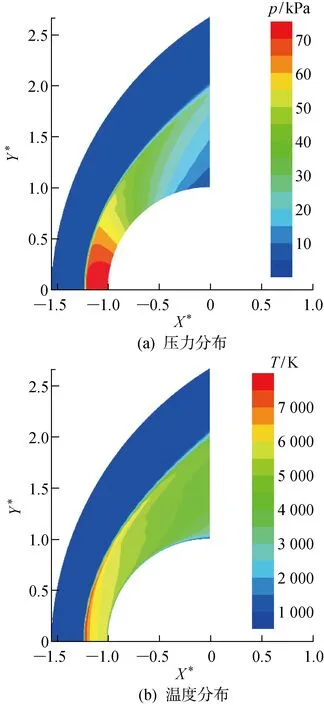
图9 圆柱模型高超声速绕流流场的特征Fig.9 Characteristics of flow field around a cylindrical model with hypersonic flow
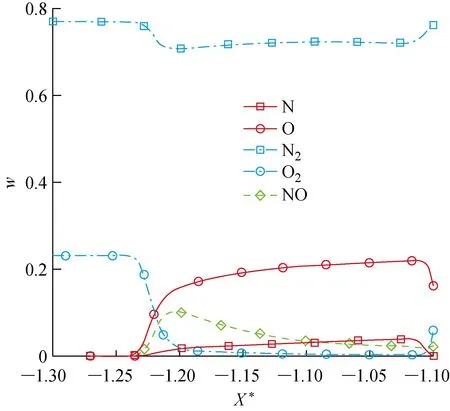
图10 驻点线上各组分的质量分数(X*=-1为驻点)Fig.10 Mass fraction of each species along stagnation line (X*=-1)
由于N2发生离解的温度较高,因此目前计算条件下气相N原子含量较少,这导致表面气动热大部分由对流加热和O原子的复合放热组成,N原子的复合放热接近0,如图11所示.而且在不同算例中,对流加热量变化不大,所以算例之间Q的相对大小由O原子复合放热量QO决定.因此在3.3~3.4节的对气动加热的分析中只研究物理/化学吸附位覆盖率对O原子所参与反应的影响.
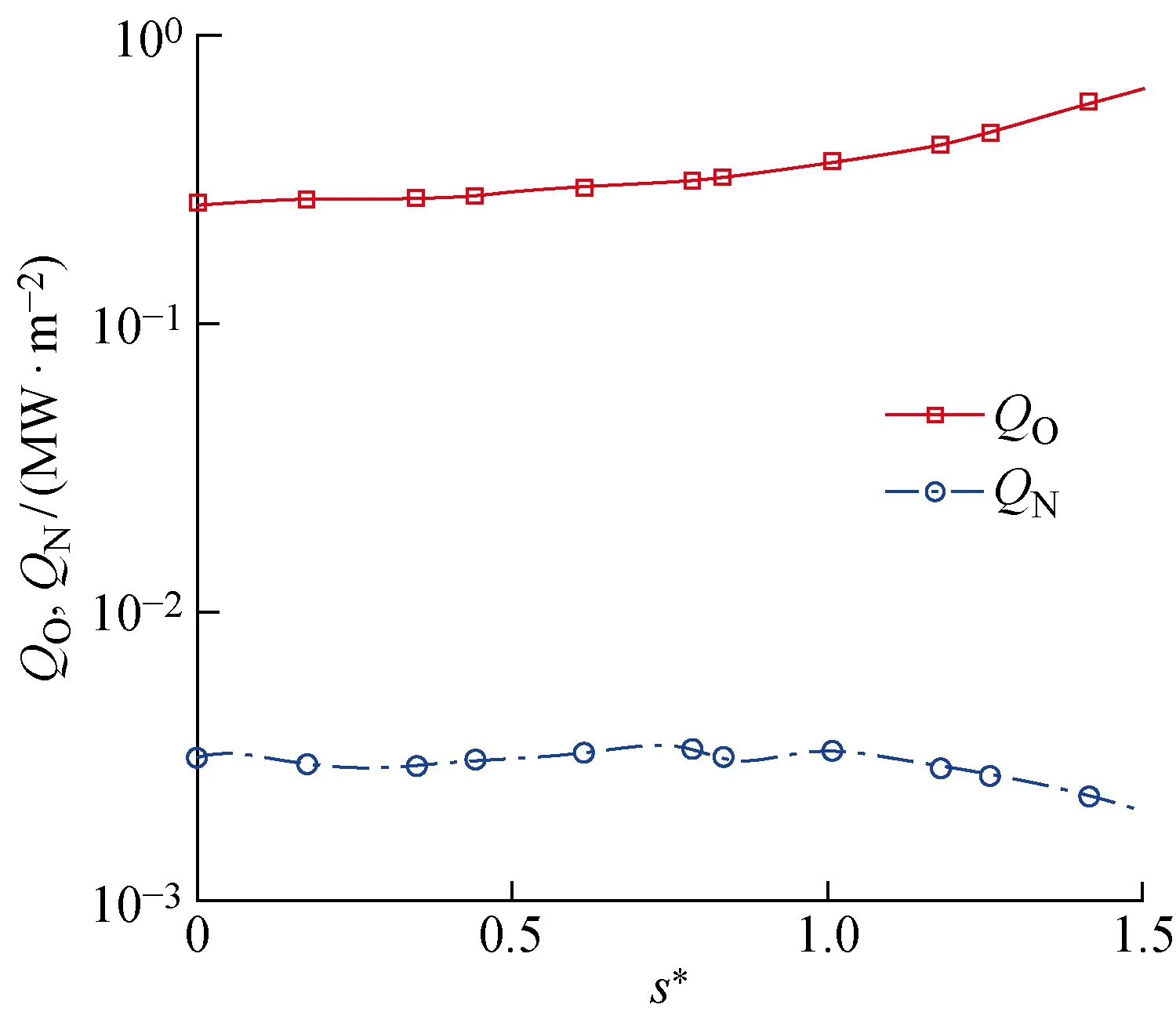
图11 O原子、N原子催化复合导致的气动热Fig.11 Aerodynamic heat caused by catalytic recombination of O atoms and N atoms
3.2 物理吸附位覆盖率对催化过程的影响
通过参数化地分析物理吸附位覆盖率对O原子消耗速率的影响,来研究其对催化过程的影响.图12、13分别给出了不同物理吸附位覆盖率条件下LH和ER复合反应导致的圆柱表面O原子消耗速率,图中mO,LH、mO,ER分别为LH及ER复合反应导致的单位时间内、单位面积上氧原子的消耗速率.可以看出,LH反应的速率整体上随着物理吸附位的覆盖率FO增大而增大,这是因为FO增大即吸附相O(f)的质量分数增加,O(f)作为LH复合反应的反应物之一,加速该反应对O原子的消耗.而ER复合反应速率随FO的增大而减小,呈现出与LH复合相反的变化规律.在研究的物理、化学吸附位覆盖率范围内,头部催化反应以ER复合为主导,尾部则出现LH反应加快及ER反应减慢的现象,导致尾部以LH反应为主导.由于LH反应速率的增幅比ER反应速率的降幅小,所以两者共同导致的O原子总消耗速率随FO的增大而增大(见图14).
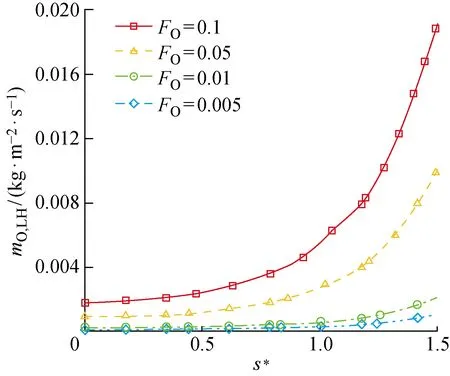
图12 LH复合反应导致的圆柱表面O原子消耗速率Fig.12 Consumption rate of O atoms caused by LH recombination
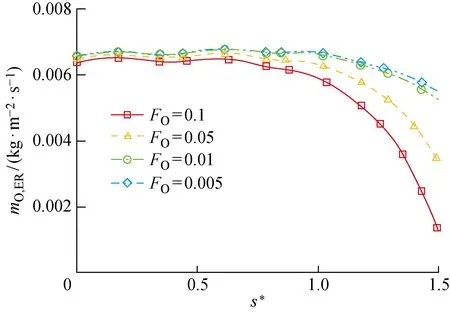
图13 ER复合反应导致的圆柱表面O原子消耗速率Fig.13 Consumption rate of O atoms caused by ER recombination
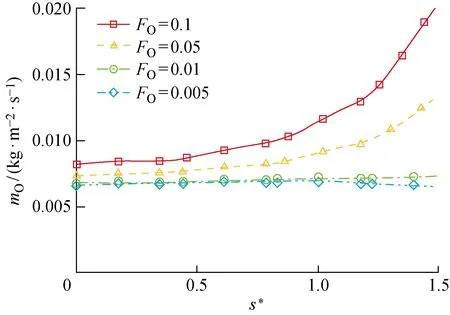
图14 催化反应导致的圆柱表面氧原子消耗速率Fig.14 Consumption rate of O atoms caused by catalytic reaction
虽然O(f)并不直接参与ER复合反应,但是通过反应之间的互相影响限制了ER复合.当FO增大时,LH复合加速,因此对O(f)和O(s)的消耗加快,表面物理和化学吸附空位浓度增加,促使物理和化学吸附过程加速.由于激波后气体环境中离解生成的O原子数量一定,边界上物理和化学吸附反应的加速使得边界上气相O原子质量分数wO降低(见图15),而气相O原子是ER复合反应的反应物之一,因此ER复合反应速率受到限制.
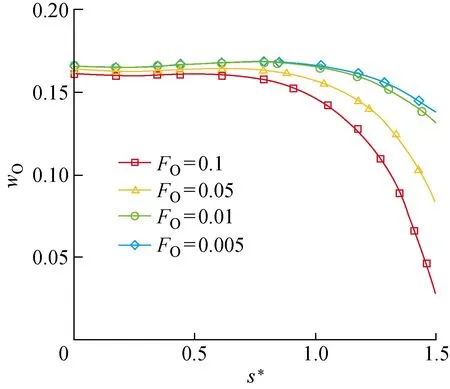
图15 壁面上的O原子质量分数随FO的变化Fig.15 Mass fraction of O atoms along surface versus FO
此外,沿圆柱表面周向,LH复合反应增加,ER复合反应减小,头部与尾部最大可相差10倍左右.由于尾部气相O原子质量分数显著降低,ER反应随之减缓,ER反应对化学吸附相氧原子O(s)的消耗减缓,因此有更多的O(s)可以用于LH复合反应,使得尾部LH复合反应显著加快.
与上述分析的物理吸附位覆盖率对O原子总消耗速率的影响相似,表面气动热随物理吸附位覆盖率的增大而增加,如图16所示.
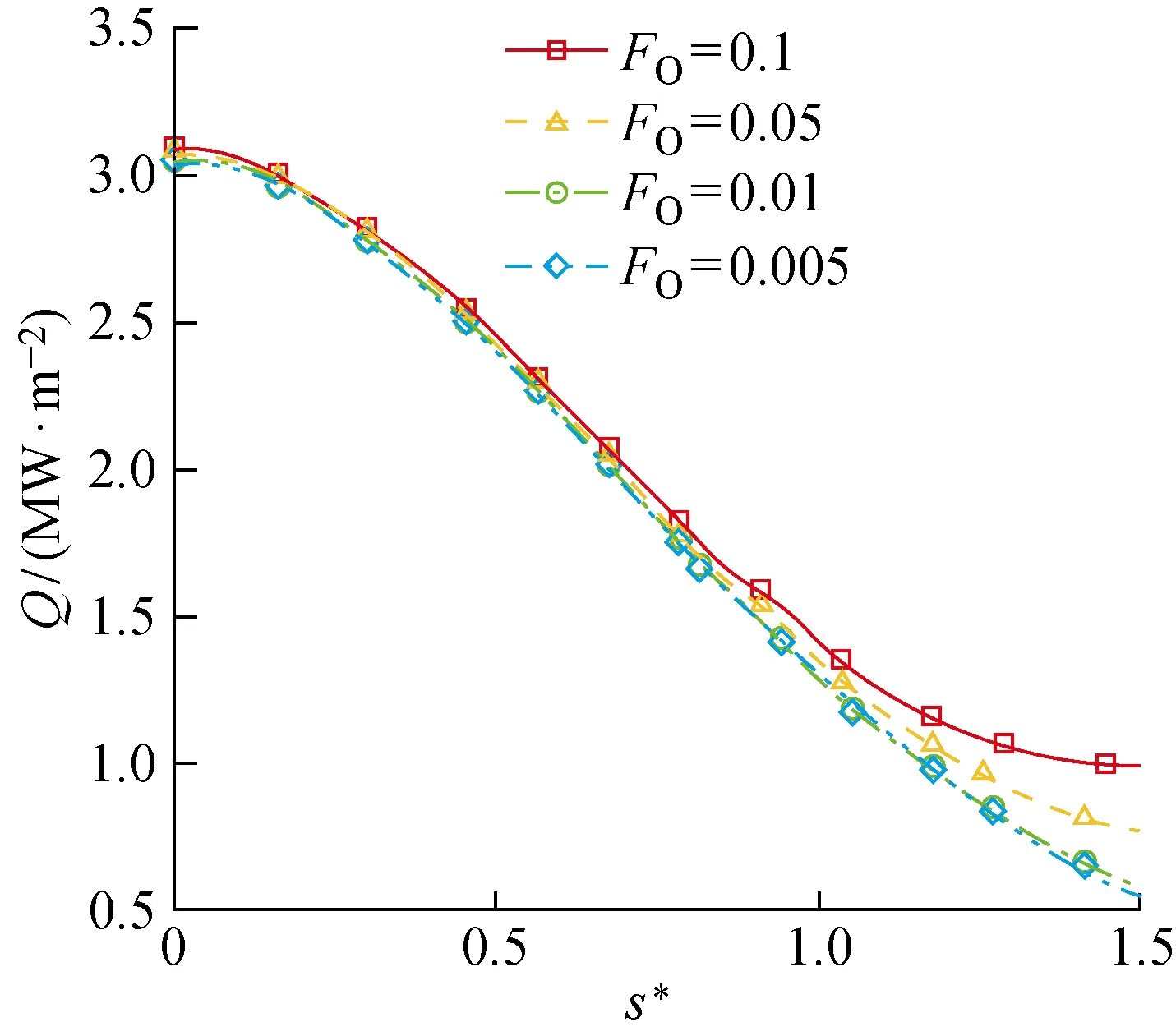
图16 FO对圆柱表面气动热分布的影响Fig.16 Influence of FO on aerodynamic heat flux distribution on cylinder surface
3.3 化学吸附位覆盖率对催化过程的影响
进一步通过同样的参数化分析,来研究化学吸附位覆盖率对催化过程的影响.如图17、18所示,整体而言,ER、LH复合反应速率随O原子对化学吸附位的覆盖率SO的增大而增大,因为两种复合反应中,化学吸附相O(s)都作为其中一个反应物参与反应.与之对应,两种复合反应导致的氧原子消耗总速率也随SO的增大而增大,如图19所示.但是,由于在尾部激波强度变弱,激波层内气体温度相较于驻点邻近偏低,所以O2的离解程度更低,即气相O原子质量分数偏低(见图20),这导致ER复合反应的速率受到气相O原子质量分数的限制,在尾部逐渐减小.而对于LH反应,尾部ER反应的变缓为其提供了更多的化学吸附相O原子,所以LH反应速率在尾部反而逐渐增加.例外的是,在SO=0.5时,上游ER和LH复合的高反应速率造成尾部的O原子质量分数过低,进而限制了吸附反应的速率,导致表面吸附相浓度出现降低,所以SO=0.5时LH复合反应速率在尾部不增反降来保证SO=0.5不变.
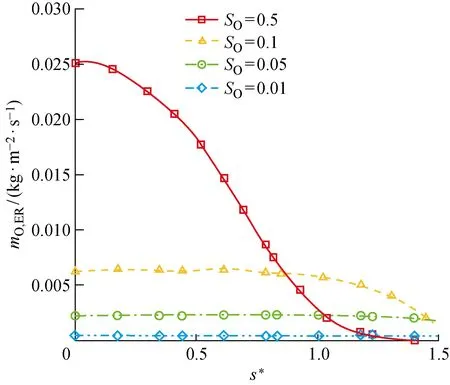
图17 ER复合反应导致的圆柱表面O原子消耗速率Fig.17 Consumption rate of O atoms on cylindrical surface caused by ER recombination

图18 LH复合反应导致的圆柱表面O原子消耗速率Fig.18 Consumption rate of O atoms on cylindrical surface caused by LH recombination
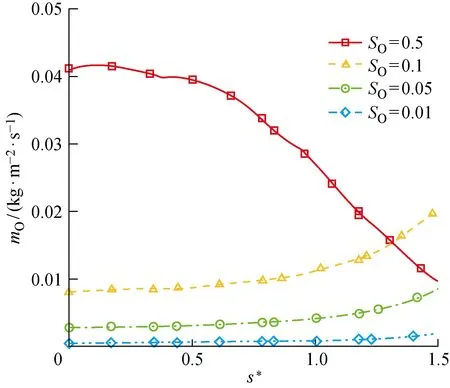
图19 催化反应导致的圆柱表面O原子消耗速率Fig.19 Consumption rate of oxygen atoms on cylindrical surface caused by catalytic reaction
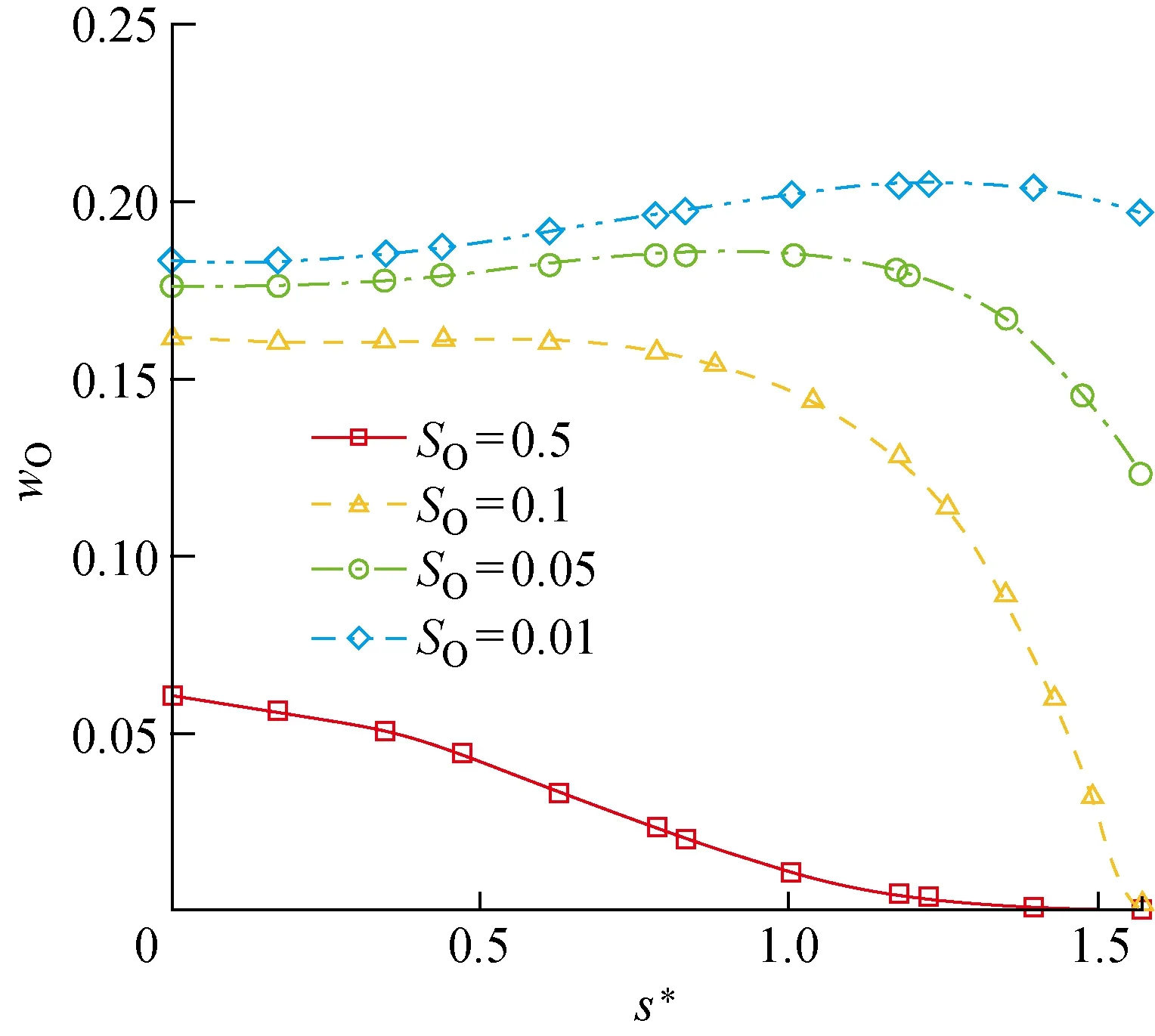
图20 流体域壁面边界上的O原子质量分数随SO的变化Fig.20 Concontration of O atoms on boundary of fluid domain versus SO
此外,尽管随着SO增大复合反应的速率增加,气相O原子质量分数降低,但是ER复合反应的速率并未出现降低(SO=0.5时的尾部速率除外).这说明在所研究的组分浓度和化学吸附位覆盖率范围内,ER复合反应的速率主要受到化学吸附相O(s)的控制,且吸附反应的速率足够高,在低O原子质量分数下也能够维持表面覆盖率SO不降低.SO=0.5时,上游的反应速率过高造成的下游气相O原子质量分数降低足够明显,使得化学吸附反应速率降低至不能维持原有表面覆盖率的水平,所以ER反应必须相应地减缓来维持SO=0.5.
图21所示为表面气动热Q随化学吸附位覆盖率的变化规律与O原子总消耗速率随化学吸附位覆盖率的变化规律相似,Q随SO的增大而增加,而当SO增加至0.5时,由于气相O原子质量分数的降低,尾部Q出现下降.
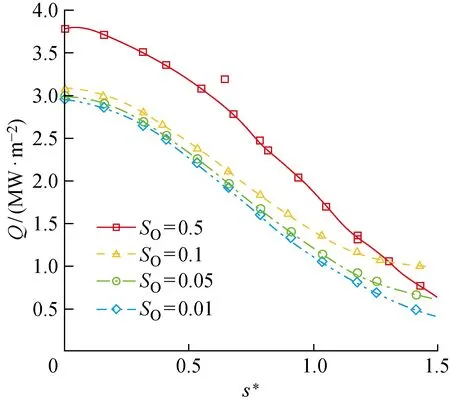
图21 SO对圆柱表面气动热分布的影响Fig.21 Influence of SO on aerodynamic heat flux distribution on cylinder surface
4 结论
本文发展了考虑物理吸附及物理吸附相原子参与复合的有限速率四步催化模型,并与CFD求解器耦合,参数化分析了物理和化学吸附位覆盖率对高超声速流场气/固界面上多相催化和气动热的影响规律.主要结论如下:
(1)有限速率四步催化模型基于表面物理化学过程得到催化反应速率,具有表征材料表面催化属性的真实物理意义,可以有效预测表面气动热.
(2)表面物理/化学吸附过程通过改变吸附相原子和气相原子的浓度来影响ER和LH复合过程,进而造成对表面气动热的影响,且由于各吸附、复合反应过程的交叉影响,气动热随表面覆盖特性的变化具有非线性特征.
本文所发展的四步模型可用于飞行器表面气动热的预测,且预测结果可以体现材料催化属性的差异,可为高超声速飞行器热防护系统的轻量化及低冗余设计提供理论支撑.
