重载机车车轮磨耗演化对轮轨接触关系的影响

郝 凯，刘鹏飞，王 晨，刘晓东，王晨龙

(1.石家庄铁道大学 机械工程学院，河北 石家庄 050043；2.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，河北 石家庄 050043)

0 引言

六轴重载机车是我国繁忙干线上的主要牵引装备，具有轴数多、轴距长、功率大的特点。随着运行里程的增加，不同车轮型面有着不一样的磨耗演化规律，磨耗型面与钢轨匹配对应车辆振动性能下降。车轮出现严重磨耗情况下，甚至可能发生列车脱轨事故[1-2]。因此，有必要对重载机车磨耗后轮轨接触匹配关系进行专门研究。

国内外针对轮轨接触关系进行大量研究，发现磨耗车轮型面轮轨接触具有很强的非线性，且研究对象多为高速动车。文献[3]分别将高速车轮原始型面和磨耗型面与钢轨匹配分析，研究轮对内侧距和摇头角对轮轨接触几何关系影响。文献[4]对高速车进行弹性化处理，分析轮对内侧距和轨底坡对轮轨磨耗影响。文献[2]针对高速铁路轮轨型面变化规律进行研究，分析钢轨和车轮磨耗特性及轮轨匹配等效锥度变化。文献[5]针对实测磨耗后车轮型面研究，指出设计新轮廓车轮型面，应考虑等效锥度、接触角和名义位置接触面积、接触应力和横向扩展之间的相互关系。文献[6]对高速车跨线运行时构架横向谐波振动显著增大进行分析，指出轮对横移量0～3 mm内等效锥度较大，提出钢轨打磨应避免钢轨轨顶位置差异过大，保证车轮踏面接触点位置一致。文献[7]指出等效锥度可以判断晃车和抖车现象，为轮对镟修和打磨提供合理的参考。以上文献对轮轨接触几何参数与轮轨型面匹配进行深入研究，将等效锥度限值标准应用到车辆运行管理中。重载机车车辆磨耗要比高速车磨耗量大，对六轴重载机车磨耗后轮轨匹配关系演化规律深入研究，有助于重载机车轮对服役时长的把控。鉴于此，搭建重载机车模型并对实测磨耗量与仿真结果进行验证，分析磨耗后轮轨型面匹配变化规律，为重载机车车轮维修提供参考。

1 机车模型搭建

1.1 车辆-轨道耦合动力学模型

基于车辆-轨道耦合动力学理论，建立HXD型六轴重载机车动力学模型，如图1所示。考虑中间轮对随横动自由移量变化的非线性特性，以及一系和二系减振器随振动频率变化的非线性特性[8]，分别采用bushing力元和Bipolar力元进行模拟。轨道模型选用移动质量钢轨模型，如图2所示，考虑钢轨横向、垂向移动以及纵向转动自由度。

图1 机车动力学模型

图2 移动质量钢轨模型

1.2 线路统计及仿真工况设置

对行驶在南同蒲线侯马—榆次线路重载机车，进行跟踪测试，获取到2.0、4.3、7.7万km车轮型面数据。该线路总长约300 km，线路多S弯，且部分区段钢轨有损伤，其中小半径曲线最多，统计如表1所示。为减小计算量，在仿真中进行简化处理，设置仿真曲线影响工况为曲线半径500 m，影响权重占比为10.7%。

表1 实测线路及仿真工况设置

1.3 磨耗仿真

车轮磨耗仿真流程如图3所示，基于重载机车动力学模型和移动质量钢轨模型，选用Kik-Piotrowski多点接触算法以及Archard磨耗模型对车轮磨耗演化仿真研究。初始轮廓配置为JM3车轮型面，配置曲线、直线轨道型面为CHN60，轨底坡选用1/40。从减小仿真计算量的角度，考虑磨损对称性，即前后转向架对称、左右车轮对称。

图3 车轮磨耗仿真流程图

1.4 波长等效法(UIC519)计算等效锥度

计算等效锥度有简化法、谐波法、线性回归法等，由文献[9]可知波长等效法(UIC519)最为准确，故选用该方法。在列车过曲线时，由向心力公式、牛顿第二定理及图4轮径与曲线半径关系，可得[7,9]

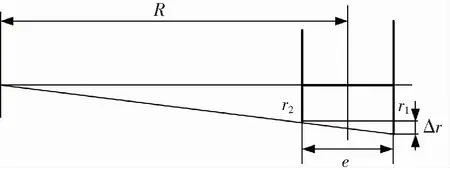
图4 轮径与曲线半径关系

(1)

式中，F为向心力;m为车辆质量;a为加速度;v为运行速度;R为圆曲线半径;e为接触点横向跨距;r1、r2分别为内、外侧车轮轮径;r0为车轮滚动圆半径;Δr为轮径差。

设速度v为常数，由v=dx/dt，推出

(2)

设车轮踏面外形为角度γ的锥形，可知Δr=2ytanγ，带入式(2)，可得常系数二阶微分方程

(3)

如图5所示，求得其解为波长λ的正弦波，化简可得等效锥度

图5 轮对运动轨迹波长

(4)

(5)

2 磨耗仿真验证及轮轨型面匹配分析

2.1 仿真与实测磨耗量对比

通过UM软件对数据处理，可得仿真与实测对比如图6所示。1～3位轮对轮缘最大磨耗量主要集中在-40～-30 mm位置，踏面最大磨耗量集中在20～30 mm位置，仿真与实测结果贴近，其中仿真轮缘磨耗量要比实测磨耗量靠右，有一定偏移量，可能是没有考虑钢轨与车轮接触弹性变形影响。1～3轮对在-20～40 mm位置，垂向磨耗量变化呈现正态分布，实测7.7万km下，2位轮对磨耗量要小于1、3位轮对，对比仿真结果，也是相应的变化规律。

图6 仿真与实测车轮型面及磨耗量对比

选取名义滚动圆位置处垂向磨耗量和轮缘最大磨耗量，作为车轮踏面和轮缘位置处评价指标。如图7、图8所示，仿真结果与实测结果相差不大。仿真分析运行里程2～8万km，1～3位轮对仿真踏面平均磨耗速率为0.197、0.222、0.199 mm/万km，实测数据为0.244、0.168、0.202 mm/万km，相差最大0.054 mm/万km；仿真获得最大轮缘平均磨耗速率0.379、0.278、0.279 mm/万km，实测数据为0.438、0.341、0.289 mm/万km，相差最大0.063/万km。对比仿真平均磨耗速率与实测结果相差较小，验证仿真模型的准确性。

图7 踏面名义滚动圆处磨耗量仿真与实测

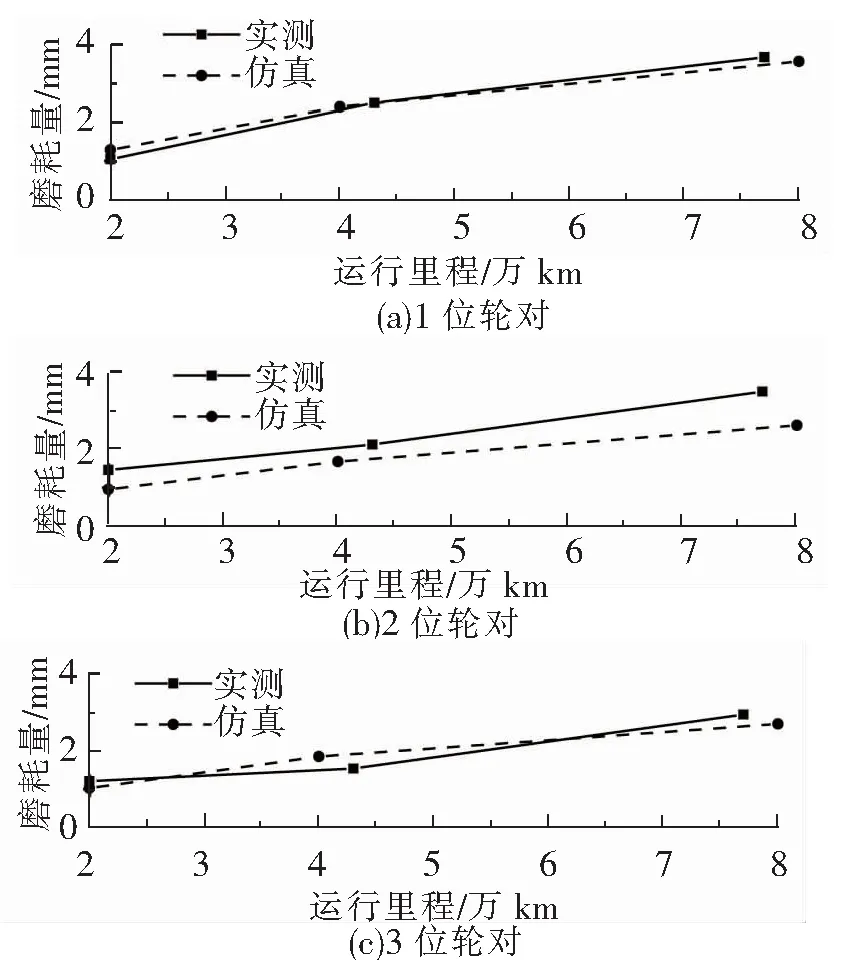
图8 轮缘最大磨耗量仿真与实测

2.2 等效锥度及磨耗量分析

等效锥度太小可能影响车体晃车及蛇行失稳，等效锥度过大将会引起抖车及横向振动报警[7]，严重影响机车运行安全，造成轮轨间不均匀磨耗，因此研究10万km车轮型面匹配变化规律具有十分重要意义。

图9(a)、图9(c)、图9(e)为1～3位轮对不同磨耗型面下等效锥度随横移量变化。初始型面等效锥度，在5 mm横移量以内呈现平缓变化；里程0～2万km，等效锥度曲线变化最明显，1、3位轮对等效锥度变化呈正态分析，且在横移量4 mm左右取得最大值，2位轮对整体低于初始型面呈现平缓变化；随着运行里程的增加，8～10万km下等效锥度曲线变化大致相同。车轮磨耗在前期会导致轮轨匹配急剧变化，随后随着车轮磨耗，会使型面得到优化，轮轨匹配关系达到稳定。图9(b)、图9(d)、图9(f)为1～3轮对名义等效锥度(横移量3 mm)、踏面及轮缘磨耗量(从轮缘顶点向下20 mm横向位移[10])随运行里程变化规律。名义等效锥度在前期变化明显，后期呈稳定变化，1位轮对向初始等效锥度靠近，2、3位轮对远离等效锥度，其中1位轮对磨耗最为严重，轮缘磨耗量达到3.651 mm。轮缘磨耗情况最为严重，后期轮轨匹配关系向初始靠近，轮缘磨耗情况越小，匹配关系较差。

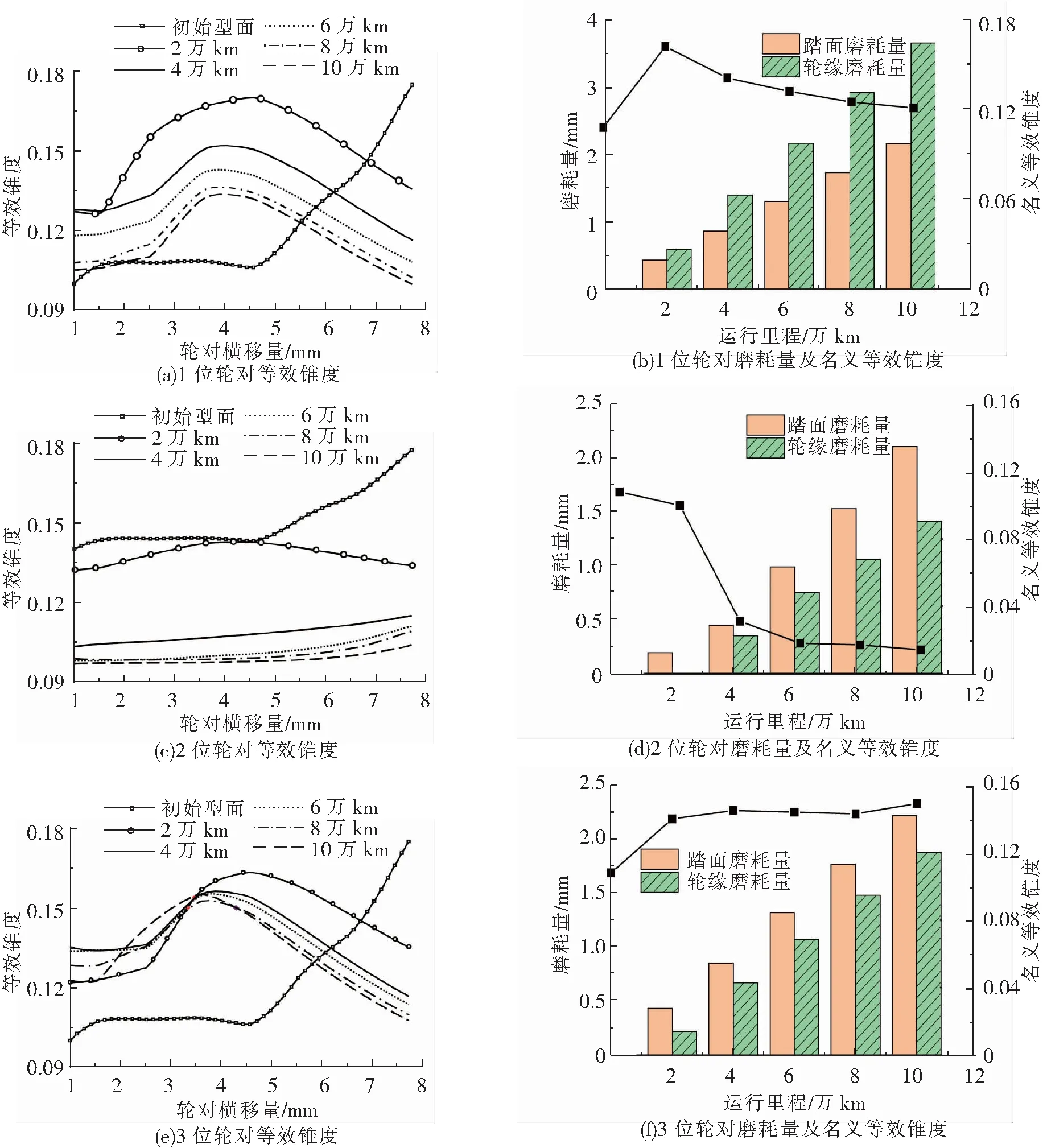
图9 不同运行里程下等效锥度变化

2.3 轮轨接触点分析

表2为10万km下1～3轮对接触点分布情况。初始型面与钢轨接触时，车轮根部靠近轮缘侧分布稀疏，名义等效锥度约为0.108；1～3位轮对运行到2万km，轮对接触线在轨顶上侧分布集中，且车轮根部位置有少量接触线，是明显2点接触，可能造成接触点跳跃现象；随着行驶距离增加，轮缘接触线开始消失，轮轨接触线整体在车轮中部分布，10万km下，2位轮对接触点最宽，名义等效锥度约为0.014。磨耗前期容易造成2点接触，车轮根部有轮缘接触线，其中2位轮对在8万km，轮缘处还有1条接触线，说明存在轮缘与钢轨接触，轮缘磨耗速率较低。对比可知，1位轮对轮缘磨耗速率高，车轮轮缘磨耗严重。

表2 1～3左轮轮轨接触点变化情况

3 结论

(1)对比踏面、轮缘最大磨耗量，仿真与实测结果贴近，进一步验证平均磨耗速率，相差最大为0.063 mm/万km，误差较小；踏面仿真磨耗规律，1位轮对磨耗最严重，2位轮对最小，与实测结果相同。

(2)轮轨接触关系在0～2万km变化明显，8～10万km变化稳定；预测10万km 1～3轮对车轮型面踏面磨耗相差不大，轮缘磨耗最大为1位轮对3.651 mm、最小2位轮对为1.416 mm；轮缘与踏面磨耗达到一定速率，会优化磨耗型面匹配关系，但轮缘磨耗量达不到踏面磨耗速度，会导致车轮型面匹配关系变差。

(3)综上所述，建议0～2万km要对车轮型面进行检查，10万km后对中间车轮进行轮缘镟修。