混凝土空心墩壁厚对日照温差分布的影响分析
2021-12-07胡安庆任东华
胡安庆,任东华
(中铁西南科学研究院有限公司,四川 成都 610031)
由于混凝土导热系数较小,在太阳辐射作用下,混凝土结构内部的温度变化明显滞后于表面的温度变化,形成较大的温度梯度[1-2],而温度梯度引起的温度应力是混凝土裂缝或失效的主要原因[3]。因此,在对空心高墩大跨度桥梁进行设计时,温度作用效应已成为控制因素之一,由于受山体及桥梁上部结构遮荫等因素的影响桥墩的温差效应更难分析。《公路桥涵设计通用规范》[4](简称《公路桥规》)和《铁路桥涵混凝土结构设计规范》[5](简称《铁路桥规》)均对箱梁的梯度温度作用做了相关规定,分别采用折线和幂指数表示温度梯度分布,但关于桥梁日照温差荷载计算,《公路桥规》和《铁路桥规》只局限于箱梁,对桥墩结构没有相应的规定。在桥墩结构的日温差荷载验算过程中,直接采用规范中的日温差作用仍有待商榷。
根据天文学理论光线追踪方法构建了高墩日照分析模型,在模型中考虑了太阳辐射、桥址环境和上部结构遮荫等主要因素,并在宜万铁路马水河桥进行了测试验证分析。根据铁路桥梁空心桥墩壁厚较大的特点,进一步研究了混凝土空心墩壁厚对日照温差分布的影响,为同类桥梁空心墩的日照温差荷载计算分析提供参考。
1 桥墩温度场计算
1.1 桥墩温度场影响因素
结构的温度效应存在太阳辐射的局部性和混凝土结构热传导的不均匀性,一般很难直接根据函数关系求解,只能近似数值模拟求解。桥梁结构受日照作用产生的温度场实质上是一个三维非稳态温度场问题[6]。一般简化考虑可忽略构件纵向的温度梯度,按平面问题计算,再加上合理的边界条件和初始条件,就可以运用差分法进行求解[6]。
第3类边界条件[7]:
(1)
式中,αs为辐射热吸收系数;It为混凝土表面所接受的太阳辐射强度;β为总热交换系数,为对流热交换系数与辐射热交换系数之和;Tw为空气气温;T为墩外壁温度;χ为边界外法线方向。
由式(1)可知,桥墩混凝土表面温度的直接影响因素是日照、气温和热交换。气温测试相对简单,易收集,混凝土表面热交换情况与混凝土材料及空气流动情况相关,可以根据理论经验进行分析;日照受地理位置、季节、周围山体和上部结构对桥墩的遮荫等因素影响较大,最为复杂,需要解决桥墩能否接受到日照和太阳辐射的强度值2个问题。为此,需要了解太阳与地球的相对位置关系,进而研究高墩表面的日照问题。
1.2 太阳光线追踪
太阳与地球的相对位置关系由太阳赤纬δ和时角ω来确定。太阳赤纬确定了地球绕太阳公转的相对位置,时角确定了地球自转的位置关系[8]。
(2)
式中,δ为太阳赤纬;n为年序日。
ω=15(t-12)0≤t<24
(3)
式中,ω为时角;t为真太阳时。太阳高度角是太阳入射光线与地平面的夹角。在地平坐标系中,太阳高度角h的计算式为
sinh=sinφsinδ+cosφcosδcost90°≥h≥0°
(4)
太阳方位角γ的计算式为
(5)
1.3 太阳辐射强度
太阳辐射采用美国供暖、制冷和空气调节工程师协会推荐使用的ASHRAE晴空模型[9]。在山区桥梁计算分析中需要研究桥墩温度场的连续变化过程,所以选用的计算系数是根据我国太阳辐射强度拟合得到的随年序日连续变化的系数。
根据ASHRAE 晴空模型,建筑物接收的太阳辐射由直射辐射、天空散射辐射和反射辐射组成。晴天地球表面的太阳辐射强度值[9]
(6)
式中,IND为垂直入射直射太阳辐射强度;A为大气质量为零时的太阳辐射强度;B为大气的消光系数;h为太阳高度角;CN为大气清洁度。
入射到非垂直表面的太阳总辐射为[6]
It=[max(cosφ,0)+CFws(sinh+C)]IND
(7)
对于垂直表面,ASHRAE晴空模型考虑了太阳周围比较明亮的天空区域,计算公式为[9]
(8)
式中,φ为入射角,即太阳光线与平面法线间的夹角;C为水平面上散射辐射与垂直入射直射辐射的比值;Fws是表面与天空之间的角系数;ρg为地面或水平面的反射率;It为总辐射强度;系数A、B和C的取值可参考文献[8]计算。
虽然计算太阳直接辐射有较好的理论基础,但太阳辐射受云量、空气污染等因素的影响,该计算方法的近似程度较大。对于重要的大型结构物,最好的方法是进行气象观测,实测太阳辐射强度值,但该项工作投入较大,且时间较长,可以到就近的气象台站获取。
1.4 遮荫分析
遮荫可降低高墩的温差荷载,对于高墩桥梁多是建造在深山峡谷中,需要考虑环境对高墩日照的遮挡情况。高墩的遮荫效果有2方面因素,一个是周围山体,另一个是上部结构。
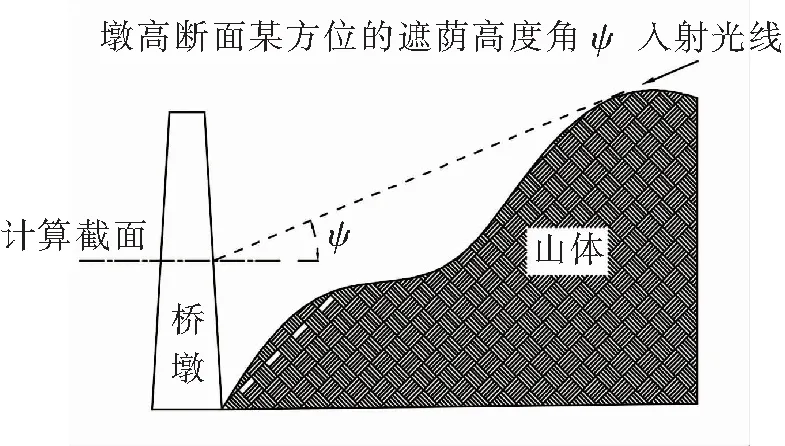
图1 山体遮荫示意图
(2)上部结构遮荫。对于矩形墩顺桥向桥墩外表面,上部结构桥面的阴影边是水平的,但是墩横桥向表面,阴影边是倾斜的。简化考虑,可用该面中心线的荫蔽情况代替该面的荫蔽情况,见图2。

图2 上部结构遮荫计算图示
矩形墩顺桥向桥墩外表面阴影长度
(9)
矩形墩横桥向桥墩外表面阴影长度
(10)
式中,L为顺桥向桥墩外表面到桥面外缘的距离;D为横桥向桥墩中心线到桥面外缘的距离。则桥墩竖直面接受日照必须满足条件:Lz 利用上述算法构建日照模型,分析典型日桥墩太阳辐射情况及外表面温度变化情况,并将边界条件输入至有限元模型,可得到桥墩温度场,基本流程见图3。在实际工程应用上该模型计算量较大,可以编制专用软件程序,利用计算机快速得到计算结果。 图3 桥墩温度场计算流程 宜万铁路高墩桥梁众多,其中马水河桥为该线跨度最大、墩高最高的一座双线预应力混凝土T形刚构桥,位于湖北省恩施自治州建始县,跨度为116 m+116 m,墩高108 m,矩形空心截面,壁厚2~4 m,桥墩壁面编号1~4号,见图4。 之前,厂团委在调研过程中了解到,宋凯在新岗位上遇到一些难题:身为一名主操,他在思考问题时,不能够全方面地分析,自然也就无法做出准确的判断。而和他同在一个单位的马存功也曾经有过同样的困惑。 图4 马水河桥走向 主要计算参数取值为:纬度30.5°,经度109.7°,桥梁为东西走向东偏北7°,当地的大气清洁度根据桥址当地实际情况估算取为0.9,混凝土吸收率和导热系数λ根据试验取0.65、2.32 W/(m·K),采用常风速1 m/s计算总热交换系数[7]。 为了得出该桥梁的典型日照下温度作用,即可能发生的最不利日照温度场分布,在取得环境地形资料的基础上,还就近到建始县气象站查阅了当地30 a(1990年—2020年)的气象资料,重点收集气温、日较差和日照辐射值,并在现场观测高墩的遮荫和温度情况,见图5(以下均为该截面分析结果),以关键部位的温度测点进行验证。通过日照模型,可以得到桥墩全年的理论日照情况,分析出桥墩各个壁面最不利温差出现日期,但是由于天气的不确定性,控制日期并不一定会出现最不利温差,而是在控制日期前后1、2个月都有可能真实出现最不利温差情况,称为典型气象日(典型日)。典型日具有日辐射总量大、气温日较差大、风速小的特征。据收集到的气象资料得知:1993年1月31日,当日最高气温18.0 ℃,最低气温-1.8 ℃,日较差19.8 ℃,且为晴天,日照8.1 h,选为冬季典型日;2019年6月30日,当日最高气温32.1 ℃,最低气温22.0 ℃,日较差10.1 ℃,且为晴天,日照10 h,选为夏季典型日。 图5 桥墩温度测点(95 m高截面) 2.2.1 日照强度理论与实际比较 将冬季和夏季典型日的太阳辐射值(垂直辐射)与模型计算结果比较,见图6。对比发现理论模拟得到晴天的日照强度,在晴朗日期与气象站实测的辐射强度值具有相似的趋势,但由于受大气透明度、云量等因素影响,实测结果一般小于理论结果。 图6 太阳垂直辐射强度理论值与实测值 根据转换理论将垂直辐射强度分解到桥墩4个壁面上,各壁面辐射情况见图7。太阳东升西落,早上、中午和下午分别照射2、4、3号壁面,桥墩1号壁面朝北面不受日照,理论计算结果与实际吻合,并且根据建立的桥墩日照模型得到了桥墩遮荫情况,现场测量遮荫效果与理论模型计算也相符,见图8。 图7 各壁面辐射强度(夏季典型日) 图8 山体遮荫情况(夏季典型日10:00) 2.2.2 夏季典型日桥墩温度 在夏季典型日,考虑遮荫,根据收集到的夏季典型日气象资料,理论推算计算出桥墩外壁的温度演变情况,与实测值基本一致,见图9、图10。 图9 1号壁面温度变化图(夏季典型日) 图10 4号壁面温度变化图(夏季典型日) 2.2.3 冬季典型日桥墩温度 由于现场时间有限,并未能在冬季典型日采集到桥墩温度数据,但是可以根据日照及气温等边界条件,利用Ansys软件可以计算桥梁的温度场[10]。将Ansys软件和自编软件两者计算结果进行比较。 2种计算方法计算冬季典型日墩身4个外壁面温度24 h的变化情况,见图11、图12,均得到13:00时在墩身4号壁板上出现最高温度,此时混凝土内外温差最大。进一步查看该时刻温度沿壁厚的分布情况(图13),可得2种方法计算出的温度分布曲线也十分接近。 图11 桥墩壁面的温度-时间变化曲线(自编软件) 图12 桥墩壁面的温度-时间变化曲线(Ansys软件) 图13 4号壁面温度分布(冬季典型日最大温差) 通过夏季典型日期的日照遮荫情况对比和现场温度测试,冬季典型日理论计算结果与Ansys软件计算结果比较,表明采用构造的桥墩日照模型来分析桥墩的温度场是正确有效的。 为了解不同壁厚桥墩在温差分布上的差异,进行拓展研究。具体分析方法是:仍然采用冬季典型日的温度和日照外界条件[11],采用不同壁厚(壁厚由20 cm至200 cm逐渐增厚)的桥墩模型进行计算分析。研究发现由于桥墩壁厚不同,3号壁板上的最大温差值和最大温差出现时间均有所不同,不同壁厚下的分析结果见图14、图15。 图14 壁厚与最大温差值的关系 图15 壁厚与最大温差出现时间 将计算结果按《铁路桥规》的曲线分别对不同壁厚的最大温差分布进行拟合,结果见表1。 表1 不同壁厚的最大温差、出现时间和分布 由图14、图15和表1可以看出,最大温差随壁厚的增加而增大,其出现时间也随壁厚的增加而延后,且均在壁厚大于80 cm后趋于稳定,温差分布曲线拟合值a的绝对值随壁厚增加逐渐变小,说明温差分布曲线逐渐趋于缓和。 混凝土导热系数小,热传递滞后,且日照时长有限。当厚壁墩(壁厚>80 cm)混凝土表面温度达到最高时,混凝土内部温度仍然没有变化,此时混凝土内外温差最大。然而对于薄壁墩(壁厚<30 cm)的情况却不同,薄壁墩面在受太阳辐射时热量能传入混凝土内部,内部温度也随外温的升高而升高,当混凝土表面温度达到最高时刻内外温差却不是最大,因此不同壁厚最大温差的出现时间也不同。壁厚30~80 cm混凝土的最大温差和出现最大温差的时间都随壁厚的变化而变化,温差分布曲线也随之变化。 根据得出的规律,考虑日照温差的因素,可以将混凝土壁厚进行简单的划分,见表2。 表2 桥墩壁厚的划分 由以上分析可知,壁厚对空心墩的温差分布有较大影响,不同壁厚温差的分布模式不是单一的。根据表1的拟合结果,可知30 cm的薄壁板温差分布拟合得出a的值为7.8,这与《铁路桥规》中的箱梁日温差分布吻合。由此可见,《铁路桥规》只局限于壁厚不大的箱梁,并未充分考虑厚壁对温差分布的影响。 桥梁的温度及其效应对桥梁结构的影响不容忽视,在大跨度桥梁的建设中,设计、施工控制需要做到精细化,桥梁的温度效应分析必不可少。采用“光线追踪算法”建立了高墩太阳辐射分析模型,研究了混凝土空心墩壁厚对日照温差分布的影响,得出以下结论: (1)壁厚对空心墩的温差分布有较大影响,温差的分布模式不是单一的。 (2)混凝土中厚壁墩(30~80 cm),日照温差随壁厚的增加而增加;混凝土厚壁墩(>80 cm)桥墩日照温差不随厚度增加而变化,内部混凝土温度基本不受单日日照的影响。 (3)空心墩的日温差荷载验算,对于混凝土薄壁墩(≤30 cm)直接按《铁路桥规》箱梁日温差荷载取值是合适的,但对于中、厚壁(>30 cm)不宜直接采用。1.5 桥墩温度场计算程序
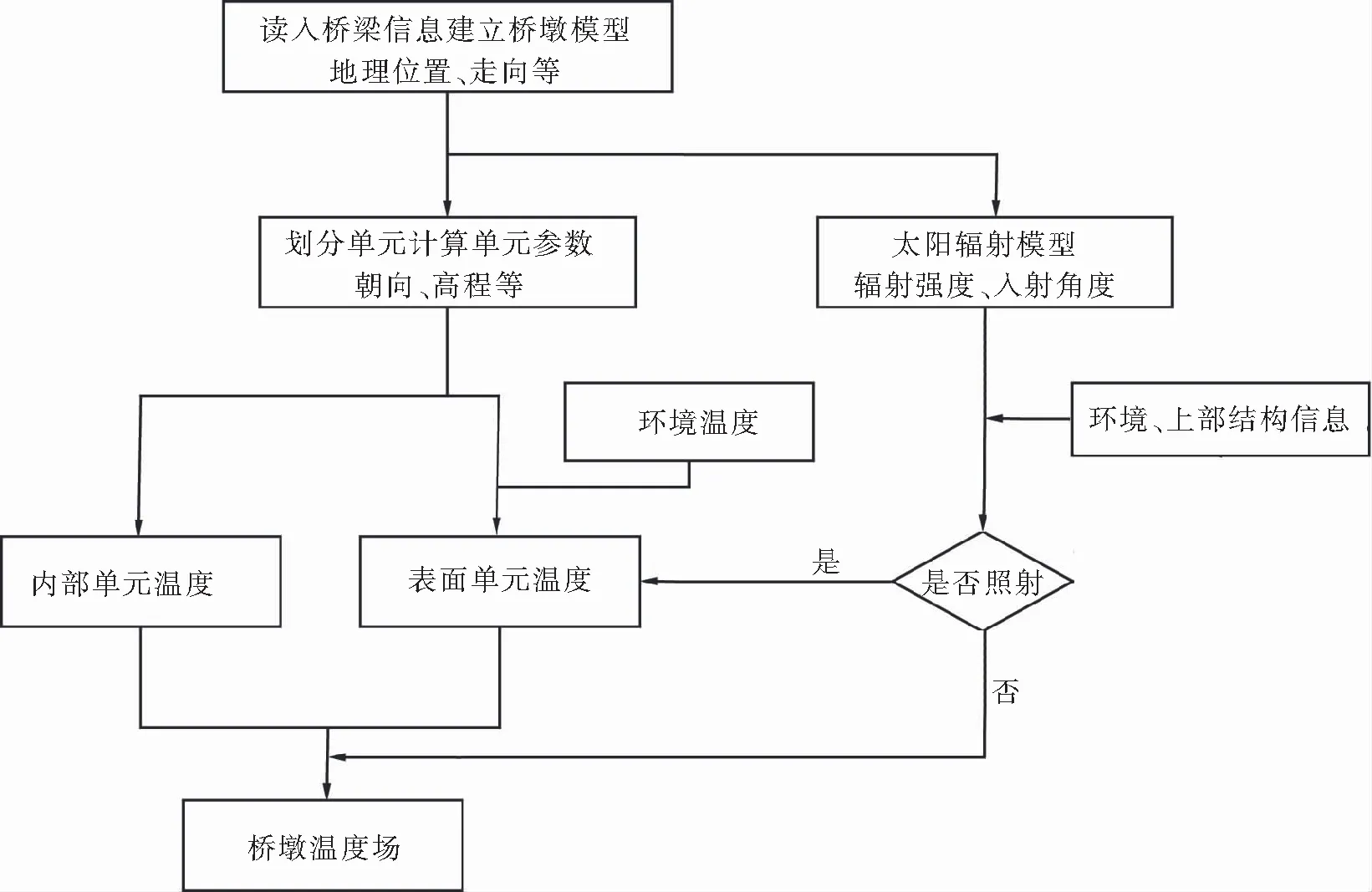
2 工程算例
2.1 桥梁概况
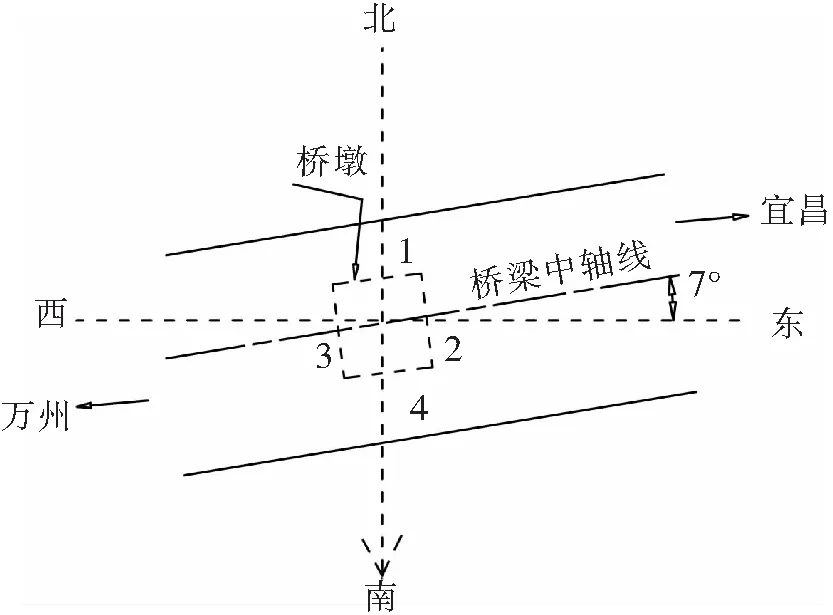

2.2 理论模型验证





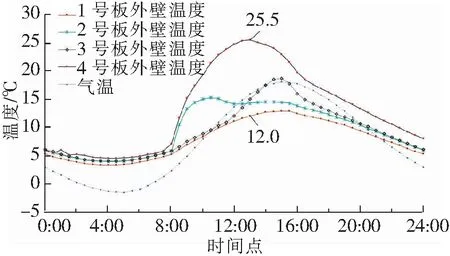

3 空心墩壁厚对温差分布的影响分析




4 结语
