南北向街谷内热不稳定流场日变化规律的模拟研究

张云伟，许 雯，王晴茹，苏军伟，黄 宇，顾兆林

1.西安交通大学 地球环境科学系，西安 710049

2.中国科学院地球环境研究所 黄土与第四纪地质国家重点实验室，西安 710061

近三十年来，我国的城市化发展十分迅速，截至2016年底，我国城镇化率已达到57.35%，比2000年提高了21.15%（国家统计局，2016）。然而，一系列城市环境问题开始凸显，如城市热岛效应、空气污染严重等，已经严重阻碍了城市经济及社会发展（Shao et al，2006），并影响了城市居民的身体和心理健康。随着高密度城市建设的快速发展，一系列的城市规划建设问题逐渐出现，如建筑定位、建筑群体组合方式不合理，绿地、水体面积大量减少等。这些问题会使城市原有的自然下垫面改变，同时城市空间布局不合理还会使城市的通风状况不断恶化，以及城市人为热的排放等都会对城市居民的热舒适感造成严重影响（Zhang and Gu，2013）。城市街谷主要由道路和道路两侧建筑物组合而成，与其周围建筑作为城市冠层的基本单元，是城市大气边界层的重要组成部分，具有显著的街谷微气候特征（顾兆林和张云伟，2011，2014）。街谷热环境的形成原因除了气候条件之外，还与街谷形态和下垫面热物性有关，不仅直接决定了人们在户外空间的热舒适性，同时还会影响街谷内的空气流动和污染物扩散规律（赵敬源和刘加平，2007；Gromke and Ruck，2007；Gu and Zhang，2010；陈 凡 涛 等，2016；苏军伟等，2016；Li et al，2017；Huang et al，2019；Dai et al，2020）。城市街谷作为来往车辆尾气的主要排放场地，同时又是居民日常活动场所之一，其内部的空气流动与污染物的扩散与分布规律一直是国内外学者研究的热点问题。

影响街谷内热环境的现实因素有街谷高宽比、街谷走向、固体表面反射率、人为热、街谷内绿化植被等（顾兆林和张云伟，2014）。在受热街谷内，空气流动主要受两大因素驱动。一是街谷顶部的背景来流，驱动街谷内产生涡流；另一个就是热浮力流，主要是由于建筑物表面和地面的温度高于周围空气的温度，在壁面附近产生向上的浮力流引起的，而热浮力对街谷内流场的影响较为复杂。

Memon et al（2010）通过CFD模拟研究了街谷在不同壁面受热的情况下，来流风速和街谷形状因子对街谷内空气温度的影响。结果表明：迎风墙受热、地面受热和背风墙受热这三种壁面受热情况都使得街谷内平均空气温度与街谷深度呈正相关，与自由来流风速呈负相关。同时，街谷地面受热和背风墙受热促使街谷内空气环流的强度增加；而迎风墙受热情况下，由于反方向的二次漩涡的产生，使得街谷内空气环流减弱。

Allegrini et al（2013）对四种不同的街谷表面受热情况（即迎风墙受热、地面受热、背风墙受热和三表面均匀加热）进行了模拟，分别比较了四种情况下街谷内的湍动能和风速大小。研究结果指出：在低雷诺数的情况下，街谷内流场强度从大到小依次是地面受热、三表面均匀加热、背风墙受热和迎风墙受热；且相对于其他壁面受热情况，三表面均匀加热情况下，街谷内的湍动能最大，最高湍动能出现在街谷顶部的剪切层内，其次是在迎风墙侧。

Tan and Dong（2015）采用商业软件ANSYS FLUENT模拟研究了街谷在不同壁面受热情况下，街谷内污染物扩散与分布的规律。结果显示：迎风墙受热情况下，污染物主要聚集在迎风墙侧的底部，并随着二次漩涡旋转，该二次旋涡会限制污染物向外扩散；背风墙和地面受热的情况下，街谷内污染物的分布规律基本一致，都是随着主漩涡传输，并且在背风墙侧堆积，并且在此情况下，街谷内漩涡膨胀到街谷顶部，有利于污染物扩散。

已有研究表明街谷内受热及温度分布对街谷内流场和污染物扩散有着显著影响（余庄和张辉，2007；Magnusson et al，2014；Dai et al，2020），但是鲜有针对壁面对流换热与长波辐射对街谷内空气温度及流场影响的对比研究。

实际上，一条街谷在一天中的不同时刻，太阳照射情况不同，壁面受热方式也随之变化，从而导致街谷内流场特征发生变化。相比于分析不同受热方式的影响，对街谷内风场及污染物浓度分布的日变化规律的研究，更有助于制定改善街谷内空气质量、减少行人暴露风险的策略。因此，本文选择一条南北走向的城市街谷为对象，对该街谷内空气流动的日变化过程进行模拟研究，并对比分析对流换热与长波辐射的影响。

1 街谷模型及验证

1.1 街谷内热平衡模型

街谷内空气热平衡主要受壁面对流换热和长波辐射、人为热及太阳短波辐射等因素的影响，其中人为热源强度在不同场所差异较大，暂不考虑。所以，街谷内空气热平衡模式主要受长波辐射和各表面对流换热两个主要因素影响，而短波辐射的影响相对较弱，可忽略（Priyadarsini et al，2008）。因此，街谷内空气的热平衡模式可简化为：

式中：ΔQL为大气净长波辐射，单位为W ；QH为对流换热通量，单位为W；ρ为空气密度，取值1.26 kg · m-3；cp为空气定压比热容，取值1012 J · kg-1· K-1；V为街谷内空气总体积，单位为m3；ΔT为街谷内空气温度变化量，单位为K · s-1。

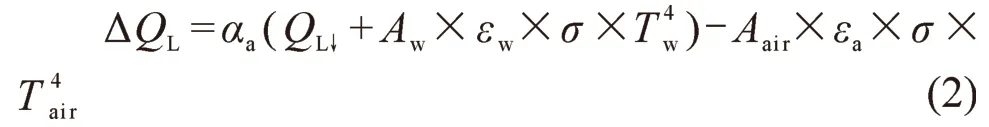
大气在吸收外来长波辐射的同时本身也会向外发射红外长波辐射，有时其放射量甚至会超过其吸收量，因此，必须同时考虑大气长波辐射的吸收和辐射（李万彪，2010），可由式(2)计算：式中：QL↓为大气逆辐射，单位为W；αa为大气长波辐射吸收率；εw为壁面长波辐射率；εa为大气长波辐射率，根据基尔霍夫定律αa=εa；Tw为壁面温度，单位为K；Tair为大气温度，单位为K；Aw、Aair为壁面面积和街谷内空气表面积，单位为m2；σ为斯蒂芬-玻尔兹曼常数，取值5.6696×10-8W · m-2· K-4。

在有限尺寸大小的街谷内，可忽略空气对大气逆辐射的吸收（张宇峰，2016）。

对流换热主要是指在有流体流经表面时所发生的热量传输现象。在裸露街谷内，主要是建筑表面、地面与空气的对流换热（Campbell and Norman，1999）。因此，裸露街谷内：

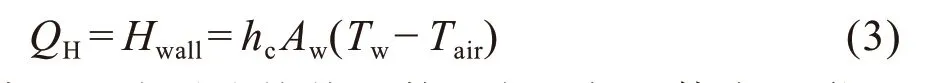
式中：hc为对流换热系数，主要与固体表面附近风速有关，单位为W · m-2· K-1。

1.2 控制方程及求解

本文湍流模拟采用大涡模拟方法，亚格子模式选用Smagorinsky（1963）模式，Navier-Stokes方程经过滤波后可表示为：

式中：i，j为张量指标，取值为1，2，3，分别对应空间的x，y，z方向；u1，u2，u3分别表示速度的3个分量 ——u，v，w，单位为m · s-1；t为时间，单位为s；P为大气压强，单位为Pa；Si、ST分别是动量方程和能量方程的源项；υ和υSGS分别是空气粘性和亚格子粘性，单位为m2· s-1；Pr、PrSGS分别是Prandtl数和亚格子Prandtl数，分别取0.72和 0.33（Uehara et al，2000）；δi3为Kronecker函数。

本文数值模拟采用OpenFOAM软件包实现，基于有限容积方法对控制方程进行离散，并采用PIMPLE算法处理速度和压力的耦合问题。

1.3 模型验证

本文通过与Uehara et al（2000）的风洞试验结果对比来验证数值模拟方法的准确性。街谷模型的横截面示意图如图1所示。街谷尺寸大小是0.1 m×0.1 m×0.2 m，分别对应流向（x方向）、垂直方向（y方向）和展向（z方向），街谷形状因子为1。地面温度Tg为352 K，其他壁面温度为293 K，来流空气温度Tin为293 K，壁面长波辐射系数取0.9，建筑物上方区域来流初始风速分布呈指数分布，由下式计算：

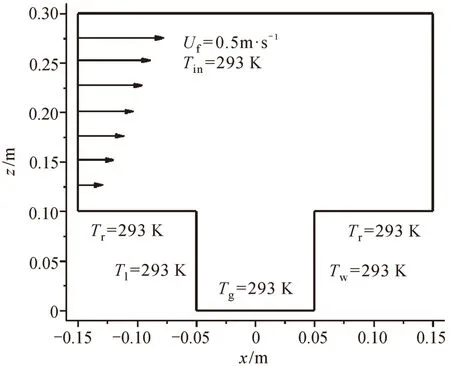
图1 街谷模型的横截面示意图Fig. 1 Sketch map on the cross section of the street canyon model

式中：Uf为建筑物顶部来流参考风速，本文取值0.5 m · s-1；H为街谷高度，本文取值0.1 m；b为街谷顶部到计算区域顶部的距离，本文b= 2H。

流向和展向方向上为循环边界条件，顶部采用滑移边界条件，建筑物表面为壁面边界条件。街谷内网格分辨率Nx×Nz×Ny为20×20×40，在壁面附近和建筑顶部高度进行网格加密，近壁面最小网格为0.003 m，离壁面较远的区域采用粗网格，网格渐变比例约1.1，其中Nx、Nz、Ny分别代表街谷内计算区域在x、z、y三个方向上的网格数。模拟条件与Uehara实验中Rb= - 0.21的案例所对应条件一致。

图2所示为街谷中心垂直线上（x= 0）无量纲流向速度与温度的统计平均结果比较。其中，算例“present simulation”中只考虑壁面对流换热；而算例“present simulation ＋ radiation”既考虑了壁面对流换热又考虑了壁面长波辐射，以分析壁面长波辐射对街谷内流场和温度场的影响。总体上，本文数值模拟结果与风洞试验数据吻合得较好，变化趋势完全一致。其中，街谷顶部的速度变化率比风洞实验结果要小，而温度变化在0.1H高度附近与实验结果差别较大。

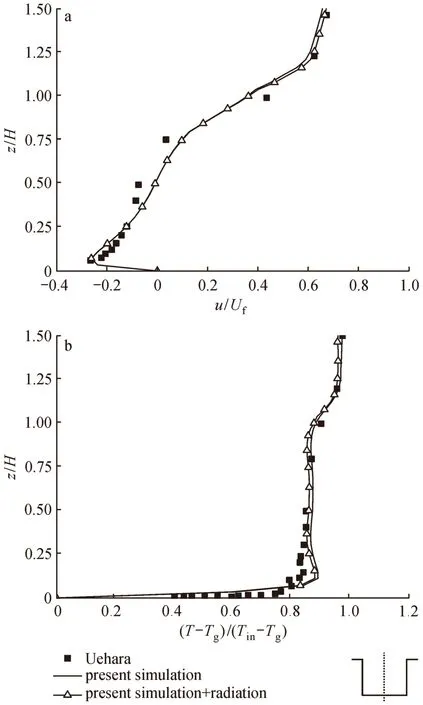
图2 街谷中心垂直线上（x= 0）流向速度（a）与温度（b）的比较Fig. 2 Comparison of the streamwise velocity (a) and temperature (b) on the central vertical line (x= 0) of the street canyon

表1给出了两个数值模拟算例的结果与Uehara风洞实验结果的误差分析。速度和温度的误差都在5%以内，而考虑了壁面长波辐射以后，偏差值变化也不到0.5%。可见，表面辐射虽然能增加街谷内温度，但对街谷内温度场和流场的影响很小。

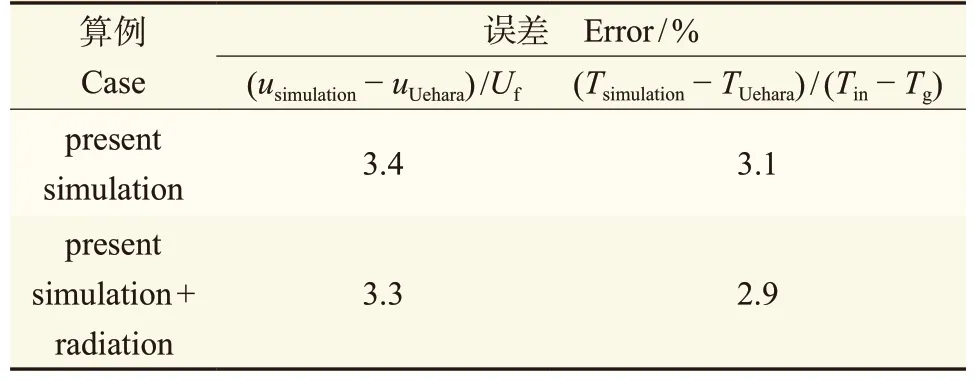
表1 模拟结果与实验数据的误差Tab. 1 Error analysis between simulated and measured data

图3分别展示了街谷中心垂直线上（x= 0）流向速度脉动量根均方值urms垂直方向速度脉动量根均方值wrms的分布。总体上，本文模拟结果与Uehara et al（2000）风洞实验结果变化趋势一致，脉动量根均方最大值主要分布在街谷顶部和地面附近区域；但是本文模拟结果在数值上比Uehara et al（2000）风洞实验结果略小，原因可能是在模拟过程中每个节点上样本数据的采集频率较风洞试验的偏高，造成模拟试验的数据样本量较多，从而使得模拟结果的脉动量变化较为缓和。另外，本文模拟中网格数量相对较少，也会导致湍流模拟精度偏低。

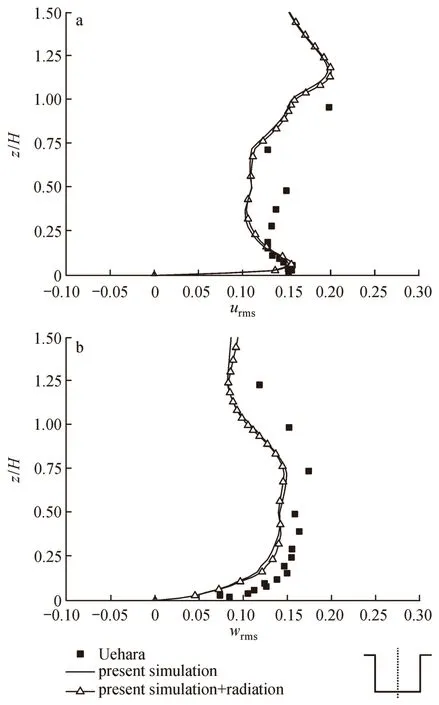
图3 街谷中心垂直线上（x= 0）流向（a）和展向（b）脉动量根均方值比较Fig. 3 Comparison of the streamwise (a) and spanwise (b) root mean square values of velocity on the central vertical line (x= 0) of the street canyon

总体而言，本文所采用的数值模拟方法无论是从定性还是定量上都能够较好地模拟出街谷内热不稳定流场及湍流特征。同时关于壁面长波辐射对街谷热环境的影响分析结果显示，作为情景模拟，街谷内的温度分布以及流场分布特征主要是受壁面对流换热的影响，受壁面长波辐射影响不大。

2 街谷内流场日变化模拟

2.1 街谷模型与算例安排

为了更接近实际情况，本文以西安市和平路街谷为样本（Zhang et al，2012；张云伟等，2016），构建一个街道宽20 m，建筑高20 m，展向（y方向）取40 m，形状因子为1的理想街谷模型；街谷内网格数Nx×Nz×Ny为30×30×40，在壁面附近和建筑高度采用细网格，离壁面较远的区域采用粗网格，靠近壁面的最小网格尺寸为0.16 m，计算区域顶部网格最大为2.5 m；街道是南北走向，来流为东风，水平方向风速u在建筑物上方区域为指数分布，由公式(7)计算，其中Uf取值2 m · s-1；H为街谷高度，取值20 m，则b取定值40 m；垂直方向速度w和展向速度v的初始值都是0；来流和固体壁面的温度根据夏季在和平路街谷内现场测量的结果确定（Zhang et al，2012），不同时刻温度设置条件如图4所示。流向和展向分别采用循环边界条件；顶部为滑移边界条件，街谷各固体表面为无滑移壁面边界条件。需要说明的是，在进行实际尺寸街谷内风环境模拟时，本文所选网格是合适的（顾兆林和张云伟，2014）。

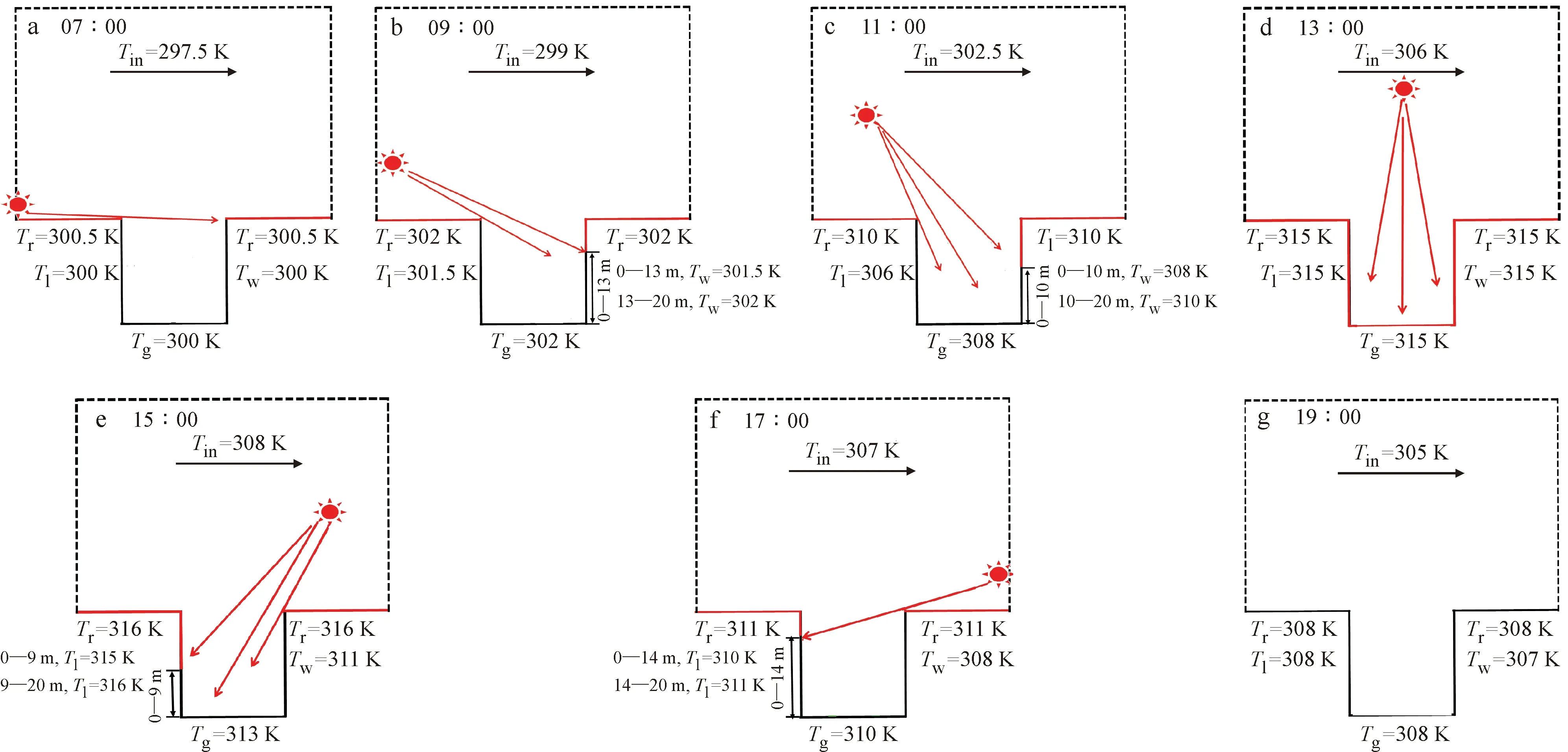
图4 在西安市和平路街谷内测得不同时刻温度分布Fig. 4 Temperature distribution within the street canyon measured on Heping Road street canyon in Xi’an at different time

模拟中仍然设计了两组算例，在“case1”组算例中，只考虑壁面对流换热，而在“case2”组算例中，既考虑壁面对流换热，又考虑壁面长波辐射的影响，算例编号如表2所示，末尾的数字代表算例对应的时间，比如case1就包含case1-7至case1-19这7个算例，分别对应不同的时间。模拟时间步长为0.04 s，收敛判据为残差小于10-5，模拟时间为4000 s。

表2 街谷模拟算例编号Tab. 2 Simulation cases and the number

图5给出了算例case1-13和算例case2-13模拟的街谷内平均气温Tm随模拟时间的变化，Tm是每个模拟时间步街谷区域内所有网格上空气温度的平均值。街谷内平均温度在2000 s后基本已经达到稳定，因此以下情景模拟结果的统计平均在2000 — 4000 s时间区间进行。

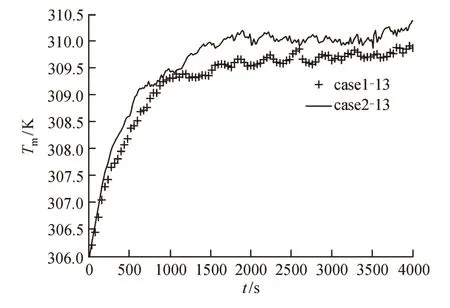
图5 街谷内温度Tm随模拟时间的变化Fig. 5 Change of temperature Tm with simulation time within the street canyon

2.2 街谷内温度场变化

图6和图7分别给出7个时刻街谷展向中截面的两条中心线（x= 0和z= 10 m）上统计平均温度Tmean的变化曲线。本文利用7个不同时刻街谷热环境的模拟结果来反映街谷内热环境的日变化规律。可见，07∶00以后，街谷内空气温度逐渐升高，15∶00达到最大，可达311 K（38℃）；15∶00之后街谷内空气温度逐渐降低，19∶00降到最低值，这与一天中太阳的辐射强度是呈正相关的。两种计算条件下，街谷内温度的分布趋势是一致的，高温区主要出现在街谷顶部和各固体表面附近，街谷内中心位置区域的温度分布较为均匀，壁面长波辐射的引入（case2）使得街谷内空气温度要大于算例case1的模拟结果，但是增加量非常小。

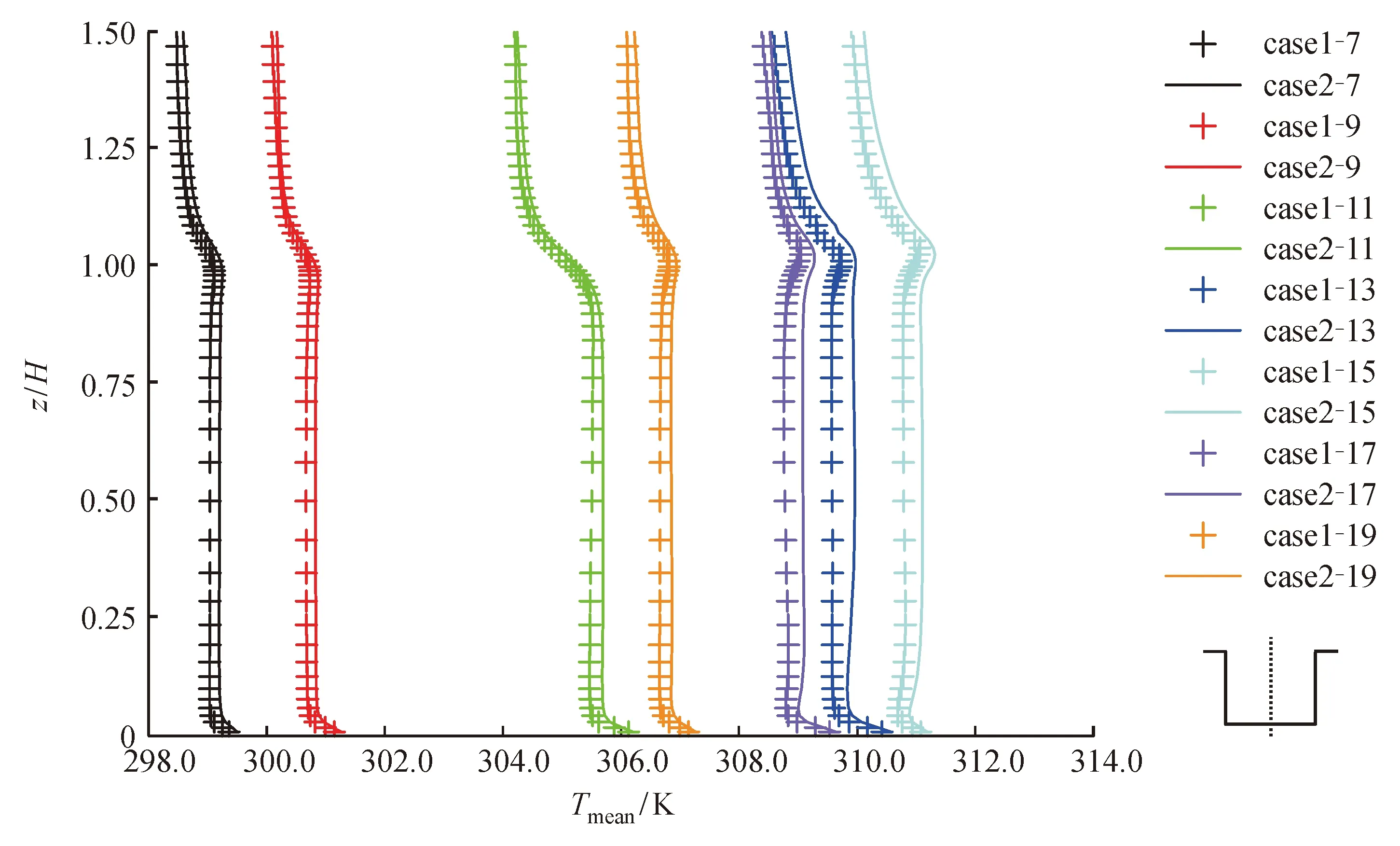
图6 不同时刻街谷展向中截面中心线（x= 0）上统计平均温度Tmean的分布Fig. 6 Distribution of mean temperature Tmean on the centerline (x= 0) of the spanwise middle section in the street canyon at different time

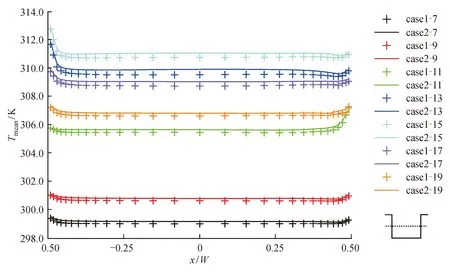
图7 不同时刻街谷展向中截面中心线（z = 10 m）上统计平均温度Tmean的分布Fig. 7 Distribution of mean temperature Tmean on the centerline (z = 10 m) of the spanwise middle section in the street canyon at different time

表3给出了两组算例的空气温度相对增长量ΔT/Tin，其中ΔT表示在街谷内流场达到稳定之后，街谷内统计平均温度Tmean与来流初始温度Tin的差值，即ΔT=Tmean-Tin，代表街谷内平均空气温度的增加量。可以看出，街谷内温度的变化主要是受壁面对流换热的影响，壁面辐射的影响非常小；从早上07∶00到中午13∶00，随着壁面温度的增加，壁面对空气的加热也逐渐增强，13∶00以后壁面加热强度开始减弱；在不考虑长波辐射的情况下，13∶00空气温度的相对增长量为1.22%，街谷内空气温度比来流温度高约3.7 K；同时刻在考虑长波辐射的情况下，空气温度的相对增长量为1.31%，街谷内空气温度比来流温度高约4.0 K。可见，即使在正午长波辐射最强时，长波辐射引起的街谷内空气温度升高值只有0.3 K，也不到对流换热影响的10%。

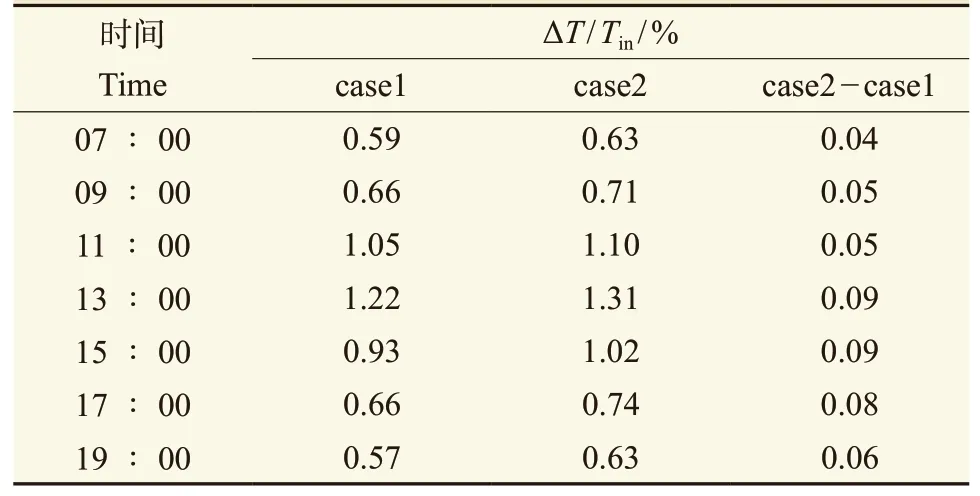
表3 街谷内空气温度相对增长量ΔT / TinTab. 3 Relative change ratio of air temperature ΔT / Tin in street canyon

2.3 街谷内风场变化

图8和图9分别是case1和case2两组算例模拟所得街谷展向中截面的两条中心线（x= 0和z= 10 m）上的统计平均速度u/Uf、w/Uf的分布曲线。结果显示：街谷顶部和各壁面附近风速较大，街谷中心处风速最低。从07∶00到11∶00，街谷内平均风速逐渐减小，到11∶00达到最低值。这主要是因为上午这段时间，随着迎风墙壁面温度逐渐增加，迎风墙侧热浮力与街谷内气流主漩涡方向相反，削弱了街谷内环流强度，甚至在迎风壁面附近形成反向漩涡，造成迎风墙侧垂直方向速度为正值。11∶00至13∶00随着壁面温度与空气温差逐渐增大，流场强度逐渐增大，13∶00街谷内流场强度达到最大值。13∶00之后随着壁面温度逐渐降低，壁面温度与空气温差逐渐减小，街谷内流场强度逐渐降低，在19∶00降到最低。

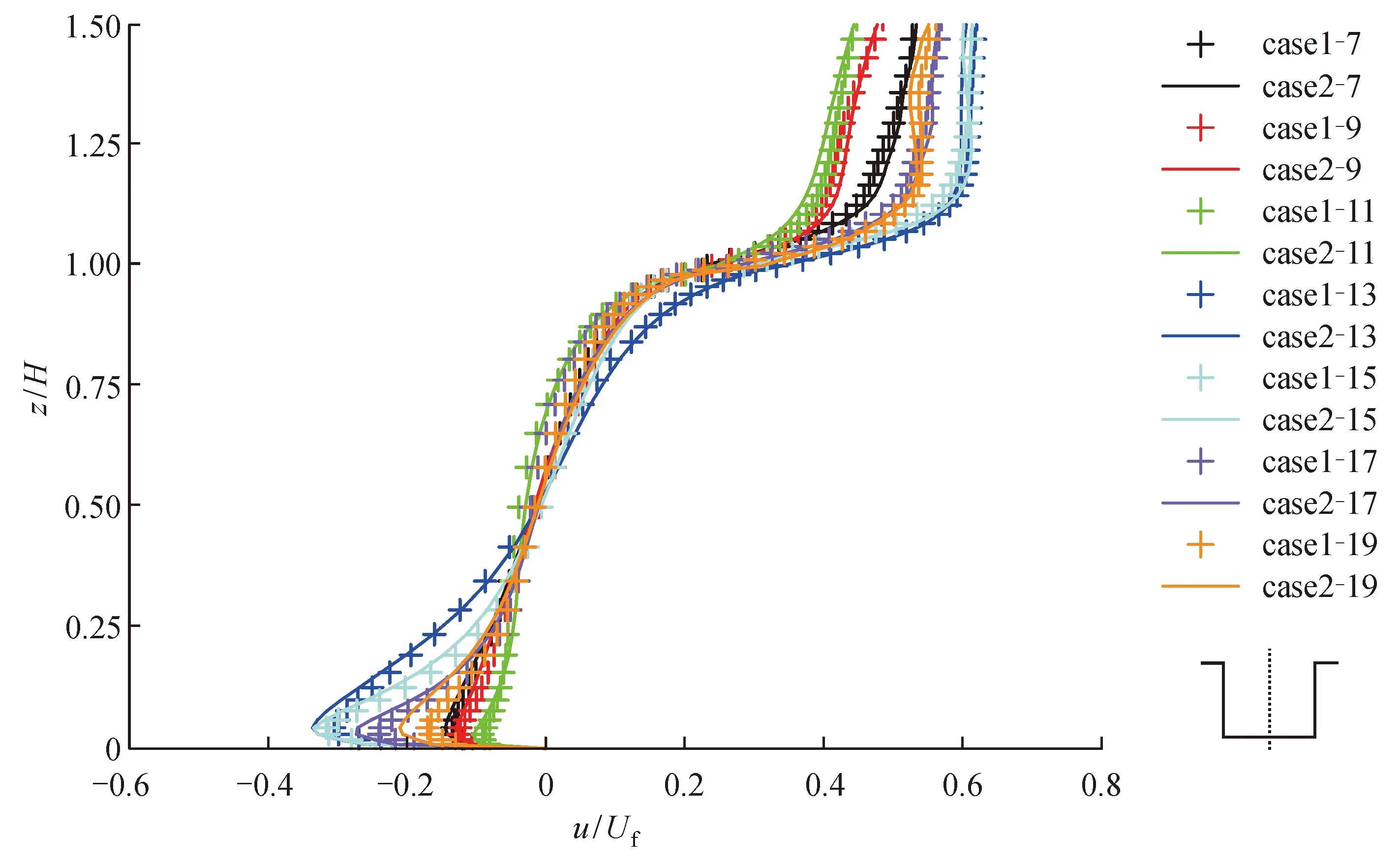
图8 不同时刻街谷展向中截面中心线（x= 0）上的流向速度分布Fig. 8 Distribution of streamwise wind velocity on the centerline (x= 0) of the spanwise middle section in the street

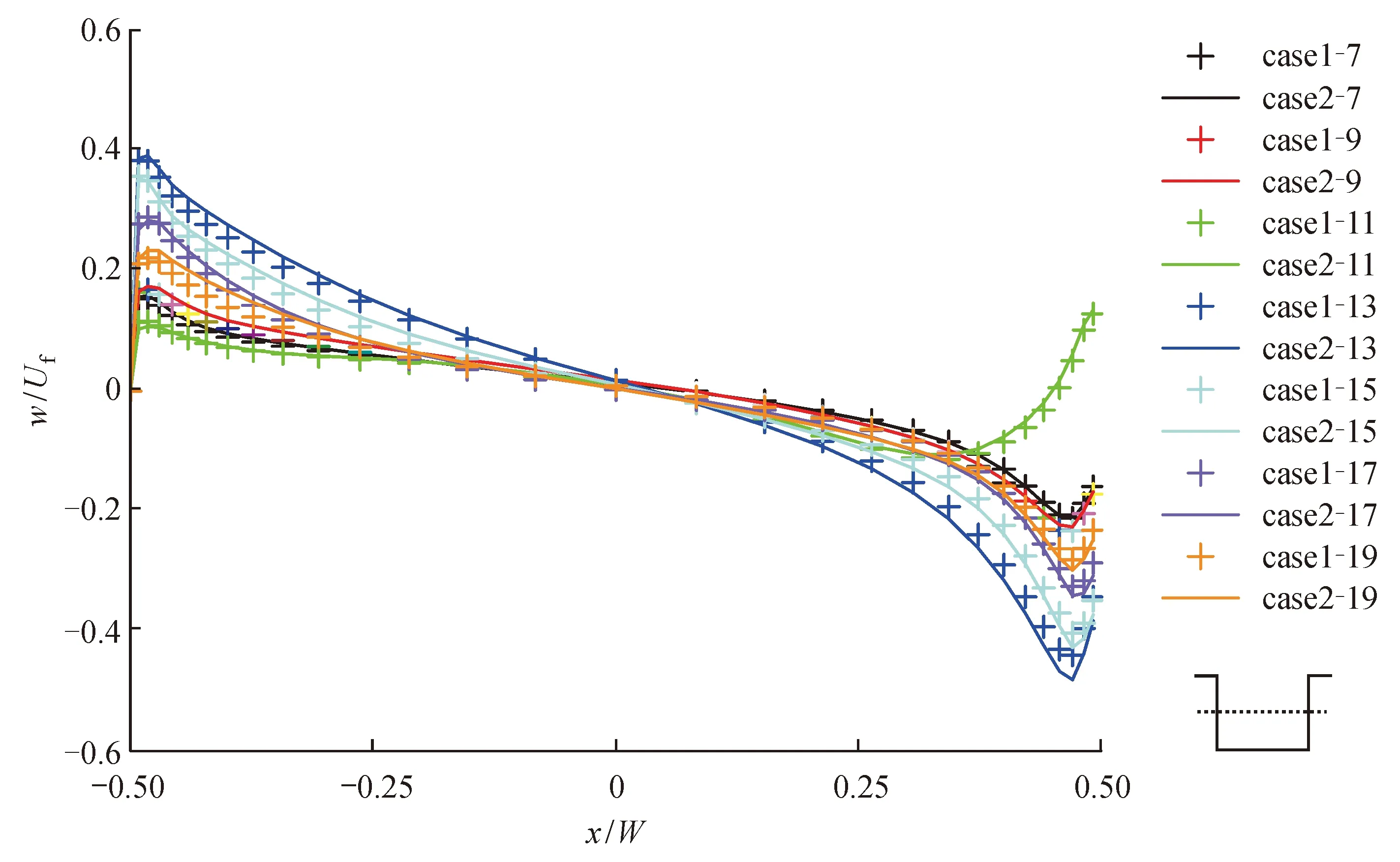
图9 不同时刻街谷展向中截面中心线（z= 10 m）上的垂直方向速度分布Fig. 9 Distribution of vertical wind velocity on the centerline (z= 10 m) of the spanwise middle section in the street canyon at different time

总体而言，下午太阳直照背风面墙壁，背风面墙壁温度较高，背风面墙壁热浮力与街谷内气流主旋涡方向一致，加强了街谷内环流强度，因此13∶00以后，下午时段街谷展向中截面上的风速总体上比上午的风速大，更有利于污染物扩散。

对case1和case2这两组算例的对比分析结果显示，7个时刻街谷内统计平均速度的水平分布和垂直分布趋势都相差非常小，原因主要是在给定环境参数的情景模拟中，壁面辐射对街谷内温度场的影响较小，导致街谷内温度分布变化非常小，所以对街谷内平均流场的影响也较弱。

图10和图11分别是7个时刻case1和case2这两组算例的展向中截面的两条中心线（x= 0和z= 10 m）上的脉动量根均方值urms、wrms的分布。街谷内脉动量根均方值最大值主要分布在街谷顶部和各表面附近，街谷中心处最低；07∶00、09∶00和11∶00，街谷底部和迎风墙侧的脉动量根均方值较大，主要是街谷底部和迎风墙附近向上的浮力流所致；13∶00和15∶00街谷顶部的脉动量根均方值达到最大，在15∶00之后街谷内脉动量根均方值逐渐降低。两组算例case1和case2的脉动量根均方值的水平分布和垂直分布趋势都相差很小。

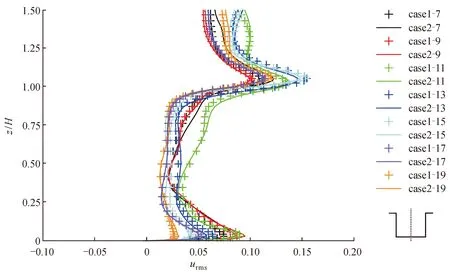
图10 不同时刻街谷展向中截面中心线（x= 0）上流向速度脉动量根均方值分布Fig. 10 Distribution of root mean square of streamwise wind velocity on the centerline (x= 0) of the spanwise middle section in the street canyon at different time

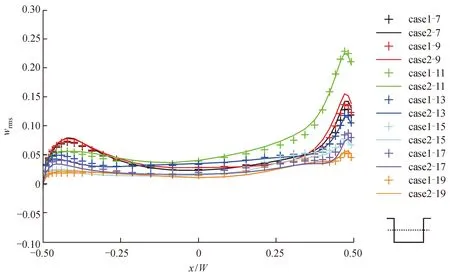
图11 不同时刻街谷展向中截面中心线（z= 10 m）上的垂向速度脉动量根均方值分布Fig. 11 Distribution of root mean square of vertical wind velocity on the centerline (z= 10 m) of the spanwise middle section in the street canyon at different time

其中，从图8 — 11还可以看出算例case1和case2的平均速度和脉动量根均方值在街谷的固体壁面附近略有差异。为进一步定量地分析壁面长波辐射对街谷内流场的影响程度，表4给出了算例case2的速度和脉动量根均方值相对于算例case1的绝对误差。由表4中数据可知壁面辐射对街谷内流场的影响很小，对平均风速的影响小于2%，而对脉动量的影响更是小于1%，可以忽略，这与Priyadarsini et al（2008）得出的结论一致。

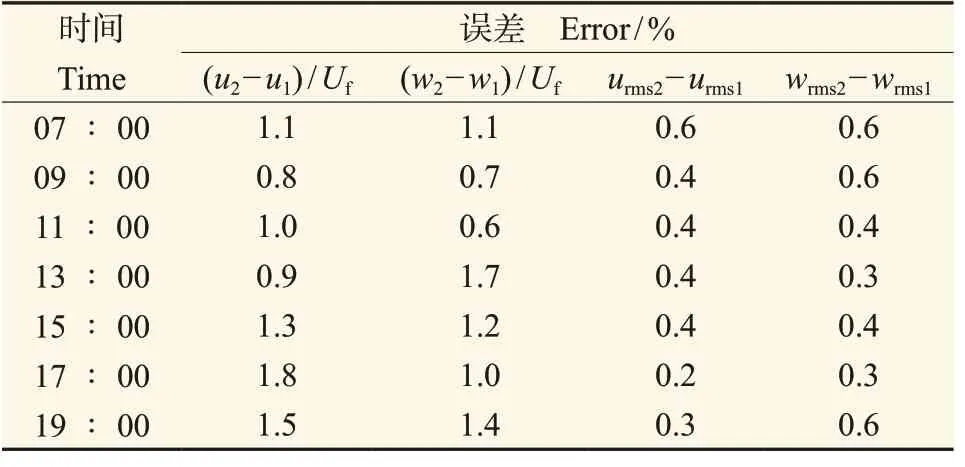
表4 算例case2的速度和脉动量根均方值的误差分析Tab. 4 Error analysis of velocities and root mean square values of case 2

3 结论

本文基于街谷内热平衡分析，结合大涡模拟方法，研究了一个南北走向的城市街谷内温度、风场的日变化特征，并分析了壁面对流换热及长波辐射对街谷内环境的影响。结果显示：街谷内温度和风场主要受壁面对流换热的影响，长波辐射的影响非常小，长波辐射引起街谷内空气温度升高小于对流换热影响的10%，而其对平均风速和脉动量的影响更是在2%和1%以内，可以忽略长波辐射的影响以减少计算量；上午街谷内空气温度呈增加趋势，直到午后气温达到最大；气温高的区域主要出现在街谷顶部和各固体表面附近，街谷内中心区域的空气温度分布较为均匀；街谷内风速变化趋势与气温相反，上午呈减弱趋势，主要是因为上午这段时间，随着迎风墙壁面温度逐渐增加，迎风墙侧热浮力与街谷内气流主漩涡方向相反，削弱了街谷内环流强度；上午时段，街谷底部和迎风墙侧的湍流脉动较强，而下午时段街谷顶部的湍流脉动更为剧烈，直到下午15∶00之后，街谷内湍流呈逐渐下降趋势。

街谷内温度分布、风场及湍流特征都有着规律的时空变化特征。在街谷内的不同壁面和不同时段内，通过建筑材料的选取和建筑表面结构设计，适当调控建筑壁面的温度，可以促进街谷内温度分布、空气流通及污染物扩散效果的改善，该结果可供相关建筑设计参考。