具有价格歧视的多厂商斯塔克博格博弈的均衡分析

罗 萍, 宋奇庆, 张伟莉

(1.桂林理工大学 理学院, 广西 桂林 541006; 2.山西师范大学 数学与计算机科学学院, 山西 临汾 041000；3.东北财经大学 管理科学与工程学院，辽宁 大连 116025)

0 引 言

古诺博弈模型由Cournot在1838年提出, 假设市场上有销售同质产品的寡头, 寡头以产量为策略进行博弈, 获取利润最大化。如今, 古诺博弈模型已成为博弈论的基本模型之一。古诺博弈还依赖于消费者行为、寡头对需求的期望、寡头的数量等, 因此, 古诺博弈得到了广泛持续的关注, 并产生了丰富的研究成果。区别于静态古诺模型[1-3], 还有动态古诺模型[4-5]等。不同于古诺博弈中寡头同时采取行动, 斯塔克博格博弈中寡头采取行动有先后顺序, 近年来得到进一步推广[6]。作为古诺博弈的深入推广, 一般Nash平衡理论及应用得到了持续研究, 这对均衡的理解有进一步启示[7-9]。

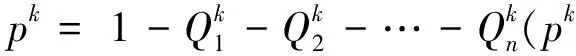
基于当前研究对价格歧视现象的关注, 还未见多厂商斯塔克博格博弈的价格歧视现象报道, 本文探讨了价格歧视对多个对称寡头斯塔克博格竞争的影响, 得到了子博弈完美纳什均衡与厂商数n和目标群体分类数K的关系，对比无价格歧视的情况, 进一步研究表明对有价格歧视的多厂商斯塔克博格博弈, 领头厂商对商品的售卖价格关于群体数增加且边际递减, 领头厂商的最优产量与群体数n以及市场中的厂商数量n无关, 而任一后动厂商的市场平均售价与K无关。

1 有价格歧视的n厂商斯塔克博格博弈与结果

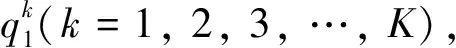
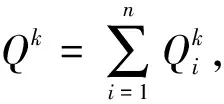
定理1具有价格歧视的n厂商斯塔克博格博弈的唯一子博弈完美纳什均衡为

和

证明：在边际成本相等都为c的情况下, 对Qk利用对称性, 有

(1)

为表达方便, 令α=a-c, 则厂商i的利润可表示为

(2)

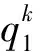
(3)

则

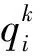
(4)

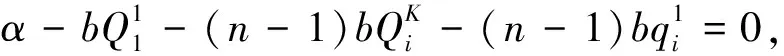
从而有关系式

(5)

再考虑第一阶段, 先动厂商1需最大化其收益π1。由式(1)和式(2)知，

(6)

将式(5)代入式(6)为

将式(4)代入上式, 有

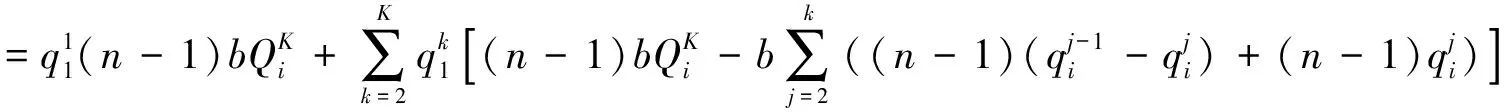
再由式(5)进一步可得

再整理, 结合式(4)有

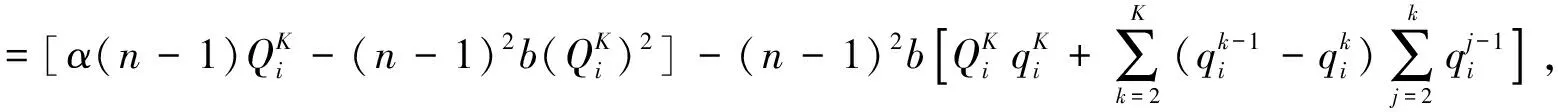
进一步计算得

(7)

(8)

注意到由式(4)可得

(9)

将式(9)代入式(8)有

即

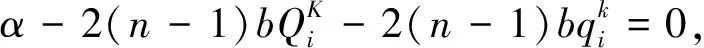
整理得

(10)

把式(10)关于k=1, 2, …,K累加, 有

则

(11)

由式(10)和(11)有

(12)

由式(4)、(12)得

再由式(5)、(11)、(12)可得

证毕。

由定理1可见, 在均衡点处, 领头厂商1获得最大利润, 它只对价格最高的消费群体提供产品。相对于其他n-1个后动厂商, 厂商1的先动优势使得其能对相同的产品售出最高的价格。

对于无价格歧视的n厂商斯塔克博格博弈, 即当K=1时, 由定理1可以推得对应的均衡如下, 其也是文献[22]中的式(8)和(9)。

推论1无价格歧视n厂商斯塔克博格博弈的唯一子博弈完美纳什均衡为

q1=(a-c)/(2b),

和

qi=(a-c)/[4(n-1)b], ∀i=2, 3, …,n。

定理2在有价格歧视的n厂商斯塔克博格博弈中, 均衡点处先动厂商1对商品的单一售价p1为群体数K的增函数且与厂商数n无关, 任一后动厂商i的市场平均售价piav与K和n无关。

证明:由定理1可知,n个厂商对前k个群体的总销量为

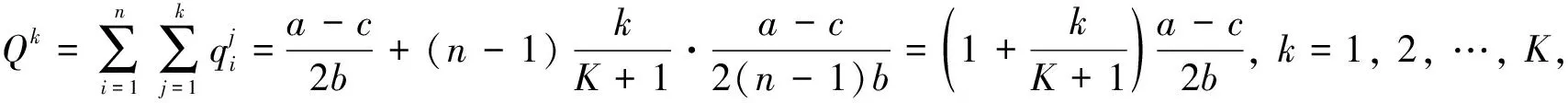
则逆需求价格函数pk为

因此, 领头厂商1唯一的售价为

可以看出p1为K的增函数, 并且与n无关。

后动厂商i(i=2, 3, …,n)销售产品的平均价格piav为

可见,piav与K、n无关。证毕。

2 结果分析与有无价格歧视的比较

当市场无价格歧视时, 由推论1可知: 领头厂商1的最佳产量决策为

q1=(a-c)/(2b)，

后动厂商i的最佳产量决策为

qi=(a-c)/[4(n-1)b],

因而有逆需求价格函数

p=a-b(q1+(n-1)qi)=(a+3c)/4。

即该市场总平均价格为

pav=(a+3c)/4。

可以发现:pav与有价格歧视时后动厂商的平均售价piav一致, 见定理2。

厂商1获得的对应利润为

π1=(a-c)2/(8b),

厂商i所获利润为

πi=(a-c)2/[16b(n-1)], ∀i=2, 3, …,n。

当n=1时, 市场不存在斯塔克博格竞争; 可以看出,n≥2时,π1>πi, ∀i=2, 3, …,n, 即市场上领头厂商1的利润始终大于后动厂商利润, 领头厂商1的利润是后动n-1个厂商利润之和的2倍。在无价格歧视的斯塔克博格竞争中, 可以得出: 当竞争厂商数目n不断增大时, 领头厂商始终具有先动优势, 获得信息多的后动厂商并没有获得更多的利润。

当市场存在价格歧视时, 由定理1知, 领头厂商1对产品的销售价格为

后动厂商i销售产品的平均价格piav为

piav=(a+3c)/4, ∀i=2, 3, …,n,

故而, 市场的总平均价格pav为

领头厂商1的最优利润为

后动厂商i的最优利润为

在有价格歧视的情况下, 随着群体数K的不断增大, 领头厂商1售卖的价格p1不断增大, 而后动厂商i的市场平均价格piav不变; 领头厂商的利润Π1也随着群体数K的不断增大而增大, 而且Π1与厂商数n无关, 即厂商1的利润不会随厂商数目的增多而变少, 后动竞争厂商的利润随着厂商数目n的增多而被摊薄, 但当厂商数n固定时, 后动厂商的利润也会随群体数K的不断增大而增大。当n≥2时,Π1>Πi, 即先动厂商的利润大于后动厂商的利润, 先动厂商利润是后动n-1个厂商利润之和的2倍。

因此, 对于n厂商斯塔克博格竞争, 厂商1先采取策略, 其余n-1个厂商后采取策略, 比较无价格歧视与有价格歧视的情形, 有以下结论:

结论1无价格歧视时的市场总平均售价pav与有价格歧视时后动厂商的平均售价piav一致。

结论2市场引入价格歧视后, 所有厂商的利润增加量随着群体数K的不断增大服从边界递减规律, 先动厂商1利润Π1的上界为(a-c)2/4b; 后动厂商i的利润Πi的上界为(a-c)2/[8(n-1)b]。

结论3无论市场有无价格歧视, 先动厂商的利润是所有后动厂商利润之和的2倍，且先动厂商的利润与厂商数目n无关。

结论4采取价格歧视销售策略时, 所有厂商的利润大于无价格歧视时的利润。

如图1, 可以看出当有价格歧视时(a=1,b=1,c=0.2,n=3), 利润随着K的增大而增大, 逐渐趋于平稳, 对厂商而言, 考虑到群体数增加带来的分类管理的成本的增加; 当K较小时, 价格歧视策略对厂商带来的利润改观最为明显; 增加群体分类数K, 利润的净增加效果服从边际递减规律;Πn总大于πn。

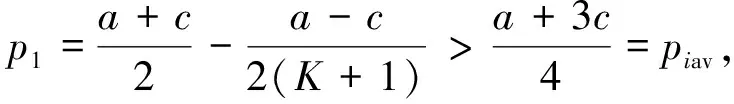
采取价格歧视销售策略时, 先动厂商1销售商品的价格大于后动厂商的价格, 而每一个后动厂商销售商品的平均价格不受影响。如图2所示, 当有价格歧视时(a=1,b=1,c=0.2,n=3), 后动厂商销售商品的平均价格并未改变, 先动厂商1销售商品的价格如图1中的利润一样随着K的增大而增大, 服从边际递减规律; 当K较小时, 价格歧视策略对先动厂商1销售价格改变的影响最为明显。

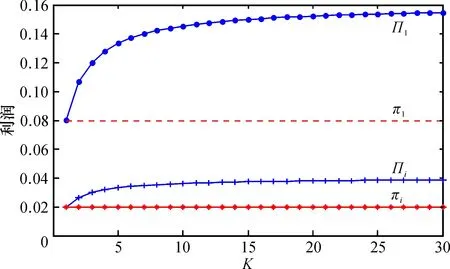
图1 厂商利润在有无价格歧视时的对比

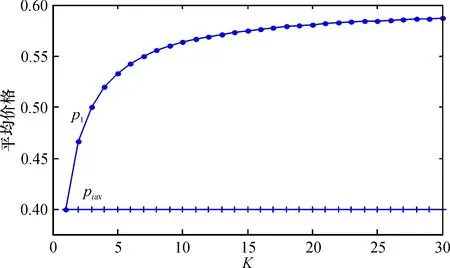
图2 商品在有歧视时先后动厂商的平均价格对比