间隙比对近壁不同钝体涡激振动特性的影响

翟少华，谢福兴，尹广洲，喜冠南

(南通大学机械工程学院，江苏 南通 226019)

流体在壁面流动时会产生边界层[1]，受边界层影响，壁面附近会出现扰动，而在近壁面插入钝体能够改变流场的流动状态.在许多工程领域中，为达到节能降耗的目的，流体在输送管道近壁区的流动一直是人们所关注的焦点问题之一[2]，例如在铺设海底输送管道时，合理设置管道与海底面的距离从而减少海水对管道的冲击破坏；在换热器的设计中，在靠近壁面处合理增加钝体从而提高换热效率等.近壁单圆柱和单方柱作为最基础的模型，其流动规律的异同点值得探究.

关于间隙比对近壁插入不同钝体绕流影响的研究，国内外学者们进行了一些试验和数值计算.圆柱或方柱与壁面间的距离L与其截面特征长度(圆柱直径或方柱边长)D的比值为间隙比，万津津[3]利用PIV对不同L/D下近壁方柱进行了试验研究，得出抑制涡街的临界间隙比在0.3～0.4，当L/D=0.1时方柱靠近壁面一侧不再有旋涡脱落，分离边界层在方柱下游7.25D处壁面再附.LEI等[4]发现壁面边界层厚度与L/D是影响绕流尾迹结构的重要参数.许慧等[5]对不同L/D下近壁单圆柱对壁面扰动影响进行了数值模拟，得出Re=200时，L/D=1.0为最佳插入位置，而Re=500时，L/D=0.6近壁区域扰动最强烈.ZHAO[6]对静态流体中近壁面振荡圆柱进行了数值模拟，发现当L/D=0.1时会显著增加阻力系数和惯性系数，若L/D=1.0或更高，与无近壁圆柱相比阻力系数变化不到10%.王国兴等[7]对不同L/D和Re下近壁圆柱绕流的水动力特性进行了数值模拟和试验研究，得出L/D较小时，涡街中线有下移趋势，尾流形态有明显的规则性和相似性.DURO等[8]通过对Re=1.4×104时不同L/D下单方柱绕流的频谱分析，得出当L/D≥1.0时出现单个明显峰值，表明涡脱落有规律性.CHEN等[9]通过对Re=200时近壁圆柱绕流横向振动的数值模拟，发现L/D≤0.5时尾流的逆时针旋涡会受到抑制，且随着L/D减小圆柱上部顺时针旋涡很强而下部逆时针旋涡逐渐减弱，另外壁面对圆柱的固有频率有显著影响.MUNIR等[10]对振荡流中近壁圆柱的流致振动进行数值模拟，发现平面边界显著影响横流方向上的振动幅度.LI等[11]研究了L/D=0，0.1，0.5时近壁圆柱尾流特性，发现涡随着L/D增大，同一符号的单列相干结构随L/D的变化而变化为偶极涡脱落增加，与固体壁面间存在复杂的相互作用.XIONG等[12]针对中、低斯托克斯数时不同L/D下的近壁面圆柱周围的振荡流进行了数值计算，确定了3种边际稳定性曲线随L/D变化的机制.

目前关于间隙比对近壁插入圆柱和方柱的研究主要集中在数值计算、湍流状态，而过渡流状态下关于两者对比的试验研究还较少，其涡激振动特性的差异还未完全研究清楚.因此，文中选取雷诺数Re=300，对近壁插入的单圆柱和方柱模型进行试验研究，分析不同间隙比L/D下两者涡激振动特性的异同点，对实际工程领域应用具有一定的参考价值.

1 试验平台与装置

1.1 试验平台

开式循环水槽试验台由水箱、调速阀、整流段、大、小蜂窝器、收缩段、试验段、过渡段、水泵等组成，如图1所示.

图1 开式循环水槽试验台示意图

水槽通过水泵从下水箱将水抽至上水箱，通过调速阀控制流速，水依次流入有大蜂窝器的整流段、收缩段.(收缩段形状通过三次方曲线拟合用于流体的加速及整流.)在收缩段与试验段连接处放置小蜂窝器用于二次整流.图2为用粒子图像测速系统[13]拍摄试验段并后处理的速度矢量图.从图中可以看出速度矢量均匀分布，表明二次整流后流场相当稳定.流体通过试验段流过模型后，为防止流体回流造成影响，设置了较长的过渡段，然后进入最右侧水箱，最后由底侧水管回流至下水箱，完成整个循环过程.

图2 试验段激光截面速度矢量图

1.2 粒子图像测速系统

图3为粒子图像测速系统PIV示意图，主要由双脉冲激光器、冷却器、CCD高速相机、同步控制器、计算机等组成.试验所用的示踪粒子是拥有较好光散射性和跟随性、密度接近于水不易沉浮、平均直径为13 μm的镀银空心玻璃球.由同步控制器同步激光频率与相机拍摄频率，双脉冲激光器通过导光臂发射出垂直于水面的片状激光，同时由垂直于试验台侧面的CCD相机拍摄激光照亮的区域，收集到的图像信息会实时传输到计算机，再通过软件进行后处理.图1中试验段的材料为光滑透明的亚克力玻璃板，当激光的片光垂直照射在壁面时，能够最大限度允许光的透射，有效抑制了壁面反光引起的光学污染[14].

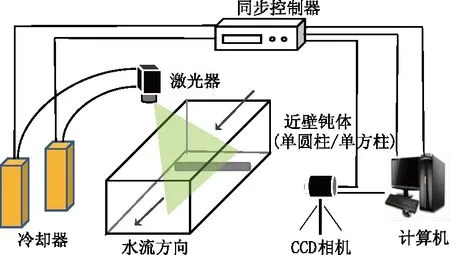
图3 试验台PIV系统示意图

1.3 试验模型与参数

本研究中，雷诺数计算公式为

(1)

式中：ρ为流体密度；Um为平均速度；D为模型特征长度；μ为黏性系数.

试验模型布置如图4所示，图中U为进口速度，D为钝体特征长度(圆柱的直径或方柱的边长)，L为钝体下边缘距壁面的距离，L/D为间隙比.试验中，Re=300，D=15 mm，水温T=20 ℃.双脉冲激光器的频率为20 Hz，每个工况拍摄400张照片，分别对L/D为0.2，0.4，0.6，0.8，1.0进行分析.

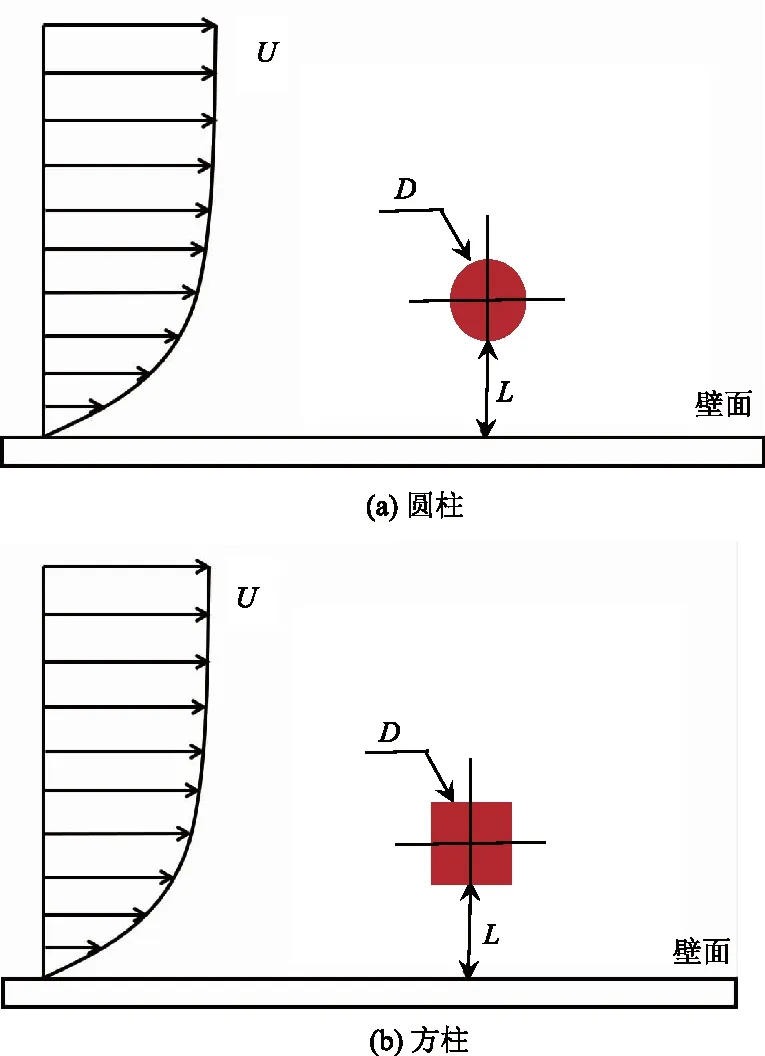
图4 模型的试验布置和参数设置

2 试验结果分析

2.1 时均流场分析

考虑到时均特性的一般性特征，对2种模型尾流的时均流场及涡量进行对比分析.在流场中，涡激振动特性变化主要变现为尾流处分离剪切层的变化以及涡的尺度变化.涡量一般定义为流体速度矢量的旋度，其中蓝色表示负涡，引导顺时针流动；红色表示正涡，引导逆时针流动.颜色的深浅程度表示涡量强度的大小，涡激振动特性变化表现为涡量分布区域大小和涡量的强弱变化.两者的时均流场图及涡量图分别如图5，6所示.

图5 不同L/D下模型的时均流线及速度场图

在同一Re，不同L/D下，如Re=300，L/D=0.2时，流体流过钝体表面形成双侧分离剪切层，上侧剪切层形成顺时针回流，涡量强度较大.此时间隙较小，下侧剪切层发展受到抑制，经过间隙流体的流速加快，在钝体后侧近处形成强度较小的逆时针负涡，在较远处形成了顺时针回流区.当L/D=0.4，0.6时，上侧顺时针正涡的强度较L/D=0.2时减小，间隙增大使得下侧分离剪切层慢速发展，逆时针负涡强度增大，与上侧正涡构成旋涡对.近壁方柱后侧近处的旋涡对尺度更大，远处正涡尺度较L/D=0.2略微增大且逐渐贴近壁面.当L/D=0.8时，壁面的抑制作用减弱，后侧形成旋涡对的尺度以及涡量强度逐渐增大.相比于同工况的近壁圆柱，方柱后侧旋涡对尺度更大.当L/D=1.0时，壁面的抑制作用进一步减弱，钝体后侧旋涡对趋于对称，而尺度以及涡量强度较L/D=0.8相差不大，与无壁面时的特性相似，说明壁面对钝体绕流的影响较小.

图6 不同L/D下模型的时均涡量图

2.2 速度截面分析

为研究不同L/D对壁面流动不稳定性的影响规律，结合时均速度截面分布进行分析，3个截面位置分别选择X/D=1.5，3.0，4.5处.

当Re=300时，不同X/D下的2种模型的速度截面分布如图7所示.当L/D=0.2时，间隙较小，近壁面区域流动加速，但是壁面的抑制作用强，加速效果不明显；当L/D=0.4，0.6时，圆柱后侧远处顺时针回流区消失，近壁面流速明显加快，而方柱壁面附近流速变化不明显；当L/D=0.8时，间隙继续增大，抑制作用的减弱使近壁面流速继续增大，此时方柱后侧远处顺时针回流区消失，近壁面附近流速明显增大；当L/D=1.0时，壁面的抑制作用进一步减弱，下游剪切层充分发展，近壁面附近流体加速效果达到最强.

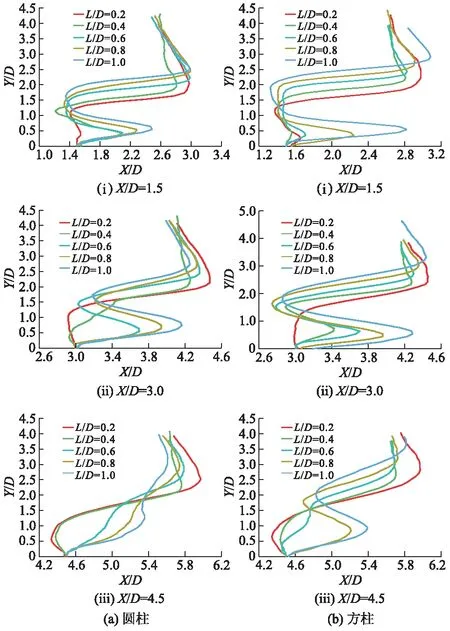
图7 不同L/D下圆柱和方柱后侧截面的速度截面分布图

当L/D=0.2时，X/D=3.0正处于远处顺时针回流区边缘，受其影响，两模型壁面附近流速几乎为0，此时壁面扰动较弱.当L/D=0.4时，抑制作用减弱，圆柱近壁面流速变化不明显，而远处顺时针回流区消失导致圆柱后侧流速大幅增加，此时方柱壁面附近流速也明显加快.当L/D=0.6～1.0时，抑制作用逐渐减小，两模型壁面附近流速逐渐增大，在L/D=1.0时达到最快.

当L/D=0.2，0.4时，X/D=4.5处于远处顺时针回流区附近，两者近壁面附近流速出现负值，壁面附近出现回流；当L/D=0.6时，圆柱后侧流速随着与壁面垂直距离增加而增大.而方柱远处仍然存在顺时针回流区，壁面流速无明显变化，且方柱后侧流速比同位置圆柱的更小；当L/D=0.8，1.0时，方柱在X/D=4.5处流速曲线与X/D=1.5，3.0相似，而圆柱此处流速随着间隙增大而增大.这是由于相同工况下，X/D=4.5处圆柱后侧旋涡对尺度更小，对此处流速影响也更小，使其逐渐接近主流区流速.

2.3 瞬态周期流动特性

过渡流状态下的流场具有周期性变化规律[15]，对两者的流动周期性进行分析.选取L/D=0.2，0.6，1.0时分析尾流监测点A在y方向速度随时间的变化特征.为准确监测到壁面附近的流动情况，监测点选在与钝体中心的横向距离X=2.5D处，垂直距离y随L/D变化.

图8，9分别为不同L/D下监测点A在y方向上的速度随时间变化波动图(v-t)、功率谱密度图(PSD-f).可以看出，当L/D=0.2时，两者的v随t在水平轴线附近无规律变化且振幅较小，对应的能量谱密度也在多频率下出现不同峰值，表明此时流体的涡激振动没有周期性特征.

图8 不同L/D下的2种模型的速度波动图

图9 不同L/D下2种模型的功率谱图

当L/D=0.6时，圆柱v振幅增大，而方柱变化不明显.随t变化，两者v都表现出了周期性规律，圆柱和方柱对应的功率谱密度分别在频率为1.5，1.2 Hz左右处出现了单一峰值，表明两者分别形成了振动主频率约为1.5，1.2 Hz的周期性振动.当L/D=1.0时，两者v的振动仍然保持周期性特征、主振频率都略微减小，但方柱振幅进一步增加，壁面附近的扰动程度增强，而近壁圆柱v振幅比之前减小.

总体上，随着L/D增大，圆柱尾流处振幅先增强后减弱，主振频率逐渐减小；而方柱的振幅逐渐增强，主振频率也逐渐减小且主振频率略微小于圆柱，这表明近壁单方柱绕流周期比单圆柱周期更长.

以上分析表明两者具有周期性流动特征，选取L/D=1.0工况具体分析两者在1个流动周期内瞬态流场的变化特点.图10为Re=300，L/D=1.0时1个流动周期内6个不同时刻的流场图.

图中黄色和蓝色箭头标记分别表示上、下侧分离剪切层产生的顺时针正涡和逆时针负涡.可以看出，刚开始时，正涡初步形成，随着不断发展，其尺度不断增大且逐渐向钝体后侧远处移动，最终完全消失；与此同时，负涡也经历了由形成、发展至脱落的过程，在钝体尾流处表现出正、负涡规律的交替脱落现象.这可以说明由于钝体尾流的周期性的涡脱运动，使壁面间的流动不稳定性增强.

图10 L/D=1.0时1个流动周期内不同瞬时的流线及速度

3 结 论

1) 近壁单圆柱与单方柱尾迹有着较为相似的涡激振动特性.①L/D较小时，钝体下侧剪切层发展受到抑制，上侧剪切层在远处形成大尺度顺时针回流区域;② 随着L/D增大，壁面的抑制作用逐渐减弱，钝体后侧近处由逆时针单涡逐渐演变成对称的旋涡对，旋涡逐渐靠近钝体，涡的尺度先增大后减小，远处顺时针回流区域逐渐消失;③ 钝体近壁面附近流体的加速效应而先增强后减弱，且主振频率逐渐减小；另外，钝体尾流表现出了周期性的涡脱运动，使其与壁面间的流动不稳定性得到增强.

2) 近壁单方柱绕流与近壁单圆柱也存在差异.① 方柱的涡分离点固定，而圆柱没有固定分离点，同一Re，相同L/D工况下方柱涡的尺度以及涡量强度比圆柱更大，方柱近壁面附近流速也更快；② 随着L/D增大，近壁圆柱尾流处振幅先增强后减弱，方柱尾流处振幅逐渐增强且主振频率略小，表明近壁单方柱绕流周期大于单圆柱.