高海况下反舰导弹对舰船目标攻击策略

但 波，宋伟健，高 山，翟龙军

（海军航空大学，山东烟台 264001）

反舰导弹攻击水面典型舰船目标时，通常根据目标的散射特征数据进行目标类型判定并做出是否进行攻击的决策[1-3]。相对于反舰导弹末制导雷达导引头的工作频段而言，水面舰船等大型目标属于电大尺寸目标，雷达反射截面积（Radar Cross Section，RCS）通常很大[4-5]，容易被导弹末制导雷达导引头锁定。但是当舰船在海面行进过程中，由于海况多变以及多路径的耦合效应，导致舰船目标的RCS出现起伏甚至突变[6]，从而影响了导弹的判断和决策。不同航行方向和不同海况下，浪高、破碎浪等对舰船RCS 产生的影响不同[7]，根据舰船行驶方向与海浪方向，可分为舰船横浪行驶和顶浪行驶。

本文主要从海面和舰船相对运动关系出发，仿真研究了高海况情形下舰船RCS的分布特性，为导弹在不同海况下对海面舰船实施攻击方向的选择提供参考依据。

1 仿真算法

目标的散射特性数据通常通过实际测量或实验室仿真2种方法获得。实际测量方法受目标模型的有效性和测试场地局限性等因素影响，最终导致无法被广泛应用。而实验室仿真是依据电磁波传播和目标散射的理论，采用建模仿真的方法，它是获取目标（尤其是非合作目标）散射特性高效可靠的途径[8]。在计算电磁学领域，对于电大尺寸模型，低频算法由于对硬件要求高、计算效率差等因素无法被广泛应用。高频算法则由于做了近似处理，在保证精度的同时可以快速完成仿真计算。在众多高频算法中，弹跳射线算法（Shooting and Bouncing Ray，SBR）是精度和效率结合最好的计算方法[9]，本文拟采用SBR 算法对目标进行RCS的仿真计算。

SBR 算法是结合了物理光学（Physical Optics，PO）法和几何光学（Geometric Optics，GO）法优点的高效精确高频算法[10]，适用于电大尺寸目标的计算。SBR 算法，是根据GO 算法的反射求解规则进行射线的追踪，再通过PO 算法求解观察方向的散射远场。这种算法理论通俗易懂，易于编程实现、计算结果准确度较高。SBR 算法的射线追踪过程与图形计算的光线追踪过程类似，首先，根据雷达波入射方向在目标的周围构建虚拟孔径面，射线之间的间隔与仿真计算频率相关联。然后，对所有的射线跟踪计算，依据算法中设置的遮挡和相交规则，判定追踪结果。如果射线管和目标某些面元相交，则根据GO 算法的反射原理计算反射强度。判断当前面元如果为照亮区域，则根据PO 算法求解出当前区域上的感应电流，最后积分求解雷达观察方向散射场。所有射线管散射场的远场叠加结果即为目标的散射总场。SBR 方法相比于其他高频方法计算准确度高，因此获得了更多科研工作者的青睐。散射总场的具体表达式为：

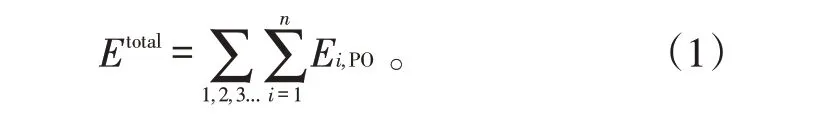
式（1）中：第1个求和符号表示对所有射线的散射总场求和；第2 个求和符号表示对不同反射次数下被照亮区域的面元的散射场求和；n表示不同反射次数追踪过程中亮区的面元数量。由于SBR算法是结合了GO和PO算法，现将GO和PO算法简介如下。

1.1 GO算法

GO 算法处理电磁波传播时模拟成射线传播过程，这种处理方法的优点是可以直接利用反射、直射和折射的原理进行计算，GO算法示意图，如图1所示。

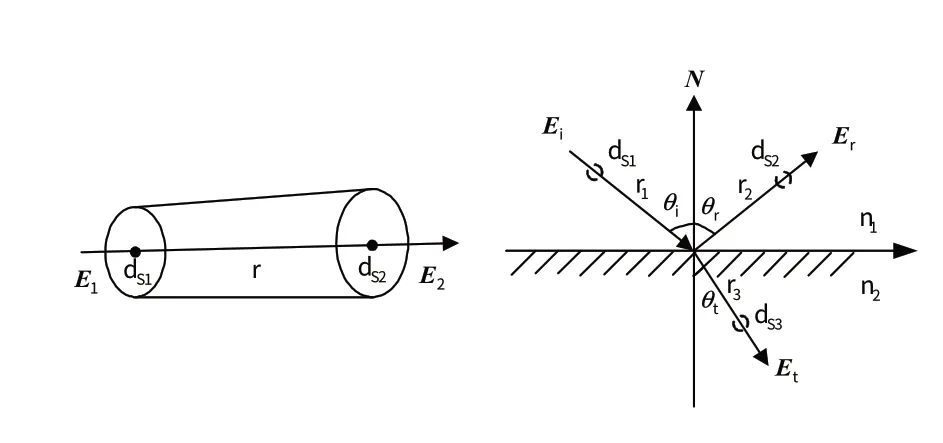
图1 GO算法示意图Fig.1 Geometric Optics method

当频率很高时，电磁波的波动对传播影响很小，因此，可以将电磁波的传播用几何光学的反射定律来表示，即沿1个射线管的总能流为常数，如式（2）所示：

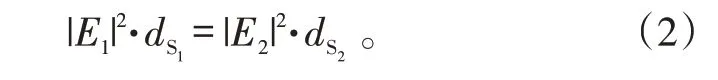
电磁波的场强是随着射线方向的改变而变换的，这种改变需要用几何光学的强度定律来计算。带入式（2）中，可得到电场在媒质中传播的表达式，

式（4）（5）中：Rhv和Thv分别为反射系数和透射系数；dS1、dS2、dS3分别代表入射射线管、反射射线管以及透射射线管的横截面积；r1、r2、r3代表入射、反射和透射射线管的路径长度。根据费马定律计算射线在多层媒质中的传播方向，以此确定在媒质分界处的射线反射角与折射角，从而计算射线的传播路径。

1.2 PO算法

PO 通过求得目标散射场的积分，来计算目标的远场特性，它是根据Stratton-Chu 场积分方程来计算的。通过确定目标边界条件，并应用近似式n×Htotal=2n×Hincident，可求得远场条件下接收到的目标散射场为：

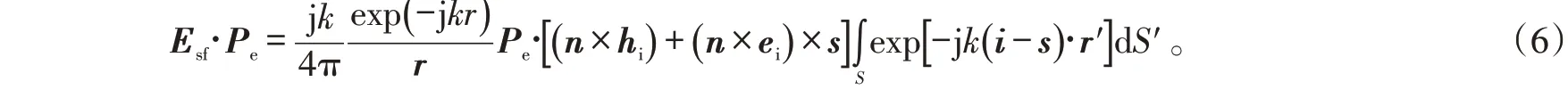
式（6）中：exp[- jk(i-s)∙r′] 为雷达相对于面元位置产生的相移；Esf为面元表面的散射场；Pe为接收电场的极化单位矢量；k为波数，且k=2πλ；n为面元的单位外法向量；ei、hi分别为入射电磁场的极化方向的单位矢量；i、s分别为入射和散射传播方向上的单位矢量；r′为面元相对于雷达天线的位置矢量。

在求得目标面元的散射场后，代入RCS 定义式，即可求得通过PO 法求解的面元复RCS 矢量，所有面元计算结果叠加后得到目标的总RCS值，总RCS值公式如下：

式（7）中，σfacet为计算RCS值。

1.3 电大尺寸目标RCS计算

本文采用在计算电大尺寸目标中具有效率优势的SBR 算法进行目标RCS 的仿真计算。SBR 算法计算精度与多次反射次数和射线密度相关[11]，通常情况下，多次反射次数为3次，射线间隔为1/10波长。舰船某角度下多次反射示意，如图2 所示。根据多次反射的射线追踪结果进行面元的积分和叠加，可以得到目标的RCS结果。

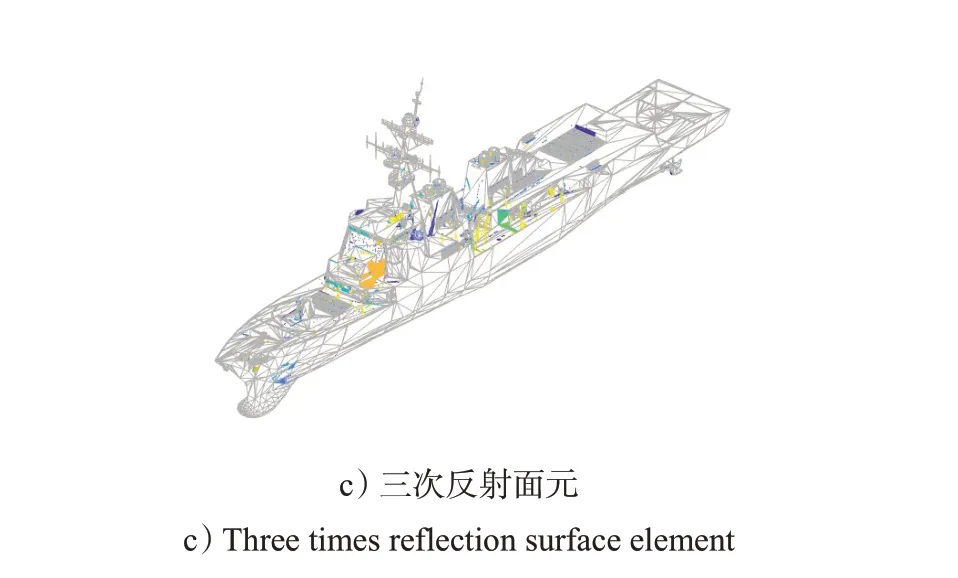
图2 舰船目标模型Fig.2 Model of target ship

2 物理模型建立

2.1 舰船建模

迈克尔·墨菲号导弹逐舰（DDG112）长153.6 m，宽19.2 m，高52.6 m，以该舰为原型进行仿真建模，模型如图3所示。

图3 舰船目标模型Fig.3 Model of target ship

2.2 海面建模

风、气压、天体引力、海洋不同水域密度差等因素可以形成海洋波浪，而绝大多数波浪是直接由海面风吹动引起的，这种波浪表现为海面连续变化的紊乱的波峰和波谷，波形无规律可言，传播方向也变化莫测[12-13]。海面建模方法主要分为基于几何构造建模方法、基于运动模型建模方法、基于频谱统计模型建模方法和基于物理模型建模方法[14-15]。

1）基于几何构造建模

基于几何模型的海面建模是由参数控制方程和构造函数，模拟生成海面的高度场。此方法理论模型主要有凹凸纹理映射模型（bump mapping）、Perlin 噪声模型、Gerstner-Rankine 模型、Stokes 模型、Peachy 模型。

2）基于运动模型建模

基于运动模型的海面建模是把海面分割成众多的细小粒子，根据粒子的运动模型，生成具有代表性的海面高低起伏状态，此方法包括元胞自动机模型和粒子系统模型。

3）基于频谱统计模型建模

海洋学领域有多种海浪谱形式，如PM海谱、Fung海谱、JONSWAP海谱等[16]，这些经典图谱都是以正弦波的叠加结果来模拟海面，通过快速傅立叶变换，计算得到有限区域高度场来模拟海谱的分布。基于海谱模型构建的双尺度海面，如图4所示。

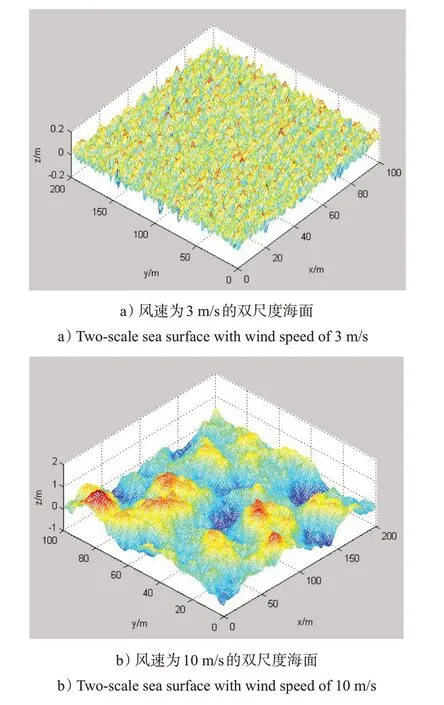
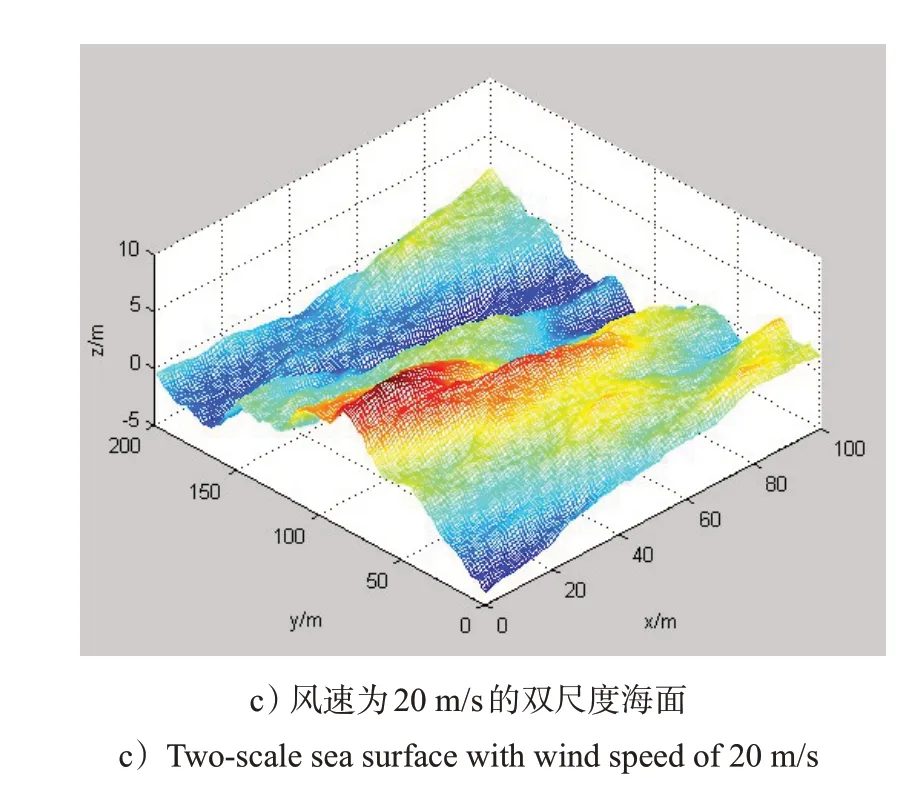
图4 基于频谱构建不同风速海面Fig.4 Sea surface with different wind speeds based on the frequency spectrum

4）基于物理模型建模

基于物理模型的方法是图形学领域的研究热点。原理上根据经典流体力学方程（Navier-Stokes equations，简称N-S 方程）来模拟海面模型，N-S 方程可以表征任意位置和时刻的流体运动特性，计算方程获得的解可用来表征海洋表面的运动特征。该方法构建的海面物理模型，如图5所示。

图5 基于物理模型构建海面Fig.5 Sea surface based on physical model

由于基于物理模型建模方法构建的海面连续，符合海面流体运动的规律，生成的海浪接近海面真实的物理现象[17]，因此，本文海面建模采用的是基于物理模型建模的方法。

2.3 舰船海面融合模型

舰船海面融合主要是将舰船模型和海面模型根据相对位置关系进行组合，并定义不同的材质参数[18-19]，支持后续的仿真计算。海面舰船融合后场景，如图6所示。

图6 海面舰船融合模型Fig.6 Fusion model of sea suface ship

根据舰船和海浪的相对位置关系，主要分析舰船位于波峰和波谷2种状态。而位于波谷时又分为舰船顶浪和横浪航行。舰船位于波峰、舰船位于波谷顶浪航行和横浪航行情况下海面舰船融合模型分别如图7～9所示。

图7 舰船位于波峰Fig.7 Ship at the sea crest

图8 舰船顶浪航行Fig.8 Ship sailed in heading waves

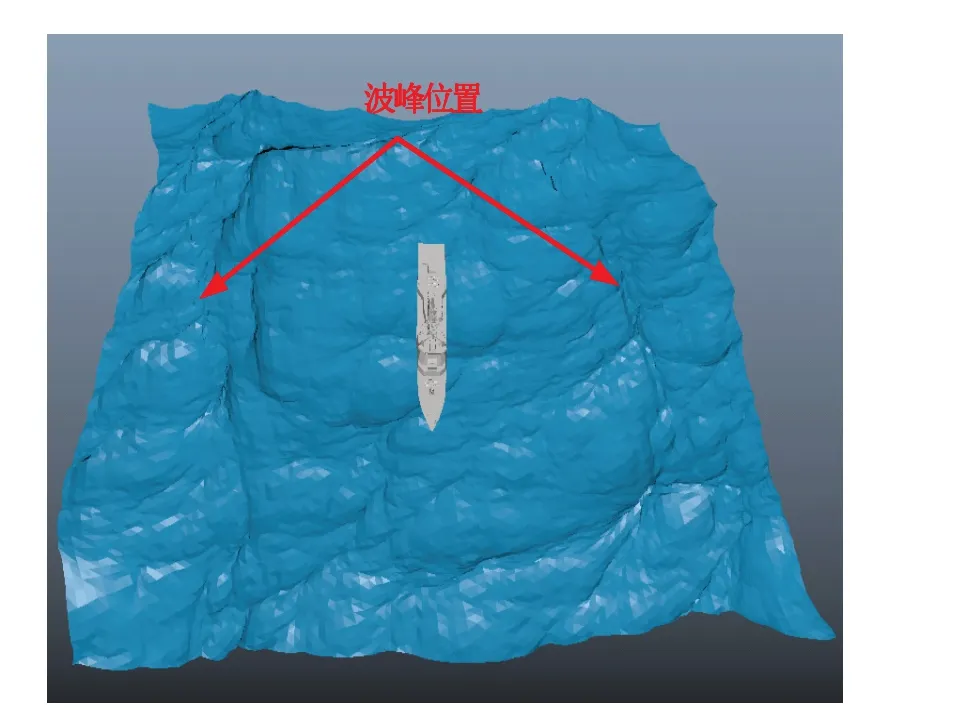
图9 舰船横浪航行Fig.9 Ship sailed in beam waves

3 仿真计算

本文采用电磁SBR 算法计算在单站方式下的舰船目标海面背景的RCS 数据，极化采用VV 极化的方式，仿真的坐标系示意，如图10所示，其中船头方向为X轴（对应俯仰角为90°，方位角为0°），船身侧面为Y轴（对应俯仰角为90°，方位角为90°），Z轴为天顶方向（俯仰角为0°）。

图10 仿真坐标系示意Fig.10 Simulation coordinate system

仿真计算条件设置，如表1所示。

表1 仿真条件设置Tab.1 Simulation conditions

本文主要模拟了舰船无海面背景、舰船位于波峰、舰船位于波谷顶浪航行和舰船位于波谷横浪航行4 种状态下的RCS 分布情况。为了便于说明，只利用VV数据显示舰船目标在不同航姿下水平面全向RCS结果，仿真结果如图11～14所示。

图11 无海面背景下目标RCS曲线Fig.11 Curve of the RCS of the ship without sea background

从图11 可知，采用SBR 算法计算得到的RCS 可准确反映目标舰船的散射分布特性，舰船较强的散射方向出现在了船身两侧和船尾位置，船头和其他方向相对弱些。船身两侧和船尾的散射较强，主要是由于该方向出现了类似镜面反射的效应，而船身两侧的RCS 数值差异主要是由于船身的不对称性所引起。由舰船RCS分布特性可知，导弹进行攻击时选择船身两侧更容易命中目标。

从图12 可知，当舰船位于波峰时，海浪的起伏会引起舰船RCS的变化，主要的影响出现在RCS相对较小的角度上，而船身两侧和船头船尾位置，由于舰船自身RCS较大，海浪的影响相对较弱，因此，当船位于波峰时，由RCS 分布特性分析可知，导弹选择船身两侧攻击更容易命中目标，攻击方向如图15所示。

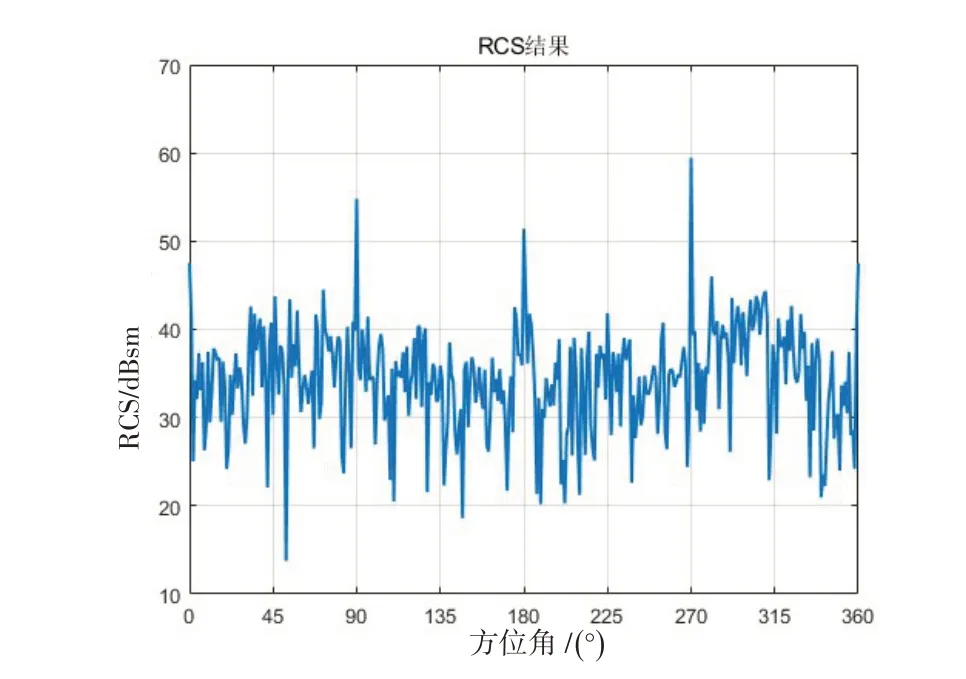
图12 舰船位于波峰RCS曲线Fig.12 Curve of the RCS of the ship at the sea crest

图13 舰船顶浪航行RCS曲线Fig.13 Curve of the RCS of the ship sailed in heading waves

图14 舰船横浪航行RCS曲线Fig.14 Curve of the RCS of the ship sailed in beam waves

图15 导弹攻击航路选择Fig.15 Choice of attack route

从图13 可知，当舰船顶浪航行时，如果舰船位于波谷位置，此时海浪对舰船RCS的影响主要体现在船头和船尾方向，舰船侧面由于受海浪影响较小，只是会有较小的波动，影响不会明显的降低，此时，如果导弹选择船身两侧进行攻击，则受海况影响较小，可大概率提高命中率。因此，建议选择从船身侧面进行导弹攻击，如图16所示。

图16 导弹攻击航路选择Fig.16 Choice of attack route

从图14 可以看出，当舰船横浪航行时，海浪随机起伏，当舰船位于波谷时，由于海浪的高度对船身有一定的遮挡效应，舰船和海面的相互耦合作用影响了船身侧面的RCS，此影响随海浪的高度，相对位置等随机产生，船身侧面的RCS 降低明显，船头和船尾影响相对不大，但要比船身侧面的RCS 值大，此种情况下，如果选择攻击船身，导弹容易受海浪影响，造成脱靶现象。因此，应该选择船头或船尾位置进行导弹攻击，如图17 所示。需要注意的是，在高海况下舰船一般是顶浪航行，舰船在横浪航行情况下，导弹攻击方向亦可参照此分析。

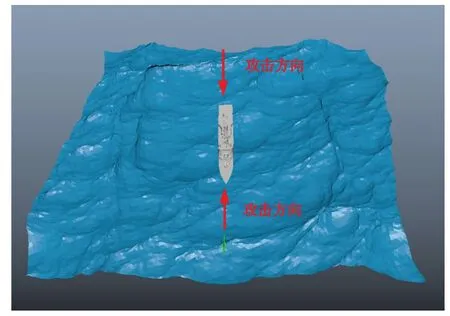
图17 导弹攻击航路选择Fig.17 Choice of attack route

4 结论

本文主要从海面和舰船相对运动关系出发，仿真研究了高海况情形下舰船位于波峰、波谷顶浪航行和波谷横浪航行几种典型状态下的RCS 分布特性。根据仿真计算结果可知：当舰船位于波峰时，海浪对舰船的RCS 影响相对较小，如果选择船身两侧进行攻击，则大概率会命中目标；当舰船位于波谷顶浪航行时，海浪对舰船RCS的影响主要体现在船头和船尾方向，舰船侧面由于受海浪影响较小，不会出现明显的影响。此时，如果导弹选择船身两侧进行攻击，则受海况影响较小，可大概率提高命中率。当舰船位于波谷横浪航行时，船身侧面的RCS 降低明显，船头和船尾影响不大，且比船身侧面的RCS值更大，因此，应该选择从船头或船尾位置进行导弹攻击。此研究结论可为导弹在不同海况下对海面舰船实施攻击方向的选择提供参考依据。