乘用车城市综合工况设计方法研究

霍海涛 张鑫 刘元治 张强 马腾 马沫凯

（1. 中国第一汽车股份有限公司 新能源开发院，长春 130013；2. 汽车振动噪声与安全控制综合技术国家重点实验室，长春 130013）

主题词：工况设计 新能源汽车 乘用车

1 引言

目前，世界各国都有本国法规规定的适用于本国的车辆道路循环工况，如业内熟知的欧盟车辆道路循环工况NEDC、日本的车辆道路循环工况10.15、美国的车辆道路循环工况FTP-75 以及中国的中国工况CATC，这些车辆道路工况在世界各地被广发采用。

上述这些工况覆盖的范围主要是国家重点城市，其开发车辆有明确投放目标市场/城市，其代表性不足以支持车辆的经济性开发。本文主要针对开发车辆的目标投放城市，进行针对性的工况设计，用于支持开发车辆投放目标城市的代表工况的经济性优化[1-4]。

2 关键原理研究

2.1 工况特征值

2.1.1 工况特征值确定

汽车行业表述工况的普遍方法是用时间与车速的曲线，但实际上，单从车速这一个维度很难完整的表述一个工况的所有行驶特征。

本文采用李宁在《城市道路车辆行驶工况的构建与研究》[5]中提到的特征值构成方法，计算2部分特征值：

（1）各个运动学片段的特征值;

（2）整体实验数据的特征值。

通过运动学片段特征值的分析（主成分分析、聚类分析），构建目标行驶工况，通过对比目标行驶工况与整体实验数据的特征值的误差，来决定构建的目标行驶工况对目标城市实际道路工况的代表性。该误差超出一定范围，即可认为所构建的道路循环工况无法代表实际的车辆道路循环工况。

按照这种准则，选择误差范围最小的车辆道路循环工况代表车辆实际循环工况。

本研究方法采用的运动学片段特征值构成为：行驶时间、行驶距离、平均车速、最大车速、车速标准差、加速段平均加速度、最大加速度、加速段标准差、减速段平均减速段、最大减速度、减速段标准差、加速比例、减速比例、匀速比例、怠速比例、RPA，表1 列出共计16个特征参数，这些特征参数即表示运动学片段或者城市实际道路工况的行驶特征。

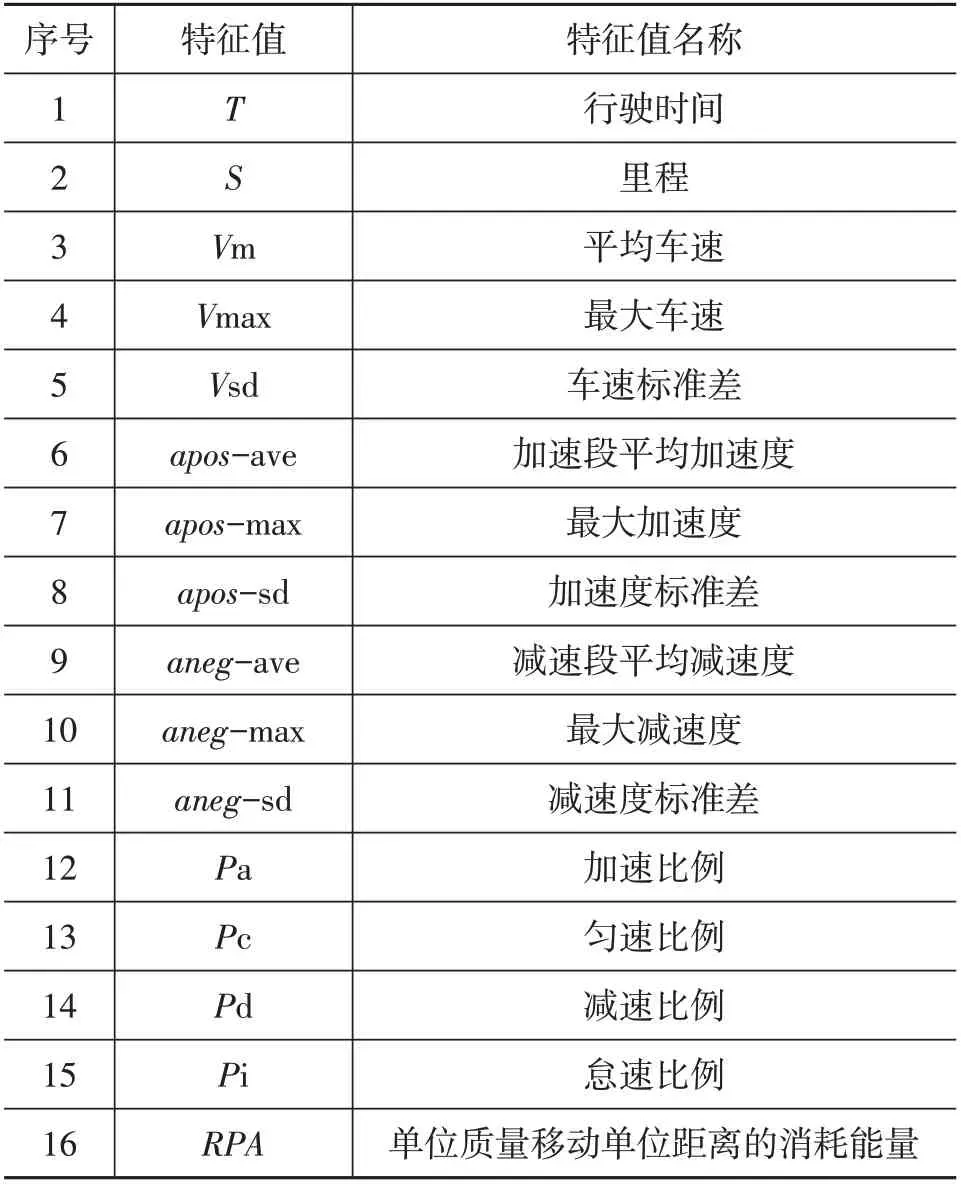
表1 工况特征参数

2.1.2 工况特征值相关性

如上文所述，构成各运动学片段或道路工况的各个工况特征值表征了车辆实际道路循环工况的行驶特征，换言之每个特征值都提供了该运动学片段、道路工况的某些信息，即如上16个特征值可以认为是车辆道路循环工况构建的依据，这些特征值随着城市道路的不同、实际环境的变化，其所代表的形式特征也将有相应的变化，当然这些信息可能存在重叠、一定程度上的相关性，比如行驶时间、最大车速、平均车速之间存在一定的相关性或者特征重复性等[6-9]。

2.2 主成分分析原理

主成分分析是一种统计学方法，通过线性变换将一组线性相关的变量（指标）组合变换成另一组不相关的相互独立的变量（综合指标），用较少的变量来代替原来较多的变量，生成的新变量称为主成分。

通过对采集到的大量车辆运行工况数据进行筛选和运动学片段的划分可以得到运动学片段的总体样本，然后通过计算得到运动学片段总体样本的特征参数值。可以利用SPSS 软件中的因子分析对特征值参数进行主成分分析，达到对特征值变量进行降维处理的目的。

由于各个特征值变量量纲不同，在主成分分析前需要对原始特征值变量进行标准化处理，通过主成分分析得到了各个主成分的特征值、贡献率和累计贡献率，总方差解释表。

2.3 聚类分析原理

聚类分析(Cluster analysis)是一种将研究对象分为相对同质的群组(Clusters)的统计分析技术[10]。

本文采用划分法进行聚类分析，首先指定部分数据作为聚类中心，然后通过反复迭代来改变分组，每次分组的改变将其他数据向事先指定的中心类数据靠近，直至聚类中心点收敛。由于本文直接使用Spss软件完成的数据分析，在此不对聚类分析做详细的介绍。

在典型工况制定中，可以按照各个运动学片段的主成分综合得分进行聚类，即利用“主成分相应特征根的平方根与特征向量的乘积为因子载荷量”的性质，进行主成分变量的表达式编辑，得到主成分的表达式。

3 运动学片段

运动学片段是车辆从一个怠速开始到下一个怠速开始的行驶片段（包括前一个怠速时间阶段）。王军方等[6]提出运动学片段分类方法，本文将运动学片段分为4 个行驶状态：怠速状态、加速状态、减速状态及匀速状态，且每个运动学片段的时间>20 s，如图1。

图1 运动学片段

3.1 运动学片段设计原则

从车辆道路循环工况大数据中提取数据合成代表工况需要运用短行程法构建，所以起始阶段需要进行运动学片段的划分。

不包括运动学片段所包含的4个行驶状态的片段应予以舍弃；存在较长断点的数据应予以舍弃。

3.2 运动学状态划分定义

数据处理注意事项：加减速度的选取以加速度的阈值作为划分原则，目前国内外将运动学片段的运动学状态划分为3 种方式（如表2），本方法在对所采集数据的加速度进行数值统计分析的基础上，实施方案采用第1种划分方式。

表2 运动学状态划分种类

3.3 运动学片段分类

为了达到支持车辆经济性优化的目的，合成的工况需要根据所有运动学片段的速度、加速度的大小进行分类，以使经济性的策略优化更加具体。据此，按照表3对车辆道路循环工况的大数据进行分类。

3.4 设计步骤预览

第1 步，工况设计的初期应该建立行驶工况数据库，并处理奇异点删除无效片段；

第2 步，使用已建立的工况数据库进行运动学片段的生成；

第3步，分别计算各运动学片段的特征值；

第4 步，按照表3 的分类方法将所有运动学片段分为6类；

表3 运动学片段的分类

第5步，各类运动学片段依次进行主成分分析，即将原来变量重新组成一组新的无相关性的若干综合变量，同时根据需要从中取出几个较少的综合变量尽可能多地反应原变量的信息；

第6 步，设计分类总数并使用已有的主成分进行聚类迭代；

第7 步，使用各类片段中靠近欧式中心的运动学片段进行组合，形成合成工况。

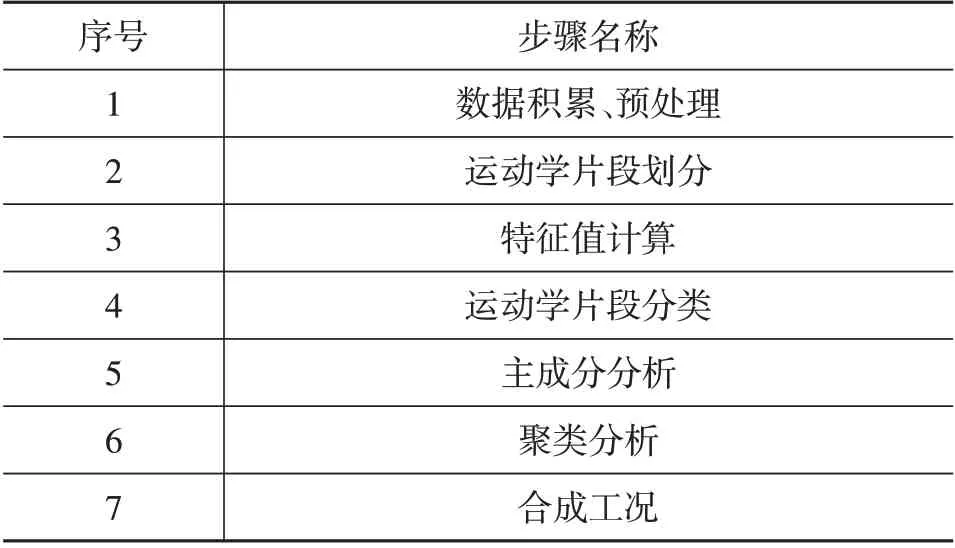
表4 工况设计步骤简述

3.5 数据源特征

3.5.1 数据源信息简介

本文使用的数据来源于出租车行驶数据（GPS 采集）、企业员工私家车上下班数据（行车记录仪采集）、自主设计代表性路线的企业试验车辆行驶数据（行车记录仪采集）、郊区行驶数据等。

表5 数据源基本信息

由以上的所有数据构成了本文进行工况合成设计的数据源，此过程中需要注意将数据的采样频率统一调整为10 Hz。

3.5.2 数据源特征计算

首先，按照下面（1）～（7）的步骤进行数据的预处理。

（1）将车速≤1 km/h的车速点修正为0 km/h；

（2）将车速>150 km/h 的车速点修正为其前一时刻的车速；

（3）加速度>4 m/s2的车速点修正为加速度为3 m/s2的车速点；

（4）减速度<-5 m/s2的车速点修正为加速度为3 m/s2的车速点；

（5）去除<4 km/h的蠕动车速点；

（6）去除>5 min的怠速点；

（7）统一数据的采样频率为1 Hz，统一频率过程中若出现某租数据循环的最后一点车速大于0，则给该组数据的最后时刻添加一个0车速点。

数据预处理完成后，按照表1 中列出的工况行驶特征参数，计算数据源的所有运动学片段的行驶特征，如表6 示列出了高速2 类数据源的行驶特征参数。

表6 2类高速数据源的行驶特征

下面以高速经济型数据源合成最终工况的过程，来说明合成工况的成果。

3.5.3 数据源特征相关性

通过SPSS 软件，针对高速经济型数据源，计算如表1 所示的16 个行驶特征参数的相关性，结果如表7所示，表中各数值均为相关系数，无单位，系数越接近1代表相关性越大。

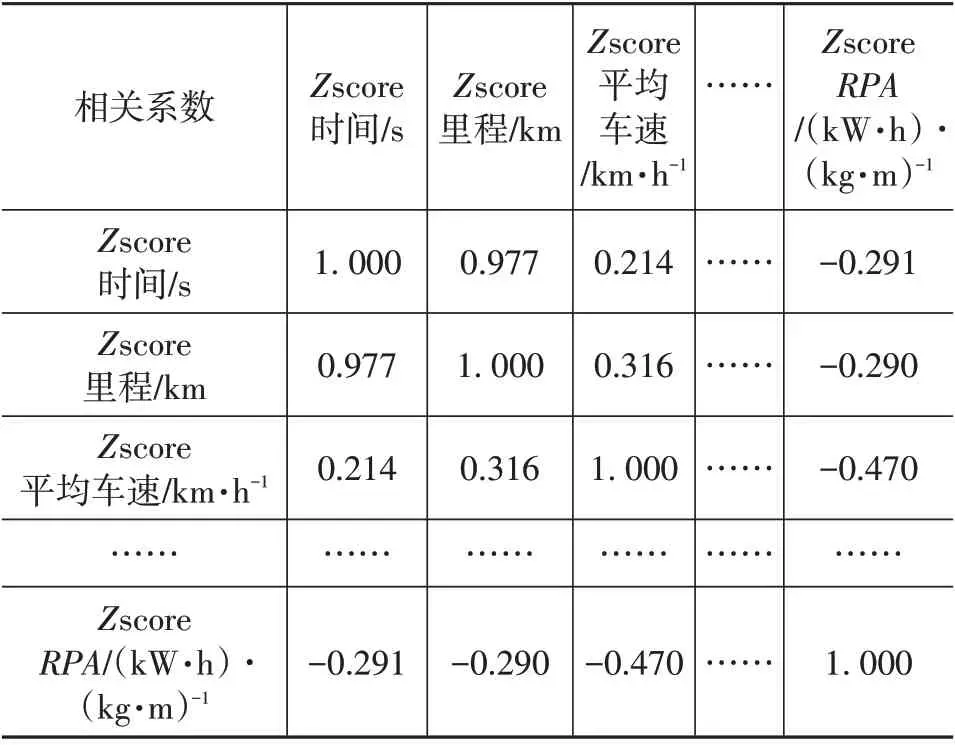
表7 特征参数相关性结果展示

由计算结果可知，各特征参数之间存在一定的相关性，且里程、平均车速、与最大车速与其他特征参数间的相关性相对较大。此结果验证了主成分分析的必要性。

3.6 主成分分析

通过SPSS 软件，依次计算主成分方差、因子载荷矩阵，可得到组合后的新运动学特征参数与原变量的对应系数，结果如表8所示。

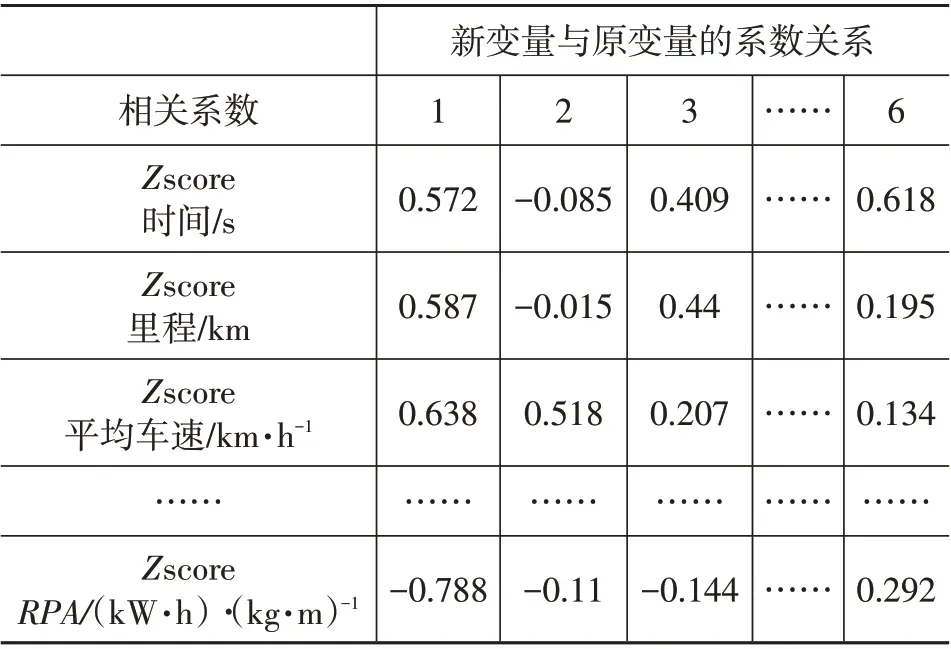
表8 运动学特征参数的相关系数

因子载荷矩阵表达的是运动学特征参数与主成分的相关性载荷矩阵，若某个特征参数在其主成分上的绝对值越大，即表示此特征参数与该主成分的相关性越高。如表8可以看出，里程、平均车速、最大车速在各主成分中的参与系数为最高。

3.7 聚类分析

通过建立新的主成分表达式，并在SPSS 软件上计算各新的主成分的贡献率。通过SPSS 软件计算聚类数分别为2、3、4、5、6、7、8 时类内距离大小（表9），当Xi≤X2×10%（Xi为聚i类时的类内距离，X2为聚2类时的类内距离）时，认为聚类数合适，由下表知聚类数应选择8类。

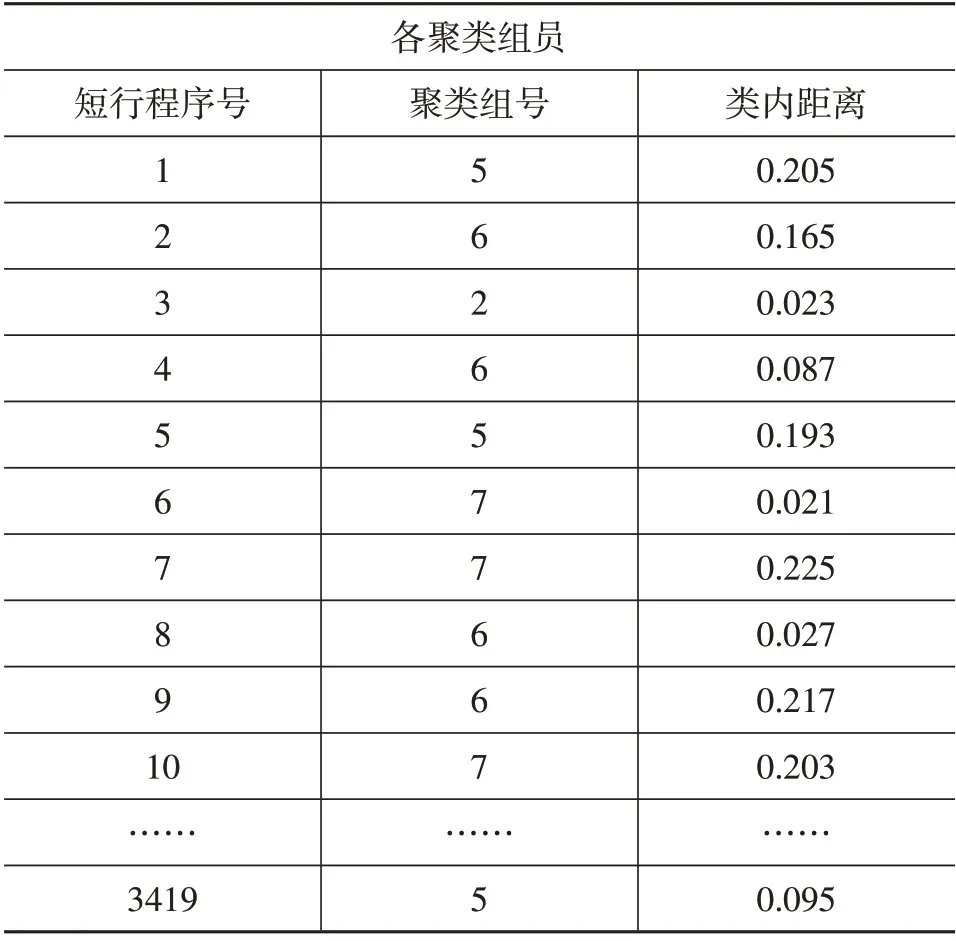
表9 不同聚类数量的类内距离结果

3.8 合成工况

按照每一类微行程的总时间/所有微行程（如：高速经济型）总时间这一比例，选择每一类微行程中欧式距离尽量小的微行程，然后组合成工况。最终合成的6类工况，如图2。

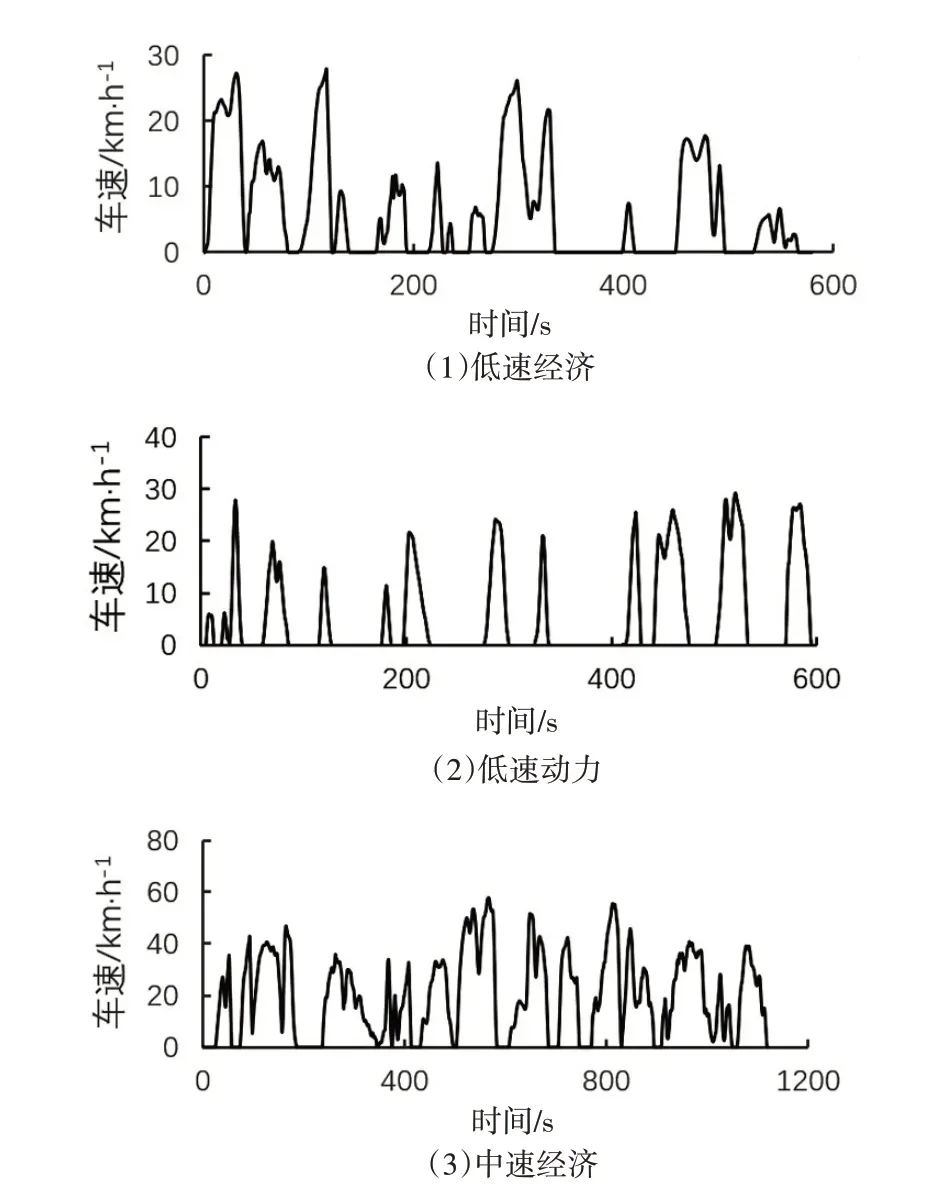
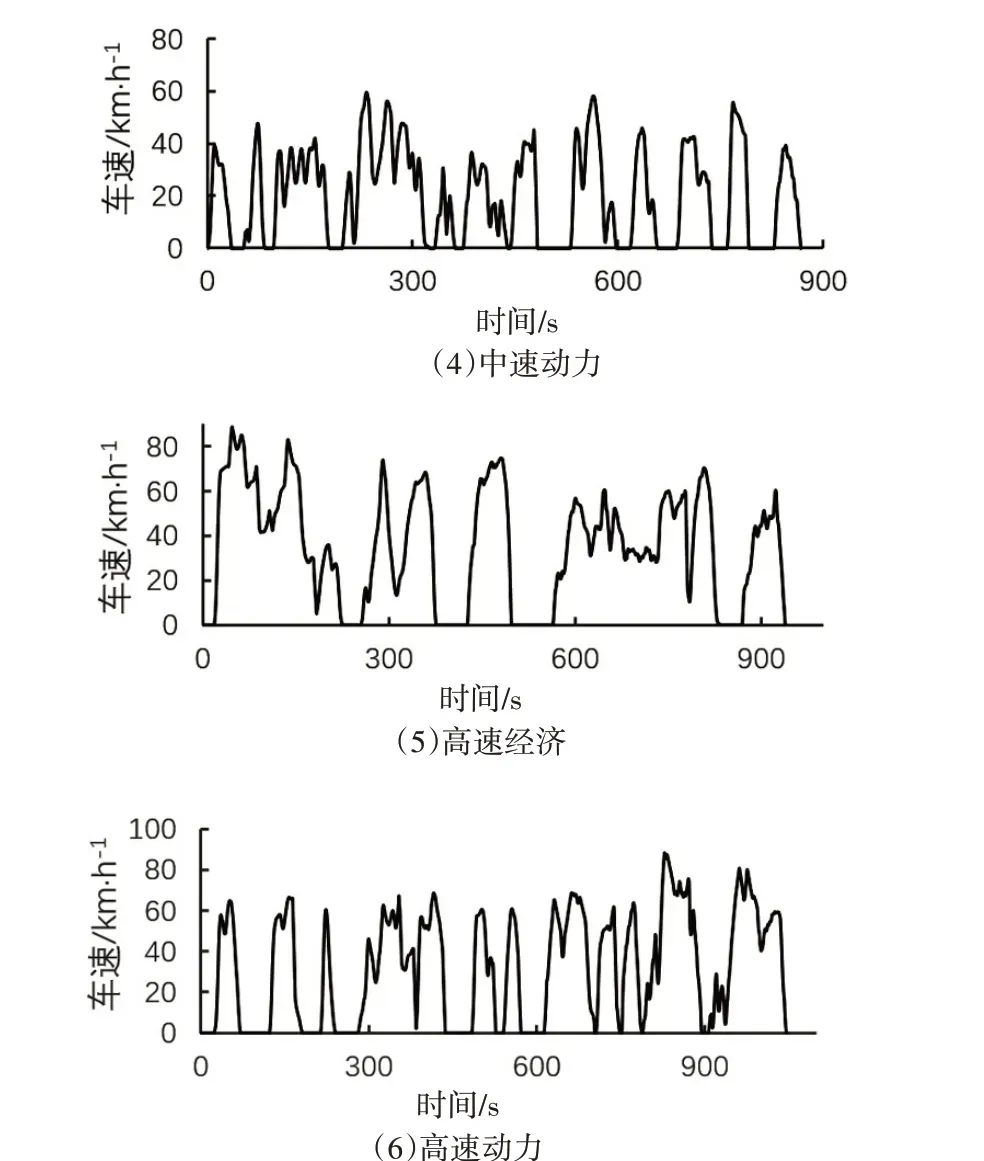
图2 合成后的典型工况

3.9 评价

由主成分载荷因子分析可知，平均车速、最大车速、车速标准差在新的主成分中的占比较大，因此，这通过计算这3 个行驶特征参数的累计平均误差（表10），以此误差来评价合成工况的结果。

表10 合成工况与源数据的特征累计误差

4 结束语

以优化目标投放城市的在研车型的经济性优化为目的，确定了长春市代表性工况设计的方案。

依据已有近16 000个运行片段的行驶工况数据，经过运动学片段的分类、主成分分析、聚类分析，共设计出6个长春市代表性工况，完成了对混动车辆动力总成模式的切换条件的优化，并形成了工况设计的自主积累。