基于改进熵权-未确知测度模型的城市污水深隧下穿既有铁路施工风险评价
2021-12-04张延军李胡爽侯伟涛董德雄田湖南
阮 超,张延军,李胡爽,侯伟涛,董德雄,田湖南
(1.中建三局绿色产业投资有限公司,湖北 武汉 430058;2.武汉威思顿环境系统有限公司,湖北 武汉 430073;3.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室,湖北 武汉 430071)
随着城市开发建设的迅速推进,污水处理厂等环境敏感污水设施与城市用地相互制约的问题日益突出,采用污水深隧技术外迁现有污水处理厂日益重要。相比于其他施工方法,例如明挖法和顶管法,盾构法可实现自动化作业,且不影响地面交通,有着无法比拟的优势。因此,目前污水深隧大多采用盾构法施工。然而,盾构隧道施工下穿既有运营铁路时极易诱发地层位移,造成轨道变形,严重影响列车运行和人民生命安全。因此,开展城市污水深隧下穿既有铁路施工风险评价具有重要的现实意义。
目前,已有不少学者针对该问题开展了针对性的研究。如Hyun等利用层次分析法讨论了盾构机掘进、选型风险;Rao等和Dai等对隧道施工风险展开了多级模糊综合评价;翟强等采用熵权法-层次分析法和未确知测度理论对隧道坍塌风险进行了评价;王永祥等对地铁施工的风险部位与风险因素进行了耦合分析,并将突变级数法应用于地铁盾构施工安全风险等级评价;黄萍等采用层次分析法建立动态事故树对管廊盾构施工风险进行了评价;巴振宁等基于模糊网络分析方法对市政排水管网运行的安全风险进行了评价。
然而上述研究大多是针对隧道结构本身进行的,而较少考虑隧道施工风险。在盾构隧道下穿既有铁路方面,目前的研究多以数值仿真为主,涉及的风险评估理论较少,且已有的风险评价方法在工程应用中仍存在一定的缺陷。如层次分析法、模糊综合评价法中各指标权重的确定是依赖于专家经验,采用最大隶属度原则取大运算时容易造成评价结果的失真。鉴于此,本文将未确知测度理论和信息熵理论相结合,用于城市污水深隧下穿既有铁路施工风险评价中。首先通过运用未确知测度理论来建立评价指标未确知测度函数;然后采用修正熵值法计算评价指标的客观权重,并将其耦合到评价指标的单指标测度评价向量中,构建基于改进熵权-未确知测度模型的城市污水深隧下穿既有铁路施工风险评价的多指标综合评价向量;最后利用置信度识别准则来判别施工风险等级,以弥补最大隶属度识别准则的不足。
1 改进熵权-未确知测度评价模型的建立
1.1 单指标测度评价向量的建立
设有n
个指标影响隧道施工,用X
={x
,x
,…,x
}表示评价对象,并且x
(i
=1,2,…,n
)表示其观测值。若x
有m
个风险等级,用P
(k
=1,2,…,m
)表示,记T
={P
,P
,…,P
)为评价空间。若第k
级比k
+1级风险等级“高”,记为P
>P
+1。如果P
>P
>…>P
,称{P
,P
,…,P
}是一有序分割类。若μ
=μ
(x
∈P
)表示x
隶属于P
的程度,并且符合下列要求:0≤μ
(x
∈P
)≤1(1)
μ
(x
∈T
)=1(2)

(3)
公式(1)为“非负有界性”,公式(2)为“归一性”,公式(3)为“可加性”。若μ
同时满足公式(1)~(3),则称之为未确知测度。令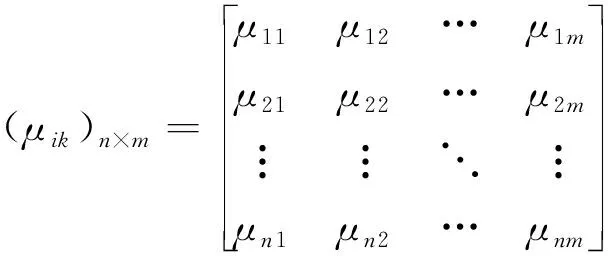
(4)
则公式(4)称为单指标测度评价矩阵,(μ
1,μ
2,…,μ
)则表示评价指标x
的隶属向量。由于线性型函数运算简单,使用广泛,因此本文采用线性型未确知测度函数来进行分析,见图1。
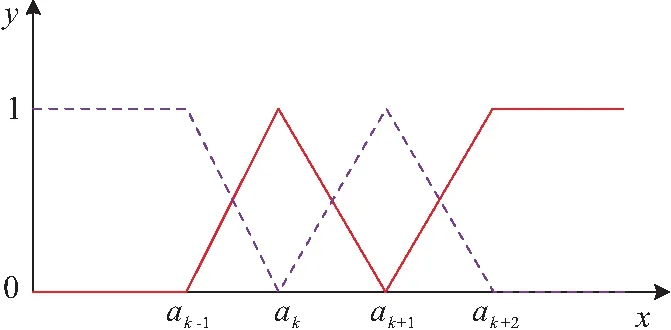
图1 线性型未确知测度函数图Fig.1 Function graph of the linear unascertained measurement
区间[a
,a
+1]表达式如下式所示: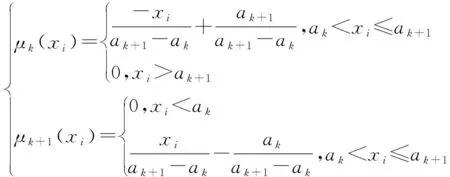
(5)
式中:a
和a
+1分别为第k
级和第k
+1级边界值,根据分类标准确定。1.2 改进熵值法确定评价指标的权重
考虑到目前评价指标权重的确定过于主观,本文引入信息熵理论,根据评价指标原数据信息来确定评价指标的权重,以尽可能消除主观因素的影响。具体熵的定义为:

(6)
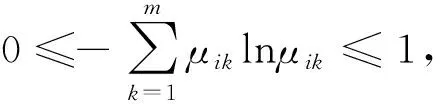
H
≤1。当μ
=0时,lnμ
无意义。因此,参考文献[15],本文将其修正为
(7)
该修正公式解决了传统公式的局限,并对熵值H
的影响较小。由于熵越大,权重越小,因此各指标权重w
可由下式计算得到: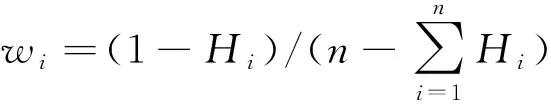
(8)

1. 3 多指标综合测度评价向量的确定
将计算得到的指标权重w
与单指标测度评价向量μ
进行耦合,若μ
=μ
(P
∈T
)表示待评价对象X
属于P
的程度,则有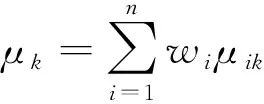
(9)

1. 4 置信度识别准则判定风险等级
当多指标综合测度评价向量(μ
,μ
,…,μ
)各等级所属隶属度较接近时,利用最大隶属度原则取大运算来确定最终风险等级,会出现分级不清、结果不合理等问题。例如模糊综合评价集E=(0.360,0.322,0.455,0.455,0.388),根据最大隶属度原则,评价结果同时属于Ⅲ级和Ⅳ级。因此,当存在隶属度相等情况时,仍采用最大隶属度原则进行分析,会出现无法判断的情况。因此本文引入置信度识别准则来确定隧道下穿既有铁路施工风险等级。设λ
为置信度,λ
取值范围为0.
5≤λ
<1.
0,λ
值越大,结果越保守。若P
>P
>…>P
,且令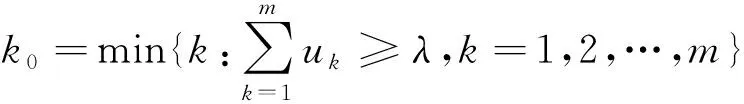
(10)
则认为评价对象X
属于第k
个评价等级P
。2 评价指标体系的建立及风险评估流程
2.1 城市污水深隧下穿既有铁路施工风险评价指标体系的建立
实际工程中,污水隧道施工风险影响因素较多,但总体来说,主要包括既有铁路运营风险因素、隧道盾构掘进控制风险因素、地质环境因素和勘察设计因素等。参考已有研究成果,选取铁路路基沉降X
、轨道差异沉降X
、铁路附属设施变形X
、土仓压力控制X
、掘进速度控制X
、盾尾注浆控制X
、地下水状况[隧道每10 m的进水量(L/min)]X
、隧道围岩等级X
、既有铁路等级X
、隧道埋深X
、地质勘察准确程度X
和盾构机选型X
12项因素作为未确知测度模型评价指标。其中,铁路附属设施变形X
、土仓压力控制X
、掘进速度控制X
、盾尾注浆控制X
、隧道围岩等级X
、既有铁路等级X
和盾构机选型X
为定性因素,采用半定量的方法进行取值;铁路路基沉降X
、轨道差异沉降X
、地下水状况X
、隧道埋深X
和地质勘察准确程度X
为定量指标,采用实测值进行评价。根据隧道施工风险特征,将评价空间T
={P
,P
,…,P
}定义为{P
,P
,P
,P
,P
},即Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ级,分别表示无风险(Ⅰ)、低风险(Ⅱ)、中等风险(Ⅲ)、高风险(Ⅳ)和极高风险(Ⅴ)。风险影响因素具体分级标准及赋值情况,见表1。
表1 城市污水深隧下穿既有铁路施工风险因素分级标准及赋值Table 1 Classification standards of construction risk factors and the assigned values of urban wastewater deep-buried tunnels under-passing existing railway
2.2 风险评估流程
采用基于改进熵权-未确知测度模型进行城市污水深隧下穿既有铁路施工风险评价技术线路如图2所示,具体步骤为:
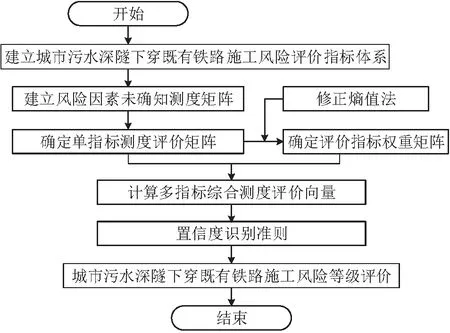
图2 基于改进熵权-未确知测度理论模型的城市污水 深隧下穿既有铁路施工风险评价流程Fig.2 Construction risk assessment process of urban wastewater deep-buried tunnels under-passing existing railway based on the improved entropy weight-unascertained measurement theory
(1) 确定风险影响因素和分级标准;
(2) 利用公式(5)建立单指标未确知测度函数;
(3) 确定单指标测度评价矩阵;
(4) 根据公式(6)~(8),运用信息熵理论确定指标客观权重;
(5) 根据公式(9)计算多指标综合测度评价向量;
(6) 根据公式(10),利用置信度识别准则对隧道施工风险进行评价。
3 实例应用
3.1 工程概况
武汉大东湖核心区污水传输系统工程将位于武汉市中心城区的污水传输至新建北湖污水处理厂集中处理。该项目设计规模近期为80万t/d,远期为150万t/d,武汉市近三分之一的污水将经过这条深隧进行预处理,近期服务范围包括大东湖核心区内约130.35 km,远期服务范围约200.25 km,服务人口预计达到300万。主要建设内容包括新建17.5 km的主隧及1.7 km的支隧、污水深隧系统与地表的沙湖污水提升泵站、二郎庙预处理站、落步嘴预处理站、武东预处理站等,建成以后将有效保护城市中心湖泊和港渠,提升大东湖核心区水环境水质,如图3所示。本文主要对盾构污水隧道下穿武广高铁段的风险进行分析,穿越段的节点断面如图4所示。

图3 大东湖污水深隧全景透视图Fig.3 Panoramic perspective of Great East Lake wastewater deep-buried tunnel
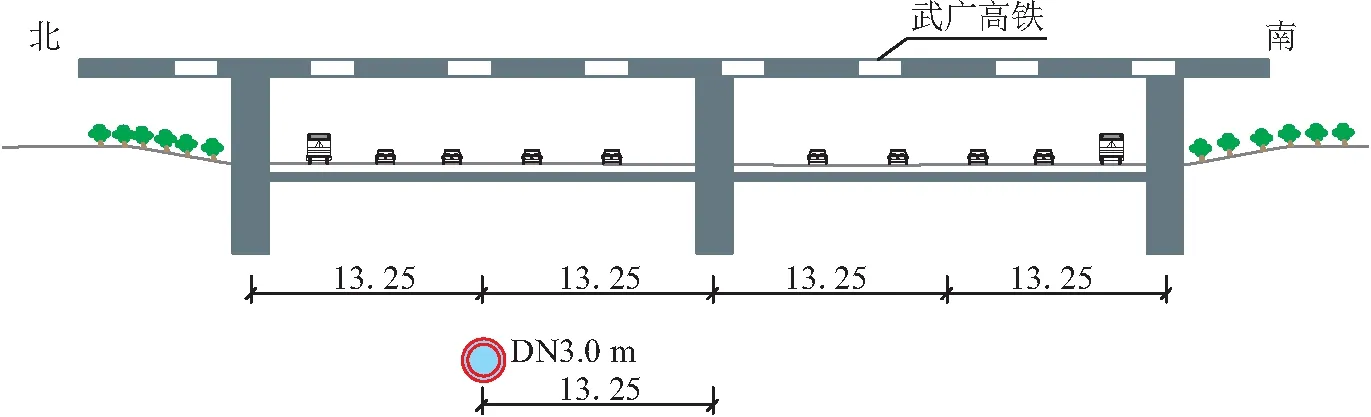
图4 大东湖污水深隧下穿武广高铁节点断面示意图(单位:m)Fig.4 Section diagram of the joint of Great East Lake wastewater deep-buried tunnel under-crossing Wuhan—Guangzhou high-speed railway (unit:m)
通过对该段工程地质、水文地质进行整理分析,并结合现场施工组织设计情况,得到污水隧道下穿段各影响因素参数和等级,见表2。

表2 大东湖污水深隧下穿武广高铁段的风险因素特征及其风险等级Table 2 Risk factors and risk levels of Great East Lake wastewater deep-buried tunnel under-crossing Wuhan—Guangzhou high-speed railway
3.2 构建单指标未确知测度函数
根据函数定义,结合表1中各评价指标的测度值,得到各评价指标的未确知测度函数图,见图5。其中,铁路路基沉降X
、轨道差异沉降X
、地下水状况X
、隧道埋深X
和地质勘察准确程度X
的单指标测度函数分别见图5(a)~5(e);铁路附属设施变形X
、土仓压力控制X
、掘进速度控制X
、盾尾注浆控制X
、隧道围岩等级X
、既有铁路等级X
和盾构机选型X
的单指标测度函数见图5(f)。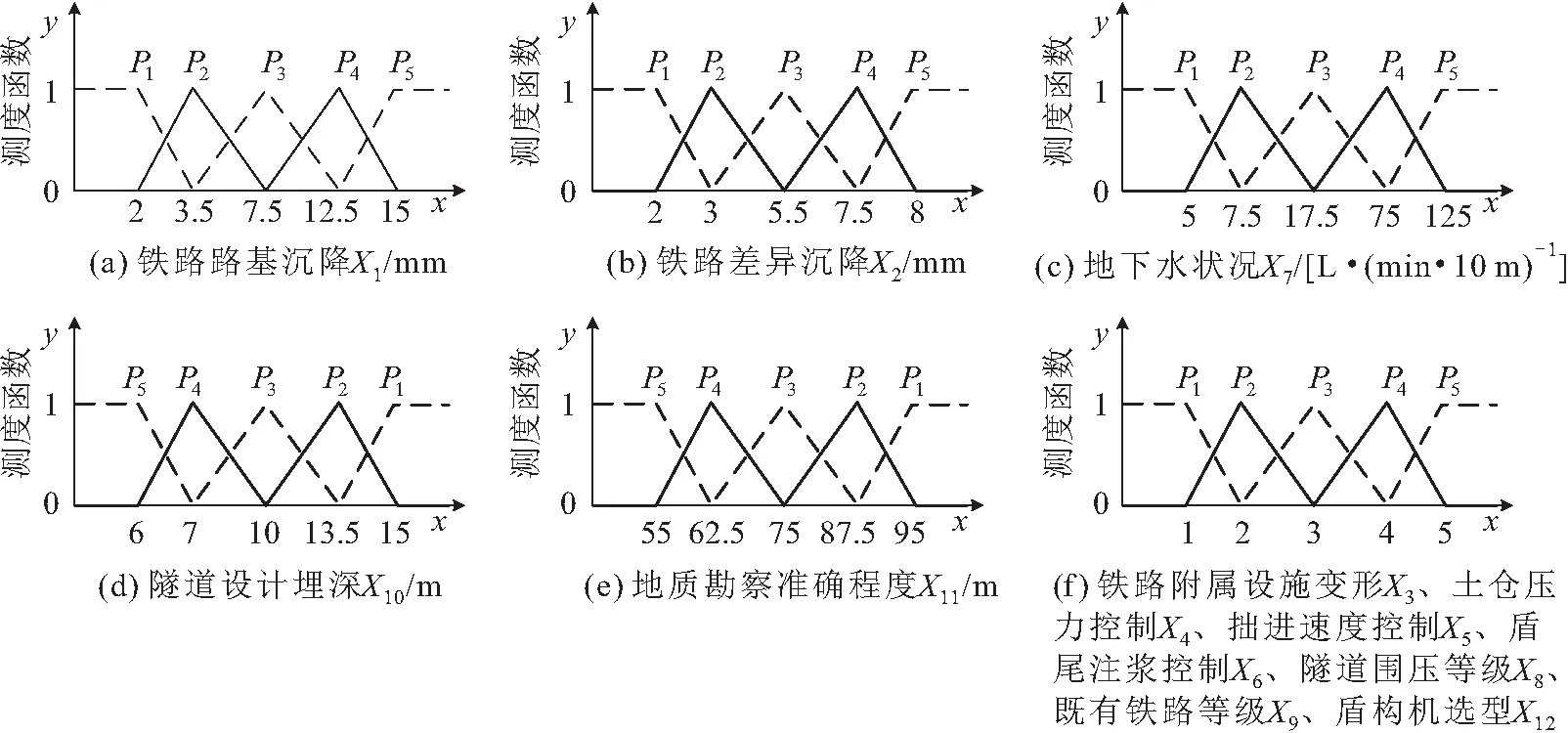
图5 大东湖污水深隧下穿武广高铁施工风险评价指标未确知测度函数图Fig.5 Unascertained measurement function graph of evaluation indices for construction risk of Great East Lake wastewater deep-buried tunnel under-crossing Wuhan—Guangzhou high-speed railway
根据表2中各评价指标的特征,结合图5中各评价指标的未确知测度函数图,可以求得大东湖污水深隧盾构下穿既有武广高铁里程K6+260~K6+280段的单指标测度评价矩阵为

3.3 计算多指标综合测度评价向量
将各评价指标对应的数据代入公式(6)~(8),得到各评价指标的权重为:w
=0.
090 59,w
=0.
051 56,w
=0.
090 59,w
=0.
090 59,w
=0.
090 59,w
=0.
090 59,w
=0.
064 58,w
=0.
090 59,w
=0.
090 59,w
=0.
090 59,w
=0.
068 55,w
=0.
090 59。然后,利用公式(9)求得多指标综合测度评价向量为=[0.362,0.226,0.256,0.009,0.147]3.4 置信度识别
考虑到城市污水深隧施工风险造成的影响巨大,本文取置信度λ
=0.
7,结合公式(10)置信度识别准则来确定该工程的施工风险等级。当k
=2时, 0.
362+0.
226=0.
588<λ
=0.
7;当k
=3时, 0.
362+0.
226+0.
256=0.
844>λ
=0.
7。因此,可以判定大东湖深隧盾构下穿既有武广高铁里程K6+260~K6+280段风险等级为Ⅲ级(中等风险)。3.5 结果分析
在当前施工组织设计情况下,现场隧道盾构下穿武广高铁段,实际监测数据正常,施工未见异常,安全通过(如图6所示),施工实际风险等级较低,与采用未确知测度模型预测的结果基本一致。可见,将该理论应用于城市污水深隧下穿既有铁路施工风险评价是可行的。

图6 大东湖污水深隧盾构下穿武广高铁段施工状况Fig.6 Construction status of Great East Lake wastewater deep-buried shield tunnel under-passing Wuhan—Guangzhou high-speed railway
4 结 论
(1) 将未确知测度理论应用于城市污水深隧下穿既有铁路施工风险分析中,并建立了施工风险评价的未确知测度模型。利用置信度识别准则来判别最终施工风险等级,较好地解决了城市污水深隧下穿既有铁路风险等级评价中多指标性、模糊性和不确定性等问题。
(2) 在风险评价中,将信息熵理论和未确知测度理论进行耦合,根据评价对象原数据信息利用熵权来确定评价指标权重,减少了人为因素的影响,提高了评价结果的可靠性。
(3) 将本文方法应用于大东湖污水深隧下穿武广高铁段的施工风险评价中,评价结果与实际情况基本吻合,为城市污水深隧下穿既有铁路施工风险评价提供了新思路。
