基于板料机械性能参数的FLC快速计算方法
2021-12-03孙明东董景文陈伟华冯国卫刘益成孙胜伟
孙明东,董景文,陈伟华,冯国卫,刘益成,孙胜伟
(一汽—大众汽车有限公司 青岛分公司,山东 青岛 266000;一汽—大众汽车有限公司,吉林 长春 130000)
0 引言
随着汽车产业的发展,对汽车车身冲压件的质量要求越来越高。影响零件质量的因素是多方面的,板料成型性能是影响冲压件质量的关键因素。材料成型极限曲线(FLC)作为汽车冲压件成型模拟或网格实验的重要判断依据,在汽车快节奏研发、模具的快速调试以及快速解决大批量生产过程中的拉裂、颈缩等问题中起关键性作用。更为真实的FLC可通过实验获得[1],但是实验试样加工时间长、实验周期长,应用在工业生产中的效率不高。
长期以来,不少学者对基于塑性理论[2]和有限元仿真[3]的成型极限预测进行了研究。但在生产中的汽车冲压件成型模拟或网格实验中,应用比较广的仍为Keeler和Brazier[4]提出的经验公式(以下简称Keeler公式),通过板料的厚度和加工硬化指数计算获得。
Keeler公式通过采集大量不同板材不同变形区域的数据而得到的经验公式,可在大范围的FLC预测中使用。然而,汽车车身冲压件板料性能相对集中,尤其是外表面件的材料基本以DC04、 DC06为主,利用经验公式获得的FLC曲线仍然和实验数据存在不小差异,因此,如何快速准确得到实际生产的板料的FLC曲线仍是汽车冲压生产中需要研究的课题。
本文针对整车厂汽车车身冲压件板料,通过单向拉伸实验机测得板料的机械性能参数,并且利用杯突实验机测得FLC,进行小范围数据的计算,得到了更精确的预测结果。
1 实验设备及材料
1.1 FLC测量实验设备
线切割机、杯突实验机和Aramis光学全场动态应变测量仪等。
1.2 板料机械性能参数测量设备
采用Zwick/Roell单向拉伸实验机。
1.3 材料
本研究选用9种现生产的汽车外表面覆盖件板料,主要为DC04、 DC06深冲钢。
2 实验过程及结果
2.1 实测FLC
(1) 用线切割机将板制作成试样[1]。每条曲线选8种形状。每种材料每种形状各选3片。
(2) 板料喷散斑后用杯突实验机做实验,同时用Aramis光学全场动态应变测量仪记录数据,如图1所示。

(a) 杯突实验

(b) 光学应变测量分析图1 杯突实验应变测量分析
(3) 数据处理。每种形状3片材料的数据取平均值,生成asc文件及FLC曲线。
2.2 板料机械性能参数
(1) 单向拉伸实验,如图2所示。

图2 板料拉伸实验
(2) 生成板料单向拉伸机械性能参数,如表1所示。
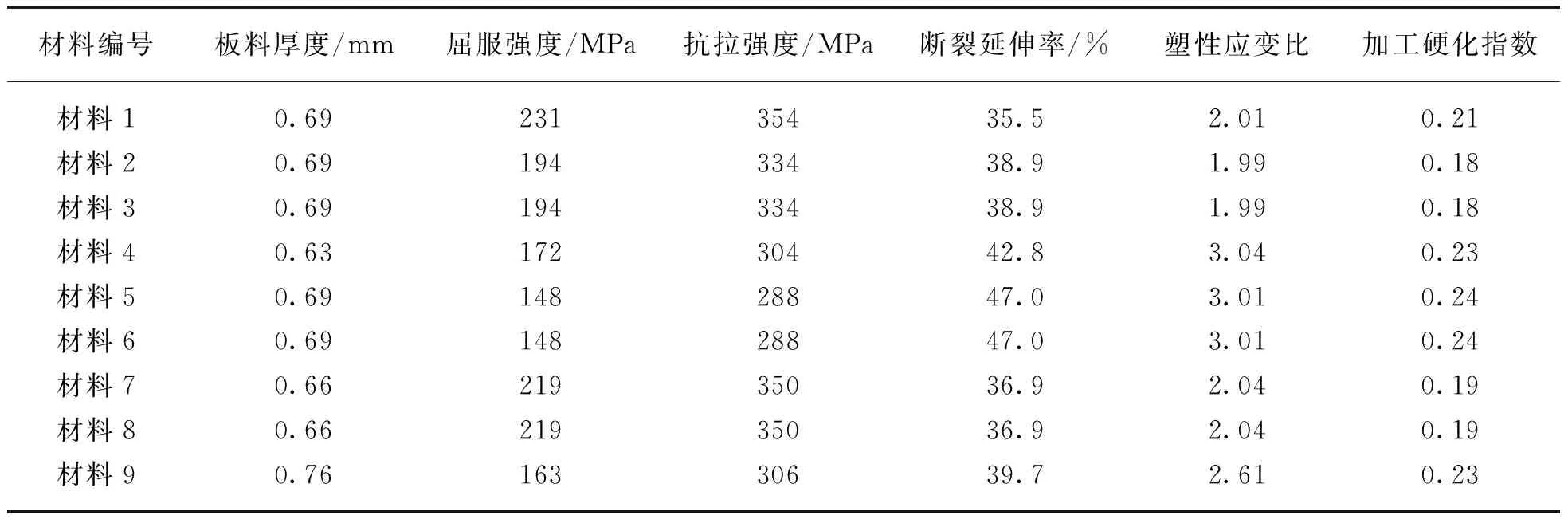
表1 不同板料机械性能参数
2.3 测试结果
测量FLC结果如图3所示。不同型号钢板测量所得FLC整体趋势一致,但在最左侧拉压状态变形和最右侧双向拉伸变形主次应变均有较大差异。
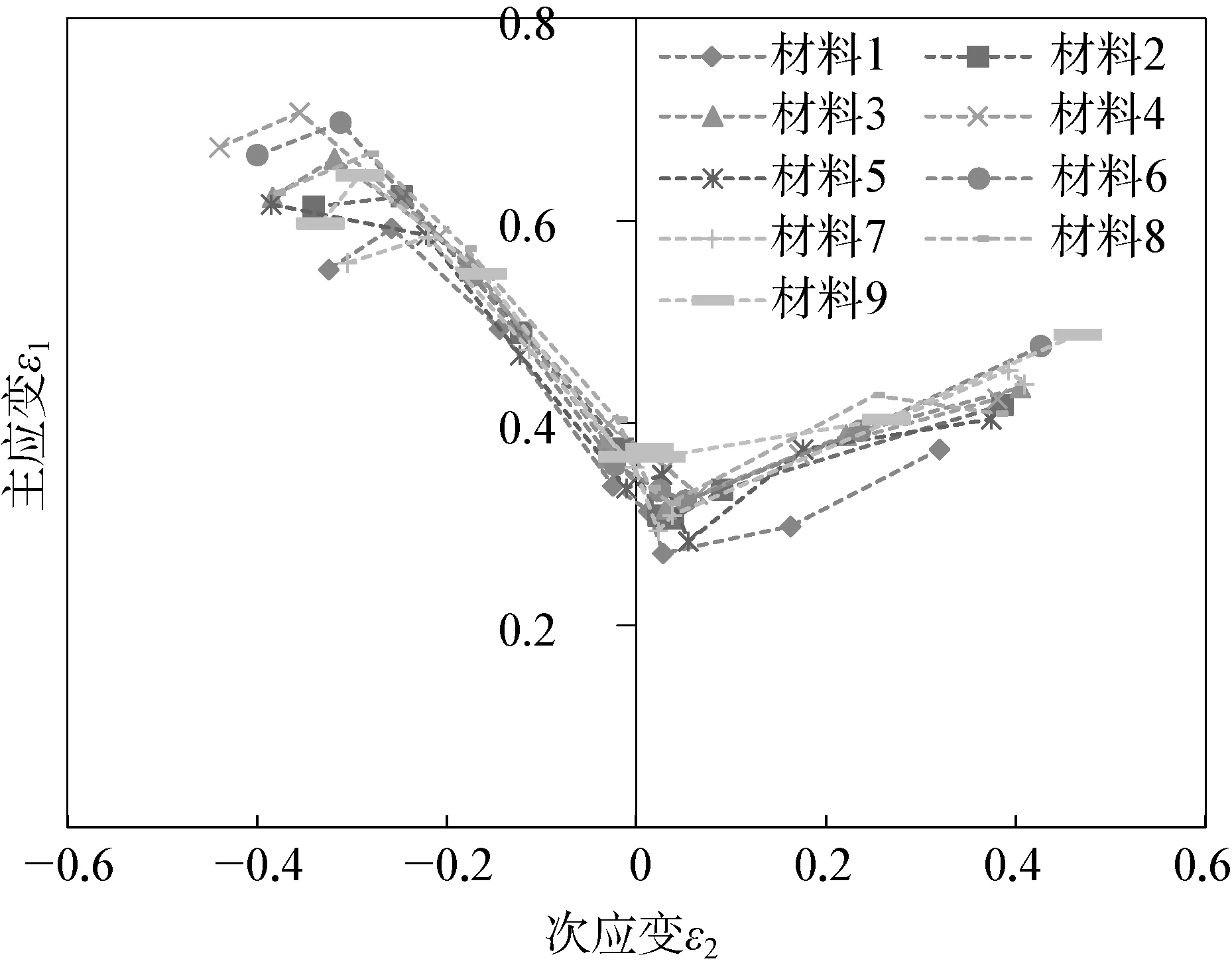
图3 不同汽车钢板测量所得FLC曲线
3 数据分析
采用回归分析的方法研究机械性能参数对FLC的影响。选择机械性能参数厚度a0、屈服强度Rp、抗拉强度Rm、延伸率A、塑性应变比r、应变硬化指数n为自变量,板料的单向拉伸状态临界应变为因变量。建立FLC关于机械性能参数的回归模型:
ε=f(a0,Rp,Rm,A,r,n)+Δ,
(1)
3.1 参数选择
对实验测量的数据进行因子分析,如图4所示。在3个公共因子空间数据图中,可分为3个区域,其中,屈服强度和抗拉强度各自分别在一区域,而板料厚度、延伸率、塑性应变比、应变硬化指数与FLC在同一区域,因此说明屈服强度和抗拉强度与FLC公共因子较少,关联性不强。公共因子个数为3个,累积贡献率为86.3%。因此在后序计算中将考虑板料厚度、延伸率、塑性应变比、应变硬化指数4个参数。
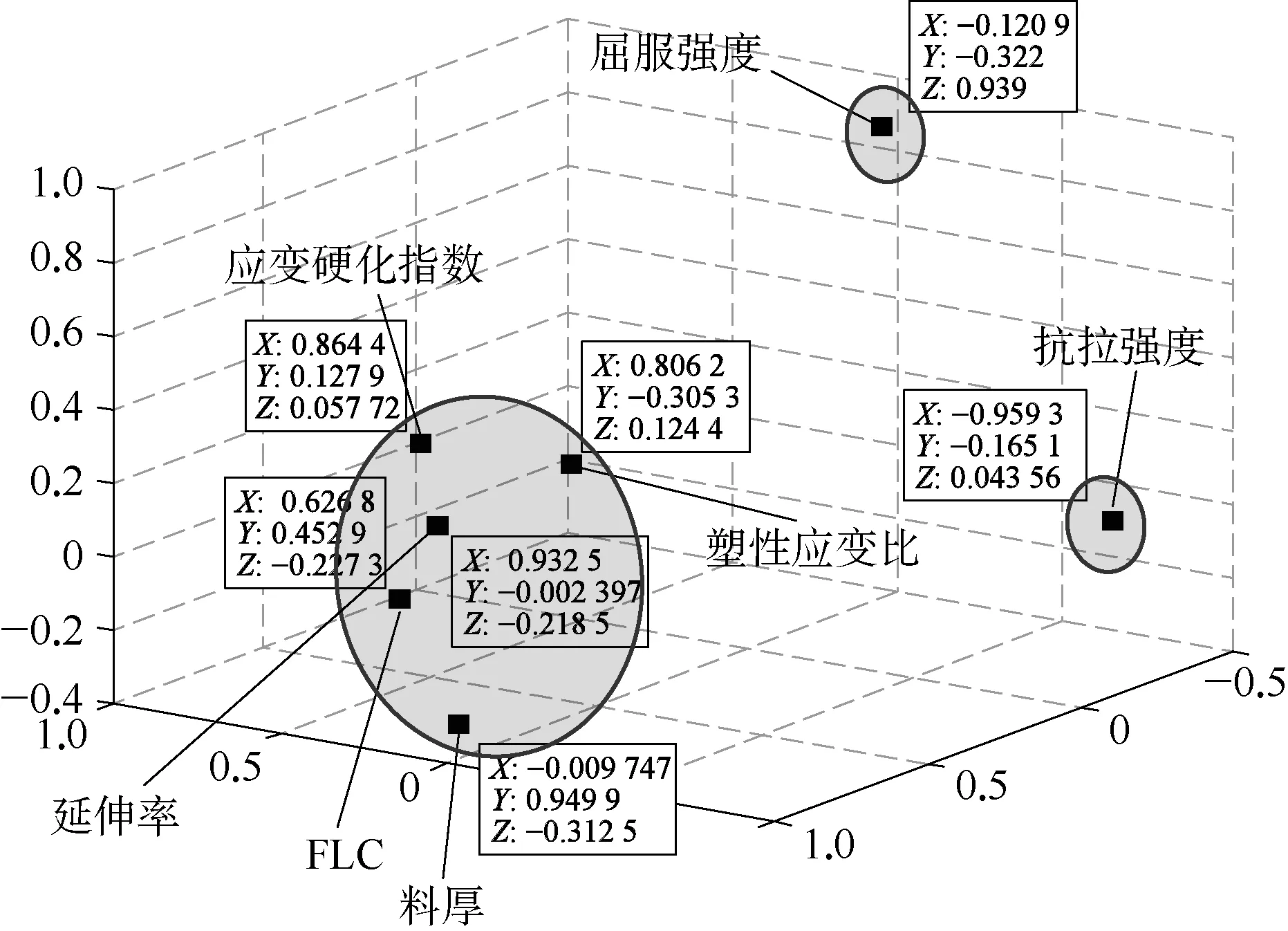
图4 因子分析结果
3.2 回归模型的建立
根据因子分析,剔除屈服强度和抗拉强度。根据Keeler等[4]的研究,考虑a0与n的交叉影响,建立线性回归方程:
ε=a+b·a0+c·A+d·r+e·n+f·a0·n
(2)
选用式(2)回归模型对8种试样主次应变分别进行回归分析,可得到各应变回归方程系数矩阵(见表2)。
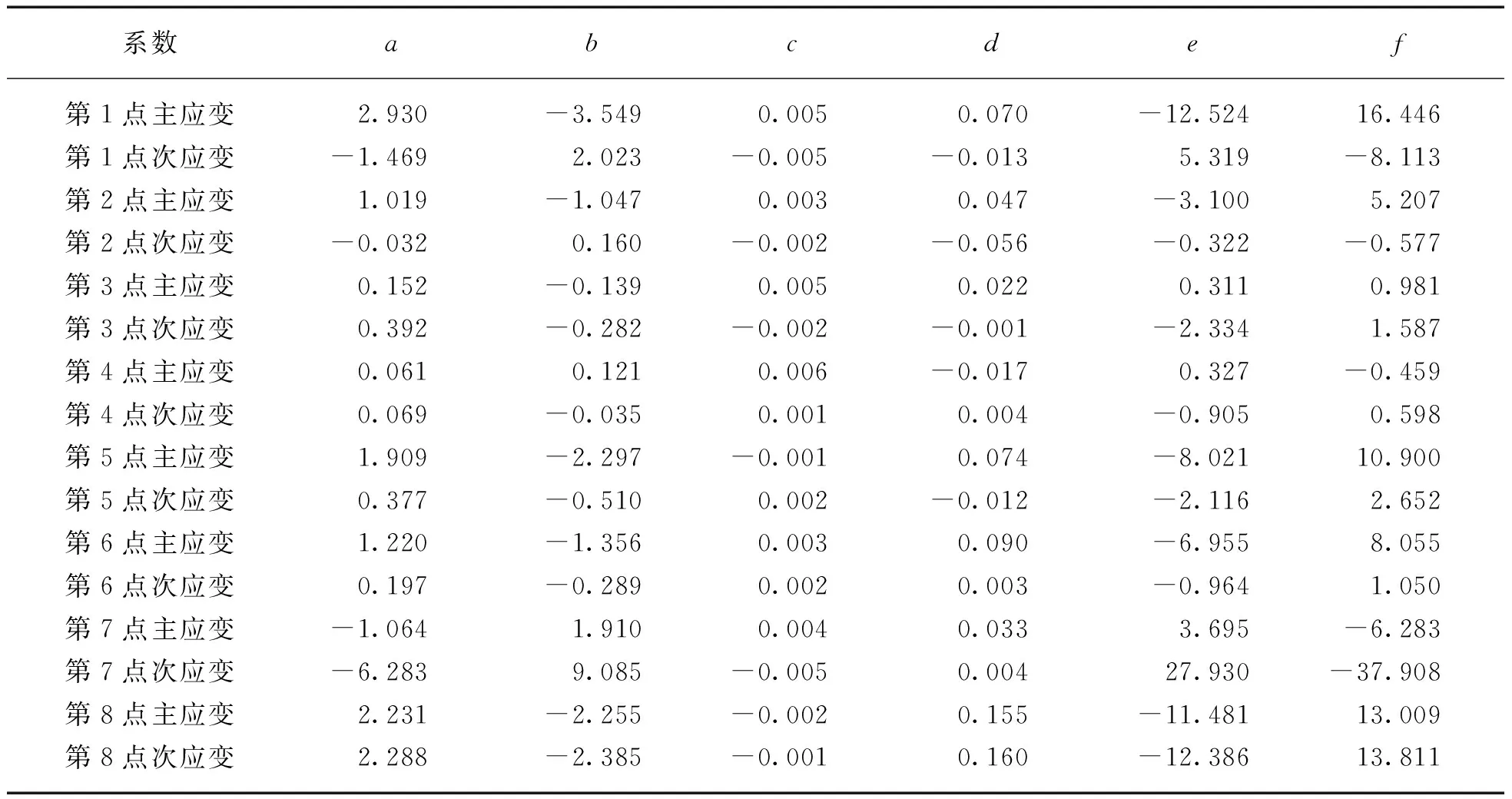
表2 回归方程系数矩阵
4 预测回归模型效果
整条曲线公式为:
(3)
其中,ε2为次应变;
ε1为主应变;
FLC0为次应变为0时的主应变值;
t为板料厚度;
n为应变硬化指数。
将预测回归模型FLC与实际测量FLC、 Keeler公式[含有些研究[5]中的整条曲线公式,如公式(3)]计算FLC进行比较,以部分零件板料为例,得出对比图,如图5所示。
由图5可知: 本研究所选用的预测回归模型,对FLC实测值的拟合效果较好。拟合曲线与用Keeler公式得到的FLC曲线趋势是一致的,单向拉伸最低点比较接近,拉压状态和双向拉伸状态下拟合曲线值比Keeler公式值较低,更符合实际情况,使用预测回归模型得到的FLC曲线安全性更高。

图5 某车型前盖外板FLC
5 结论
本文以主、次应变为因变量,板料机械性能参数为自变量建立了汽车冲压件板料的预测回归模型,在考虑机械性能参数交叉影响时的拟合效果更好。通过建立有交叉影响的参数回归模型,降低了自变量的维度,得到预测回归模型。
计算出预测回归模型系数矩阵,预测回归模型拟合优度指标较高,拟合效果较好。将预测回归模型FLC曲线与Keeler公式FLC曲线对比可知: 三者趋势一致,本模型的单向拉伸最低点比较接近,拉压状态和双向拉伸状态预测回归模型值略低,安全性更高。
该模型为钣金冲压成型提供了参考。同时,该方法为小范围内FLC模型的计算提供了思路,即通过内部测量数据,利用因子分析,查找出相关联因素,然后通过数据回归方法预测的模型往往比通用的常规模型更精确,为企业内部应用提供了个性化服务。
