基于剩余熵黏度标度理论预测混合制冷工质黏度

康凯,谷雅秀,王晓坡

(1.长安大学建筑工程学院,710061,西安;2.西安交通大学热流科学与工程教育部重点实验室,710049,西安)

准确描述制冷工质的黏度性质有利于降低制冷系统内部压降从而改善换热效率,对工业过程设计、系统优化以及设备研发有重要意义[1]。此外,液相系统具有较短的分子平均自由程,导致其中存在很强的分子间相互作用,而探究其黏度性质有助于理解分子间作用中潜藏的客观规律和内在机理[2]。

Mclinden等研究表明,现有单一工质难以兼顾实际生产对替代工质热力学性能的需求与日益严苛的安全及环保法规[3]。而选取适当的配比能够使混合工质保留各组分的优点,这样既可以缓解使用制冷工质对全球变暖的不利影响,又能保障使用时的安全性,并大幅度降低因循环工质更替而导致的更换系统装置所造成的经济损失。因此,如何构建性能优良的潜在多元混合制冷工质是当前研究的重点问题。随着各种新型环保混合制冷工质的不断提出,其黏度数据是必须首先解决的关键基础问题之一。由于完全依靠实验测试不可能获得任意配比和工况下的混合制冷工质黏度性质,因此通常采用准确可靠的黏度模型进行有效补充。Rosenfeld提出的剩余熵标度规律能够将流体无量纲黏度和剩余熵间建立明确的函数关系[1],而扰动链统计缔合流体理论(PC-SAFT)是近年来得到广泛应用的一种模型参数具备明确物理内涵的热力学状态方程[4]。Novak于2011年将上述两种理论相结合,以18种烷烃为研究对象提出了基于PC-SAFT链节参数的剩余熵黏度标度理论[5]。在其研究基础上,Lötgering-Lin和Fouad等人基于基团贡献法极性版PC-SAFT状态方程(即GC-Polar PC-SAFT)改进了对比无量纲黏度与剩余熵间的函数关系,并成功推广到5种氢氟烃(HFC)和2种氢氟烯烃(HFO)类制冷工质[6-7],证明了该理论在一定程度上具备准确描述制冷工质系统黏度性质的潜力。

近两年来,基于剩余熵标度方法对混合制冷工质的理论研究已逐渐成为国内外的研究热点。热力学状态方程是剩余熵标度方法中计算系统剩余熵和相平衡性质的理论基础,如何在回归尽量少的模型参数的前提下同时兼顾其计算精度对于黏度模型的工程应用尤为重要。基于此,Liu等人利用CPA状态方程对部分二元HFC/HFO混合系统的气、液相黏度性质开展了开拓性研究,引入缩放因子简化了现有剩余熵标度方法工程应用的难度[7]。Yang等人基于Liu的研究构想[8],进一步通过多参数Helmholtz能状态方程给出的系统剩余熵提出了一套能够准确描述混合系统的关联函数,并与广义对应态模型进行全面的比对并阐述其优势和不足[9]。简化版PC-SAFT(sPC-SAFT)[9]和CPA相较于Polar PC-SAFT和多参数Helmholtz能状态方程模型参数更少,对于非缔合物质,前两种模型参数均为3个,这对于实验数据较为匮乏的物质来说有利于减少参数回归时必需的实验数据量,一定程度上降低了剩余熵标度方法在工程实际中推广和使用的难度。但与CPA相比,sPC-SAFT对于系统基础热力学性质(如液相密度性质)的预测更为准确[10],可为剩余熵标度方法提供坚实的理论支撑。

基于兼顾模型计算精度和模型参数数量的考量,本文选取Novak提出的基于链节参数的剩余熵黏度标度理论,利用计算效率更高的sPC-SAFT状态方程,对11种制冷工质(包括HFO、HFC、烷烃和CO2)的黏度性质进行了计算,同时结合预测性无量纲对比黏度混合法则,将该理论推广至更多元、更复杂的混合系统。通过与文献实验数据进行比对,验证该理论在三元等更多组分复杂系统内的有效性和实用性,评估其优势和局限性,可为进一步推动新型环保混合工质的工程应用提供理论依据和基础数据。

1 理论模型

1.1 简化版PC-SAFT状态方程

基于统计缔合理论的PC-SAFT方程是由Gross等在扰动理论的基础上,以硬球链为参考系统提出的[4]。基于剩余Helmholtz自由能的PC-SAFT状态方程如下

ares=ahc+adisp+aass

(1)

式中:ahc、adisp和aass分别是硬链参考项、色散力以及缔合作用(如氢键)的贡献项。对于非缔合流体,PC-SAFT具有3个包含明确物理意义的模型参数,即链节数m、各链节的硬球直径σ和各链节的能量参数ε/kB。PC-SAFT模型参数通常由纯质饱和蒸汽压及液相密度实验数据回归得到。von Solms在原始版本PC-SAFT的基础上对其混合法则进行优化,从而获得了一种能够保证计算精度同时提高计算效率的数学模型,即sPC-SAFT。鉴于sPC-SAFT仅改进了模型混合法则,因此其与PC-SAFT状态方程的纯质模型参数完全一致。

结合公式(1),特定工况下的系统剩余熵可通过系统剩余Helmholtz自由能对温度的偏导计算得到,即

(2)

式中:ρ、T、R和Sres(ρ,T)分别表示密度、温度、理想气体常数和系统剩余熵。

1.2 剩余熵黏度标度理论

在Rosenfeld的研究成果中,他系统阐述了简单流体的无量纲对比黏度(η*)能够通过系统剩余熵估算得到[1],具体的计算公式如下

(3)

式中:Ai和Bi是与工质对应的标度参数;NA和kB分别表示阿伏伽德罗常数和玻尔兹曼常数。但是该模型在低密度区的黏度预测能力有限,尤其是无法准确描述具有长程极性作用或者短程氢键系统的黏度性质。基于此,Novak采用Chapman-Enskog黏度(ηCE,i)得到了更准确的纯质无量纲对比黏度计算公式[5],即

(4)

式中

(5)

(6)

式中:mi为组分i的链节数;Ci、Di均为无量纲黏度系数;

(7)

对于复杂混合系统,本文在Fouad和Vega的工作基础上,利用sPC-SAFT状态方程,并采用Lötgering-Lin所提出的无量纲对比黏度混合法则[11]以及Wilke提出的Chapman-Engskog黏度混合法则[6]进行计算,其无量纲对比黏度所采用的混合法则为

(8)

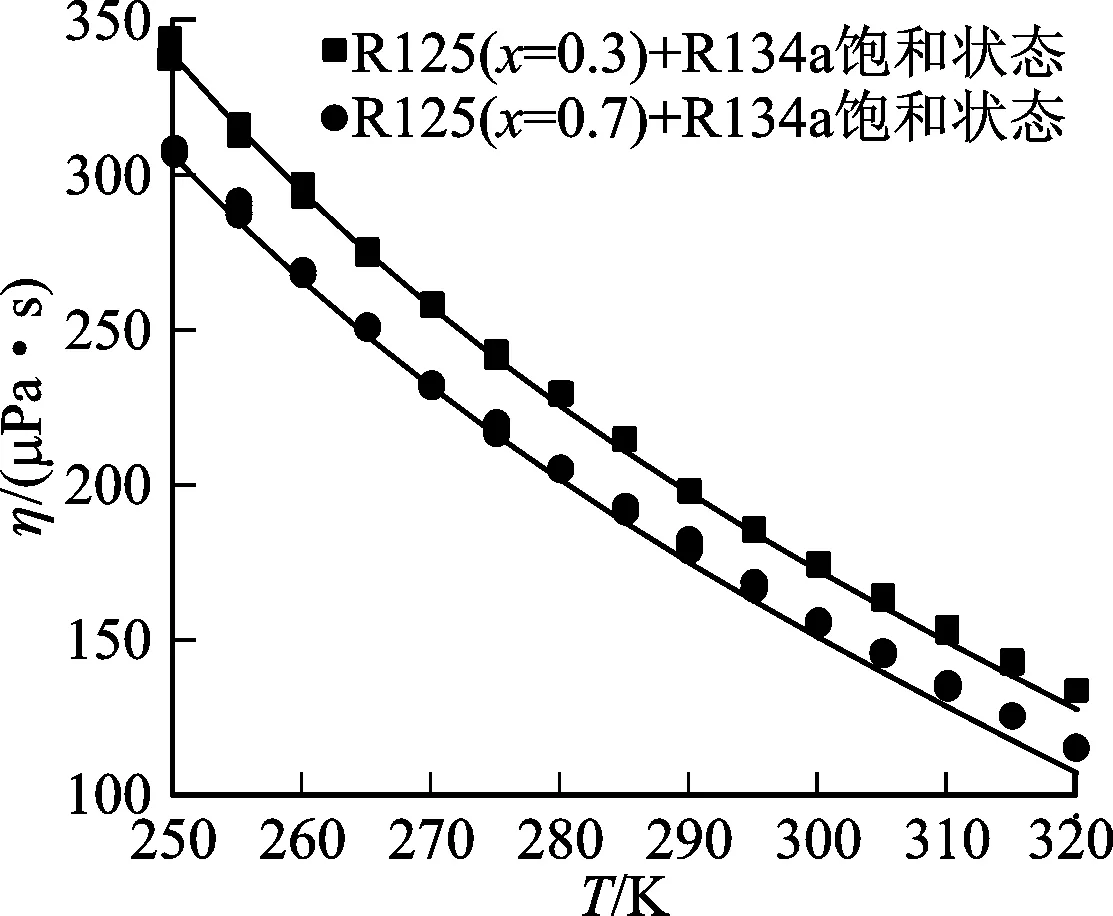
Wilke提出的Chapman-Engskog黏度估算混合法则[5]如下

(9)

式中

(10)

2 模型计算结果与讨论

2.1 无量纲对比黏度多项式参数和二元作用参数

本文首先对文献中目标工质的PC-SAFT模型参数进行整理搜集,并自行回归得到R134a、R32、R125和R143a的模型参数,详见表1,表中Dρ为本文计算值与文献饱和液相密度的平均绝对偏差。

(11)

式中:N为实验数据个数;ηi,cal、ηi,lit分别为黏度计算值和文献值。

结合表1中的模型参数,利用PC-SAFT状态方程导出剩余熵,然后采用NIST数据库[12]给出的纯质饱和液相黏度数据建立对数无量纲对比黏度与剩余熵的关联式,参照式(6)。所得无量纲多项式参数(A、B、C、D)和相应温度范围详见表2,Dη为文献黏度值与计算值的平均绝对偏差。

表1 目标工质的PC-SAFT模型参数

为了验证表2中参数的可靠性,系统比对了剩余熵黏度标度理论计算值与文献中目标纯质黏度实验数据。对于本文所研究的纯质系统,剩余熵黏度标度理论在不同工况下的计算结果准确,最大绝对平均偏差小于4.36%。图1中实线为R1234yf和R1234ze(E)黏度计算值,可以看出,计算值与文献黏度实验数据吻合良好。

(a)R1234yf[13]

表2 目标工质对比黏度标定参数

此外,鉴于研究对象属于复杂多元混合制冷工质体系,其中可能存在受分子结构及静电分布影响的高度非理想黏度性质,为了更好地描述系统不同工况,特别是饱和状态下的剩余熵性质,本文首先系统研究了目标工质的二元汽液相平衡性质及对应的二元作用参数。

图2给出了R152a+R600a和R32+R134a的等温汽液相平衡性质比对结果。符号和实线分别表示文献黏度实验数据和本文计算结果。实验数据与本文计算值间的最大绝对平均偏差小于1.3%。根据结果可以看出,sPC-SAFT状态方程能够准确预测包括共沸或近共沸(如R152a+R600a)以及接近理想溶液性质(如R32+R134a)的二元体系汽液相平衡性质,为剩余熵黏度标度理论提供了坚实的理论支撑。表3给出基于文献数据得到的二元作用参数。

(a)R152a+R600a[16]

表3 基于汽液相平衡性质的二元作用参数kij回归值

2.2 多元混合制冷工质体系黏度预测

在纯质黏度计算结果和kij的基础上,结合无量纲对比黏度混合法则,本文计算得到多元体系基于链节的剩余熵黏度标度理论的计算值并与文献实验数据进行系统比对。图3给出了部分混合工质不同温度压力工况下的黏度计算值(实线)与表示文献黏度实验数据(符号)比对结果,图中x为摩尔分数。从图3可以看出,剩余熵黏度标度理论适用于目标混合工质系统,能够准确预测二元及以上多元系统饱和状态下及高压工况下不同温度的液相黏度性质。此外,多元制冷工质体系(如图3d和图3e)实验数据中存在部分无可用二元作用参数的工质对(如R32+R125、R32+CO2和R1234yf+CO2等)。剩余熵黏度标度理论能准确地反映其黏度性质,验证了基于链节的剩余熵黏度标度理论在三元及以上复杂混合工质系统的预测能力,同时也从侧面说明该理论具备明确的物理内涵,具有较强的预测复杂系统黏度性质的能力以及较高的工程应用价值。

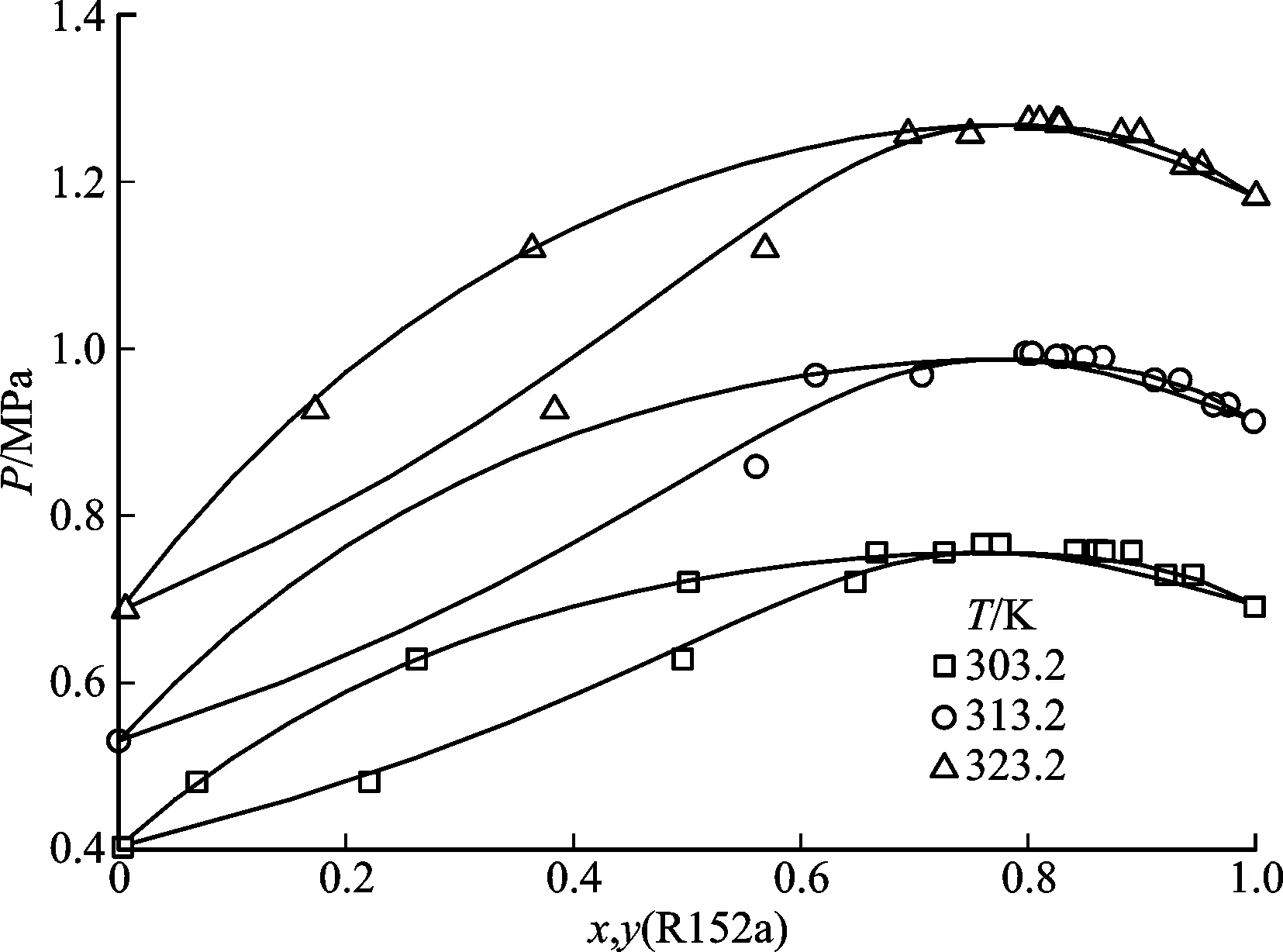
表4为详细的多元系统黏度性质计算值与文献实验值比对结果。但是对于部分含CO2系统,当系统温度升至300 K附近,模型计算值与文献值的偏差出现波动(见图3e),最大偏差可达29%(当含CO2五元混合系统的系统温度为313 K时)。此情况在系统中CO2组分占比变大时尤为明显。

(a)R125+R134a[35]

在近临界区,系统热力学性质对热力学状态的变化非常敏感,即处于近临界区的系统,其温度或压力即使发生微小的波动也可能会导致系统热力学性质产生较大的改变[28-30]。因此,热力学模型难以准确描述近临界区系统剩余熵是否是造成含CO2系统黏度计算结果与文献数据偏差较大的原因。此外,也可能是由于现有无量纲对比黏度混合法则不适用所导致。为避免由于近临界区热力学模型预测能力的恶化导致难以客观评价剩余熵黏度标度理论,本文借鉴文献[8,29]中提出的方法,在比对时剔除了近CO2临界区的实验数据。为此对于含CO2系统,表4中黏度偏差值Dη为仅包含系统温度低于295 K的数据点比对结果。根据表4中结果可以看出,在远CO2临界区(系统温度低于295 K),本文所得含CO2系统黏度计算结果与文献数据吻合良好,最大Dη小于4.66%。

表4 多元混合制冷工质系统黏度性质计算值与文献实验值比对结果

3 结 论

本文结合sPC-SAFT状态方程和基于链节的剩余熵黏度标度理论准确地描述和预测了不同工况下纯质与二元系统的液相黏度性质,并将其推广至三元及以上更复杂的混合制冷工质系统,其预测精度能够较好地满足工程实际需要。但同时比对结果表明该模型对于部分复杂系统的预测能力稍显不足,这可能是近临界区系统热力学性质随温度、压力变化波动较大导致的,而现有的高预测性混合法则不能很好地描述部分复杂系统近临界区的剩余熵,因此仍需基于统计缔合流体理论模型参数的物理内涵对现有混合法则展开更深层次的研究和改进。本工作能在一定程度上促进剩余熵黏度标度理论在多元复杂系统领域的推广,为其进一步的理论研究提供指导和借鉴。

(1)将制冷工质的无量纲对比黏度与sPC-SAFT状态方程给出的系统剩余熵相关联,获得一系列饱和状态下的多项式参数并成功应用于不同工况。此外,为了更好地与文献饱和液相黏度数据进行比对,系统研究了二元体系的汽液相平衡性质并给出相关二元作用参数。在此基础上,最终结合高预测性无量纲对比黏度混合法则,将该理论进一步推广至多元复杂混合系统。

(2)由剩余熵黏度标度理论计算得到的11种纯质黏度与文献实验数据间的最大绝对平均偏差小于4.36%,表明该模型能够非常准确地描述目标工质的纯质液相黏度性质。针对目标工质的汽液相平衡性质展开系统研究并给出相应二元作用参数,实验数据与本文计算值间的最大绝对平均偏差小于1.3%。基于此,本文系统比较了651个多元混合制冷工质系统的液相实验数据,在所比对的温度和压力范围内(233.40～369.15 K,0.17～9.93 MPa),模型计算偏差大于5%的数据点占7.9%,且偏差较大的数据点主要集中于近临界区的含CO2三元及五元复杂系统。