水下吸声超材料的质量集中效应

马承志,王立博,吴九汇

(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学机械结构强度与振动国家重点实验室,710049,西安)

共振型声学超材料具有对低频声的良好吸声性能,成为主流的吸声方法之一,近年来得到了广泛的研究。与传统材料相比,共振型声学超材料具有吸声系数高、结构尺寸小等显著优点。然而,诸如膜型超材料(MAMS)[1-7]、缠绕空间超材料[8-11]和亥姆霍兹谐振器[12-16]等几种共振型超材料存在一个主要的障碍,即由于局域共振机制,吸声范围可能仅限于一个狭窄的频带内。因此,如何拓宽吸声带宽是一个值得关注的重要问题。

近年来,共振型超材料的协同耦合特性引起了人们的广泛关注。具体来说,对于MAMS结构,主要有两种结构,分别对应于两种协同耦合行为。一种结构是在一个元胞上放几个振子。在此过程中,多个振子可以丰富元胞的共振模态,从而产生更多的吸声峰,使材料的带宽显著拓宽。另一个是多元胞阵列,每个元胞有一个振子产生一个单独的共振峰。通过这种方法,多元胞阵列的总振动幅值在声学虹吸[17]作用下大大提高,保证了结构在较宽的频率范围内仍能保持较高的吸声水平。受上述方法的启发,近年来在空气中宽带低频吸声的尝试越来越成功[18],同时水下吸声也有不错的研究进展[19-30]。但是,如何在水下以低厚度超材料实现低频段吸声仍是我们急需解决的问题。

由于水和空气的特性阻抗差异巨大,这种膜型超材料应该被薄板型超材料取代,这种薄板型超材料是由一块薄钢板和铅块振子组成,薄钢板取代了膜型超材料中的硅胶薄膜,同时,因为钢的刚度是硅胶薄膜的几倍,这意味着为了使结构在相同频率处的达到共振,薄板型超材料需要比膜型超材料中使用更重的振子才能达到低频吸声性能。因此,当截面形状保持不变时,振子的厚度会显著增加,这无疑不利于实际应用。

为了实现低厚度的超材料,本文提出了质量集中效应的一般设计概念。传统的薄板型超材料是通过一个厚振子的振动产生吸声峰,而利用质量集中效应的薄板型超材料可以通过相邻两个薄振子集中获得相同的吸声性能,同时出现额外的吸声峰,具有多个模态。这意味着在保持原有吸声性能基本不变的情况下,不仅可以大幅度降低超材料的厚度,还能提高超材料的吸声性能。同时,分析了分离振子的距离和质量差对吸声系数的影响,并利用声阻抗匹配机理解释了吸声的物理机理。在此基础上,提出了一种多元胞结构,该结构在200～1 000 Hz范围内具有良好的宽带吸声效果。

1 基于质量集中效应的模型

1.1 仿真模型

为了说明质量集中效应,图1给出了两种结构,具有质量集中效应的双振子结构M1和传统的单振子结构M2。具体而言,M1结构由3部分组成:一块矩形薄钢板、两个相对的半圆型铅块振子,如图1a所示。同样,M2结构也是由3部分组成,唯一不同的是只有一个振子固定在钢板上,如图1b所示。M1和M2中薄板的宽度、长度和厚度分别为S1=50 mm,S2=60 mm,h=0.3 mm。此外,M1和M2中振子的半径均为r=19 mm,M1中振子的厚度均为t1=30 mm,而M2中振子的厚度为t2=60 mm,M1中分离振子之间的距离为l=1 mm。仿真中使用的材料参数如表1所示。

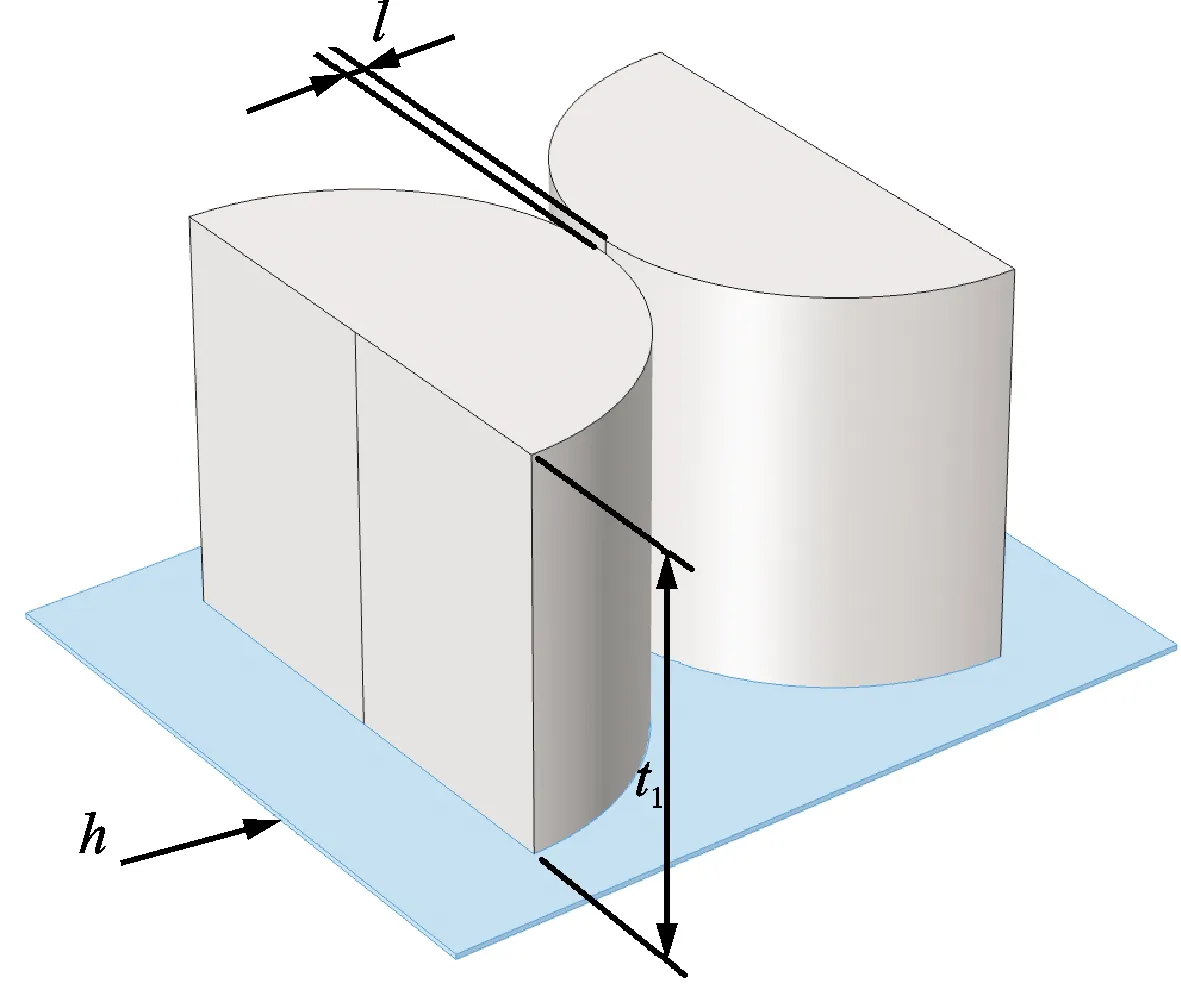
(a)基于质量集中效应的双振子结构M1

表1 仿真中使用的材料参数

为了获得该超材料的吸声性能,利用商用有限元软件COMSOL MultiphysicsTM 5.5建立了声-固耦合的有限元仿真模型。薄板、振子被定义为固体域,其余部分被定义为声学域;沿元胞结构法线方向,将平面入射波(P=1 Pa)垂直地施加于该超材料表面;边界条件设置为固定约束,该约束施加在薄板的外边缘;材料参数和几何尺寸与上述参数保持一致。此外,水的密度和水中的声速分别ρ0=1 000 kg/m3和c0=1 500 m/s。

1.2 声场计算模型

图2所示为声场简化示意图,根据能量守恒定理,入射声波Ii由以下3部分组成:反射声波Ir、透射声波It以及声能转化为结构共振后所耗散的能量Iα。因此,该超材料所耗散的能量Iα可以表示为

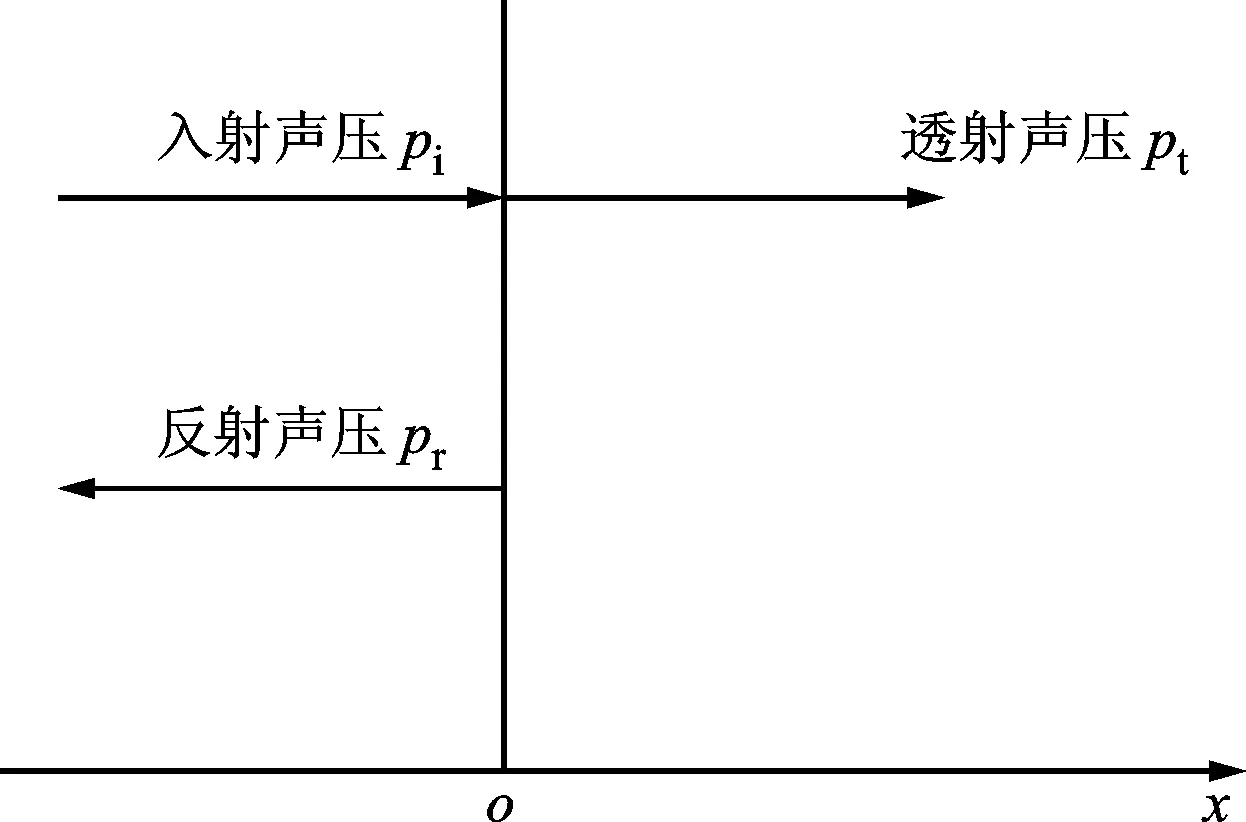
图2 声场简化示意图

Iα=Ii-Ir-It

(1)

声强吸声系数α定义为Iα和Ii的比值

(2)

式中:RI为声强反射系数;TI为声强透射系数[31]。

在不考虑声波传播过程中媒质损耗问题情况下,薄板振子吸声结构的吸声系数α≤50%[32],即

(3)

此时,由吸声峰值处声阻抗匹配原理可知,声阻抗率表达式为

Zs=Rs+jXs

(4)

式中:Rs为声阻率;Xs为声抗率。

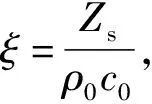
ξ=xs+jys

(5)

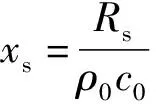
当ξ=1时,xs=1,ys=0,吸声系数α达到最大值0.5,这就说明超材料的吸声系数与它的声阻抗之间有着十分密切的关系。当Zs=ρ0c0时,超材料的结构阻抗与介质的特性阻抗是匹配的,具有良好的吸声性能。

2 质量集中效应的低频多模态宽带吸声物理机理

图3a、3c、3d、3e分别给出了M1和M2的吸声系数以及各情况下吸声峰对应的振动模态。由图3a可以明显看出,两种结构在180 Hz处都产生了一个吸声峰,最大吸声系数几乎相同,为0.48。此外,M1在335 Hz处出现了另一个吸声峰,吸声系数为0.405。图3c、3d、3e分别给出了结构的振动模态和振幅,可以清楚地看到,在每种情况下,吸声峰都与振子的共振有关。具体来说,在M1情况下,第1个吸声峰对应于振子内部的强平移运动,第2个吸声峰可归因于振子外部的旋转运动。同样,对于M2情况,唯一的吸声峰是由振子的强平移运动产生的。

图3b为M1和M2的总弹性应变能。可见,在振子振动的作用下,总弹性应变能在180 Hz和335 Hz处显著增强,将入射声能转化为弹性应变能后通过结构阻尼进行耗散,从而提高吸声系数。

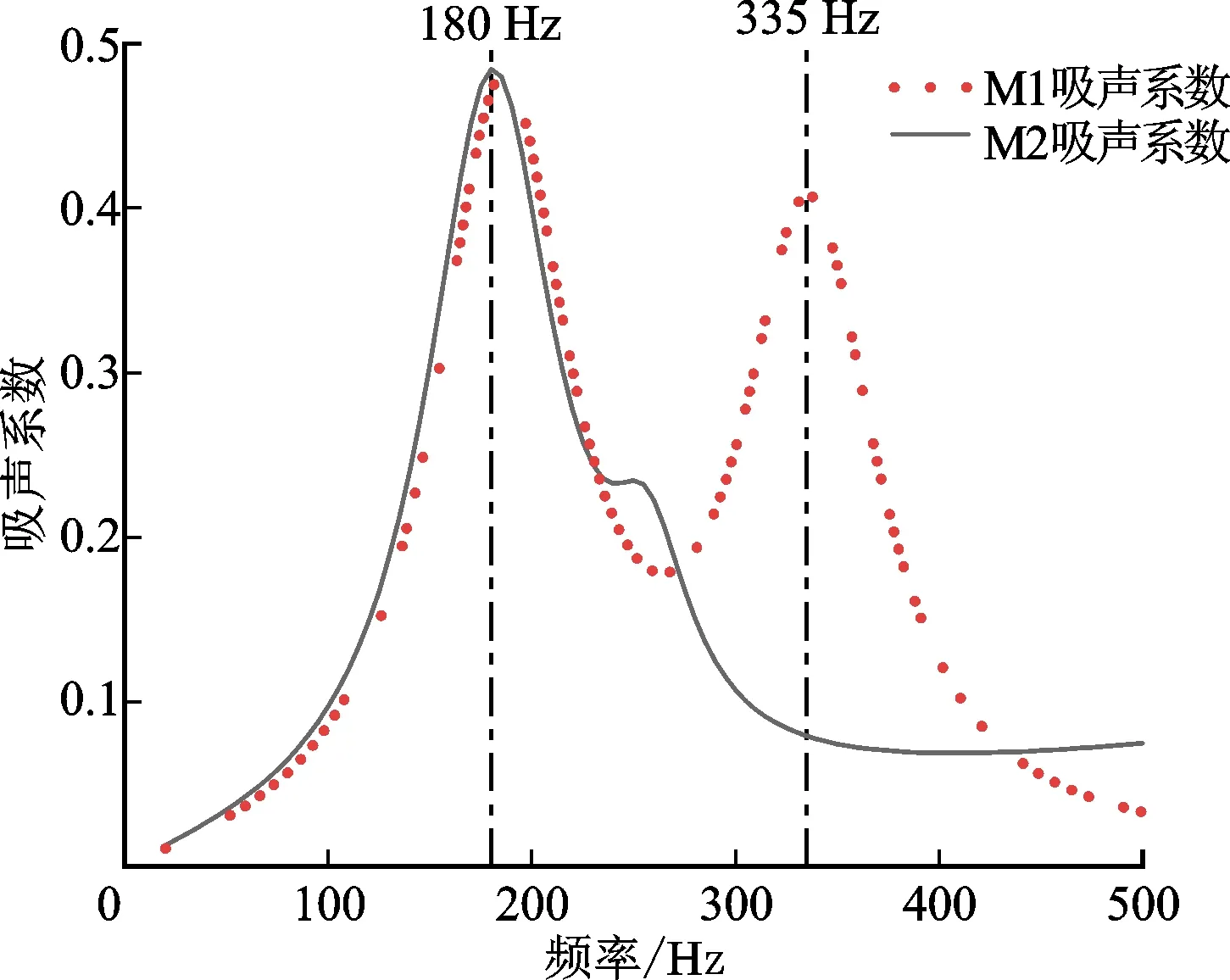
(a)M1和M2的吸声系数

值得强调的是,上述研究中M2振子厚度等于M1振子的总厚度,这意味着M1和M2振子的总重量相等。在这种情况下,与M2结构相比,通过适当设计M1的结构可以获得类似的第1个吸声峰和1个附加吸声峰,同时振子厚度大幅度降低,结构变薄,这种现象可以描述为质量集中效应。

为了更好地研究质量集中效应背后的物理机理,我们对M1和M2的阻抗特性进行了研究。M1和M2的阻抗特性如图4所示。在M1中,需要注意180 Hz和335 Hz两处,180 Hz时声阻率比xs为1.52,非常接近于1,声抗率比ys等于0。根据声阻抗匹配机理,该处存在一个吸声系数相当高的吸声峰。同时,在335 Hz处的声阻率比xs和声抗率比ys都接近理想吸声的假设情况,因此在335 Hz时出现另一个吸声峰。与180 Hz相比,335 Hz时的声阻率比和声抗率比分别离1和0有一定距离。因此,335 Hz时的最大吸声系数应小于180 Hz时的最大吸声系数,这与图4的结果一致。

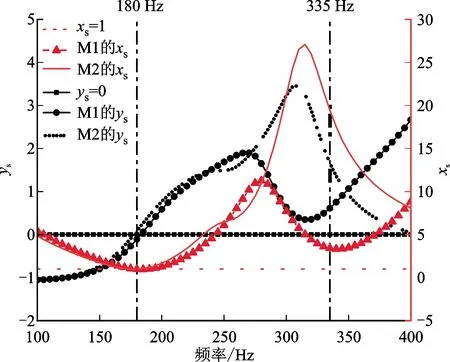
图4 M1和M2的声阻抗率比情况

在M2结构中有两点需要注意,同样是180 Hz和335 Hz两处。180 Hz时的声阻率比为1.53,声抗率比为0,可以保证吸声峰具有近乎完美的吸声系数。335 Hz时的声阻率比和声抗率比远离1和0,意味着在335 Hz时不会出现明显的吸声峰,这也可以在图4中得到证实。

3 关键参数对吸声性能的影响

3.1 分离振子间距离对吸声情况的影响

首先,为了探究M1结构下振子之间的距离D对吸声系数的影响,研究了以下几种情况:情况1.1,D=0 mm;情况1.2,D=2 mm;情况1.3,D=4 mm;情况1.4,D=6 mm;情况1.5,D=8 mm。

为了更直观地展示振子间距对吸声性能的影响,对情况1.1～1.5的吸声系数和吸声峰的频率进行了总结,如表2和表3所示。

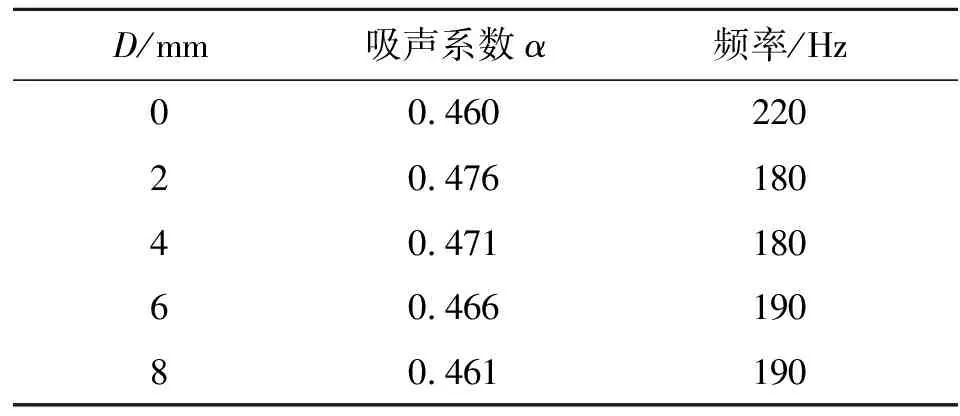
表2 第1个吸声峰的吸声系数和频率

表3 第2个吸声峰的吸声系数和频率

振子间不同距离的M1结构吸声情况的数值模拟结果如图5所示。对于第1个吸声峰,可以清楚地看出,在D不为0的情况下,虽然两个振子之间的距离越远,但是吸声系数变化不大。随着D从2 mm增大到8 mm,吸声系数从0.476减小到0.461,当D=0时,吸声系数为0.46。具体来说,情况1.1～情况1.5中第1个吸声峰的频率分别为220、180、180、190和190 Hz,可以看出,当D从2 mm增加到8 mm时,吸声峰的频率变化不大;当D=0 mm时,此时两振子合并为一个整体,吸声峰的频率向高频移动,具有良好的吸声性能。

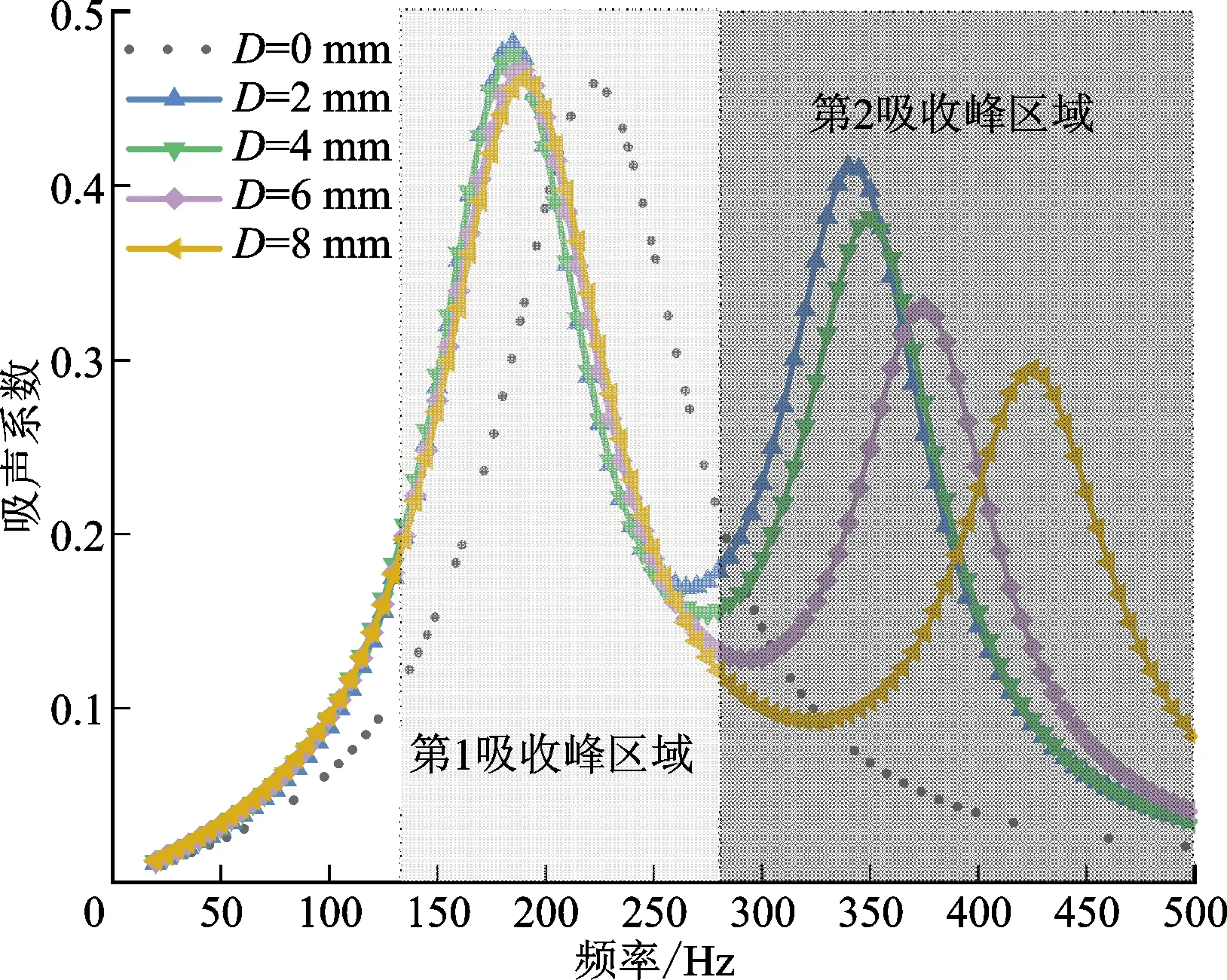
图5 振子间不同距离的M1结构吸声情况

对于第2个吸声峰,随着D的增加,吸声峰的最大吸声系数和吸声峰的频率都有明显的变化,即随着D从2 mm增加到8 mm,吸声峰从0.41下降到0.29,同时,吸声峰的频率向更高的频率范围移动;当D=0 mm时,由于两振子不相互独立,无法通过振子外部的旋转运动所产生的共振来进行吸声,因此在0～500 Hz范围内没有第2个吸声峰。

为了充分理解阻抗特性与吸声系数之间的关系,图6给出了情况1.1～1.5中吸声峰处的阻抗特性。从图6a中可以明显看出,随着D的增大,阻抗特性略微变化,导致吸声系数略有变化。以D=2 mm和D=4 mm为例,来充分理解这种现象。在D=2 mm的情况下,声阻率比和声抗率比分别为0.683和0.19,当D=4 mm时,声阻率比和声抗率比分别是0.644和0.18。因此,由声阻抗匹配原理,可以得到不同的吸声系数,分别为0.476和0.471。同样,对于第2个吸声峰区域,如图6b所示,随着D的增大,因为声阻率比和声抗率比分别远离1和0,吸声系数显著降低。

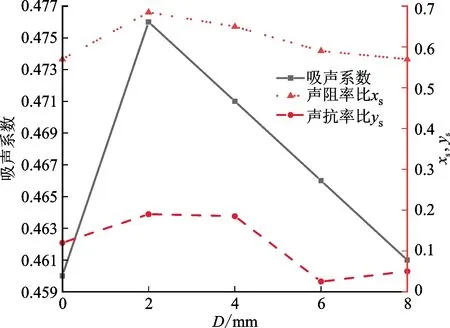
(a)第1吸声峰区域

3.2 分离振子间质量差对吸声情况的影响

紧接着,对结构的另一个关键参数振子的质量差进行了深入研究,图7所示为不同振子的质量差与吸声系数的关系。值得注意的是,由于所有振子都采用相同的材料和截面面积,不同振子的质量差可以用振子的厚度差T来表示,在这里振子的总质量保持不变。

图7 振子间不同厚度差的M1结构的吸声情况

情况2.1: 30 mm/30 mm,总厚度为60 mm,厚度差T=0 mm。

情况2.2: 35 mm/25 mm,总厚度为60 mm,厚度差T=10 mm。

情况2.3: 40 mm/20 mm,总厚度为60 mm,厚度差T=20 mm。

情况2.4: 45 mm/15 mm,总厚度为60 mm,厚度差T=30 mm。

为了更清楚地描述结果,我们总结了情况2.1～2.4的吸声系数和吸声峰的频率,如表4和表5所示。可以清楚地看出,对于第1吸声峰区域,随着振子厚度的增加,吸声峰频率不变,吸声系数略有提高。在第2个吸声峰区域,随着振子厚度的变化,吸声系数和吸声峰频率的变化显著,吸声系数逐渐提高,频率向高频移动。

表4 第1个吸声峰的吸声系数和频率

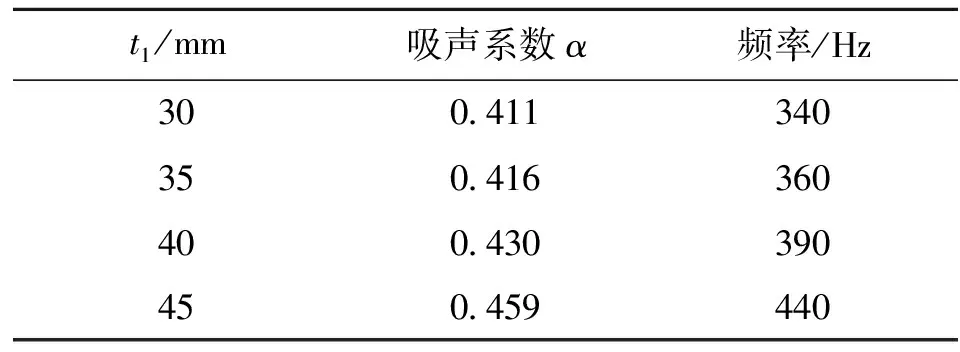
表5 第2个吸声峰的吸声系数和频率

结构的阻抗特性与吸声系数的关系,如图8所示。在图8a中,由于声阻率比和声抗率比变化都很小,所以在第1个吸声峰区域的吸声系数几乎没有变化。这里以T=10 mm和T=20 mm为例,声阻率比由0.681 4变为0.684 2,声抗率比由-0.172 2变为-0.132。因此,最大吸声系数从0.477增加到0.480。另一方面,对于第2个吸声峰区域,同样超材料越满足阻抗匹配条件,吸声效果越好,如图8b所示。

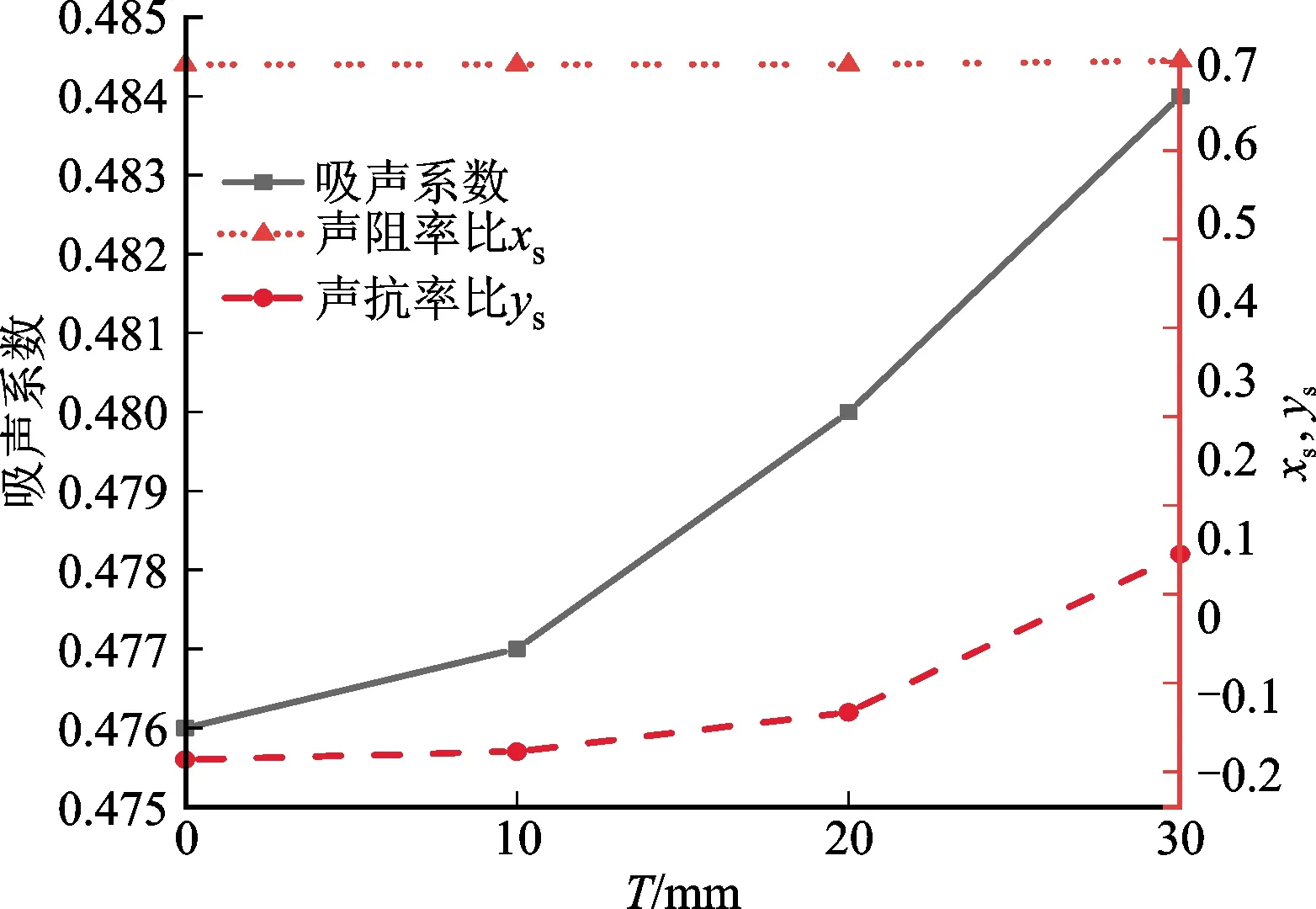
(a)第1吸声峰区域

4 质量集中效应作用下的多模态低频宽带吸声超材料

基于上述分析,图9a给出了一种基于质量集中效应的多模态低频宽带吸声超材料,该超材料由9个基本元胞并联布置构成。具体来说,超材料的整体尺寸W=150 mm,L=180 mm,H=30 mm。

通过对每个元胞结构进行设计,使得每个元胞在所设计的频率段内能够产生高效吸声效果。通过多元胞的并联布置,在声学虹吸效应的作用下,各个元胞分别在对应共振频率段发生强烈振动如图9b所示。通过振型图可以看出,600 Hz以下的吸声,主要是通过每个元胞中振子内部强平移运动所产生的第1吸声峰进行吸声,在600 Hz处及以上频率,主要是通过每个元胞中振子外部的旋转运动所产生的第2吸声峰进行吸声,从而使得该超材料在各个频率段都具有高效吸声效果以及低的厚度。基于质量集中效应实现了200～1 000 Hz的多模态低频宽带吸声效果,如图9c所示。

(a)超材料模型

5 结束语

在本研究中,在保持总质量不变的情况下通过将单一振子的高度精确地划分为相邻的两个薄振子,可以获得类似原单一振子的吸声峰和一个附加吸声峰,增加了一个共振吸声模态,吸声性能大大提高,同时振子高度大幅度降低,超材料厚度急剧下降,结构变薄,这种现象我们描述为质量集中效应。我们利用声阻抗匹配机理解释了该超材料吸声的物理机理,探究了分离振子的距离和质量差对吸声系数的影响,得出来非常重要的规律。最后,提出了一种低厚度超材料,该超材料在200～1 000 Hz范围内具有良好的宽带吸声效果。总之,基于质量集中效应,将为水下低厚度的多模态低频宽带吸声超材料设计提供有效的指导,显示出巨大的水下声波控制潜力,具有实际工程应用意义。