基于Tensor Train分解的Sylvester张量方程求解
2021-12-03吴玉倩陈中明
吴玉倩,陈 荣,陈中明
(杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
Sylvester张量方程是一类重要的张量优化问题,广泛应用于控制系统、图像处理、模型降阶和流体力学等领域。文献[1]在求解热辐射领域的三维辐射传递方程时,采用Chebyshev配置点谱方法进行离散化,并提出了三阶Sylvester张量方程,给出一种基于Schur分解的直接解法。文献[2]给出了一种预处理迭代法。目前已有的一些用于求解Sylvester张量方程的方法,如Schur分解法、Krylov子空间法[3]等,往往需要直接存储整个张量数据,其元素个数随着阶数呈指数增长,在求解高阶Sylvester方程时,这些算法面临巨大的存储量和计算量等问题[4]。为此,本文提出一种基于Tensor Train分解的交替随机梯度下降法,有效降低了计算复杂度。
1 问题模型
本文中,Sylvester张量方程如下:

(1)

(i1…ik…id
当d=2时,方程(1)退化为Sylvester矩阵方程
AX+XBT=C
2 TT分解
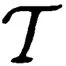

vec()=G1,G2,…,Gd
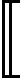
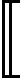
下面介绍本文用到的相关定义和性质,更多有关张量TT分解的运算,包括张量加法、范数等参见文献[5]。
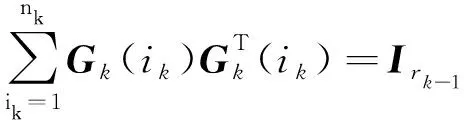


Pk+1=(Ink⊗Pk)reshape(Gk,rk-1nk,rk)(Ink⊗Pk)Lk
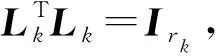
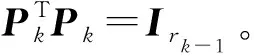
3 交替随机梯度下降法
本文提出的交替随机梯度下降法(简称TT-SGD),采用随机采样的思想。首先,运用张量TT格式下的模乘运算,将方程(1)左边转化为TT格式;然后,运用交替最小二乘法(Alternating Least Squares Method,ALS)依次更新TT核,并得到子问题;最后,对子问题中的系数矩阵进行随机采样。关于TT格式下ALS方法的收敛性分析可参考文献[7]。
将式(1)向量化后,转化为求解最小二乘问题,得到:
(2)
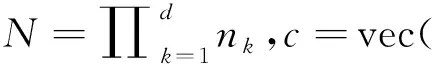
A=Ind⊗…⊗In2⊗A(1)+…+A(d)⊗Ind-1⊗…⊗In1
其中,gk=vec(Gk)∈Rrk-1nkrk。在ALS中,分别固定d-1个核G1,…,Gk-1,Gk+1,…,Gd,依次更新核Gk,相应子问题的目标函数可写成:
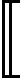
(3)

由定义可知,当阶数d很大时,无法直接计算梯度fk(gk),于是考虑对Hk的行进行随机采样。首先,给出矩阵Hk另一种等价形式。对于式(1),令



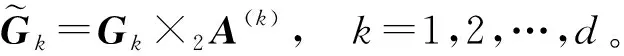

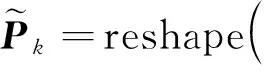
于是有:

由此,得到关于gk=vec(Gk)系数矩阵的另一种等价表示
(4)

(5)
(6)
(7)
TT-SGD具体流程如下。

输入:矩阵{A(k)}dk=1,张量,采样数NS,TT秩{rk}dk=0,相对误差ω=1,算法精度0<ε<1输出:构成张量的TT核{Gk}dk=1初始化右正交化核{Gk}dk=2while ω>ε 随机采样得到指标向量集S,按式(6)从右往左计算采样矩阵Qk,1和Qk,2 for k=1,2,…,d 根据式(4)计算采样系数矩阵Hk,再根据式(7)计算随机梯度∇fk(gk) 更新gk←gk-α∇fk(gk),并左正交化核Gk 根据式(5)计算采样矩阵Pk,1和Pk,2 end 计算相对误差ω=Hkx-c22/c22end输出核Gk(k=1,2,…,d)
4 收敛性分析
在第t步迭代更新TT核Gk中,相应子问题(3)的目标函数记为:
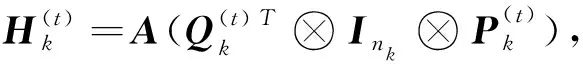
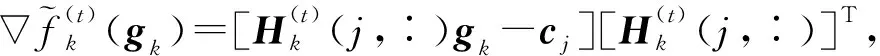
对式(2)中的函数f(x)做出如下假设:

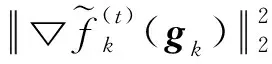
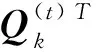
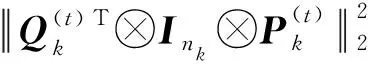
于是有
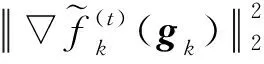
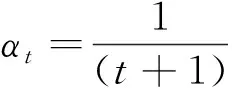
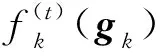

(8)
式中,δ是系数矩阵A的最大奇异值。
(9)
(10)

设f*是f(x)的最优值,故E[f(x(T))]≥f*,于是有:
令αt=1/(t+1),当迭代步数T趋向无穷大时,有:
证毕。
5 数值实验

(11)


图1 相对误差随迭代次数变化情况
从图1可以看出,由于采用随机梯度,相对误差并非单调下降,但随着迭代次数增加,相对误差逐渐趋于稳定,并达到给定精度,TT-SGD算法收敛。


表1 不同精度下不同算法的运行时间 单位:s
从表1可以看出,与PM-BTF算法相比,TT-SGD算法达到相同精度所需的运行时间更短;且随着算法精度的提高,2种算法运行时间的差距更大,TT-SGD算法的优势更明显。因为PM-BTF算法直接处理张量数据,而TT-SGD算法采用随机梯度交替更新TT核,有效降低了算法的复杂度。
6 结束语
针对Sylvester张量方程,本文提出一种基于TT分解的交替随机梯度下降法。运用TT格式紧凑的形式,有效降低了算法的存储和计算复杂度,通过对子问题中系数矩阵的随机采样,实现了大规模问题的求解。下一步将针对更有效的随机采样方法展开研究。
