多旋翼无人机旋翼风场分布情况研究∗
2021-12-03周川川李傲梅
周川川 李傲梅
(陆军炮兵防空兵学院信息工程系 合肥 230031)
1 引言
近年来,许多高校及企业都有开展风测量新方法的研究[1],其中尝试运用旋翼无人机搭载风探测设备对空中风进行测量的研究较多,而对于风探测设备的选择又多以超声波测风设备作为优选方案。由于传统的超声波测风设备实现对风场的精确测量需要以稳固的搭载平台为前提,因而为实现旋翼无人机与超声波测风设备的有效配合,研究重点主要集中在了以下几个方向。
1)通过研究旋翼无人机的拓扑结构,对无人机机架结构进行优化,以增强无人机平台空中静止时的抗扰动性[2];
2)通过分析旋翼无人机的飞行特点,针对风力等作用导致的机体摇摆问题设计出相应的自抗扰算法,通过计算平衡性偏差,然后对偏差进行修正,达到实时调整无人机的飞行姿态、保持平台平稳性的目的[3];
3)收集无人机平台摇摆数据,结合超声波测风原理,通过分析研究二者之间关联关系进而设计出相应的抵消算法的方式修正初始数据,得到测算数据[4];
4)由于超声波测风的优点是能够感应到微小气流的变动,所以旋翼引发的气流会对其测量数据形成干扰。通过研究旋翼风场分布规律[5],将测量器件安装在干扰风场之外的区域,以减小甚至避免旋翼风场对测量数据的影响,是保证数据准确性的一种设计思路。本文的研究目的即在于此。
本文选择从流场分析着手,基于计算流体动力学(CFD)方法,利用Fluent软件对四旋翼及六旋翼无人机旋翼产生的风场进行仿真,以期通过分析旋翼风场范围特点,为优化旋翼无人机测风系统的布局设计提供思路,达到用布局优化方式提高探测精度的目的。
2 Fluent仿真原理
2.1 CFD方法概述
本文选取的数值计算分析软件为ANSYS Flu⁃ent,其使用的是有限体积法,将整个计算区域划分为网格,并使每个网格点周围有一个互不重复的控制体积,将微分方程对控制体积积分,得到离散方程[6]。基于ANSYS Fluent软件运用CFD方法进行的求解过程如图1所示。
2.2 有限体积法(FVM)
有限体积法(Finite Volume Method)又称为控制体积法(Control Volume Method),其基本思路是将计算区域划分为网格,并使每一个网格点周围有一个互不重复的控制体积;将待解微分方程(控制方程)对每一个控制体积积分,从而得出一组离散方程。其中的未知数是网格点上的因变量。为了求出控制体体积的积分,必须假定因变量的值在网格点之间的变化规律。从积分区域的选取方法看来,有限体积法属于加权余量法中的子域法,从未知解的近似方法来看,有限体积法属于采用局部近似的离散方法。简言之,子域法加离散,就是有限体积法的基本方法。而控制方程被离散化以后,就可以对其进行求解,常用的算法包括SIMPLE算法、SIMPLEC算法和PISO算法[7]。
2.3 流体区域离散
首先确定计算区域,计算区域设定完成后,对计算区域进行离散化处理,根据需求将其划分成苦干子区域,从而生成网格。通过设定节点位置方式,以节点代替网格以参与到具体的控制方程计算当中,以此达到网格中的控制方程离散化目的。通过此步骤,偏微分格式的控制方程转化为各个节点上的代数方程组。
2.3.1 计算区域的离散
当前应用中,离散网格划分一般分为结构化网格和非结构化网络两种类型。结构化网格生成速度快、结构简单,缺点是不能实现对复杂边界区域的划分,而非结构化网格对复杂边界划分效果较好,但网格划分过程复杂,生成速度慢。用户可以根据需要选择不同类型进行网格划分。
2.3.2 控制方程的离散
控制方程的通用形式为
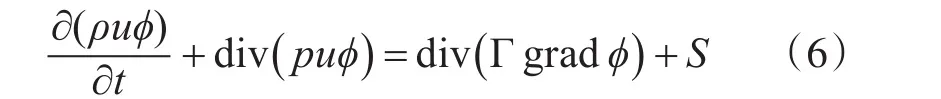
式中,ϕ为广义变量,可以为速度、温度或浓度等一些待求的物理量;Γ为相应于ϕ的广义扩散系数;S为广义源项。
2.3.3 常用的离散格式
节点作用是用其数值代替控制体作为离散方程的输入值,求出值近似替代控制体界面物理量。Fluent软件中有限体积法的对流项离散格式主要体现在Cell界面值的选取上,常见的有一阶迎风格式,二阶迎风格式,一阶迎风格式取迎风侧Cell上的物理量值,二阶迎风在这个取值基础上加上Cell上梯度乘以面与Cell中心的距离矢量,其他高阶格式有QUICK格式,MUSCL格式。
2.4 CFD基本方程
在CFD数值模拟计算时,可将这些物理守恒定律归纳几个方程来表示,即质量守恒方程、动量守恒方程、能量守恒方程,此三个基本方程为CFD的理论基石[8~9],当流体研究中不考虑热交换问题时,能量守恒问题可不考虑,可以只考虑前两个方程。
1)质量守恒方程:
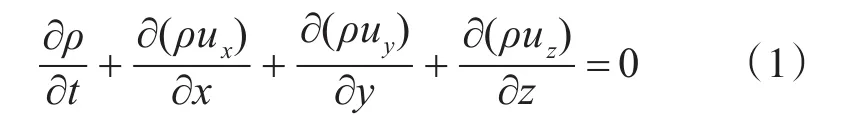
式中,ux、uy、uz分别为x、y、z三个方向的速度分量(m/s),t为时间(s),ρ为密度(kg/m3)。
2)动量守恒方程:
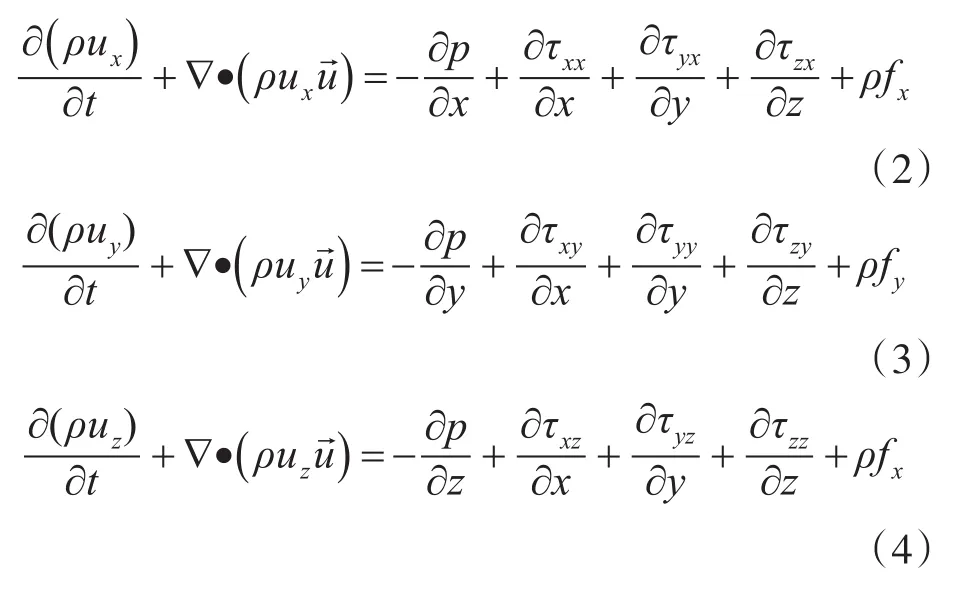
式中,p为流体微元体上的压强(Pa),τxx、τxy、τxz等代表微元体表面上粘性应力分量(Pa),fx、fy、fz为三个方向的单位质量力分量(m/s2),当质量力只受重力,且z轴垂直向上时,fx=fy=0,fz=-g。
3)能量守恒方程:
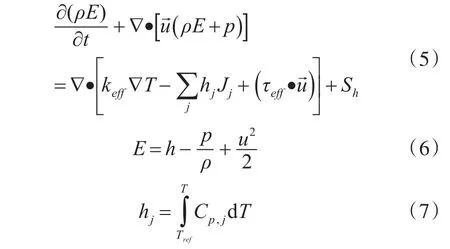
式中,E为流体微团包含内能、动能和热能的总能(J/kg),h为焓(J/kg),hj为组分j的焓(J/kg),Tref=298.15K;keff为有效热传导系数(W/(m·K)),keff=k+kt,kt为湍流热传导系数;Jj为扩散通量;Sh为包括化学反应热及其他用户定义的体积热源项。
2.5 湍流模型
Fluent的湍流模型一直处于CFD软件的前沿,其提供湍流模型较为丰富,主要包括无粘模型(In⁃viscid)、层流模型(Laminar)、SA模型、k-ε模型、k-ω模型、3方程转捩模型、4方程转捩模型、雷诺应力模型、SAS湍流模型、分离涡模型、大涡模拟模型。
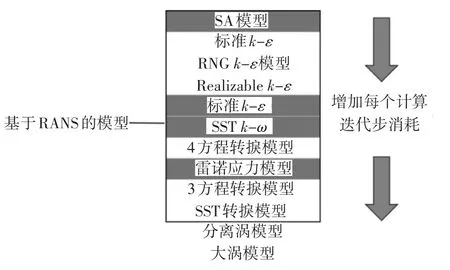
图2 湍流模型的计算开销
CFD软件的目的在于将计算流体动力学方法应用于工程设计中,一般的CFD软件应用过程通常包含三个步骤:计算前处理、计算求解、计算后处理。这三个部分可以集成于同一软件内,也可以分属不同的软件。对于CFD工程应用的一般流程如表1所示。

表1 CFD工程应用一般流程
3 旋翼无人机建模及其流场仿真
3.1 仿真模型的建立
为了确定螺旋桨旋转产生风场的详细分布情况,本研究中仅把旋翼数目作为变量,旋翼转速、旋翼尺寸、机架结构、螺旋桨桨叶数量及桨叶形状均作为固定量,以减少对本研究内容的干扰。其中,机架结构采用“×”型机身,旋翼数量选用四旋翼和六旋翼两种类型,转速采用5000转/分钟,桨叶数量选用两叶,桨叶形状以4730F桨叶为参照,四旋翼及六旋翼无人机间距比均设定为1,在3DMAX软件上搭建机身、机架及旋翼模型并调整模型参数生成stp文件,用Hypermesh和ICEM CFD分别对模型进行面网格及体网格的构建,利用Fluent软件作为求解器对网格模型进行计算,最后利用CFD-Post软件对Fluent软件生成结果进行后处理。
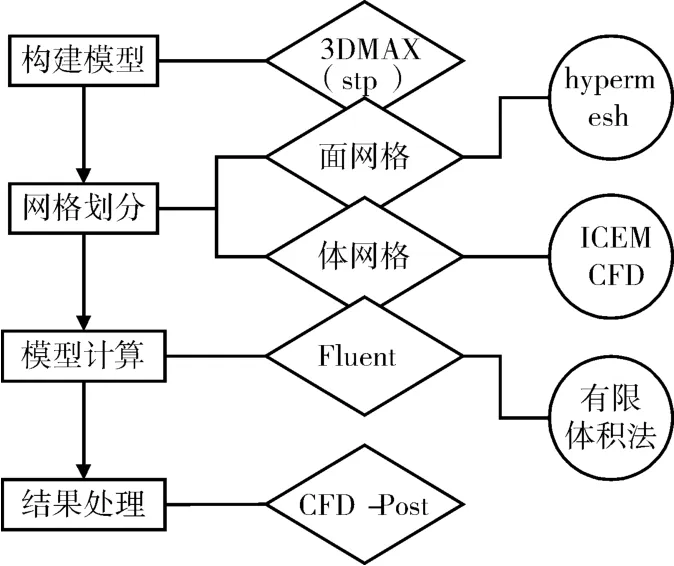
图3 建模及仿真流程框架
3.2 网格划分
本研究中对于设定的流体区域,整个区域初始状态默认为静止状态,即假定无空气流动。考虑到旋翼旋转后,旋翼周边空气流动迅速,而距旋翼较远区域空气流动缓慢,故将整个流体计算域分成多个部分:旋翼旋转设定为旋转域,其余部分设定为静止域。又由于对因旋转速度引起的风场分布测算为瞬态计算,所以旋转域采用非结构化网格,设定更加细密网格划分,而静止域网格划分由于距旋翼相对较远,受旋翼影响小,故网格设定相对稀疏。
3.3 边界条件设定
将旋翼所在的旋转区域设定为绕旋翼中心旋转的滑移网格,由于要平衡旋翼旋转产生的力矩,相邻两旋翼转向相反,转速设定为5000rpm。旋翼边界设定为与连接域同步转动的moving wall。旋转区域和静止区域边界设置为interior。
3.4 结果分析
3.4.1 四旋翼无人机
四旋翼无人机在间距比为1情况下,叶片转速与无人机机体压力瞬时情况如图4、图5所示。图4、图5中颜色分别表示速度大小和压力强弱。由图中可看出叶片外沿转速最快位置,速度达到约100m/s,而从图5相同位置处可看出其位置所受气体压力最小。

图4 四旋翼无人机速度瞬时云图

图5 四旋翼无人机压力瞬时云图
从图6中可以看出,旋翼高速旋转过程中,在叶片后下方有形成一个三角形区域,相比较其他区域,此区域气流流动最快速,风速约为20m/s;其次是旋翼外沿旋转途经的环形区域。与此同时,其产生的气体压力情况从图7可以看出,总体上气体流动快的区域气压值相应最低,但也会略有不同:叶片后下方三角形区域内气体流动速度最快,但此区域对应的气压值并非最低,气压值最低区域集中在了叶片外沿轨迹形成的圆环当中。以此可推断,气流从叶片中央上方流入,而在叶片旋翼产生的离心力作用下气流有向叶片外沿流动的趋势,进一步断定气流在从上往下经过叶片后,并非只受叶片正直向下的作用力,离心力同样作用于气流,可进一步推断无人机中央位置正下方存在一个漏斗区域,此区域内气流流速较慢,气体扰动较小。

图6 四旋翼无人机叶片横截面速度瞬时云图
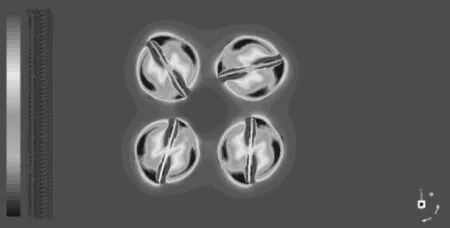
图7 四旋翼无人机横截面压力瞬时云图
为了更加直观地观察分析,如图8所示,在竖直切面上,可以印证以上猜想,旋翼通过旋转,将上方的气体螺旋向下吸入旋转,然后向下喷出,但无人机正下方存在一漏斗形区域,此位置气体流动缓慢,但其被快速流动气流所包围,因此不能作为测风传感器的理想安装位置进行考虑。

图8 四旋翼无人机竖直截面速度瞬时云图
运用到现实环境,可以推导出根据“X”形四旋翼无人机的尺寸不同、间距比不同,其流场范围也会有所差异,但流场特征不会改变。即静风区域的范围会有区别,但形状不会有大的区别。
基于以上分析,对气体流动进行测量的测风传感器而言,四旋翼无人机的正上方某一高度以上及无人机旋翼旋转形成的范围以外为测风传感器的理论安装区域,在此区域安装的传感器受旋翼旋转形成的气流扰动影响较小,可以最大限制保持传感器的测量精度和准确性。
3.4.2 六旋翼无人机
六旋翼无人机与四旋翼无人机飞行原理相似,从图9、图10中可以看出,六旋翼无人机压力特征遵循的规律跟四旋翼无人机也十分相似,但随着旋翼数的增加,无人机旋翼到无人机中心的距离增大,机身上下的相对静风区的范围也随之增大,如图11所示。

图9 六旋翼无人机压力瞬时云图

图10 六旋翼无人机横截面压力瞬时云图
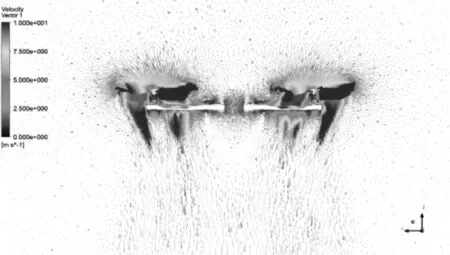
图11 六旋翼无人机横截面速度瞬时矢量图
此外,六旋翼无人机虽动力源增多,但旋翼转速仍设定为5000rp,在不考虑旋翼形状、叶片数目、叶片尺寸情况下,气体流动速度与旋翼转速成正比关系,即旋翼转运引起的气体流动速度没有变化,最大值仍旧约为20m/s,如图12所示。同时,根据图13可以看出,旋翼转动时,流过旋翼的气体除来自旋翼正上方以外,更多的是来自无人机外围区域,气体向旋翼上方汇聚,而后流过旋翼,经过叶片作用加速向斜下方喷出。
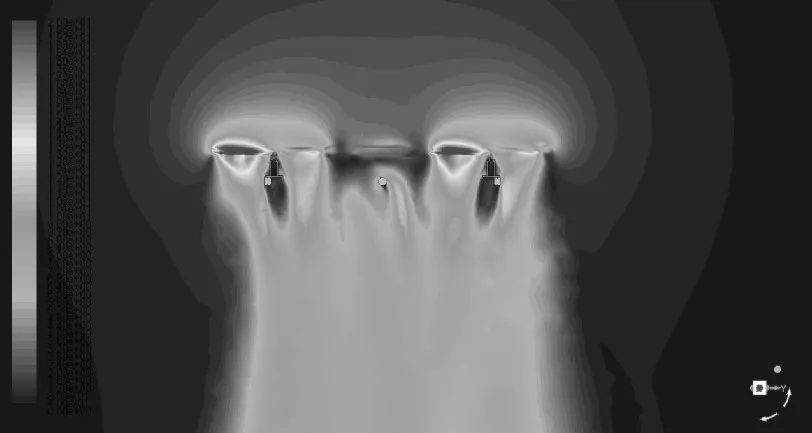
图12 六旋翼无人机竖直截面速度瞬时云图

图13 六旋翼无人机竖直截面速度瞬时流线图
由于旋翼数目增加,六旋翼无人机飞行稳定性更加突出,且旋翼动力相同情况下,负载能力增强;当重量相同,六旋翼无人机平均分配到每一个旋翼的升力配额变小,转速要求变低,旋翼转动对流场的影响也相应降低。但六旋翼无人机间距比大,即使相同间距比情况下,机身尺寸相比四旋翼无人机更大,受气流流动方向影响也更加明显。
4 风场影响及优化建议
4.1 旋翼风场对超声波测风方法的影响
一个完整的多旋翼气象无人机的结构[10]如图14所示。本节主要探讨旋翼风场对超声波测风仪器的影响。
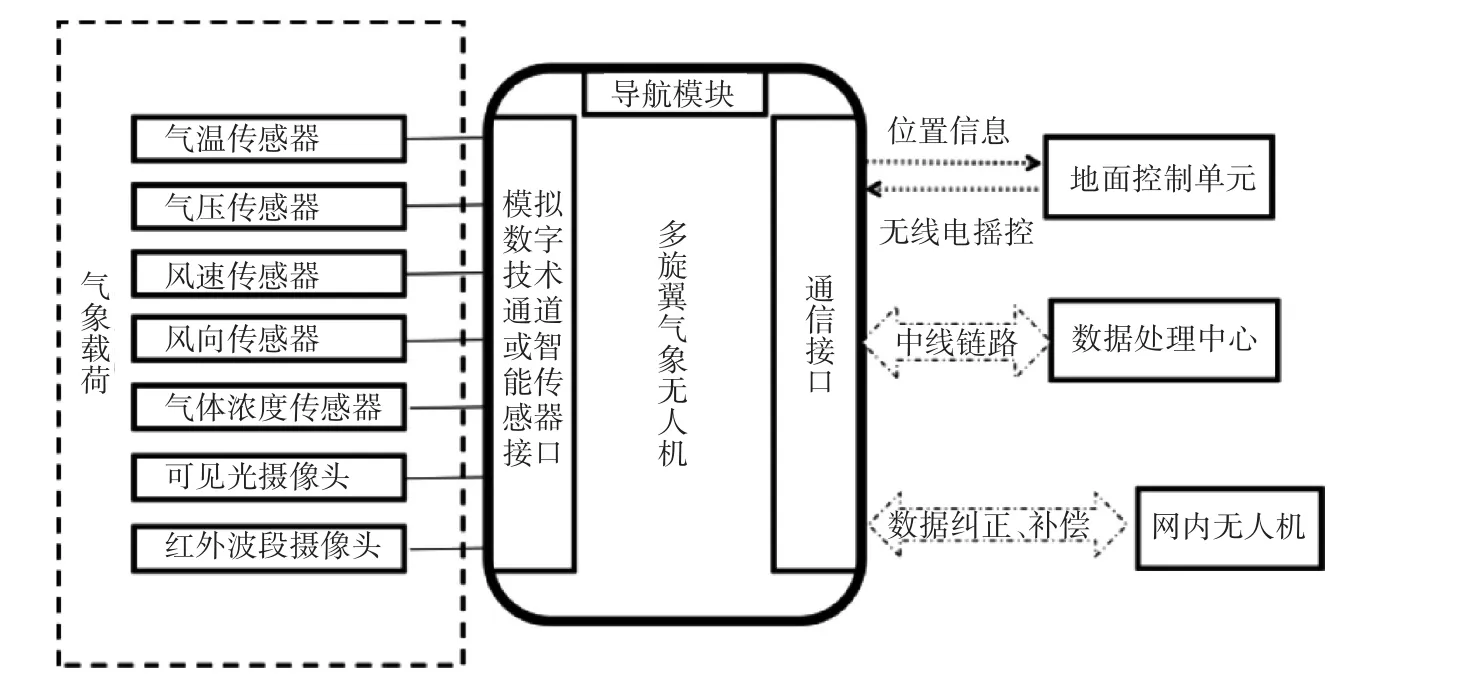
图14 多旋翼气象无人机结构
超声波测风仪一般将两组相互正交的传感器水平安装,每组分别有一个超声波发射器与接收器[11],发射器同时向对向接收器发送声波,由于受风速的影响,接收器收到声波的时间会稍有差异,即顺向和逆向接收到的信号时间存在差值。差值结合超声波传播的速度公式,即可计算风速大小,因此超声波传感器对气体流动较为敏感,其测量数据准确性势必被旋翼产生的风场所影响。
4.2 优化建议
旋翼风场作为影响风探测设备测量准确性的因素之一,为避开其干扰,可首先对无人机旋翼风场进行测量,通过确定其产生风场的平面区域和竖直高度,探测设备的安装区域选择也随即明确。通过本次研究,系统优化方面得出如下几点建议。
1)理论上讲,旋翼数越多,相邻旋翼间距越大,机身距离旋翼距离则越远,中央位置的静风区域越大。对于将测风设备安置于无人机中心正上方一定高度的布局设计,选用六旋翼无人机作为搭载平台为宜。主要出于以下考虑:六旋翼比四旋翼相较,旋翼间距更多,无人机中心正上方给设备预留出的静风区域范围更大;无人机全重及旋翼叶片类型相同情况下,六旋翼无人机旋翼转速比四旋翼转速低,进而对气流的振动强度小。
2)桨叶数目的确定。螺旋桨桨叶越多,桨叶承担的升力越小,转速越低,且在最大拉力相同的前提下,二叶桨直径要比三叶桨直径大。所以螺旋桨叶片数量并非毫无限制,通常选用两叶桨为宜。
3)创新布局结构。通过仿真分析,可知有两处适合探测设备设置的区域:一处是无人机中心位置正上方,缺点是升高了整个测风系统重心;另一处是无人机平台外沿,如图15所示,此种布局优点是不用考虑风的来向,同一时刻有不少于二个传感器不受旋翼风场影响,进而实现对风的准确测量,同时对测得数据进行算术平均,可以使得计算结果进一步契合风场真实信息,缺点是成本增加,且对无人机负载能力要求提高。
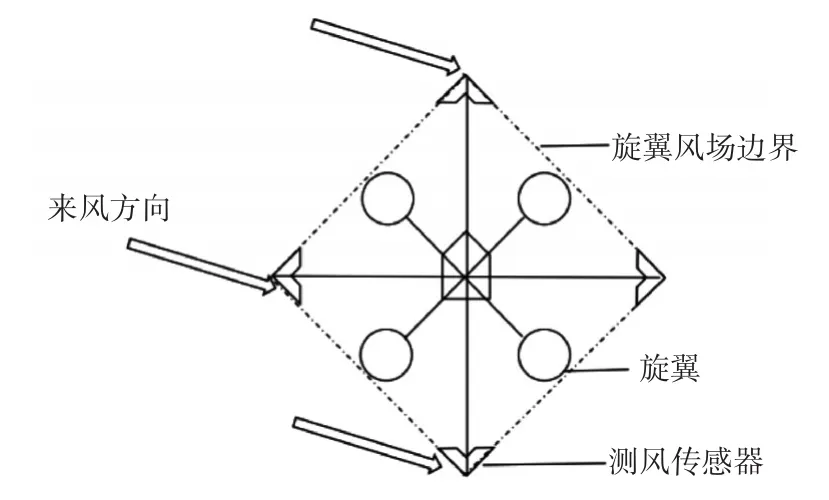
图15 四旋翼无人机多传感器结构设计
5 结语
本文对旋翼无人机旋翼旋转产生的风场进行了模拟仿真,通过对仿真结果的分析摸清了旋翼风场的布局特点,为测风设备/传感器安装提供了指导。
在今后的研究中,可从如下方面着手。
1)研究旋翼在不同转速、不同桨叶外形情况下的流场分布情况,推导旋翼转速、间距比、桨叶外形、桨叶数量等与风场分布之间关联关系,为多旋翼无人机测风系统布局搭建提供更为系统准确的理论支撑。
2)在对流场布局情况深入了解基础上,尝试通过结构设计改变风场流向,如尝试通过在旋翼四周增加隔板方式限制旋翼上方进气范围,进而为测风设备/传感器创造更大配置区域。
3)利用现场实验检测仿真结论的准确性、适用性。
