基于CFDD的柔性飞翼飞行器颤振点分析∗

王民泰 曹云峰 刘海颖 郑维新

（南京航空航天大学航天学院 南京 210016）

1 引言

柔性飞行器具有大展弦比特点，与普通飞行器相比，其优势主要表现为结构简单、重量轻、高空长航时能力及多任务执行能力等。大柔性飞行器有以下三种布局：单翼布局、联接翼布局和飞翼布局。

图1（a）是柔性单翼飞行器［1］，与固定翼飞行器结构类似，但机翼相比较于固定翼飞行器机翼要更加细长。其优点是展弦比大、质量轻；其缺点是机身阻力大，不能完成对灵活性要求较高的任务。

图1（b）是柔性联接翼飞行器［2］，其框架结构是通过后掠前翼与前掠后翼两部分联接组成。其优点是结构强度大、稳定，飞行器框架结构小，更灵活，且飞行速度快；其缺点是在结构、气动弹性、控制方面存在耦合，情况复杂，在控制律设计方面难度较大。

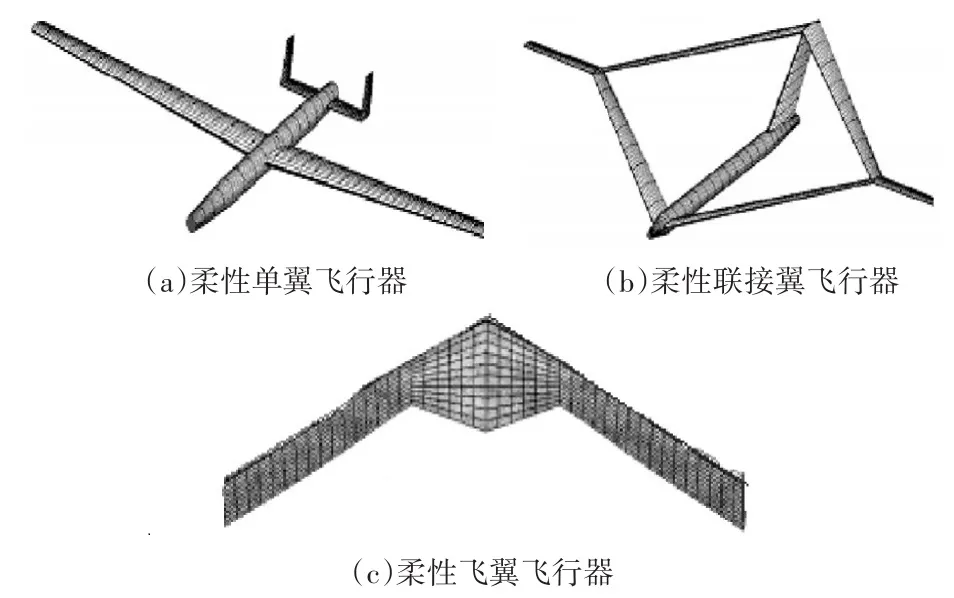
图1 柔性飞行器常见的三种翼型

图1（c）是柔性飞翼飞行器［3］，当前柔性飞行器大多采用这种布局。其优点是飞行器重量小，飞行时受到阻力更小，而且飞行器升力面大，飞行时获得的升力更大。此外，在隐蔽性方面相比较于其他两种布局也有一定的优势；其缺点是飞行器纵向稳定性较差，有发生飞行器静不稳的可能；更重要的是，相比于其他两种柔性飞行器，飞翼布局的结构与气动弹性的耦合性更强，会随着有效载荷的变化而产生大变形。

南昌航空大学的徐江锋［4］通过对柔性飞行器机翼部分建立三维模型，并通过软件CFX对模型进行分析，最后针对机翼的弯曲变形部分进行优化设计，提出了一种可以减少柔性飞行器机翼受气动载荷影响的方案。北京航空航天大学的马铁林［5］通过从流体力学以及结构力学两个方面求解柔性飞行器的气动特性，通过该方法求解发现机翼受到载荷影响变形之后，升阻比减小，气动性影响减弱。

本文着重于地面振动测试的后处理算法，采用一种新型的CFDD估计模态频率和振动模式的形状，并通过正交响应法加以验证。这是建立在明尼苏达大学（UMN）无人飞行器实验室［6～7］以前的工作基础上的，其中的地面振动实验（GVT）是在洛克希德·马丁公司和空军研究实验室开发的机身自由颤振飞行器［8］上进行的。相关的实验（飞行和地面测试）数据、数学模型和飞行软件可在PAAW网站上免费获得。

2 “mAEWing1”号飞行器

洛克希德·马丁公司制造了一系列飞行器。该系列的第一架飞行器被命名为“mAEWing1”［9］，如图2所示。到目前为止，已经设计和建造了两种不同的机体和三种不同柔性的机翼。这架飞行器采用模块化设计，机翼和机体可以分开，可以互换使用。机翼有一个矩形翼梁作为主要的载荷构件。通过用泡沫包裹支撑结构来获得空气动力学形状。有关这些飞机的设计，建造和测试的更多详细信息，请参见文献［9］。

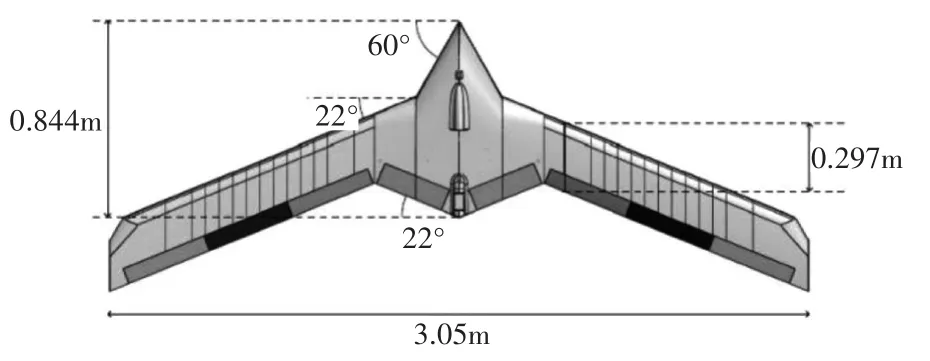
图2 “mAEWing1”号飞行器

3 模态分析

3.1 模型A

模型A的力传感器是用模型粘土安装的。在20个网格点位置进行了10组GVT分析，目标频率范围设置为3Hz～35Hz。使用CFDD和正交响应两种方法分析时域数据，这两种方法在模态频率方面给出了相似的结果，如表1的第1～3列所示。使用两种方法获得的模式形状也是相似的，其中，使用CFDD获得的目标频率范围内的四种模式形状如图3所示。

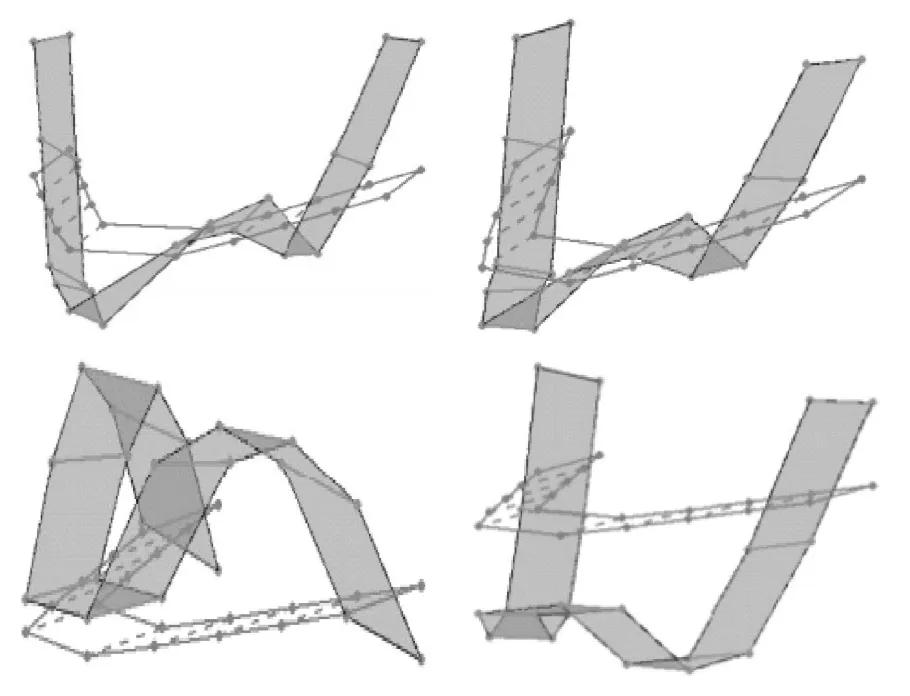
图3 曲线拟合频域分解法产生的模态形状：模型A的第一次模态分析

为了更加细致地观察到噪声对模式形状估计的影响，进行了第二次GVT分析，这次线性调频激发的频率范围被限制在3Hz～13Hz，以更清晰地解析前两种模式形状。表1的第4～5列给出了模态频率，这两个模态都是使用这两种方法从GVT分析中获得的。与第一次GVT分析相比，模态频率只发生了很小的变化。

表1 模型A的模态频率

使用CFDD获得的模式形状如图4所示。可以看出，传导具有较低目标频率范围的GVT有助于降低模式形状中的噪声。

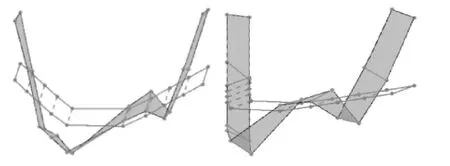
图4 曲线拟合频域分解法产生的模态形状：模型A的第二次模态分析

3.2 模型B

与模型A的配置相比，模型B的装置有一些改进。力传感器通过热熔胶安装在飞机上，与模型A使用粘土底座相比，热熔胶底座更加坚硬。因此，力传递更有效，力测量中的噪音更小，测得的数据更加准确。

对GVT数据应用了CFDD和正交响应两种方法。在3Hz～35Hz的目标频率范围内，CFDD能够识别包括扭转模态在内的5种模态，而正交响应法不能识别其中的弯曲模态（模态2）。表2给出了两种方法识别的模态频率。

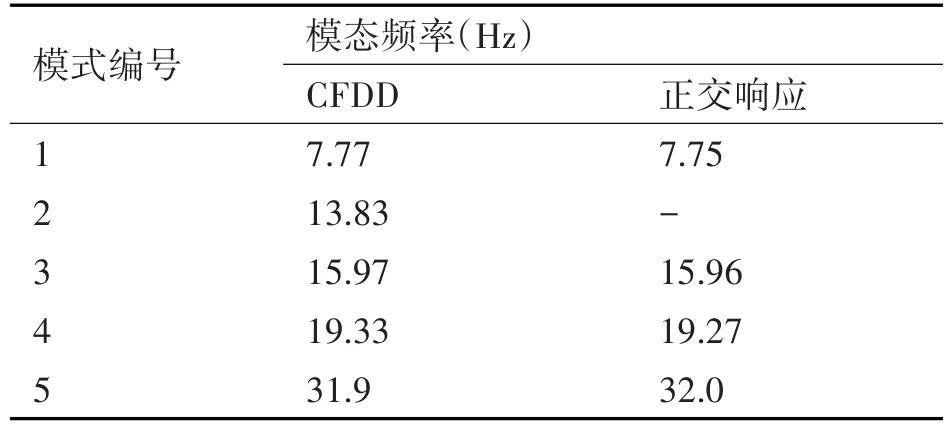
表2 模型B的模态频率

使用CFDD识别的前五种模式形状如图5所示。可以看出，由于在模型B在装置上的改进，与模型A获得的模式形状相比，总体上噪声较小。

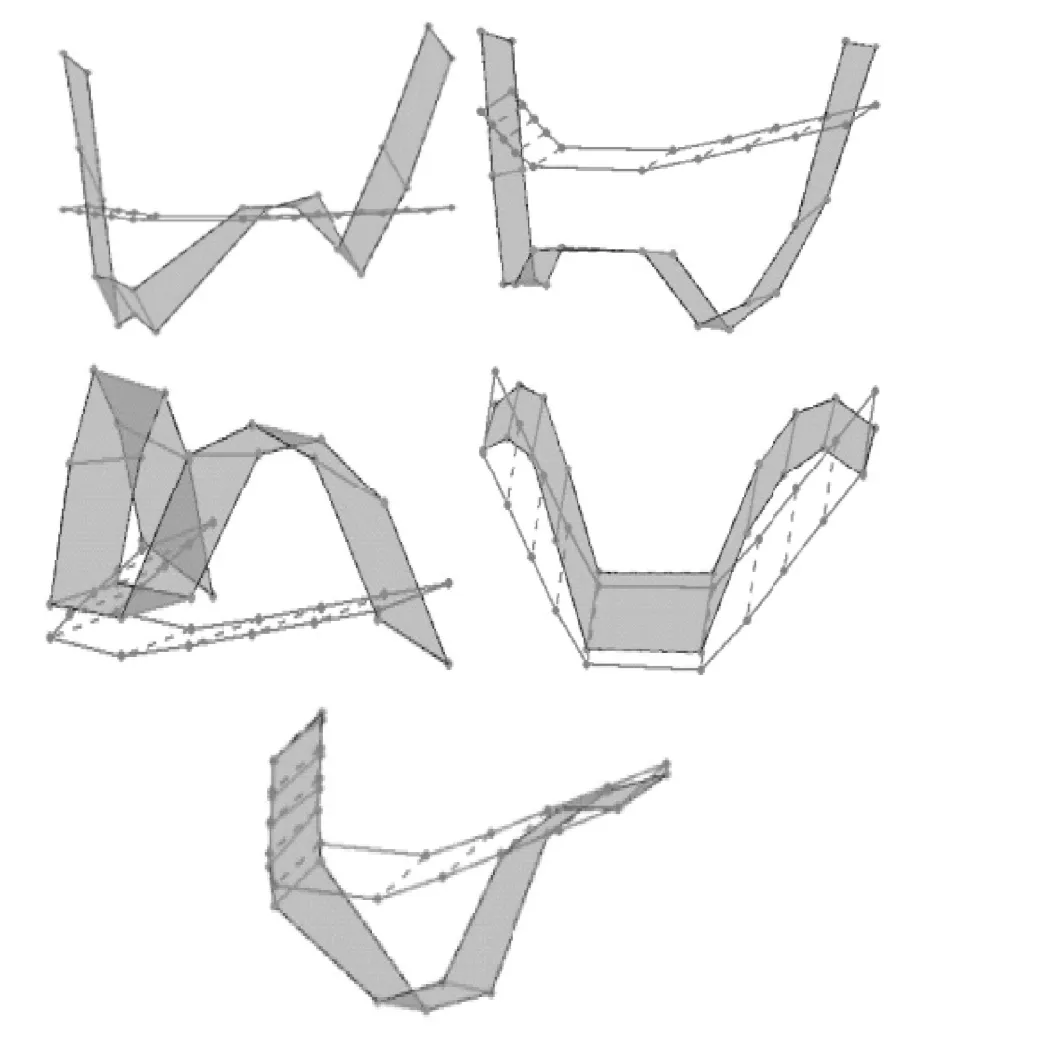
图5 曲线拟合频域分解法产生的模态形状：模型B的模态分析

4 结语

本文提出了一种基于CFDD的柔性飞翼飞行器模态分析方法，并借助UMN无人机实验室在mAEWing1系列飞行器上进行的GVT数据进行模态分析。将通过CFDD所得模态频率与通过正交响应法得出的模态频率进行对比，发现两种方法在对称模态中分析结果相似，而CFDD还适用于非对称、扭转等多种模态。最后本文以动画形式展现出飞行器的模态形状。