水下目标定位自适应相位差估计算法改进研究∗
2021-12-02纪彦星丁贤君
纪彦星 丁贤君
(1.中国人民解放军91404部队 秦皇岛 066001)(2.中国船舶集团有限公司第七〇九研究所 武汉 430205)
1 引言
自适应陷波滤波器(ANF)能够有效地估计和提取背景噪声中的窄带信号参数。早期的研究基于有限脉冲响应(FIR)滤波器和最小均方(LMS)算法。通过采用最陡下降搜索方向,LMS算法具有数值计算复杂度低和鲁棒性强的优点,因此应用比较广泛。为了解决正弦信号的在线频率估计的经典问题,Hsu、Ortega和 Damm[1]提出了一种新的保证全局收敛的ANF。然而,它的主要局限是收敛速度相对较慢,并且对输入相关矩阵特征值扩散的变化敏感[2~3]。为了提高ANF的性能,学者们付诸了大量的研究。Mojiri和 Bakhshai[4]开发了一种改进的ANF,以实现周期性信号的在线频率估计,这种周期信号不必满足正弦条件。此外,他们还证明了该算法具有更简单的稳定性分析特点,即使在纯正弦信号的情况下也减轻了问题的复杂性。梁国龙等[5]提出了频率自跟踪估计器(FATAFE),克服了频率偏差的增加,与自适应频率估计器(AFE)相比,进一步降低了估计偏差和方差。针对宽带噪声干扰下正弦信号的频率估计问题,Punchalard、Lorsawat⁃siri和Loetwassana等[6]提出了二阶自适应FIR陷波滤波器(AFNF)。AFNF的收敛速度和均方误差(MSE)等性能可以很容易地通过步长参数来控制。由于传统的离散化过程在计算自适应滤波器状态导数时会产生偏差,Yoon、Bahn和Lee等[7]提出了一种新的LMS-ANF频率估计的离散导数方法。新的ANF可以准确估计不同频率范围内输入信号的频率。
近年来,采用牛顿搜索方向的递推最小二乘(RLS)算法被引入ANF。这种算法被认为具有更大的应用潜力,受到越来越多的研究。Pei,Tseng[8]提出了一种实时级联ANF来估计正弦信号的振幅、频率和相位(AFP)。Liu,Diniz和Laakso[9]提出了基于复数ANF的抑制射频干扰的方法。此外,刘和胡[10]开发了一种高效的RLS-ANF,用于抑制电力线干扰(PLI)。Paleologu[11]和 Leung[12]还提出了具有可变遗忘因子(VFF)的RLS算法,以实现更少的稳态失调和良好的同步读写能力。但在VFF-RLS算法中需要预先设定的遗忘因子,它们不能很好地跟踪马尔可夫型非平稳过程。因此,通过最小化无噪声后验误差的均方,Bhotto和Antoni⁃ou[13]获得遗忘因子,并提出了一种新的VFF-RLS算法。Zhu等[14]也提出了一种新的基于RLS算法的格型自适应无限脉冲响应(IIR)陷波滤波器,用于估计和跟踪复杂正弦信号的频率。
本文设计了一种基于RLS算法的自适应相移估计器,用来估测有源窄带水声定位系统中阵元间接收信号的相位差。首先介绍了RLS-ANF估计器的结构及其原理,然后对算法进一步改进以解决“跳象限”现象,最后通过仿真和实验进行对比,得出结论。
2 RLS-ANF相位估计器
2.1 波达方向估计
波达方向(DOA)估计是水声定位系统的重要任务之一。在有源窄带定位系统中,其本质都是利用声波到达水听器阵列时的声程差和相移。
如图1所示的一个二元阵系统,阵元间距是d,在远场条件下,平面波到达两个阵元的声程差为
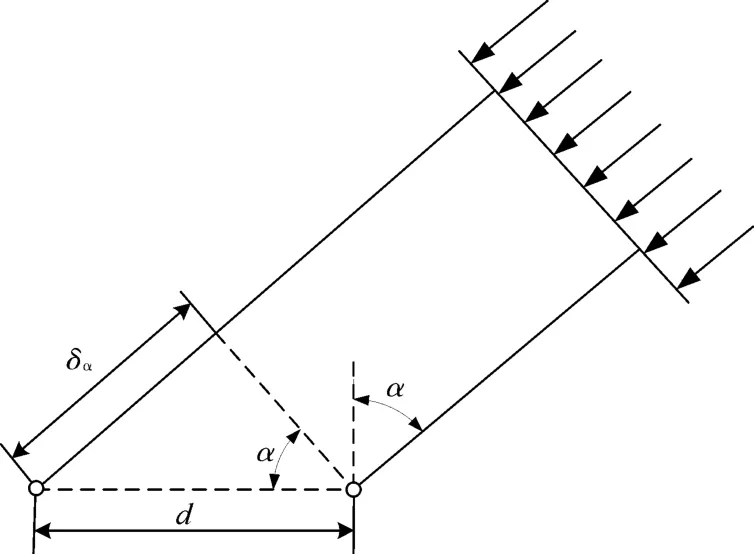
图1 二元阵相位差示意图

其中α是声源的入射角,定义为声线与阵元法线间的夹角。因此相邻阵元接受信号的时延为
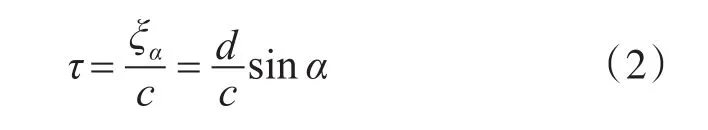
其中c是声音在水中的速度。在窄带有源水声定位系统中,声源的频率ω和波长λ已知。因此,可以得到相邻阵元接受信号的相移:
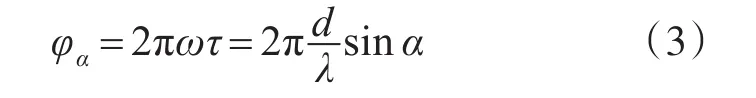
其中α∈(0,±π 2)。式(3)说明相移和入射角一一对应。因此,声源的入射角可以通过测量反应声程差的相移得到。
2.2 RLS-ANF相位估计
为了估计接受信号的相位,在图2中展示了RLS-ANF相位估计器的结构。
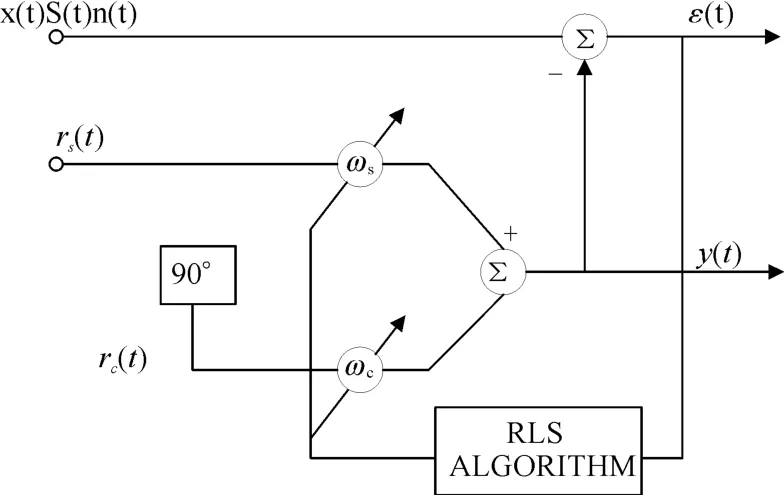
图2 RLS-ANF相位估计器结构图
系统的输入声源和接收声源分别设为
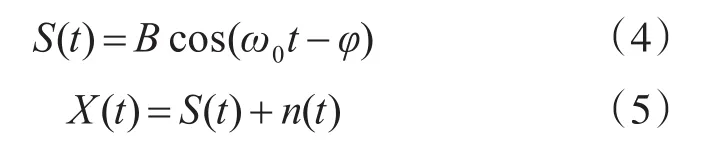
其中n(t)是背景噪声。将两路正交的参考信号rs(t)和rc(t)为
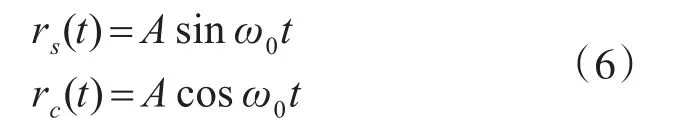
其中ω0与声源的频率相同。参考信号rs(t)和rc(t)的抽头权系数分别为ωs和ωc。因为ANF是维纳滤波器的物理实现,只有当滤波器的频率与声源的中心频率对齐时,才能达到最小均方误差,不然信号会泄露到残差中。
将信号离散化表示,滤波器的输入信号向量为r(n)=[rs(n),rc(n)]T,其对应的抽头权系数为ω(n)=[ωs(n),ωc(n)]T,期望信号为x(n)。滤波器的实际输出是ωn和rn的内积

抽头权系数的递推过程也由Boroujeny,John和Sons[15]推导过。在第N次迭代中,抽头权系数的改变量取决于先验估计误差和增益向量k(n)的内积,增益向量根据各个时刻的采样数据实时更新,这使得RLS算法有更强的适应能力和更敏感的利用新信息的能力。
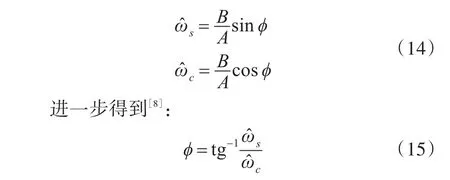
可以证明,由式(15)给出的相位估计器是理想条件下的最大似然比估计器[16]。
3 RLS-ANF相位差估计器
3.1 RLS-ANF相位差估计
在有源窄带定位系统中,重要的待测参数是相位差而不是相位。通过并联两路RLS-ANF相位估计器,可以得到RLS-ANF相位差估计器。
两路估计器对应阵元的期望信号来源于同一个声源,具有相同的频率ω0,只需要一组有着相同频率的rs(t)和rc(t)作为参考信号。RLS-ANF不断利用参考信号的观测数据来更新抽头权系数,然后可分别得到相位估计ϕ1和ϕ2。最终,相位差估计为

3.2 “跳象限”现象
当进行波达方向估计时,需要将两路接收信号的相位差φ12归进区间(-π,π)内。然而大量的仿真证明,当相位差真值φ12接近区间边缘,即±π时,将不可避免地发生“跳象限“现象,这种现象在低信噪比的条件下更容易发生。如图3所示,以下措施可以用来解决“跳象限”现象。
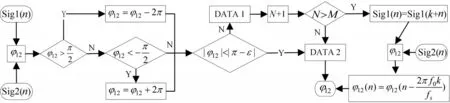
图3 克服“跳象限”现象框图
首先对每个点的相位差估计值进行判决。当满足条件 |φ12|<|π+ε|时,则认为“跳象限“现象会发生,随后这些相位差估计值被存储在DATA 1中,并且记录个数N。剩下的相位估计值存储在DA⁃TA 2中。如果N
4 仿真和实验
4.1 仿真验证
为了验证RLS-ANF相位差估计器的收敛性能,在高斯白噪声的背景下进行了仿真验证。仿真的参数满足以下条件:两路正弦信号的初始相位为-π 4和3π 4,信号的频率ω0为500Hz,采样率fs为3kHz,快拍数为60,SNR为20dB,遗忘因子λ为0.99,抽头权系数的初始值ωs和ωc为0。
RLS-ANF相位估计的收敛曲线如图4所示,图(a)表示绝对误差曲线,图(b)表示抽头权系数的更新曲线。图(a)中的绝对误差在不到20次迭代后就收敛到零附近,随后受噪声影响在一定范围内扰动。当相位绝对误差趋近于零时,图(b)中的抽头权系数快速平稳的收敛。
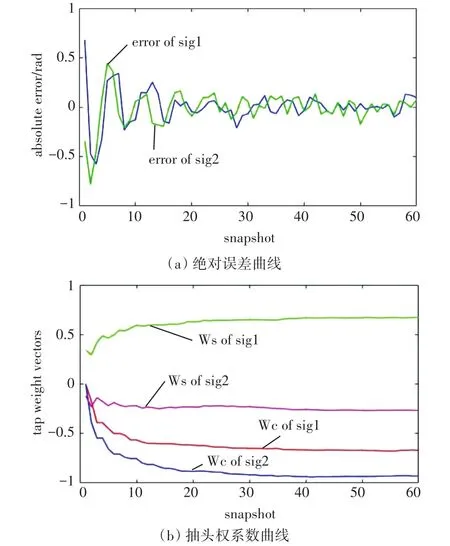
图4 RLS-ANF相位估计器的收敛性能
与此同时,两个信号之间的相位被设置为-π来满足“跳象限”现象。未克服“跳象限”现象的相位差估计曲线如图5(a)所示。可以看到,在某些快拍数上相位差估计值在两个相邻的象限内剧烈跳变,严重影响相位差估计的准确性。利用图3列出的措施克服“跳象限”现象后,得出的相位差估计曲线如图5(b)所示。可以看到,相位差估计值快速收敛到真实值附近,在随后的迭代计算中保持稳定。然后使用蒙特卡洛方法进行500次仿真,平均相对误差低于1‰。因此,使用图3所示的办法来克服“跳象限”现象是非常实用和必要的。
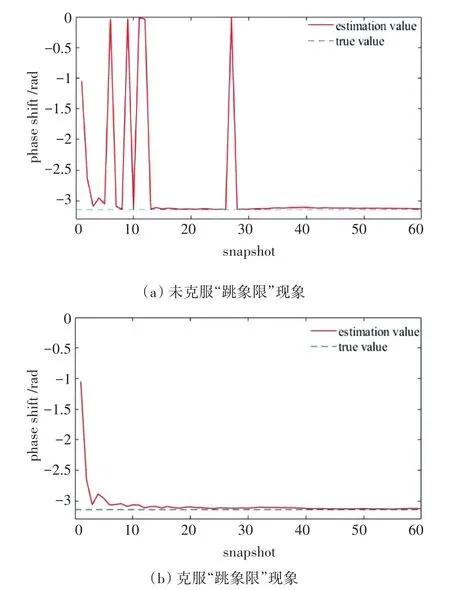
图5 是否克服“跳象限”现象的相位估计曲线
4.2 实验分析
为了满足远场条件,将水听器放置在消声水池进行了声学实验。声源是14kHz的正弦信号,数据采集系统的采样率为108 kHz,相邻水听器接受信号的相位差真实值为π/6。阵元接受到的原始信号如图6(a)所示。对直达声信号进行归一化等预处理后,作为自适应相位差估计器的输入。基阵接收到的两路原始信号和预处理后的信号曲线如图6(b)所示。
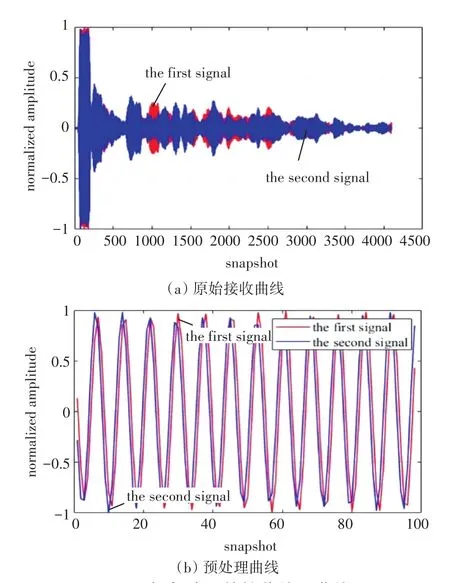
图6 相邻阵元的接收信号曲线
为了对比两个相位差估计器的性能,同时使用LMS-ANF和RLS-ANF来计算处理后的信号。RLS-ANF的遗忘因子为0.99,LMS-ANF的步长参数为0.002,两个相位差估计器的中心频率都和声源相同,其他参数保持一致。LMS-ANF的相位差估计曲线如图7(a)所示,相位差估计值在30次迭代计算后渐渐收敛到真实值附近,随后在稍微大的范围内上下浮动。RLS-ANF的相位差估计曲线如图7(b)所示,很明显,相位差估计曲线在更短的时间内就收敛到真实值附近,并在随后的迭代计算中保持稳定。因此,两种估计器都能对环境有很好的适应能力,并以较高的精度完成相位差估计,但是,RLS-ANF比LMS-ANF需要更少的快拍数,并且具有更强的抗干扰能力。
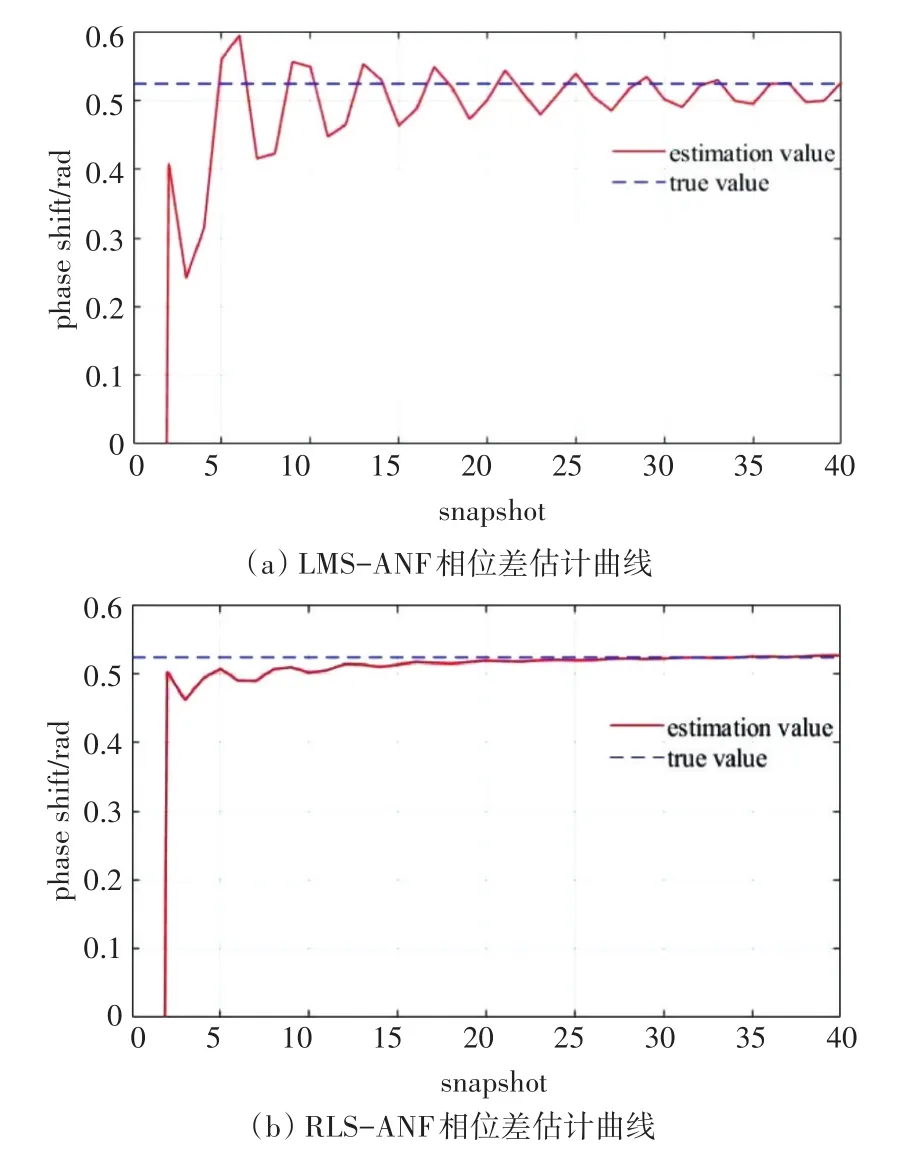
图7 两种估计器的相位差估计曲线
5 结语
本文提出了一种基于RLS算法的自适应相移估计器。针对“跳象限”现象,进一步改进了RLS-ANF。改进算法的有效性通过仿真得到了验证。并且,通过实验将LMS-ANF和RLS-ANF进行了性能对比。结果显示,RLS-ANF有更快的收敛速度,更强的抗干扰能力,更好的稳定性,也更适合主动式窄带定位系统的实时应用。
