装甲车辆汇流行星排动力学建模与仿真分析

田钦文，冯辅周，王子涵，陈晓明

(1.陆军装甲兵学院， 北京 100057； 2.PLA No.96784部队)

1 引言

综合传动装置是以机械变速机构为基础的新型传动装置，是我军新一代履带式装甲底盘推进系统的重要组成部分。汇流行星排是一种典型的行星齿轮传动系统，是传动系统的部件之一。汇流行星排位处变速箱箱体两侧，通过连接轴与侧减速器相连，如图1所示。变速机构和转向机构的动力经汇流行星排汇流后，驱动车辆直驶和转向。

一般情况下，在汇流行星排的故障早期，车辆驾驶人员难以直接感受故障带来的车辆操纵或振动及噪声的明显变化。由于汇流排的主要功能为汇流直驶和转向功率，故障发展到一定程度会造成车辆无法转向或转向失灵，这给车辆在作战使用中带来了极大的隐患。国内外学者针对汇流行星排的动力学问题进行了大量研究。刘修骥[1]研究了履带车辆汇流排双流变速箱外制动条件下的汇流行星排特性参数求解；李军等[2]通过固有频率及振型特点对大半径转向条件下汇流行星排振动模式进行了对比分类，分析了不同行星轮轴承刚度下接触力频谱特性；冯国飞[3]研究了综合传动中汇流行星排在不同工况条件下载荷特性的变化，并对其失效情况进行了分析；冯辅周[4-7]课题组采用深度学习等一系列方法寻找汇流行星排故障特征分析的最优解。本文通过建立汇流行星排刚柔耦合模型，对比行星齿轮不同程度裂纹的仿真接触力信号、箱体表面测点加速度信号，分析裂纹程度加深时所表现的故障信号特性。

1 综合传动装置汇流行星排布置示意图

2 汇流行星排的结构及工作原理

如图2所示，综合传动汇流行星排主要由行星轮系与定轴轮系组成。其直驶动力通过输入轴1将动力传递给齿轮1输入到齿轮2，转向动力由输入轴2传递到太阳轮输入。两路动力经行星轮汇流后从行星架输出。当固定太阳轮，即仅从输入轴1输入动力时，齿轮1将动力传递到齿轮2，输出速度等同输入速度；当输入轴1与输入轴2同时输入动力时，齿轮2与行星轮差动，输出速度不同输入速度。本文采用固定输入轴2，给输入轴1动力的方式进行研究。

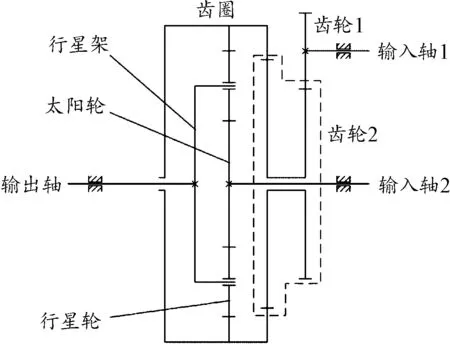
图2 汇流行星排简图

3 汇流行星排的刚柔耦合建模

根据图3所示思路，建立汇流行星排刚柔耦合模型：

图3 汇流行星排刚柔耦合建模思路框图

根据表1基本参数，运用Solidworks软件绘制单个零件实体模型，进行干涉检查，保证各零件的正确位置及初始形态，添加配合关系将单个零件构成三维实体模型。

表1 汇流行星排主要部件基本参数

ADAMS可根据已有实体自动柔性体，但是其网格划分简单，单元类型单一，难以达到仿真分析要求，因此通过ANSYS建立柔性体模型，在ADAMS中读取之后删去原有部件，构建刚柔耦合模型。

在ANSYS中建立箱体及行星轮有限元模型如图4所示。

图4 箱体及行星轮有限元模型示意图

在ADAMS中分别导入柔性化的箱体与行星轮替换原有实体，重新构建柔性连接并激活。最终建立汇流行星排刚柔耦合模型如图5所示。

图5 汇流行星排刚柔耦合模型示意图

3 刚柔耦合模型的验证

齿轮传动系统动力学模型一般通过各部分仿真角速度信号与理论数值验证动力学模型的准确性[8]，在仿真角速度平均值符合理论值的条件下，其传动比也符合理论值，在ADAMS软件中则反映为运动副与接触力设置的正确性。根据转化机构法[9]计算汇流行星排主要传动部件的转频及啮合频率，如图6所示。以行星架为动参考系，行星系统中各部件之间的相对运动关系仍保持不变，可视作定轴轮系求解角速度。

图6 转化机构示意图

(1)

则两部件之间相对于行星架的传动比为：

(2)

其中Z1、Z2、Z3分别为太阳轮齿数、行星轮齿数、齿圈齿数。

行星轮系运转过程中，太阳轮与行星轮、行星轮与齿圈的啮合点具有相同的线速度：

(3)

即：

|f1-fH|×Z1=|f2-fH|×Z2=|f3-fH|×Z3

(4)

式中f1、f2、f3、fH分别为太阳轮转频、行星轮转频、齿圈转频及行星架转频。

平稳工况下，在汇流行星排的输入轴1上施加逆时针方向的直驶驱动转速1 200 r/min(20 r/s)，在输入轴2上施加顺时针方向的转向驱动转速600 r/min(10 r/s),根据上述传动原理及齿轮参数，计算得到各部件理论转速如表2所示。

表2 汇流行星排理论转速

则汇流行星排的啮合频率：

fm=|f1-fH|×Z1=|f2-fH|×Z2=

|f3-fH|×Z3=254.27 Hz

设定仿真时长1 s，仿真步数3 000步，得到主要部件角速度仿真信号曲线如图7，图中各部件角速度平均值见表3。

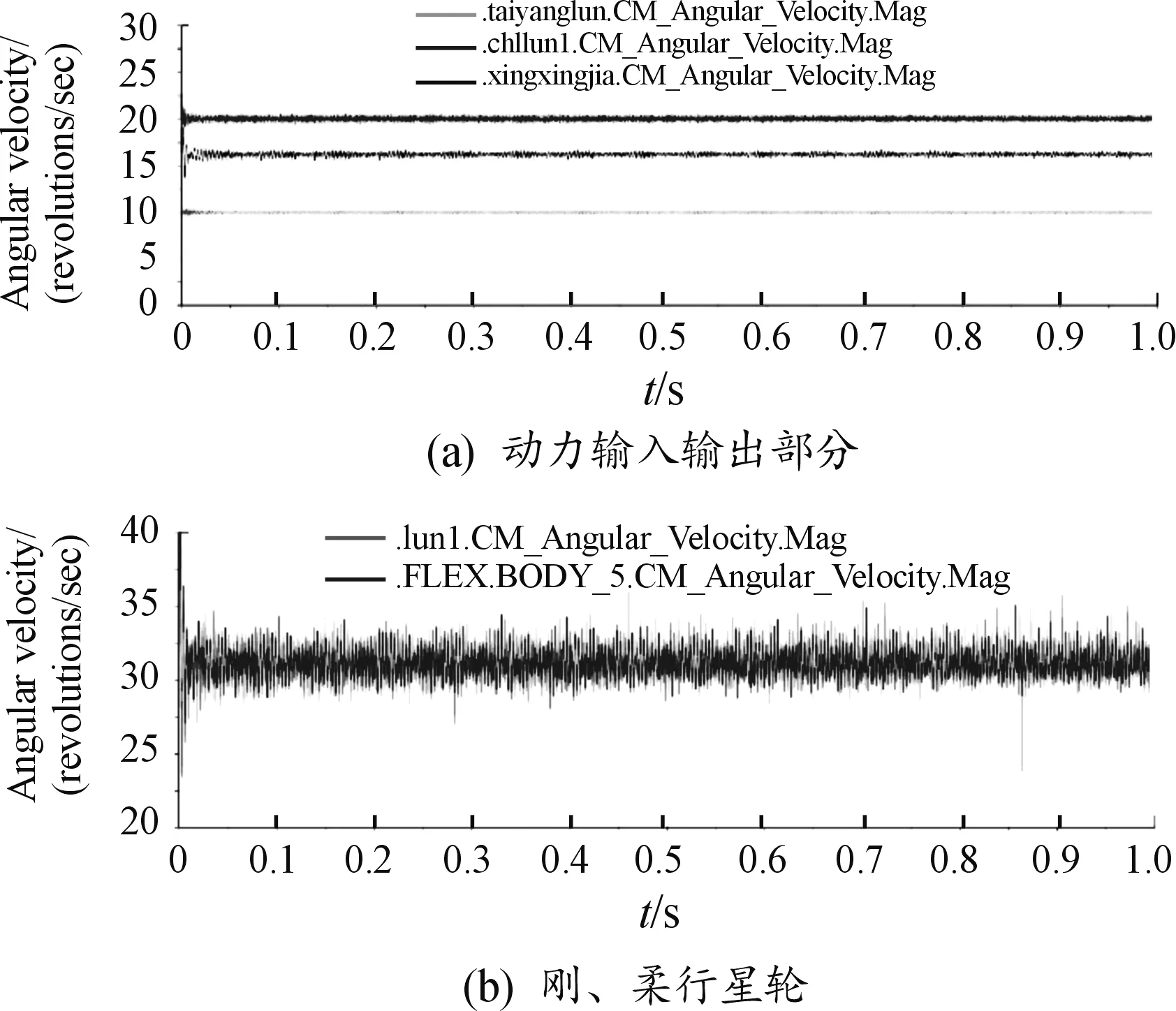
图7 主要部件角速度仿真信号曲线

表3 主要部件仿真角速度平均值

从图7与表3可知，仿真初始状态各部件角速度均存在一定程度波动，稳定后各部件仿真角速度信号平均值基本与理论值相同，说明动力学模型约束与接触设置正确，符合实际传动关系。行星轮仿真角速度信号波动幅度较大，这是因为三维建模及几何装配时存在一定的模型误差及装配误差，加上摩擦阻力及柔性体形变的影响所致。柔性体行星轮角度波动比刚体行星轮剧烈，而仿真角速度平均值小于刚体行星轮，说明仿真过程中柔性体行星轮与齿圈、太阳轮啮合时发生形变，齿面接触时间较刚体行星轮更长，导致齿轮运行时角速度变化较大，而角速度平均值较低。相较之下，柔性体模型的特征响应更为明显，对行星轮进行柔性化处理更科学合理。

选取箱体表面两个测点(测点1靠近输入轴1，测点2靠近输入轴2)加速度信号进行分析，以验证箱体与传动系统柔性连接的准确性。取垂直于箱体表面方向仿真加速度信号，并通过FFT分析其频谱成分，其曲线如图8、图9所示。

图8 仿真加速度时域信号曲线

从图8、图9可知，两个测点都包含了定轴部分频率960 Hz及其倍频、行星排啮合频率254.5 Hz及其倍频，在行星排啮合频率基频及二倍频附近出现逐渐衰减的边频带；测点2相对于测点1波动更为剧烈，在频域上的特征响应更加明显，这是因为行星排至测点2的振动传递路径更短、距离测点2更近，而测点1更靠近定轴部分，定轴部分频率及其倍频更为明显。仿真加速度时域、频域信号表明，柔性处理后的箱体与传动轮系的柔性连接设置正确，能够反映其振动特性。

图9 仿真加速度频域信号曲线

4 不同程度裂纹故障特性仿真及结论

为模拟行星齿轮单个齿轮的单个轮齿不同程度裂纹故障，在Solidworks中对行星齿轮实体模型添加拉伸切除特征。在齿轮啮合过程中，行星齿轮齿根部位在反复出现应力极大值处易产生裂纹，且会在应力变化下不断加深裂纹。如图10所示。

图10 齿根裂纹示意图

行星齿轮不同程度裂纹故障模拟如图11所示，图中M为裂纹初始位置，为裂纹方向与齿轮中线夹角，以MA段长度段占MB段长度的百分比表示齿根裂纹的损伤程度，分别在裂纹程度20%、50%、100%时对行星齿轮进行特征添加，并导入汇流行星排刚柔耦合模型进行动力学分析。

图11 行星齿轮裂纹故障模拟示意图

将输入轴2固定，在输入轴1施加驱动1 500 r/min，设定仿真时长1 s，步数3 000。此时汇流行星排主要频率成分有定轴部分频率1 200 Hz、行星排啮合频率662.56 Hz、行星齿轮局部故障频率39 Hz。保持仿真工况不变，分别对行星齿轮正常状态、20%裂纹、50%裂纹、100%裂纹局部故障进行仿真分析，仿真得到的接触力时域、频域波形曲线分别见图12、图13。

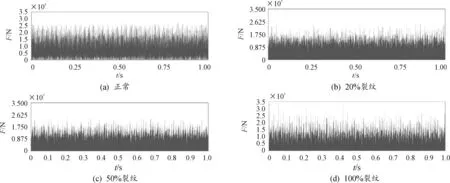
图12 仿真接触力时域信号曲线

图13 仿真接触力频域信号曲线

对比图12(a)、(b)，图13(a)、(b)可知，在时域上，行星齿轮正常状态下接触力信号较为平稳，整体幅值较高，发生裂纹故障时，接触力周期性冲击更加明显，波动范围较大，且接触力幅值较低。仿真接触力信号是对齿轮啮合刚度的直观体现，齿轮在单双齿交替啮合过程中发生啮合刚度突变，导致接触力出现周期性冲击，当齿轮发生局部裂纹故障时，齿轮啮合刚度变化更为剧烈，因此周期性冲击更加明显。同时，由于裂纹改变了齿根处局部截面的惯性矩，引起弯曲刚度、拉伸刚度和剪切刚度的下降，齿轮的时变啮合刚度下降，所以发生裂纹故障时接触力信号幅值低于正常状态。

在频域上，两者的主要特征频率皆为662.5 Hz为基频及其倍频的行星排啮合频率，且啮合频率及其倍频两侧都出现了频率间隔为39 Hz的边频带。相比之下，发生裂纹故障时在低频段出现39 Hz的行星齿轮局部故障频率，且其各次倍频较为清晰，而正常状态下低频段频率成分较为模糊；裂纹故障发生时啮合频率两侧边频带更加明显，呈现出逐渐衰减趋势。

通过仿真得到表4数据，可以看出随着裂纹程度的加深，仿真接触力信号均值逐渐下降，即裂纹越深，齿轮啮合刚度越低；而接触力均方根值逐步上升，说明裂纹程度越高，齿轮发生变形产生的接触力波动越强。

接触力信号在工程实际中难以获得，因此在实际的汇流排状态信号采集过程中，常将振动传感器置于固定的齿圈上或箱体表面，通过获取振动加速度信号并结合进一步的信号分析处理方法来判断部件状态。提取动力输出端靠近轴承部分箱体表面测点仿真加速度信号进行分析，如图14所示。

从图14可知，正常状态时仿真加速度信号较平稳，波动范围较小，而发生裂纹故障时加速度信号波动范围较大，且出现了明显的振动冲击。随着裂纹程度增加，仿真加速度信号无明显差别，需要进一步分析其频域信号，如图15所示。

表4 不同程度裂纹时域仿真接触力信号均值与均方根值(N)

图14 仿真加速度时域信号曲线

图15 仿真加速度频域信号曲线

从图15可知，在频域上，两者都体现了定轴部分特征频率1 200 Hz及各次倍频、行星排啮合频率662.56 Hz及各次倍频，在啮合频率附近出现逐渐衰减的边频成分。裂纹产生时，由于故障频率的调制作用，行星排啮合频率两侧以39 Hz为间距的边频带更为明显，边频带能量明显增加，且在低频段出现了39 Hz及其各次倍频的故障特征频率。而正常状态下啮合频率两侧边频带模糊，幅值较低。

5 结论

1) 在时域上，随着裂纹加深，仿真接触力信号均值逐渐下降，齿轮裂纹深度与啮合刚度呈反比趋势，即裂纹越深，齿轮啮合刚度越低；接触力均方根值逐步上升，说明裂纹程度越深，齿轮变形产生的接触力波动越强。在频域上，随着裂纹加深，低频段行星齿轮局部故障特征频率及其倍频幅值有明显提升，行星排啮合频率幅值有所下降而边频峰值上升。

2) 随着裂纹的加深，低频段故障特征频率的幅值有所提升，行星排啮合频率的幅值有所下降，边频带能量提升。同时由于定轴部分特征频率及振动传递路径的影响，加速度频谱图频率成分复杂，与接触力信号相比不易识别。