联合多核FCM和改进GOA的多无人机协同侦查航迹规划

靳江锋，刘 旭

(中国飞行试验研究院， 西安 710089)

1 引言

无人机(unmanned aerial vehicles，UAV)凭借成本低、适应性强、零伤亡等特点，在民用和军用领域发挥着越来越重要的作用[1]。航迹规划作为无人机任务规划的核心部分，目前在有效规避障碍和威胁的飞行航迹研究方面已经相当成熟，出现了大量静态、动态、二维与三维规划算法[2-4]，但是，针对侦查大规模目标多无人机协同航迹规划的研究还相对较少，特别是，面对大规模协同航迹规划问题，提升侦查效率、突出侦查针对性和有效性是亟需解决的难题。

多无人机协同侦查航迹规划需要考虑的约束条件多且模型复杂，求解效率直接决定了协同侦查效率。序列凸优化(sequential convex programming，SCP)方法近年来受到关注[5]，研究表明，SCP具有更强的高维复杂求解能力，但是存在运算时间长的缺陷[6]。利用群智能优化算法较为突出的运算性能，对协同侦查模型进行快速最优化求解是当前研究的热点。文献[7]将改进遗传算法引入到航迹规划求解中，提高了航迹规划精度。但面对复杂高维优化问题，智能优化算法易陷入局部极值和求解精度不高的缺陷需进一步研究，这也是本文研究的重点内容之一。此外，文献[8]采用模糊C均值(Fuzzy C-means，FCM)对目标进行聚类分析，从而得到每架无人机最佳攻击序列，提高了攻击的针对性，但是该方法受聚类算法性能的影响较大。文献[9]综合考虑任务时间约束和攻击约束，集中一体化求解无人机航迹，一定程度提高了协同航迹规划的有效性，但是该方法数据处理维度较高，运算效率较低。文献[10]将多无人机协同侦察航迹规划等效为多旅行商问题，从而得到了可行飞行航迹，但是该方法更适用于小规模侦查目标应用场景。

为此，本文从侦查任务需求出发，提出一种联合多核FCM和改进蝗虫优化算法(grasshopper optimization algorithm，GOA)的多无人机协同侦查航迹规划算法：采用改进的多核FCM对多类型侦查目标进行聚类分析，根据聚类结果分别派出匹配度更高的无人机执行侦查任务；综合研判无人机航迹规划约束条件，建立基于时间代价的最优航迹规划目标函数；采用改进的GOA对目标函数进行求解，通过重新定义蝗虫编码和迭代更新方式，进而得到每架无人机侦查序列。该方法更侧重于研究新的多无人机协同侦查模式，以提供更适用于实际应用的多无人机协同侦查航迹规划方案。

2 侦查目标聚类分析

以多无人机对目标执行照相侦察任务为例，设有N架具备不同侦查能力的无人机，需要对M个目标进行侦查，第i个目标Ti(Tri,Pri,Imi,Coi)相关信息已知(Tri为威胁度、Pri为优先级、Imi为重要程度、Coi为覆盖面积)。采用模糊聚类技术对目标进行聚类分析，以提高目标侦查的针对性和任务完成的可靠性。

2.1 多核FCM

FCM是目前应用最为广泛的模糊聚类算法之一，但是仅适用于样本均衡的聚类分析场景[11]。为此，部分学者利用高维映射函数Φ(Tk)，将传统FCM的欧式距离转换为高维空间的线性距离，即：

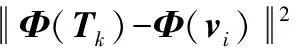
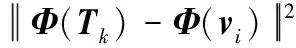
ΦT(Tk)Φ(Tk)-ΦT(Tk)Φ(vi)-Φ(Tk)ΦT(vi)+ΦT(vi)Φ(vi)

当ΦT(Tk)Φ(vi)满足Mercer条件[12]时，不需要知道Φ(Tk)具体形式就可以实现聚类分析，此时称ΦT(Tk)Φ(vi)为核函数，而且任何半正定的函数都可以作为核函数。

为提升对大规模且孤立点较多、维度较高数据的聚类性能，设计多核FCM，即采用Q个Φj(Tk)对Tk进行高维映射：

Θ(Tk)=η1Φ1(Tk)+…+ηjΦj(Tk)+…+ηQΦQ(Tk)

其中，ηj为权重系数，且η1+…+ηQ=1。为便于范数计算，引入多核矩阵AQ×Q：

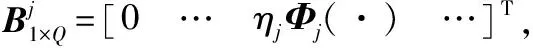
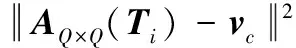
(1)

将式(1)代入J(U,V)有：

下面给出μic、vc和D(Ti,vc)计算推导过程：

1)μic计算

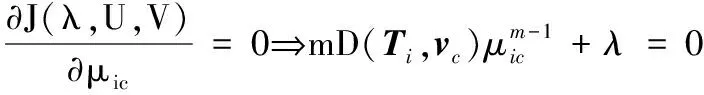
2)vc计算

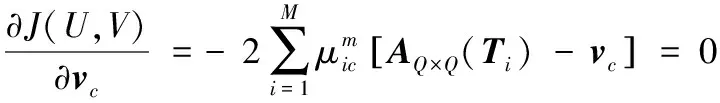
3)D(Ti,vc)计算

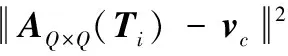
(A(Ti)-vc)T(A(Ti)-vc)=

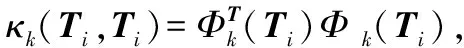
其中，κk(Ti,Ti)为核函数。从μic、vc和D(Ti,vc)的推导过程可以看出，给定Q个满足Mercer条件的核函数就可以实现多核FCM聚类分析。

2.2 基于多核FCM的侦查目标聚类分析

多核FCM引入了多个高维映射函数，提高了复杂数据聚类分析能力，但是仍然存在缺陷：容易陷入局部极值；对初始聚类中心敏感；聚类个数C需要事先已知。为此将GOA[13]引入到多核FCM迭代聚类过程，即将聚类中心V={v1,…,vC}等效为蝗虫个体编码，J(U,V)等效为GOA目标函数，通过GOA不断迭代进化，最终实现聚类分析，可有效克服容易陷入局部极值和对初始聚类中心敏感的缺陷。此时，在每次GOA迭代过程中，vc为某个确定的向量，省略了vc计算过程，故D(Ti,vc)可以简化为：

D(Ti,vc)=‖A(Ti)-vc‖2=

(A(Ti)-vc)T(A(Ti)-vc)=

(2)

(3)

(4)

为解决C需事先已知的问题，设置C在[Cmin,Cmax]范围内依次变化，分别执行GOA操作，选取使得J(U,V)取值最小时对应的聚类个数为最佳Cbest。

基于多核FCM的目标聚类伪代码如下：

输入：目标集；核函数；GOA初始设置

输出：目标聚类结果

begin

C←Cmin

whileC≤Cmaxdo //GOA操作

t←1

fort≤Tmaxdo

w←1

forw≤Odo //O为GOA种群个数

根据式(2)～式(4)计算蝗虫个体目标函数值

执行GOA更新操作

end for

更新种群信息

end for

比对J(U,V)取值，保留最小值及对应的聚类个数

end

C←C+1

end

3 多无人机协同侦查航迹规划

采用改进的多核FCM对侦查目标聚类分析，得到C个目标子类：

根据子类目标属性，合理派出N架无人机执行协同侦查任务。为方便问题描述且不失一般性，取N=C，并设定每个Sui只对应一架无人机Uj(1≤j≤C)。为尽可能降低侦查时间、减少无人机损伤和提高侦查成功率，采用改进的离散蝗虫优化算法(Improved Discrete GOA,IDGOA)对Uj航迹点进行规划。

3.1 代价函数

选取UAV执行任务消耗时间作为代价函数，对于Uj，执行对Sui的侦查任务，Uj按照一定顺序先后完成对Sui内Mi个目标的侦查任务，消耗时间为

设定整体任务时间最小为协同规划目标函数，并采用IDGOA对UAV航迹进行优化求解，从而得到最佳航迹路线。

3.2 IDGOA优化航迹实现

GOA作为最近被提出的新型智能优化算法，在连续优化领域展现出突出的寻优性能[14]。为使GOA能够应用于航迹规划问题，提出改进离散GOA(IDGOA)：重新定义多段式蝗虫个体编码，设计多种进化更新策略。

个体编码对于蝗虫个体Xi(t)，定义其编码为

(5)

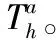
图1 个体编码示意图

更新策略从个体编码定义可以看出，如果仍采用基本GOA进化更新操作，会产生大量无效解，为此提出自适应交换、自适应学习和突变3种更新策略。

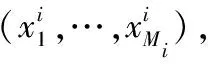
其中，ηi，max、ηi，min为ηi最大和最小值，Tmax为最大迭代次数。图2为自适应交换操作示意图。

图2 自适应交换操作示意图

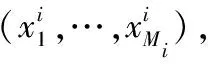
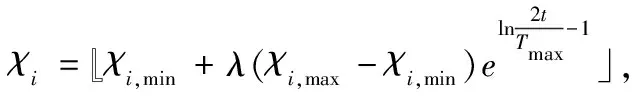
1<χi,min≤χi≤χi,max≤α

其中，χi,min、χi,max为χi最小和最大值，图3为自适应学习操作示意图。

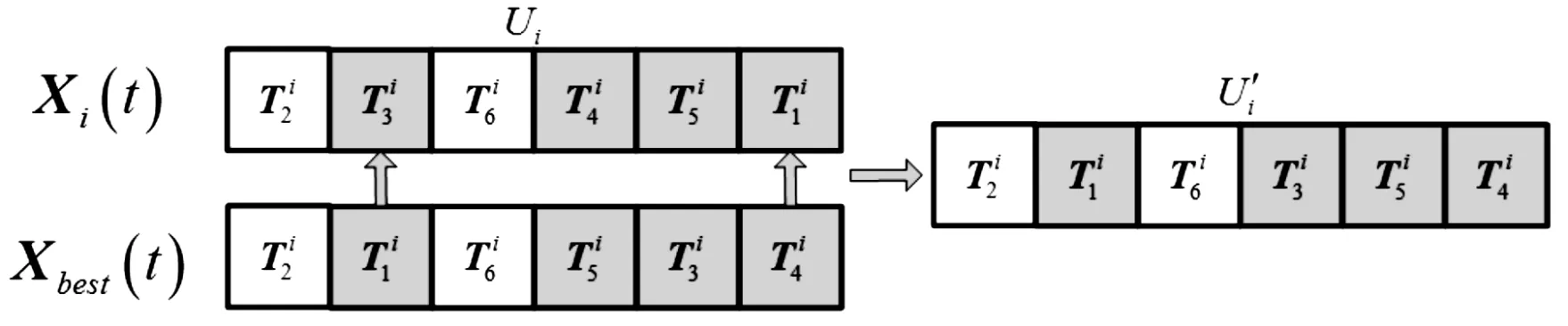
图3 自适应学习操作示意图

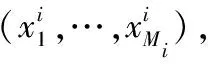
图4为突变操作示意图。

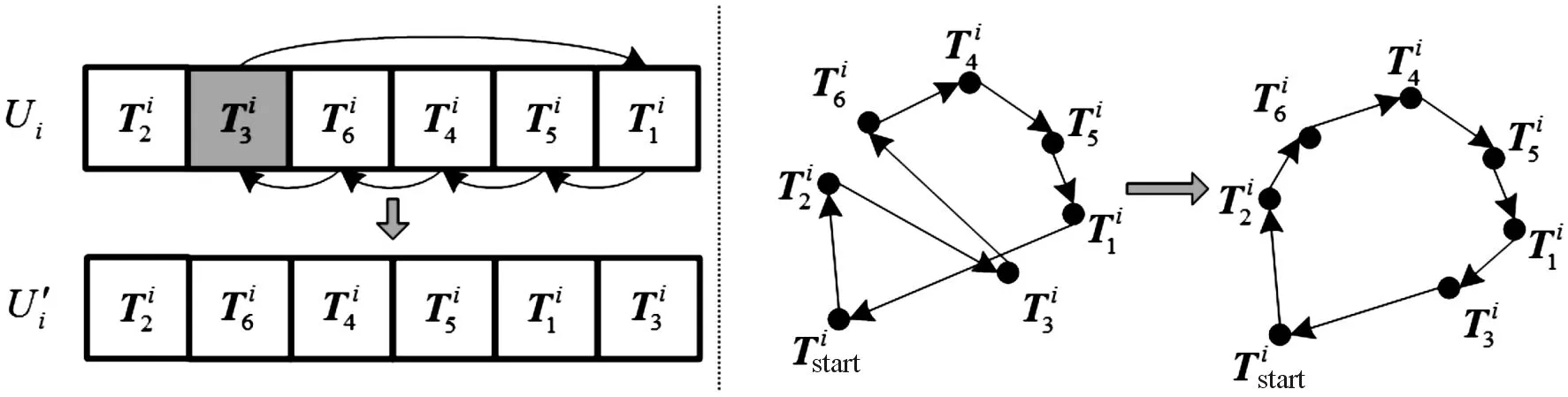
图4 突变操作示意图Fig.4 The schematic diagram of mutation operation

从上述3种进化策略可以看出，随着迭代次数不断增加，蝗虫个体参与“自适应操作”的编码不断减少，而从优秀个体得到的信息不断增加，并且采用突变操作，有效扩展算法的收敛空间，提升收敛效率。给出IDGOA个体编码和更新策略后，将时间代价函数定义为IDGOA目标函数，通过迭代更新，得到每架无人机航迹点信息，最终得到协同侦查航迹路线。

基于IDGOA的多无人机协同侦查航迹规划实现伪代码如下：

输入：无人机参数；目标分类；无人机与目标子类对应关系；IDGOA初始设置

输出：协同侦查航迹

begin

根据个体编码定义，对蝗虫种群进行初始化

t←1

whilet≤Tmaxdo

fori≤PGOAdo //PGOA为种群规模

对Xi(t)所有编码片段执行自适应交换操作

end

更新种群信息

fori≤PGOAdo

对Xi(t)所有编码片段执行自适应学习操作

end

更新种群信息

if(种群进化停滞) do

对种群最优解执行突变操作

end if

更新种群信息

t←t+1

end while

end

计算复杂度根据IDGOA实现流程，设种群初始化计算复杂度为O(PGOAM)，每次迭代最大计算复杂度为O((2PGOA+1)M)，可得IDGOA计算复杂度为

Tmax×O((2PGOA+1)M)+O(PGOAM)≈TmaxO(2PGOAM)

4 仿真实验

仿真实验分为两个部分：多核FCM性能验证实验和多无人机协同侦查航迹规划实验。表1表示了无人机参数设置，其中，V为无人机速度、R侦查半径、(x,y)为空间坐标位置。表2表示了改进GOA参数设置，其中，Q为种群规模、λ为控制系数。

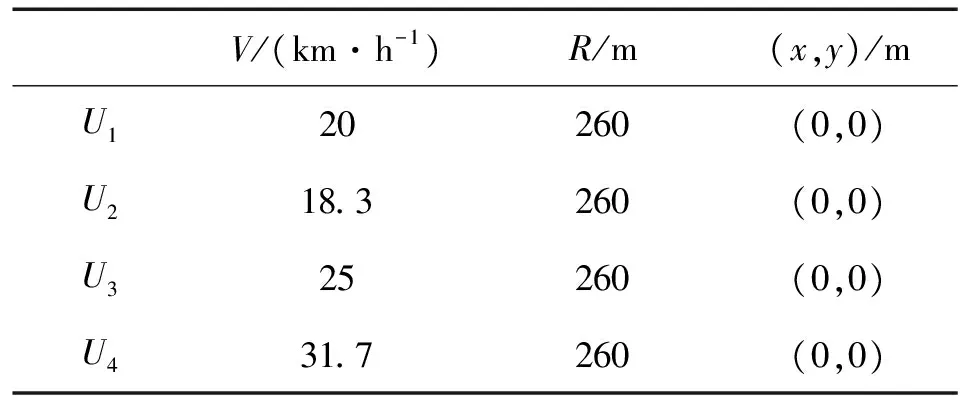
表1 无人机参数设置

表2 改进GOA参数设置

4.1 多核FCM性能验证

采用经典的Nursery数据集、Adult数据集以及人造数据集对多核FCM聚类性能进行验证，并选取基本FCM、核主元熵FCM[15]进行对比实验，假定人造数据集聚类个数对3种算法是未知的。每种算法独立运行30次，对于人造数据集，定义聚类评价指标EC：

EC反映了不同类之间的离散度，EC取值越小，表明聚类效果越好。表3给出了不同数据集下各评价指标对比结果，其中EC,i/EC,j表示FCM、核主元熵FCMEC取值与本文提出多核FCMEC取值的比值。

从表3可以看出：对于数据规模较小的Nursery数据集，多核FCM与核主元熵FCM都展现出了很好的聚类性能，聚类正确率都在90%以上，而FCM聚类正确率只有56.6%。对于较大规模Adult数据集，多核FCM聚类效果明显优于核主元熵FCM，聚类正确率提高了约21.1%。对于聚类个数事先未知的人工数据集，核主元熵FCM与FCM几乎不能实现有效聚类分析，聚类评价指标远远大于多核FCM，而多核FCM都得到了正确聚类个数，并且具有较小的聚类评价指标。由于多核FCM采用多重迭代确定最佳聚类个数，导致算法运算时间较长，可以采用线下并行计算的方式来提高运行效率。

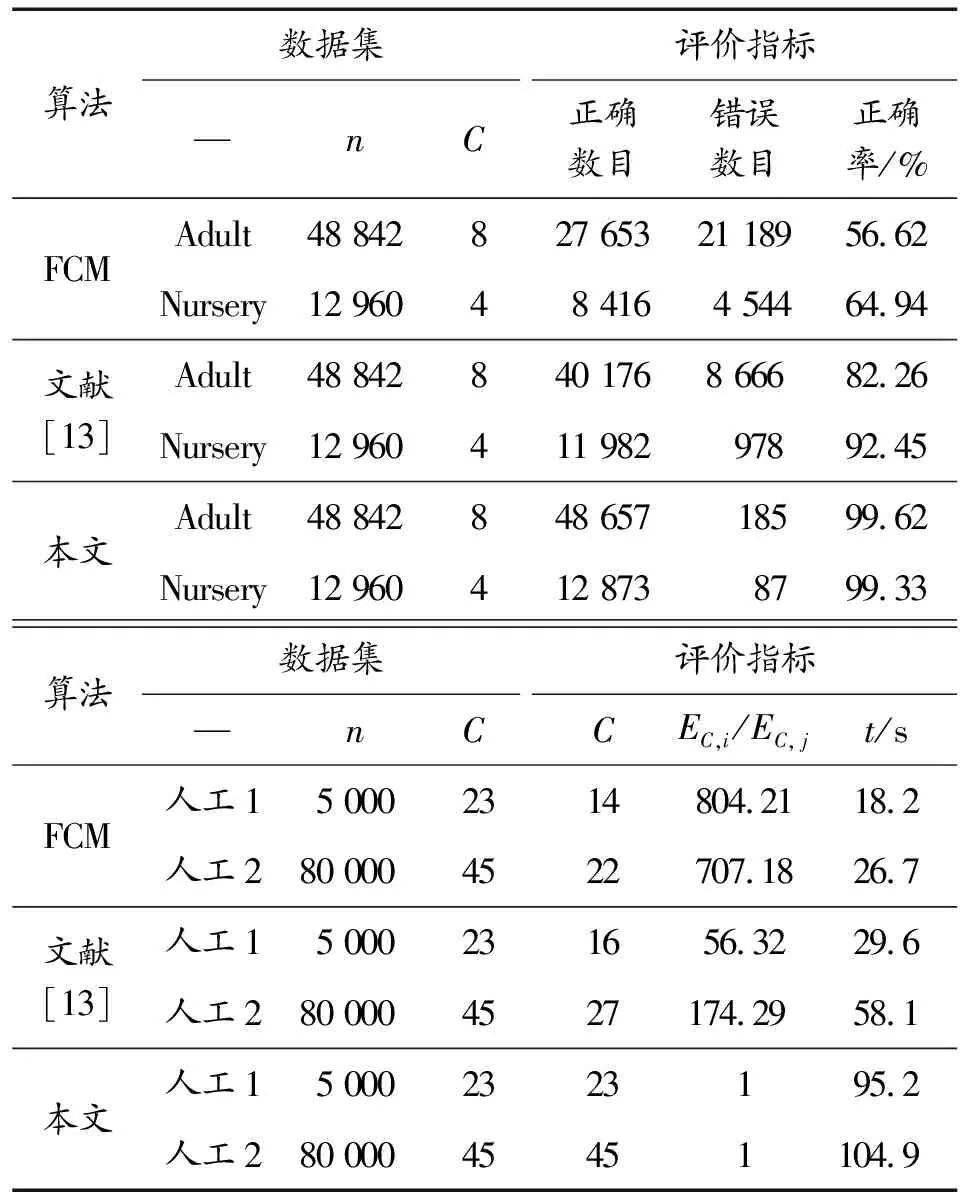
表3 评价指标对比

为了验证GOA算法收敛性能，选取WOA[16]、SCA[17]等新型智能优化算法对多核FCM迭代过程进行优化。图5、图6是在Nursery数据集和人工2数据集下J(U,V)收敛曲线。

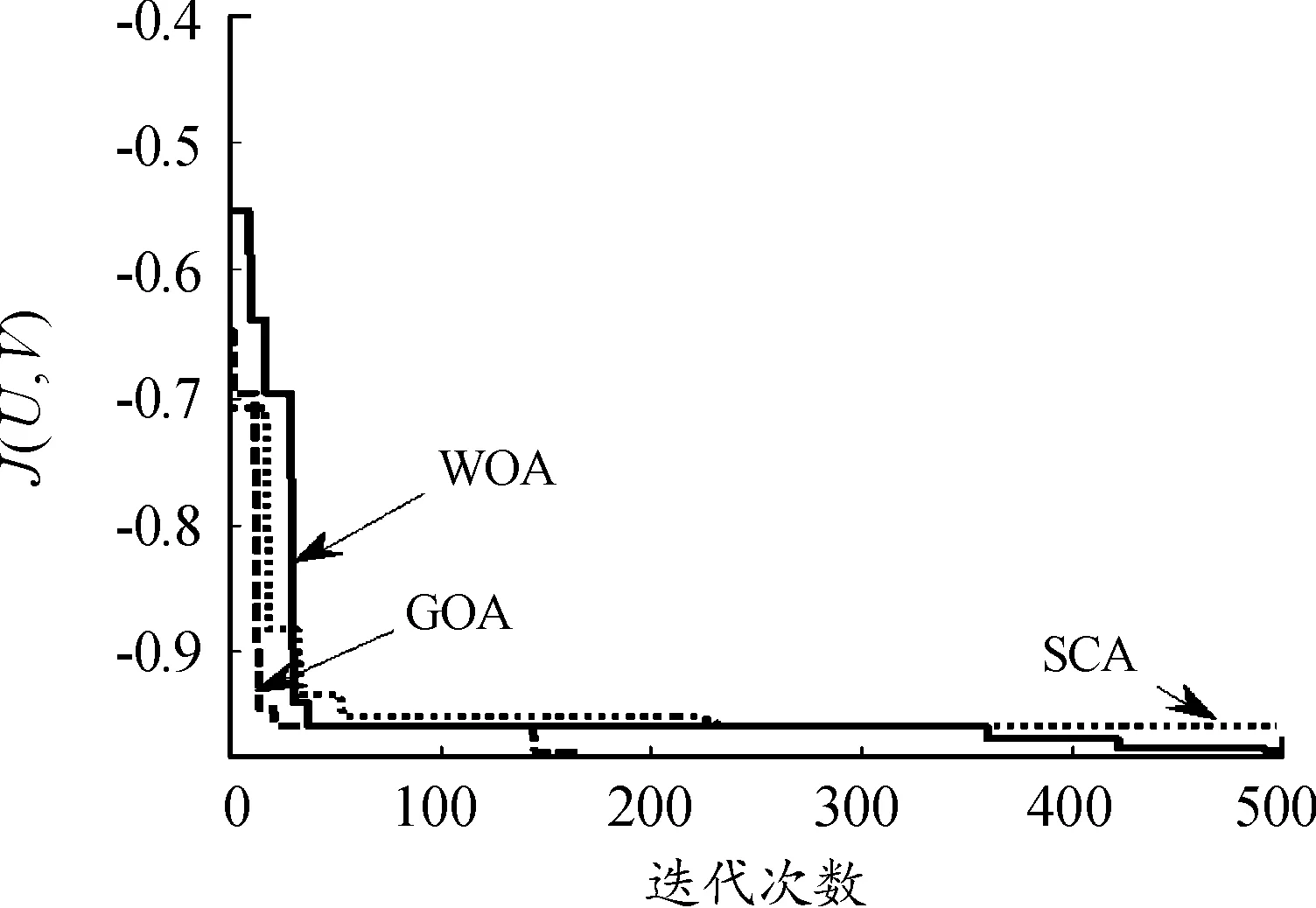
图5 Nursery数据集下收敛曲线

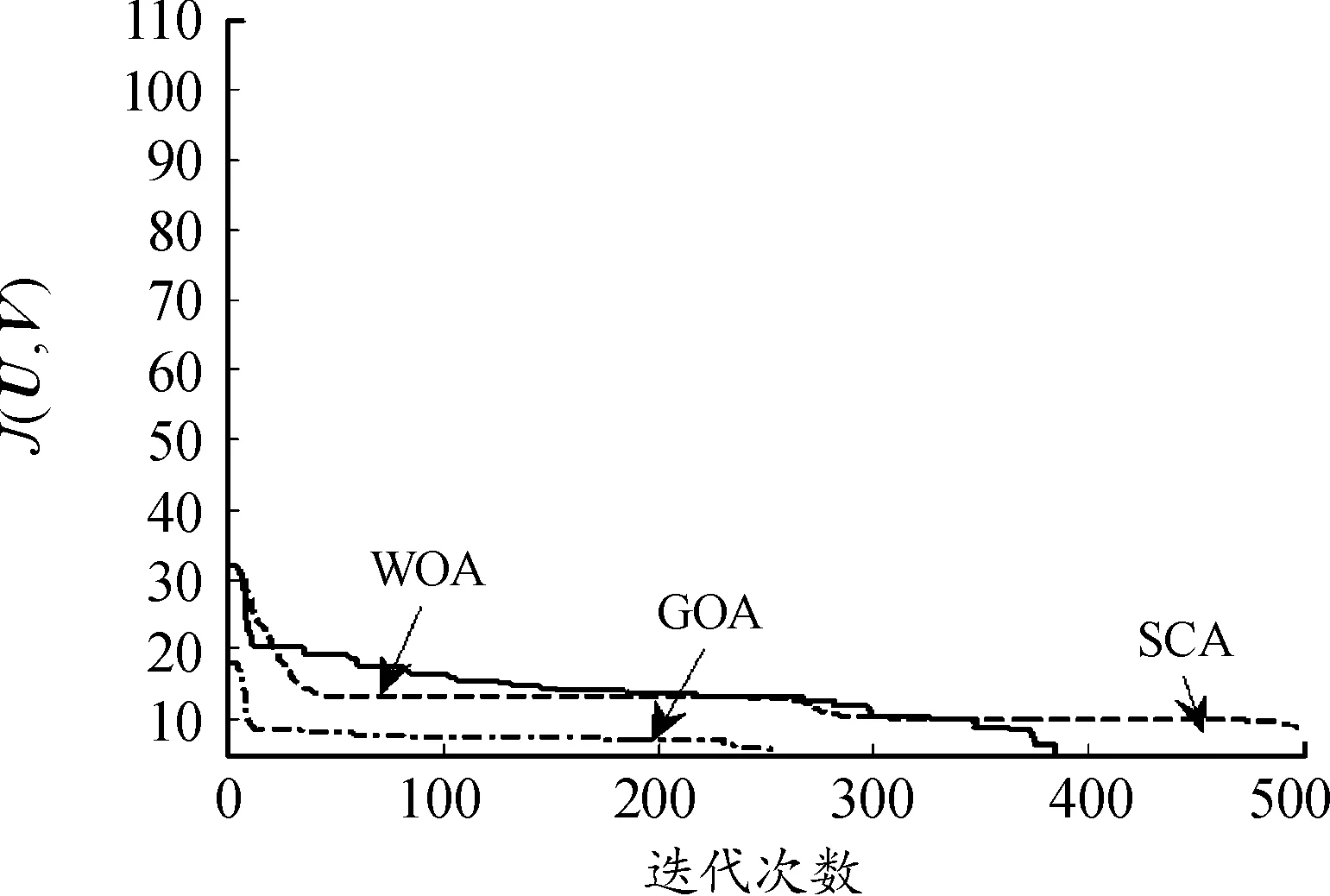
图6 人工2数据集下收敛曲线

从图5、图6可以看出：GOA具有较快的收敛速度和收敛精度，表明该算法具有较为突出的全局寻优能力。

4.2 多无人机协同侦查航迹规划

对多无人机协同侦查算例进行仿真(无人机、目标具体物理参数参考文献[2])。分别设置M=14、M=25，采用多核FCM对目标进行聚类分析，根据聚类个数派出无人机执行协同侦查任务，利用IDGOA给出航迹信息。IDGOA优化航迹规划阶段实质为多旅行商问题，为此采用文献[18]的改进分组遗传算法、文献[19-20]的新混合遗传算法进行对比实验。表4给出了实验结果，图7、图8给出了不同M值的IDGOA优化航迹结果。

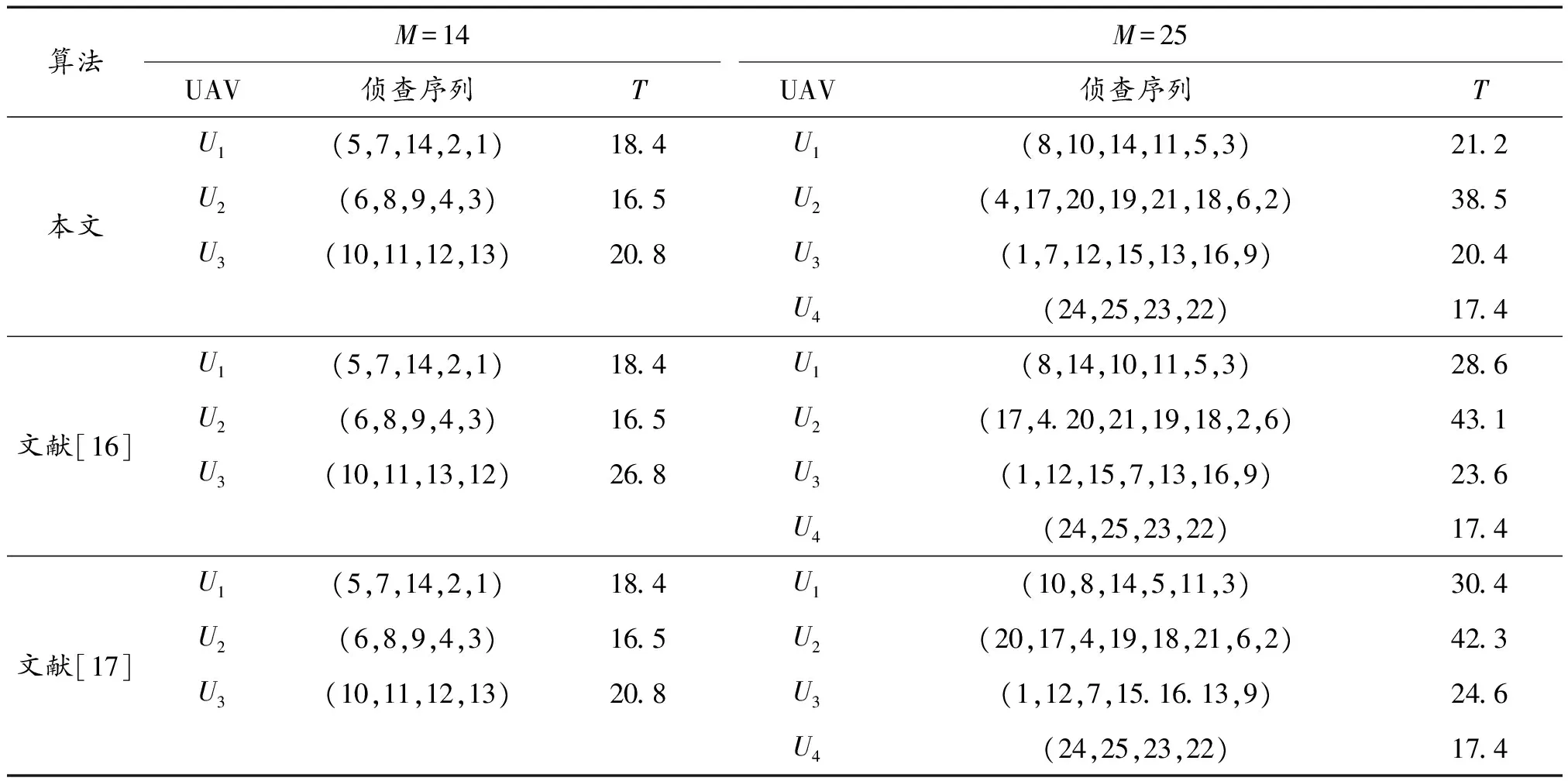
表4 实验结果

从表4可以看出：当M=14时，除文献[16]给出的U3侦查序列不同于其他2种算法外，其余具有相同的规划结果，这表明，对于小规模规划问题，3种算法几乎具有同样的规划能力。当M=25，3种算法仅仅对于U4给出了同样的侦查序列，而对于U1、U2、U3，IDGOA得到的整体任务时间明显优于其他2种算法，整体执行任务时间降低了约8.9%～10.7%，这表明，对于同样的航迹规划问题，IDGOA具有更加突出的全局寻优能力，收敛精度更高，这是因为自适应交换、自适应学习和突变3种更新策略的引入，进一步扩展了算法收敛空间，使得算法能够有效避免局部最优，进而得到更好地收敛结果。

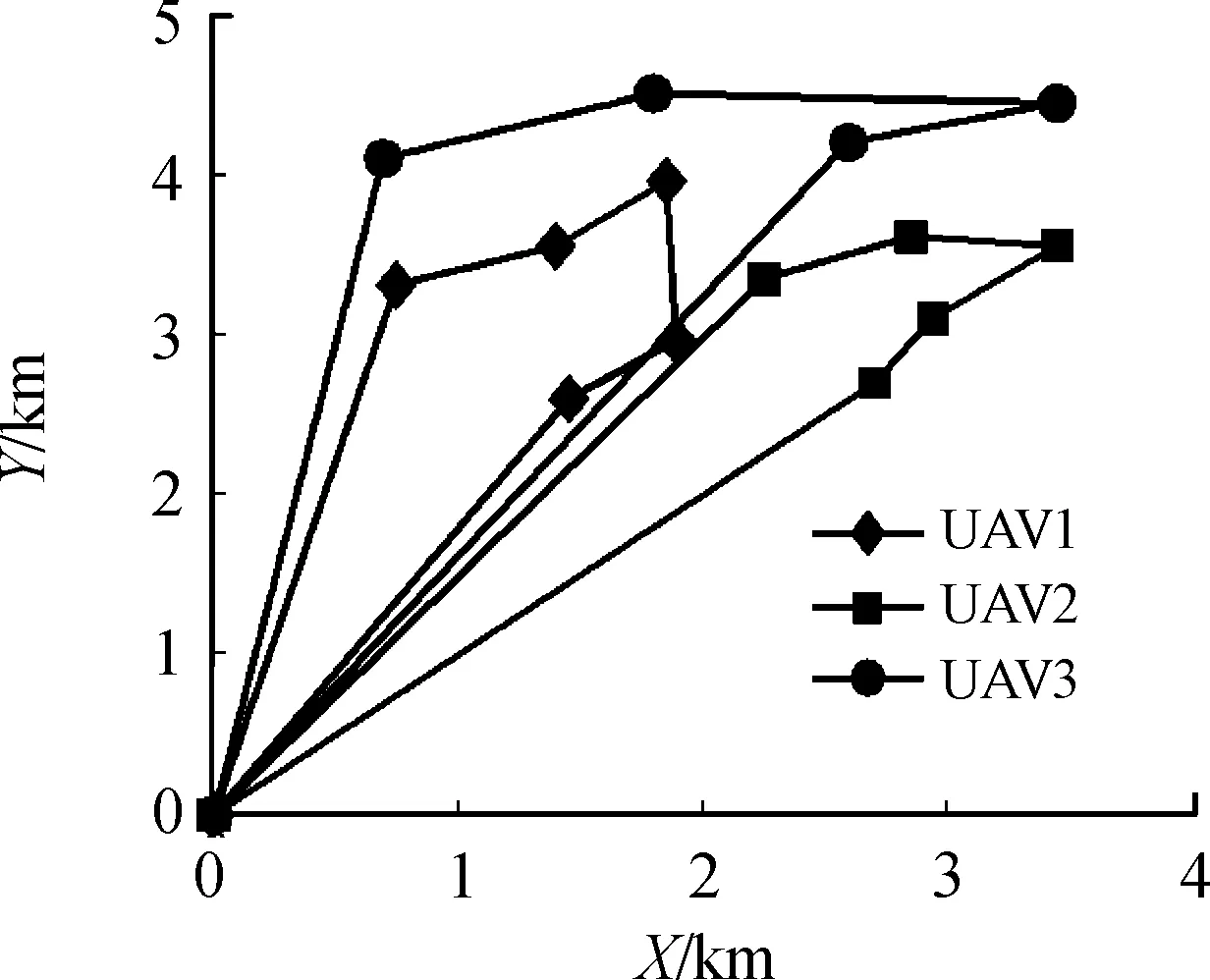
图7 M=14 IDGOA优化航迹Fig.7 The optimized track results for IDGOA with M=14

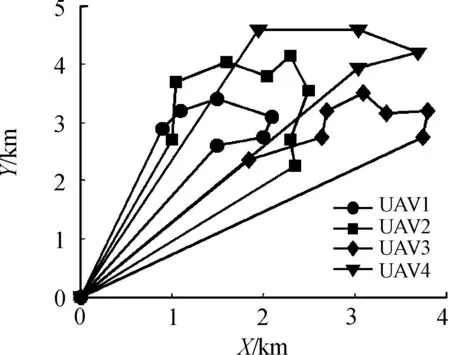
图8 M=25 IDGOA优化航迹

5 结论

针对多无人机协同侦察航迹规划问题，提出了一种联合多核FCM和GOA的多无人机协同侦查航迹规划算法。该算法将多核FCM引入到航迹规划中，通过对目标进行聚类分析，让具有更多相似属性的目标聚为一类，为多无人机协同决策提供了依据。而且，多核FCM稳定高效的聚类能力以及IDGOA复杂问题突出的优化性能，使得算法具有更好的航迹规划效率和更低的代价，仿真实验也分别证实了所提方法的有效性和优越性。