有效梳理 沟通联系 构建网络

冒金彬

一、参与整理，自主建构

师：这是我们学过的四种立体图形，你能说出它们的名称吗？（课件展示长方体、正方体、圆柱、圆锥）

师：我们习惯用这些字母表示它们的边线，你能说出这些字母分别表示什么吗？

师：课前大家已经根据自己的理解对这部分知识进行了整理（长方体、正方体从点、棱、面方面梳理，圆柱、圆锥从点、高、面方面梳理），请把你的成果在小组里交流，等会每组选派代表进行大组交流。

师：在整理的过程中，我们发现这些立体图形的特征都可以从“点、线、面”三个方面进行研究。

赏析：课前让学生先期梳理，适当温习，有助于调动学生的参与热情，促成知识的有效建构;课中有意识地鼓励学生开展小组讨论与大组展示，有助于帮助学生取长补短，厘清知识间的相互关系。在学生交流的基础之上，沈老师注重适时有效提升，在概括知识的同时，有效渗透方法指导。

二、有效思辨，自我反省

师：接下来我们来玩个游戏吧！老师这里有个袋子，袋子里装了一些立体图形，你能根据描述猜出摸到的是什么图形吗？

师：我摸到一个尖尖的顶点，不对，好像不是一个，它一共有8个顶点。我再摸一摸，有6个面，还有12条棱，相对的面完全相同。你能猜出是什么图形吗？为什么？

生1：有可能是长方体，也有可能是正方体。因为它们都具备这些特征。

师：我再摸一摸，它的12条棱，相对的棱长度相等，相对的两个面是完全一样的长方形。你现在猜是什么图形？为什么？

师：是呀，正方体具备长方体的所有特征，它是特殊的长方体。

师：再来猜一次，它有一个面是曲面。

生2：可能是圆柱体，也可能是圆锥体。

师：它还有两个底面，一个底面是圆形，另一个底面也是圆形。

生3：肯定是圆柱体。

师：一定是圆柱体吗？我们一起来看看，是圆柱体吗？（圆台）为什么不是圆柱体？

师：我们一起来看屏幕，其实这个立体图形是把圆柱的一个底面半径缩小一些得到的，如果把它的这个底面半径继续缩小，直到缩小到圆心这个点，这个立体图形就会成为一个圆锥。

赏析：为帮助学生厘清这几个图形间的联系，沈老师精心设计了猜图形的游戏。通过教师的描述和对关键点的提取，学生在思辨中加深了对图形的理解，而对圆柱、圆台与圆锥的动态演绎，也让学生知道立体图形还有很多，它们之间是密切关联的，而我们现在学习的仅仅是其中的一部分。游戏的设计不仅能调动学生的参与热情，还能激发学生的探究意识，也为下面的复习作好铺垫。

三、展开联想，整体感知

师：在组成立体图形的点、线、面中，面与立体图形的联系是最为紧密的。让我们看这个长方体展开图（图1）的前面、下面和左面，你会试着在作业纸上画出展开图的另外三个面吗？

师：长方体的展开图都是由3对长方形组成的，每对长方形的大小完全相同。其中同样大小的两个长方形中间一定只隔一个其他的长方形。如果是正方体，你能很快判断出哪些是正方体的展开图吗？说说理由。（如图2）

师：如果把这些正方体的展开图分一分类的话，我们可以分为哪几类？（四类，141、231、222和33）

师：根据展开图每行小正方形的个数，我们可以分为这样的四类。掌握了这些规律，就能帮助我们快速判断是否可以围成正方体了。

师：如果把圆柱的表面展开又是什么图形呢？侧面展开后的长方形的长与宽分别和圆柱有什么关系呢？

赏析：在研究立体图形表面的展开与合围时，沈老师没有停留在简单的画一画、说一说上，而是引导学生总结规律，教会学生方法，这样学生就学而不感其难了。在教学中有意突出情况相对复杂的正方体，通过分类与思辨，梳理出四类特殊情况，并赋予易记的名字，从而使难点不再困难。

四、引发想象，感悟联系

1. 复习三视图，鼓励思辨。

师：其实研究立体图形的面，我们还可以研究它的视图。我们在观察立体图形时，从不同的角度能看到它不同的面，有时能看到一个或两个面，最多可以看到三个面。

师：说说看，我们从长方体和正方体的正面、侧面与上面看到的分别是什么图形。

说一说：

（1）一个立体图形由5个同样大小的小正方体拼成（图3），如果要再放一个这样的小正方体，而且要求上面和侧面看到的图形不变，应该放在哪里呢？

（2）一个用小正方体拼成的大长方体，从正面和上面看到的图形分别如图4。想一想，从右面看，看到的是（  ）号图形。

师：看课件演示，你选择对了吗？看来用小正方体拼摆成长方体，根据两个面看到的图形，我们就能确定是一个怎样的长方体了。

师：长方体和正方体的三视图都是长方形或者正方形。那圆柱和圆锥呢？说说看。

2. 复习剖面图，引发想象。

师：圆锥从正面和侧面看到的是一个等腰三角形，圆柱从正面和侧面看都是一个长方形，其实这两个图形也可以看成是圆锥体和圆柱体的截面。

师：看着这两个平面图形，你还能想象出原来的圆柱和圆锥吗？将等腰三角形绕着对称轴旋转一周就得到了这个圆锥，将长方形绕着中间的对称轴旋转一周就能得到这个圆柱，看来这两个平面图形还和旋转有关。如果老师只给出这些平面图形的一半，你还能想象出原来的圆柱和圆锥吗？先看一看，再闭上眼睛想一想。

师：这样一个直角三角形绕着长直角边旋轉一周还是能得到刚才的圆锥，那么这个直角三角形的这条直角边就是圆锥的什么呢？另一条直角边就是圆锥的什么呢？

师：同样的小长方形绕它的长边旋转一周就能得到一个圆柱体。这个小长方形的长、宽与这个圆柱有什么关系？

师：下面老师来考考大家。一个立体图形，从正面看是一个正方形，这个立体图形可能是什么图形？

师：（课件动态演示）正方形往后平移，它的运动轨迹就是一个长方体或者正方体。圆形平移得到圆柱，平移到一定的高度，从正面看到的会是一个正方形，这时的底面直径和高相等。也就是说，这个立体图形可能是长方体、正方体或圆柱体，那么再添加什么条件，这个图形就肯定是圆柱体？

师：把一些平面图形通过旋转可以得到立体图形，借助平移也能得到立体图形。

练一练：（先呈现基本图形，再根据学生描述动态呈现切割图形，然后计算）

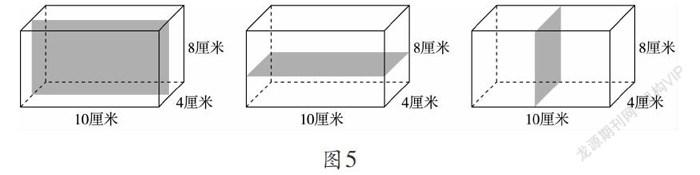
（1）把长方体（图5）切割成两个完全一样的小长方体，表面积最多增加多少？最少呢？

（2）把圆柱（图6）切割成完全一样的两部分，表面积最多增加多少？最少呢？

（3）把圆锥（图7）切割成完全一样的两部分，表面积增加多少？

赏析：从不同的角度沟通立体图形与平面图形的联系，从“视图”的角度沟通联系，引导学生进一步感悟“面在体上”;利用闭目合理想象，加上“点动成线，线动成面，面动成体”的多媒体演示，帮助学生实现平面图形与立体图形的有效关联。

（作者单位：江苏省如东县教师发展中心 责任编辑：王彬）